最大似然估计

在经济学和统计学的世界里，我们经常面临这样一个问题：如何从有限的数据中推断出真实的经济规律？这就像是一位侦探通过有限的线索来推断案件真相一样。假如你只拥有一部分数据线索，就需要找到能最合理解释这些数据背后规律的方法。

最大似然估计正是解决这个问题的强大工具。它的核心思想是：我们已经观测到数据了，那么哪些参数值最有可能“生成”这些观测到的数据？最大似然估计的方法就是，设法找出一组参数，使得在这些参数下，能够观测到已有数据的概率最大。比如说，无论是分析经济增长、预测股票市场，还是估计消费者偏好，我们都可以利用最大似然估计去推断最符合实际的数据生成机制。

总之，在实际分析中，最大似然估计帮助我们从观察到的数据中系统、科学地找到最可能的参数值，让我们在不确定性中也能做出尽量接近真实的判断。

什么是最大似然估计

假如你是一家电商平台的数据分析师，你观察到每天的订单数量，想要推断出用户购买行为的规律。面对这样的问题，我们需要一种可以“反推”出数据背后规律的方法。最大似然估计（Maximum Likelihood Estimation, MLE）正是统计学中常用且强大的参数估计工具。它的核心思想，就是找到能够让我们实际观测到这组数据的“概率”最高的参数值。

最大似然估计的核心思想是：既然这些数据已经发生了，那么使这些数据出现概率最大的参数值，很可能就是真实的参数值。

在实际应用中，这一思想方法非常灵活。比如说，如果你观察到某个商品在过去10天的销售量分别是：15、18、20、17、19、21、16、22、18、20件，那么你自然想知道，这个商品每天的平均销售量大约是多少？以及用户购买的变动性有多大？最大似然估计会用一套严谨的数学方法，帮你找到一组参数（如均值和方差）的估计值，让“在这些参数条件下，观测到刚才那组销售数据的概率”达到最大。

从这个图表可以看出，销售量在15-22件之间波动，平均值约为18.6件。最大似然估计会找到最能解释这种波动模式的参数值。

进一步说，最大似然估计并不仅仅用于估计均值。比如在金融领域，如果我们想分析股票收益率的分布参数、判断某项风险的发生率，甚至在医疗、工程等领域分析故障率、转化率等，都可以用MLE来估计相关参数。它可以用于各种各样的概率模型，比如二项分布、正态分布、泊松分布等。

最大似然估计的魅力还在于它为后续的统计推断（如参数置信区间、假设检验）和模型比较打下坚实基础。理解最大似然估计，是掌握现代统计建模的第一步。

---

似然函数的本质

从概率到似然的转换

在日常生活中，我们经常从参数已知的情况下去计算某个事件的概率。例如，已知一个骰子是公平的（即每个面出现的概率都是 $1/6$），那么投掷一次出现6点的概率是多少？这类问题属于“已知参数，求样本”的正向推断。而在经济分析和数据科学实践中，我们面临的却常常是逆向的问题：我们观察到了结果（例如某只股票连续5天上涨），却不知道背后的参数（比如这只股票真实的上涨概率 $p$），需要反推出参数的可能值。

在这种场景下，我们就将研究的视角从“概率函数”转变为“似然函数”。用数学语言表述：对于随机变量 $y$，如果在参数 $\theta$ 已知时，其概率密度函数为 $f(y|\theta)$。假设我们观测到了 $n$ 个独立的数据点 $y_1, y_2, \ldots, y_n$，则其联合密度函数为：

$$f(y_1, y_2, \ldots, y_n \mid \theta) = \prod_{i=1}^{n} f(y_i \mid \theta)$$

我们将其作为参数 $\theta$ 的函数来考察，记为似然函数：

$$L(\theta \mid y) = \prod_{i=1}^{n} f(y_i \mid \theta)$$

这里，$L(\theta \mid y)$ 表示在参数 $\theta$ 给定的情况下，观察到样本 $y=(y_1, y_2, ..., y_n)$ 的“可能性大小”（不是概率，专指针对本样本相对参数的不同比较）。的本质，就是寻找使 达到最大的那个 值。

直观例子

为了更直观理解似然函数，假设我们有一组观测数据，希望估计其均值参数。如下图展示了参数值与似然函数之间的关系：

从图表可以看到，当参数值为 $18.6$ 左右时，似然函数 $L(\theta\mid y)$ 达到峰值。这恰恰是最大似然估计给出的最有可能的参数值。函数的形状显示不同参数值“产出”当前这组样本的相对可能性。

若我们改变数据，似然函数的峰值和形状也会发生变化。这样，似然函数将“数据和参数的关系”用定量的方式表达了出来，是推断真实参数的桥梁。

对数似然函数的优势

在实际的统计推断和模型估计中，我们几乎总是使用对数似然函数（log-likelihood），即对似然函数取自然对数：

$$\ln L(\theta \mid y) = \sum_{i=1}^{n} \ln f(y_i \mid \theta)$$

使用对数变换有几个关键优势：

1. 计算简化：原本的连乘积计算通过对数变成了求和，使得数学推导和程序实现都大大简化。这类似于在计算复合利率或累积分数时，采用对数操作可以转换复杂的连乘关系为简单的加法。

2. 数值稳定性增强：当样本量很大时，若直接计算多个概率密度的乘积，结果很容易下溢为0（即超出计算机能表示的最小数），而对数转换可以保持数值在可计算范围内，提高了数值运算的稳定性。

3. 便于求导与参数优化：许多优化算法（如牛顿法）都要求目标函数可微可导，而对数似然函数通常具有良好的数学性质，便于分析最大值的解。

总之，对数似然是最大似然估计实际应用时必不可少的工具。

---

参数识别问题

在应用最大似然估计前，必须首先确保参数是可识别的。所谓“参数可识别”，是指不同的参数取值 $\theta_1 \neq \theta_2$ 能导致不同的似然函数取值，即：

$$L(\theta_1 \mid y) \neq L(\theta_2 \mid y)$$

这意味着通过观察到的数据 $y$，不同的参数值 $\theta$ 可以被正确区分，否则我们就无法利用数据推断参数的真实取值。

经济学中的识别问题

考虑一个简单的线性回归模型：

$$\text{收入} = \beta_1 + \beta_2 \times \text{教育年限} + \varepsilon$$

如果你的观测数据中，所有人的教育年限都完全相同，即 $\text{Var}(\text{教育年限}) = 0$，那么任何 $\beta_2$ 都会导致同样的似然函数值。此时，$\beta_2$ 无法识别，因为收入的变化与教育年限的变化在数据中没有体现。类似地，这就像试图通过一条完全水平的直线去推断其斜率——这样的斜率是无法确定的。

在经济学与实际统计建模中，识别性是理论与实证分析的前提。从而在数据获取与实验设计阶段，要特别关注参数的可识别性。

---

最大似然估计的优良性质

最大似然估计之所以广泛应用于经济学与统计推断，是因为它具备一系列极其重要的统计性质，为科学决策和有效建模提供了可靠依据。

一致性（Consistency）

最大似然估计量具有一致性，即随着样本容量 $n \rightarrow \infty$，MLE $\hat\theta$ 将以概率收敛于真实参数值 $\theta_0$。用公式表达即：

$$\hat{\theta}_n \xrightarrow{p} \theta_0 \quad (n\to\infty)$$

就像投掷硬币次数越来越多，观测到正面的频率逐渐收敛于真实概率 0.5。

如上图所示，随着样本容量 $n$ 增加，$\hat\theta$ 到真实 $\theta_0$ 的误差迅速减小。这一性质对经济学建模极为关键，说明只要数据充分，MLE 给出的参数估计就会非常接近真实世界的规律。

渐近正态性（Asymptotic Normality）

在样本量充分大时，最大似然估计量 $\hat\theta$ 近似服从下列正态分布：

$$\hat{\theta} \sim N\Big(\theta_0,\; \big\{I(\theta_0)\big\}^{-1}\Big)$$

其中，$I(\theta_0)$ 为参数 $\theta$ 的信息矩阵，定义为对数似然函数的二阶导数的负期望，

$$I(\theta) = -\mathrm{E} \left[ \frac{\partial^2 \ln L(\theta \mid y)}{\partial \theta^2} \right]$$

此性质意味着，我们可以利用正态假设进行以下分析：

• 构建置信区间：推导参数估计的置信区间
• 假设检验：进行假设检验，检验参数是否等于某个特定值
• 模型比较：比较不同经济模型的拟合优劣

渐近有效性（Asymptotic Efficiency）

最大似然估计量还具备极佳的“有效性”，即在所有一致且渐近正态的估计量类中，MLE 达到了最小的渐近方差。用数学表达即：

$$\mathrm{Var}(\hat{\theta}) \to \big\{I(\theta_0)\big\}^{-1}$$

这一性质说明，大样本下，没有其他估计器比MLE“更精确”或使估计值的分布更集中。

不变性（Invariance）

最大似然估计具有不变性，如果 $\hat{\theta}$ 是参数 $\theta$ 的最大似然估计，那么对于任意连续可微函数 $c(\theta)$，其最大似然估计为 $c(\hat{\theta})$。公式如下：

$$\text{如果}~ \hat{\theta} = \arg\max_\theta L(\theta \mid y)，~~\text{则}~ \widehat{c(\theta)} = c(\hat{\theta})$$

这个性质在应用中非常方便。例如，如果我们用MLE估计出了 $\sigma^2$（某变量的方差），那么 $\sigma$（标准差）的最大似然估计自然就是 $\sqrt{\hat{\sigma}^2}$，无需额外推导或重新估计。

此外，任何参数的单调变换、函数变换的最大似然估计，都可由原参估计带入后得到。

---

信息矩阵的经济学含义

信息矩阵（Fisher Information Matrix）不仅是统计学中的基础工具，它在经济学的建模、推断和决策过程中也具有极其重要的意义。可以简单理解为：信息矩阵衡量了我们的数据中，关于待估参数“包含了多少信息”。信息量越大，我们对参数的估计就越精确，方差越小。

例如，在对同一个经济现象建模时，如果某组数据的信息矩阵更“大”（正定矩阵意义下），它能让我们对参数的不确定性降低、更接近真实世界。因此，信息矩阵既是统计效率的度量，也是模型可识别性的“体检表”。

信息矩阵等式

在最大似然估计理论中，有一个非常重要且优美的结论——信息矩阵等式（Information Matrix Equality）：

$$\operatorname{Var}\Bigg(\frac{\partial \ln L(\theta \mid y)}{\partial\theta}\Bigg) = -\mathrm{E}\Bigg(\frac{\partial^2 \ln L(\theta \mid y)}{\partial\theta^2}\Bigg) = I(\theta)$$

也就是说，似然函数一阶导数（得分函数，score）的方差，等于对数似然函数二阶导（的负期望值），并且都等于信息矩阵本身。这个等式不是巧合，而是深刻反映了极大似然理论的内在对称性：信息矩阵既可以通过一阶导数的变异性来衡量，也可以通过二阶导曲率来理解。

实际应用中的信息矩阵

在经济学的实证和理论分析中，信息矩阵被广泛应用于以下几个核心环节：

• 评估估计精度：参数估计的不确定性（渐近方差）由信息矩阵的逆矩阵给出。例如对政策效应的置信区间、经济波动参数的显著性检验等，都依赖信息矩阵度量估计的可信度。信息矩阵越大、精度越高，参数区间越窄。

• 实验与数据设计：在设计实验或搜集样本时，经济学家常常优化信息矩阵（如最大化行列式或迹），以便提高估计的效率。这涉及实验设计理论中的最优设计（Optimal Design），比如A-optimal、D-optimal等策略。

• 模型检验与比较：在比较两个经济模型的信息含量时，可以利用信息矩阵（或其迹、特征值）衡量哪个模型对参数的识别能力更强、更容易区分理论假设。例如在选择不同的投资回报率函数、消费者行为模型时，这类分析能指导模型选择。

• 识别与参数可辨性：如果信息矩阵不是满秩，那么参数可能无法被唯一识别。这个现象在结构性计量模型、复杂宏观经济模型中很常见，信息矩阵提供了识别性的数学判断依据。

---

正态分布下的最大似然估计

我们通过一个例子详细体会最大似然估计（MLE, Maximum Likelihood Estimation）从模型假设到计算的全部过程。假设我们获得了一组来自正态分布的独立同分布样本 $y_1, y_2, \ldots, y_n$，设其总体均值为 $\mu$，方差为 。

对数似然函数

此时，样本的联合概率密度函数为：

$$f(y_1, \ldots, y_n \mid \mu, \sigma^2) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(y_i - \mu)^2}{2\sigma^2} \right)$$

将上式取自然对数，得到正态分布下的对数似然函数（省略与参数无关的常数性质）：

$$\ln L(\mu, \sigma^2 \mid y) = -\frac{n}{2} \ln(2\pi) - \frac{n}{2}\ln\sigma^2 - \frac{1}{2\sigma^2} \sum_{i=1}^n (y_i - \mu)^2$$

这个对数似然函数包含三部分：一是常数项 $-\frac{n}{2}\ln(2\pi)$，二是方差对数项 $-\frac{n}{2}\ln\sigma^2$，三是偏差平方和项 。

求解最大似然估计

对 $\mu$ 和 $\sigma^2$ 这两个参数分别对 $\ln L$ 求偏导，并令导数为零，可以解出最大似然估计。

对 $\mu$ 求偏导并令为零可得：

$$\frac{\partial \ln L}{\partial \mu} = \frac{1}{\sigma^2}\sum_{i=1}^n (y_i - \mu) = 0 \implies \widehat{\mu}_{\mathrm{MLE}} = \frac{1}{n} \sum_{i=1}^n y_i$$

对 $\sigma^2$ 求偏导并令为零可得：

$$\frac{\partial \ln L}{\partial \sigma^2} = -\frac{n}{2\sigma^2} + \frac{1}{2(\sigma^2)^2} \sum_{i=1}^n (y_i - \mu)^2 = 0$$

代入 $\widehat{\mu}_{\mathrm{MLE}}$，解得最大似然估计量：

$$\widehat{\sigma}^2_{\mathrm{MLE}} = \frac{1}{n} \sum_{i=1}^n (y_i - \overline{y})^2$$

其中 $\overline{y}$ 为样本均值。

也就是说，均值的最大似然估计就是样本均值，方差的最大似然估计是“除以 $n$” 的样本方差。

经济学解释与注意点

上述结果告诉我们，在正态分布假设下，样本均值即为总体均值 $\mu$ 的最大似然估计，这与直观和其他统计方法是一致的。但需要注意的是，$\sigma^2$ 的MLE为

$$\widehat{\sigma}^2_{\mathrm{MLE}} = \frac{1}{n} \sum_{i=1}^n (y_i - \overline{y})^2$$

即分母为 $n$，而经典“无偏”样本方差的分母通常是 $n-1$。当样本容量 $n$ 较小时，这会带来一定的偏差。

---

基于最大似然的假设检验详解

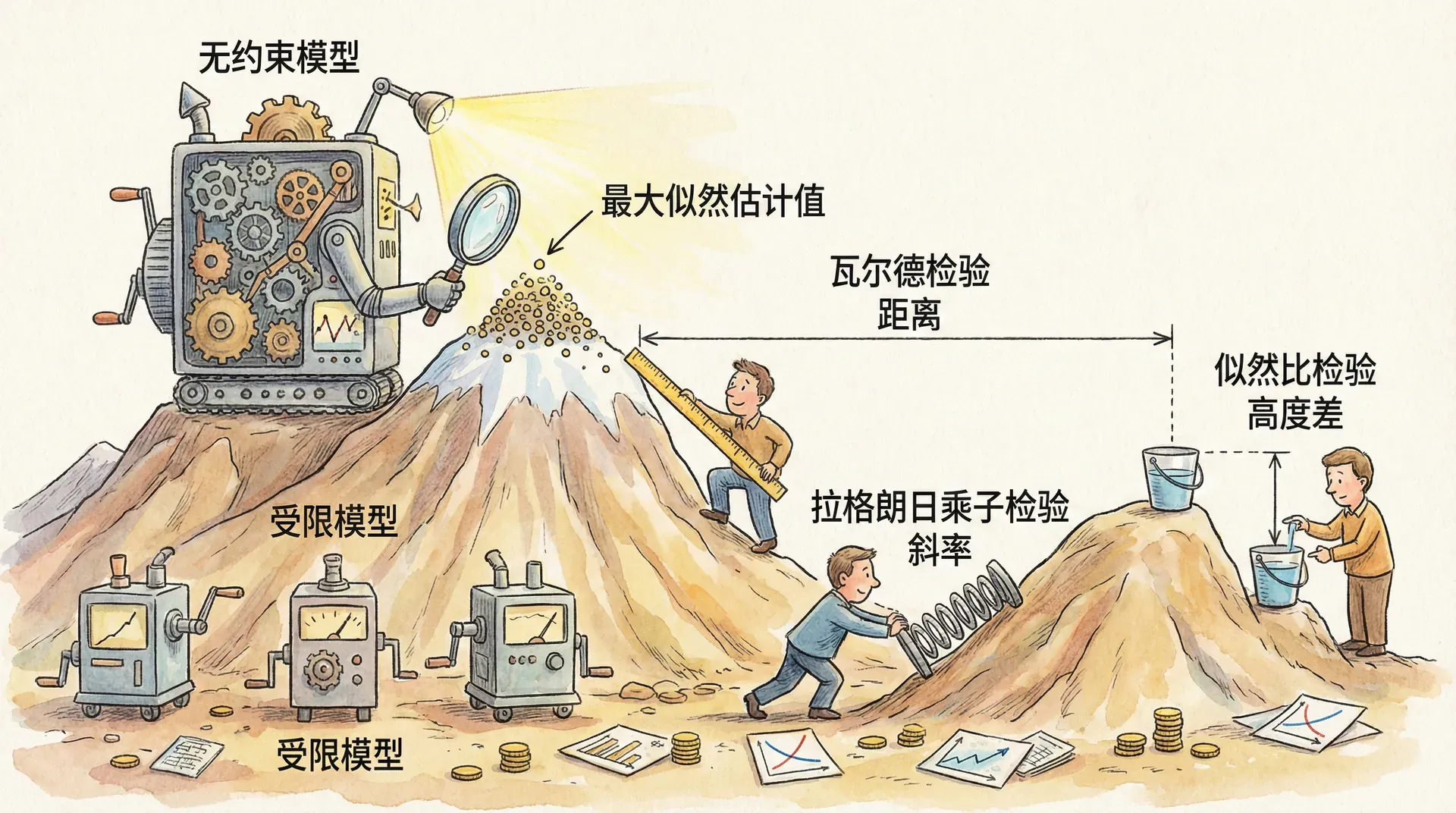
最大似然估计不仅为参数提供了估计值，还构建了一套功能强大的假设检验体系，包括似然比检验（Likelihood Ratio Test）、沃尔德检验（Wald Test）、拉格朗日乘数检验（Lagrange Multiplier Test，简称LM检验）。这些方法广泛应用于经济学各类理论假设的实证验证。

似然比检验（Likelihood Ratio Test, LR）

似然比检验是最大似然理论下最常用的检验方法。基本思想是比较受约束（原假设 $H_0$）与非受约束模型（备择假设 $H_1$）的最大对数似然值。 检验统计量定义为：

$$LR = -2\left[\ln L_R - \ln L_U\right]$$

其中 $L_R$ 表示受约束模型下的最大似然值，$L_U$ 表示非受约束模型最大似然值。对于常见的正态线性模型，$LR$ 在 $H_0$ 成立时渐近服从 分布，自由度为所加约束的数量。

实际经济学例子：例如，假设我们检验教育与经验对工资的边际效应是否相等。可构建如下两个模型：

• 受约束模型: $工资 = \beta_0 + \beta_1(\text{教育} + \text{经验}) + \varepsilon$
• 非受约束模型: $$

分别计算两个模型的最大对数似然，应用上述 $LR$ 正式完成检验。

沃尔德检验（Wald Test）

沃尔德检验直接基于参数估计及其渐近方差矩阵，检验参数约束 $H_0: c(\theta)=0$ 是否成立。 其检验统计量为：

$$W = \left[ c(\hat{\theta}) \right]^T \left[ \operatorname{Asy.Var}\left( c(\hat{\theta}) \right) \right]^{-1} \left[ c(\hat{\theta}) \right]$$

只需对非受约束模型做估计即可，尤其适合参数显著性检验（如检验 $\beta=0$ 对应系数是否显著）。

拉格朗日乘数检验（Lagrange Multiplier Test, LM）

拉格朗日乘数检验基于受约束模型下似然函数关于参数的梯度（得分），检验在约束成立时梯度是否接近零。只需对受约束模型做一次估计。线性模型下LM检验也称Score检验。

三种检验方法要点对比小结：

三种检验方法在大样本下均等价，实践中常根据应用场景及计算便利性灵活选择。

---

经济学中的实际应用

最大似然估计（MLE）不仅是理论方法，更在实际经济研究的多个领域里扮演着举足轻重的角色。下文通过具体经典模型和公式，介绍MLE在三类经济学问题中的应用场景。

消费者需求分析

在消费者需求分析中，最常见的是对需求函数参数的估计。比如我们可以考虑如下对数线性需求模型：

$$\ln Q_i = \beta_0 + \beta_1 \ln P_i + \beta_2 \ln I_i + \varepsilon_i$$

其中，$Q_i$ 表示第 $i$ 个消费者（或市场）的需求量，$P_i$ 为价格，$I_i$ 是收入， 分别为截距项与弹性系数， 是误差项。通常假设 。

在最大似然方法下，我们建立观测数据似然函数：

$$L(\beta_0, \beta_1, \beta_2, \sigma^2 \mid \mathbf{y}, \mathbf{P}, \mathbf{I}) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{1}{2\sigma^2} (\ln Q_i - \beta_0 - \beta_1 \ln P_i - \beta_2 \ln I_i)^2\right)$$

取对数求最大值得到参数估计。

参数 $\beta_1$ 称为价格弹性，衡量 $\ln P$ 对 $\ln Q$ 的影响；$\beta_2$ 为收入弹性。弹性值的经济意义如下：

• 若 $\beta_1 < 0$，则价格升高需求降低，满足需求定律；
• 若 $|\beta_1| > 1$，表明需求对于价格高度敏感（富有弹性）。

让我们用一组假设性数据绘制需求曲线，并标出具体弹性：

如图，价格上升（$P$ 增大）时，需求量（$Q$）下降，表现出了负的需求弹性。最大似然方法不仅可以估计回归系数，还允许推断弹性和其置信区间，从而支持经济政策分析和市场报告。

金融市场波动性建模

在金融领域，资产收益的波动性建模尤为重要。最经典的模型为 GARCH（广义自回归条件异方差）：

$$r_t = \mu + \varepsilon_t$$ $$\varepsilon_t = \sigma_t z_t$$ $$\sigma_t^2 = \alpha_0 + \alpha_1 \varepsilon_{t-1}^2 + \beta_1 \sigma_{t-1}^2$$

其中 $z_t \sim N(0, 1)$，$r_t$ 是资产收益，$\sigma_t^2$ 为条件方差。假定收益的分布已知，可以直接构造似然函数，采用MLE估计 等参数。

GARCH 的最大似然函数为：

$$L(\theta) = \prod_{t=1}^T \frac{1}{\sqrt{2\pi\sigma_t^2}} \exp\left(-\frac{(r_t - \mu)^2}{2\sigma_t^2}\right)$$

最大似然估计能有效捕捉波动性的“聚集效应”，即高波动时期往往紧跟高波动。

图中波动性的“集群”为金融风险管理提供重要依据。实际估计中，MLE方法可以推广到多种误差分布（如$t$ 分布），以适应金融数据的厚尾特征。

劳动经济学中的工资决定与样本选择校正

在劳动经济领域，工资函数经常受到样本选择偏差困扰（如只观测到就业者工资）。Heckman两步法和MLE可用于解决此问题。一般建模如下：

选择方程：

$$\text{就业}_i^* = \mathbf{Z}_i^T \gamma + u_i \\ \text{若 } \text{就业}_i^* > 0, \text{则可观测到工资}$$

工资方程（仅对已就业者）：

$$\ln(\text{工资}_i) = \mathbf{X}_i^T \beta + \varepsilon_i$$

其中，$(u_i, \varepsilon_i)$ 通常设为联合正态分布。最大似然方法通过对联合分布的完全建模，联合估计 $\gamma,\ \beta$ 等参数，有效修正样本选择带来的偏误，使工资方程的系数更可信赖。

如果观测不到未就业者工资，只估计已就业者的数据，将使 $\beta$ 的估计结果出现偏差，而MLE校正后可得一致的参数估计。

---

计算方法和数值优化

最大似然估计求解通常涉及非线性优化，常用方法包括牛顿-拉夫逊法、评分（Fisher Scoring）方法等，并借助现代统计软件实现高效计算。

牛顿-拉夫逊方法

牛顿-拉夫逊方法（Newton-Raphson）通过迭代方式寻找参数的极大似然解，其迭代更新公式为：

$$\theta^{(k+1)} = \theta^{(k)} - [H(\theta^{(k)})]^{-1} g(\theta^{(k)})$$

其中，$g(\theta)$ 表示目标函数对参数的梯度（得分向量），$H(\theta)$ 为目标函数的 Hessian 矩阵。

由图可见，参数经过有限次数迭代后迅速收敛到真实值，说明牛顿-拉夫逊法在最大似然估计中的高效性。需要注意的是，Hessian矩阵的正定性和数值稳定性对算法收敛性有重要影响。

评分方法（Fisher Scoring）

评分方法用信息矩阵 $\mathcal{I}(\theta)$（得分函数的协方差）代替Hessian矩阵，迭代更新为：

$$\theta^{(k+1)} = \theta^{(k)} + [\mathcal{I}(\theta^{(k)})]^{-1} g(\theta^{(k)})$$

在GLM等模型中，信息矩阵的形式简单、数值性质好，因此评分方法常被采用，收敛过程更加平稳。

现代计算工具

得益于现代统计计算发展，无论多复杂的最大似然问题都可以通过主流软件快速实现：

• R语言：可使用 optim()、nlm() 等通用优化器，或专业包如 maxLik、TMB
• Python：常用 scipy.optimize，亦可用 statsmodels 或 PyMC 等
• Stata：有一整套 ml 命令支持用户自定义似然函数
• EViews：提供图形界面操作最大似然估计与广义线性建模

这些工具大幅降低了MLE在现实经济分析中的实施门槛。

---

总结

最大似然估计是现代经济学研究中不可替代的重要工具，它为参数估计提供了高效的方法论，也为假设检验和模型比较建立了统一的框架。其核心思想在于，通过寻找最有可能生成观测数据的参数值，让模型参数与实际数据之间实现最佳契合。最大似然估计不仅具备一致性、渐近正态性、渐近有效性和不变性等优良统计性质，能够保证在大量样本下估计量的可靠性，还被广泛应用于各类实际问题中，例如消费者需求分析、金融风险管理、劳动经济学乃至产业组织等领域。

随着计算硬件的进步和统计软件的发展，许多复杂模型的最大似然估计都可以借助现代计算工具高效求解，大大降低了实证研究中的技术门槛。最大似然估计的独特魅力在于其将直观的逻辑和严密的数学理论紧密结合，使研究者能够更深刻地理解和刻画复杂的经济现象。展望未来，随着大数据和经济科学的快速发展，最大似然估计将在经济学研究与实际应用中发挥越来越关键的作用。