空间经济学的实证发现

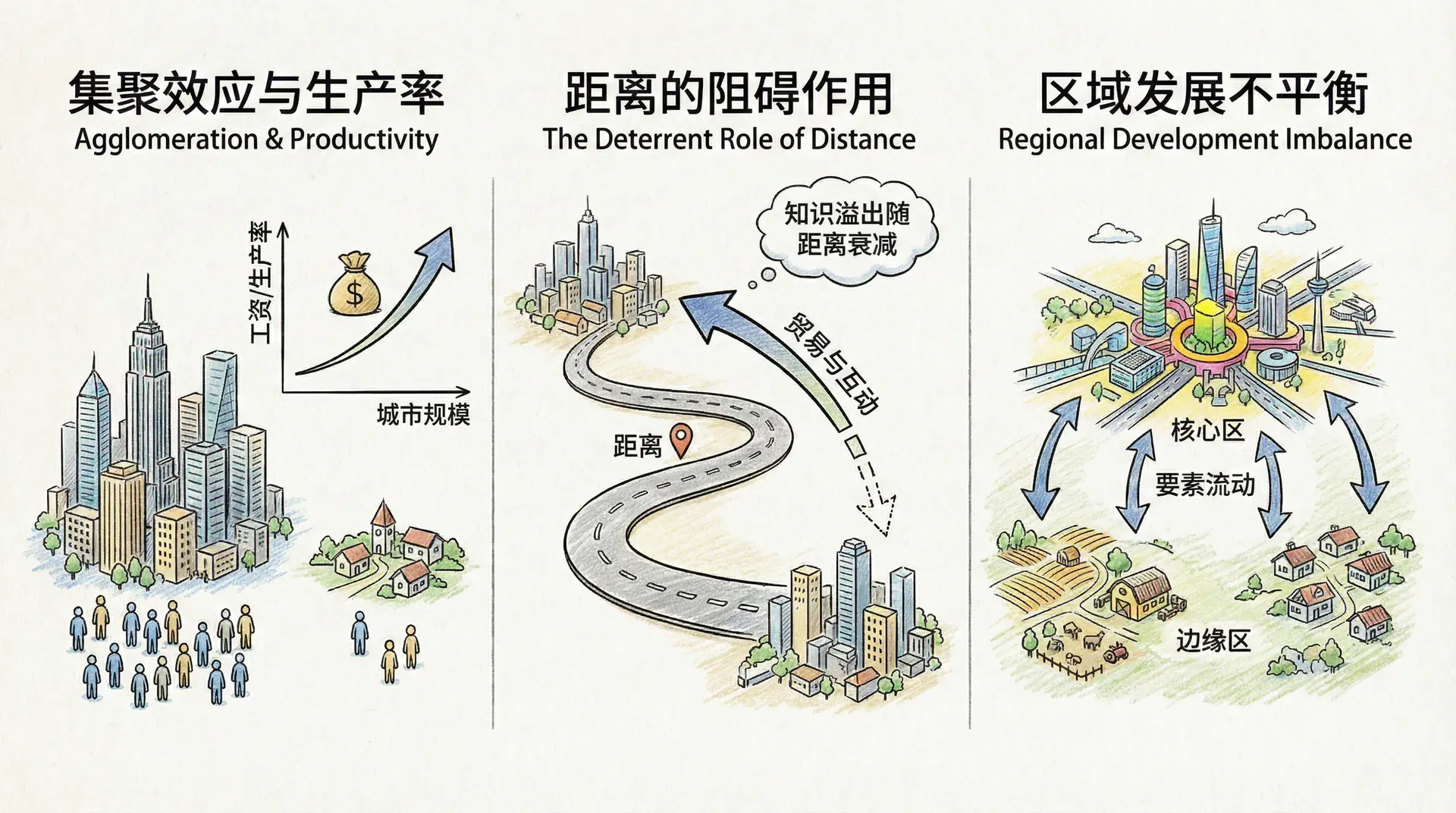
在正式进入空间经济学的理论框架之前，我们有必要先从现实出发，考察一些反复出现在经济活动当中的空间现象。通过梳理大量实际数据和典型案例，我们能够初步把握“空间距离”这一变量对经济行为的深刻影响。例如，无论是人口流动、商品运输，还是城市之间的经济联系，似乎都不可避免地受到地理距离的制约和塑造。

这些实证观察不仅验证了“距离效应”的存在，还揭示了其普遍性与复杂性，为后续理论的提出和模型的构建奠定了坚实的经验基础。因此，理解和分析这些关于距离与经济互动的规律性现象，是我们进入空间经济学世界不可或缺的第一步。

城市规模的排序定律

基本概念的发现

早在20世纪初，人们就开始注意到一个耐人寻味的现象：在某个国家或地区，城市的人口规模 $P$ 与其排名 $r$ 之间往往呈现规律性的数学关系。这个著名的“排名-规模规律”（Rank-Size Rule），最早由奥尔巴赫（Auerbach）等提出，后经齐普夫（Zipf）进一步发展并系统化。

排名-规模规律揭示了城市体系中的一个普遍模式：当我们按照人口规模对城市进行排序时，任何一个城市的人口数量 $P$ 与其排名 $r$ 之间大致满足反比例关系。

用形式化的数学表达，这一规律常被写为：

r \cdot P^q = K

其中：

$r$ ：城市等级排名 ( $r = 1$ 为最大城市)
$P$ ：该城市的人口规模
$q$ ：经验常数（齐普夫定律中常取 $q=1$ 时效果最佳）
$K$ ：与总人口和城市体系相关的常数

当 $q=1$ 时，公式可简化为：

P = \frac{K}{r}

这意味着第二大城市的人口约为第一大城市的一半，第三大为三分之一，依此类推。这一模式被广泛观察于不同国家和历史时期，是空间经济学的重要经验事实。

中国城市体系的现实映照

我们来看一下中国近年来的城市数据，再次体验这个规律的实际指向。以2020年第七次人口普查数据为例：

城市排名	城市名称	常住人口（万人）	理论预测值（万人）	偏差
1	上海	2487	2487	基准
2	北京	2189	1244	+76%
3	深圳	1756	829	+112%
4	重庆	3205	622	+415%
5	广州	1868	497	+276%

可以看到，虽然部分城市，特别是重庆，因行政区划等特殊因素而与理论偏差较大，但整体趋势符合 $P \propto 1/r$ 的规模递减规律。这种偏差恰好突出地反映了现实世界政治、经济、地理和历史等诸多变量对城市体系的作用与塑造。

进而，我们可以将实际数据与排名-规模定律理论值进行对比：

这个图表在对数尺度下往往呈现近似直线型，也佐证了排名-规模规律的“幂律”特征。

距离对经济联系的影响

交通运输中的距离阻力

现代空间经济学研究已经明确，地理距离对各种经济互动均构成了显著的“阻力”（distance decay）效应。这不仅通过运输成本显现，还在于信息传递、人员流动、商业合作等多种层面都有深刻影响。

以2024年春运期间北京始发的高铁客流为例，我们依然可以明显观测到距离对客流量的衰减效应。

结合客流量 $Q$ 和距离 $d$ ，经验上常发现二者呈现指数型或幂律型的衰减关系：

Q = Q_0 \cdot e^{-\lambda d}

或者

Q \propto d^{-\alpha}

其中 $\lambda$ 或 $\alpha$ 为经验衰减系数。这揭示了距离并未失去意义，而是以更隐性的方式影响出行选择与经济连结。

电子商务中的地理效应

即便身处互联网和数字经济时代，地理距离对经济活动的影响依然清晰可见。例如，某电商平台上的一份统计数据显示，买卖双方之间的空间距离不仅影响订单比例，还关联着配送时效与消费者的退货倾向：

从中可以发现，绝大多数订单聚集在相对较近的距离范围内（ $0 - 300$ 公里），随着距离的增加，订单占比显著下降；平均配送时间和退货率则先后上升。这些都直接反映了空间距离在电商效率与消费者体验中的基础作用。

尽管现代化物流和信息技术不断压缩距离带来的表面成本，地理空间的阻力却未曾彻底消失。距离依然通过影响配送时效、运输成本、信息不对称、服务体验等多种路径，持续作用于消费者决策与企业经营。

人口重力模型的应用

引力法则在社会科学中的运用

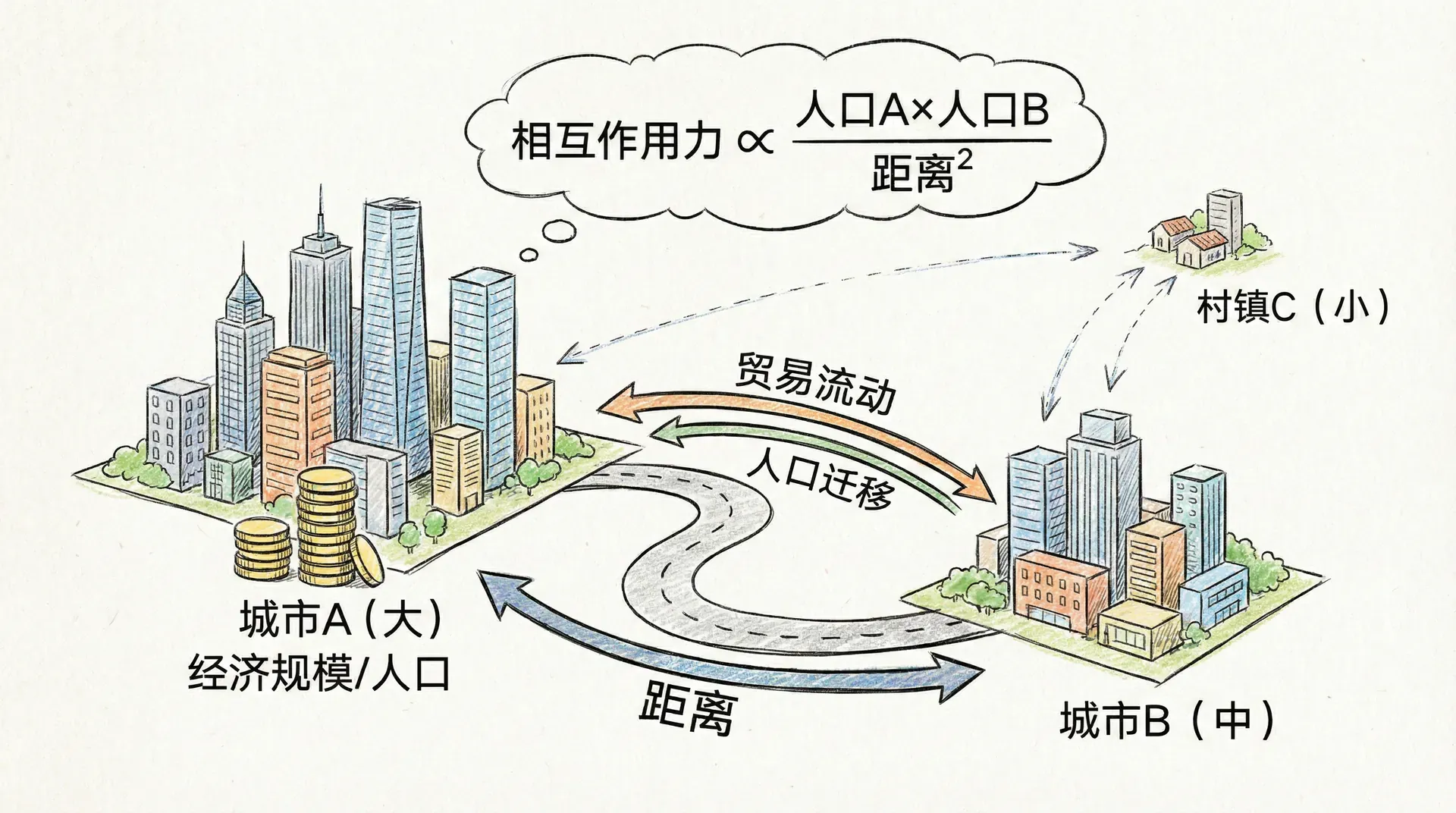
受牛顿万有引力定律的启发，人们在社会科学领域提出了人口重力模型。该模型指出，两个城市之间的经济联系强度，与它们的人口规模的乘积成正比，与两地之间距离的平方成反比。它的基本数学表达式为：

F = \frac{P_1 \cdot P_2}{d^2}

其中：

$F$ ：表示两城市间的经济引力，有时也称为互动强度；
$P_1,\,P_2$ ：分别为两城市的人口规模；
$d$ ：为两城市间的地理距离（通常以公里计量）。

该模型的核心思想是，人口越多、距离越近的城市对彼此的吸引力越强。这种引力不仅适用于经济联系的测度，还广泛用于人口迁移流量、交通流、信息传播等诸多社会现象的分析。

为了更好地贴合实际，有时会在分母上引入调节参数 $\beta$ ，从而一般化为：

F = G \frac{P_1^\alpha \cdot P_2^\gamma}{d^\beta}

其中 $G$ 是比例系数， $\alpha,\,\gamma,\,\beta$ 分别调整人口和距离的影响强度。

现代都市圈的实证分析

以长三角都市圈为例，我们可以应用该模型对主要城市之间的经济联系进行量化分析。2023年长三角地区主要城市相关数据显示，不同距离下经济引力明显呈现衰减趋势：

通过上图可以看出，无论是实际测算的数据，还是理论模型拟合曲线，均显示城市间经济引力随着距离的增加而快速递减。例如，距离上海24公里的苏州，经济引力指数高达850，而随着距离增长至近三百公里，合肥的引力降至仅剩76。这一现象充分体现了距离阻抗的作用，并且表明人口规模和距离确实共同决定了区域互动的强度。

除了城市间的经济联系，重力模型还广泛应用于解释交通流量、产业转移、城市扩张等多种现象。例如，人口迁移流量 $M$ 也常被建模为：

M = k \frac{P_1 \cdot P_2}{d^\beta}

这里 $k$ 为比例常数， $\beta$ 通常取2但也可通过数据拟合确定。

商品流动的空间规律

货运量的距离衰减效应

现代物流大数据为我们观察商品流动与空间距离的关系提供了丰富素材。假设某年中国铁路货运量距离分布显示，发现了明显的距离衰减模式：单位时间内的货运量随运输距离的增加而减少，这种现象往往被称为距离衰减效应。

从上方信息可见，中短距离（200-400公里）区段的货运量最大，显示出大量物流需求集中在区域内的经济网络中。随着运输距离的增加，运量显著递减，反映出运输成本、时间成本等空间摩擦因素的作用。

通常，距离衰减规律可用幂律函数建模：

Q(d) \propto d^{-\alpha}

其中 $Q(d)$ 为距离 $d$ 区间内的货运量， $\alpha$ 是衰减系数。 $\alpha$ 越大，说明对距离越敏感。实际中，不同产业/货物类型其 $\alpha$ 值存在明显差异。

需要注意的是，在某些特殊情况下，距离规律可能会被打破。例如，对于资源型商品（如煤炭、石油）常有长距离、大规模运输现象；而高附加值商品（如高端电子产品、奢侈品）则可以跨越更远的距离实现流通。

不同商品类别的距离敏感度

不同类型商品对运输距离的敏感程度存在显著分歧，这通常与商品的价值密度、腐烂性以及市场特征有关：

商品的价值密度越高，对距离的敏感度越低（ $\alpha$ 越小）。例如，水泥、农产品属于低价值密度、强烈依赖本地市场的类型，对距离极为敏感。而高价值密度、体积小的奢侈品和电子产品，能够跨越更大空间范围流通。

这解释了为何苹果手机可以在全球销售，而水泥则主要在本地消费区域完成流通。

大都市辐射效应的测量

城市影响力的空间衰减

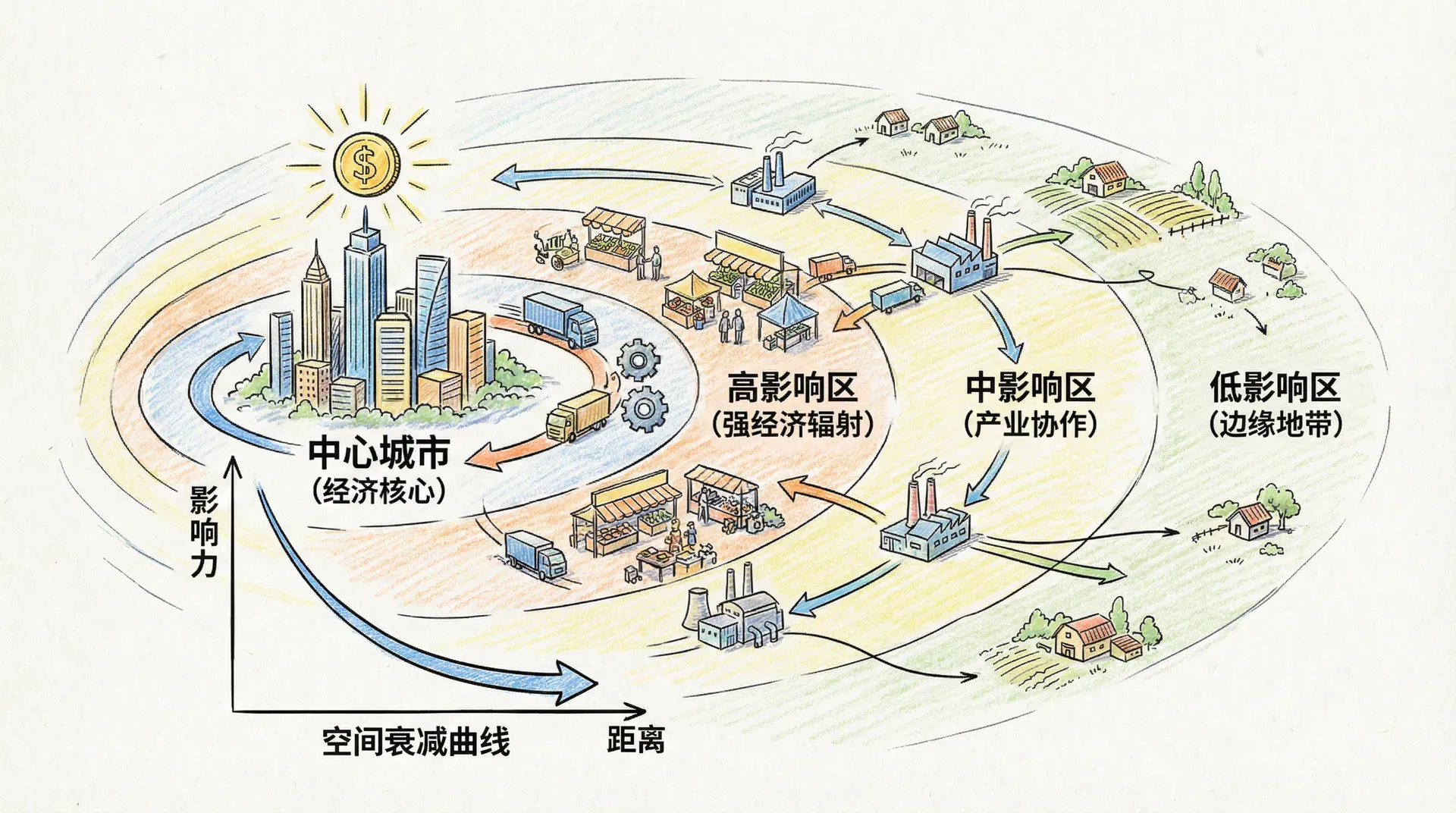
现代都市不仅是人口和经济活动的核心集聚地，也是向周边地区辐射影响的重要源头。以北京为例，观测其对周围区域经济和人口密度的影响，可见明显的空间递减趋势。通常这类辐射现象也可用指数或幂律关系刻画：

I(d) \propto e^{-\lambda d}

其中 $I(d)$ 为距离 $d$ 的影响强度， $\lambda$ 为空间衰减系数。

如图所示，不论是经济密度还是人口密度，均随距北京距离增加而呈现衰减特征。这种空间外溢效应在实际城市体系中极为常见，且远距离区的影响往往趋于零。

具体而言，大都市的辐射影响体现于多个层面：

零售商业活动：单位面积零售额随距离递增而递减；
制造业分布：高技术制造业、现代服务业更倾向于靠近都市圈核心区布局；
服务业发展：金融、咨询等高端服务业主要集聚于核心城市；
基础设施密度：交通网络、通信设施呈现“随距离递减”的配置特征。

理解都市辐射效应及其空间递减规律，对合理制定区域发展战略与基础设施投资有重要启示和参考价值。

总结

通过对这些实证材料的分析，我们可以得出几个重要结论：

距离确实是影响经济活动空间分布的基本因素。无论是城市规模的等级分布、人口流动模式，还是商品贸易流向，都体现出与距离相关的规律性。
这些规律性并非绝对不变。技术进步、政策干预、资源禀赋等因素都会对基本的距离规律产生修正作用。现代通信技术和交通技术的发展，在某种程度上减弱了距离的阻力作用，但并未完全消除这种作用。
这些空间经济规律对于理解现代经济系统具有重要意义。它们不仅帮助我们认识经济活动的空间组织原理，也为区域发展政策、城市规划、交通建设等提供了科学依据。

需要特别注意的是，这些实证规律虽然具有一定的普遍性，但在具体应用时必须考虑当地的历史、文化、政治、自然条件等特殊因素。简单机械地套用这些规律可能导致错误的决策。

在接下来的讨论中，我们将基于这些实证发现，深入探讨空间经济学的理论框架，以及这些理论如何帮助我们更好地理解和预测经济活动的空间模式。