需求分析

前面我们已经学习了消费者选择的基本模型：消费者在给定预算约束下，通过最大化效用来确定最优的消费选择。消费者的最优选择取决于收入和各类商品的价格。通过若干种典型偏好类型的例子，我们初步了解了最优选择的计算过程和具体表现形式。

为了系统研究消费者对价格和收入变化的反应，我们引入需求函数的概念。需求函数描述了在给定商品价格和收入水平下，消费者对每种商品的最优需求量。用数学表达式表示为：

$$\begin{aligned} x_1^* &= x_1(p_1, p_2, m) \\\\ x_2^* &= x_2(p_1, p_2, m) \end{aligned}$$

其中，$x_1^*$ 和 $x_2^*$ 分别是商品1和商品2的最优购买数量，$p_1$ 和 是两种商品的价格， 是消费者的货币收入。

等式左侧表示需求量，右侧是把价格和收入与该商品最优消费数量关联起来的函数形式。

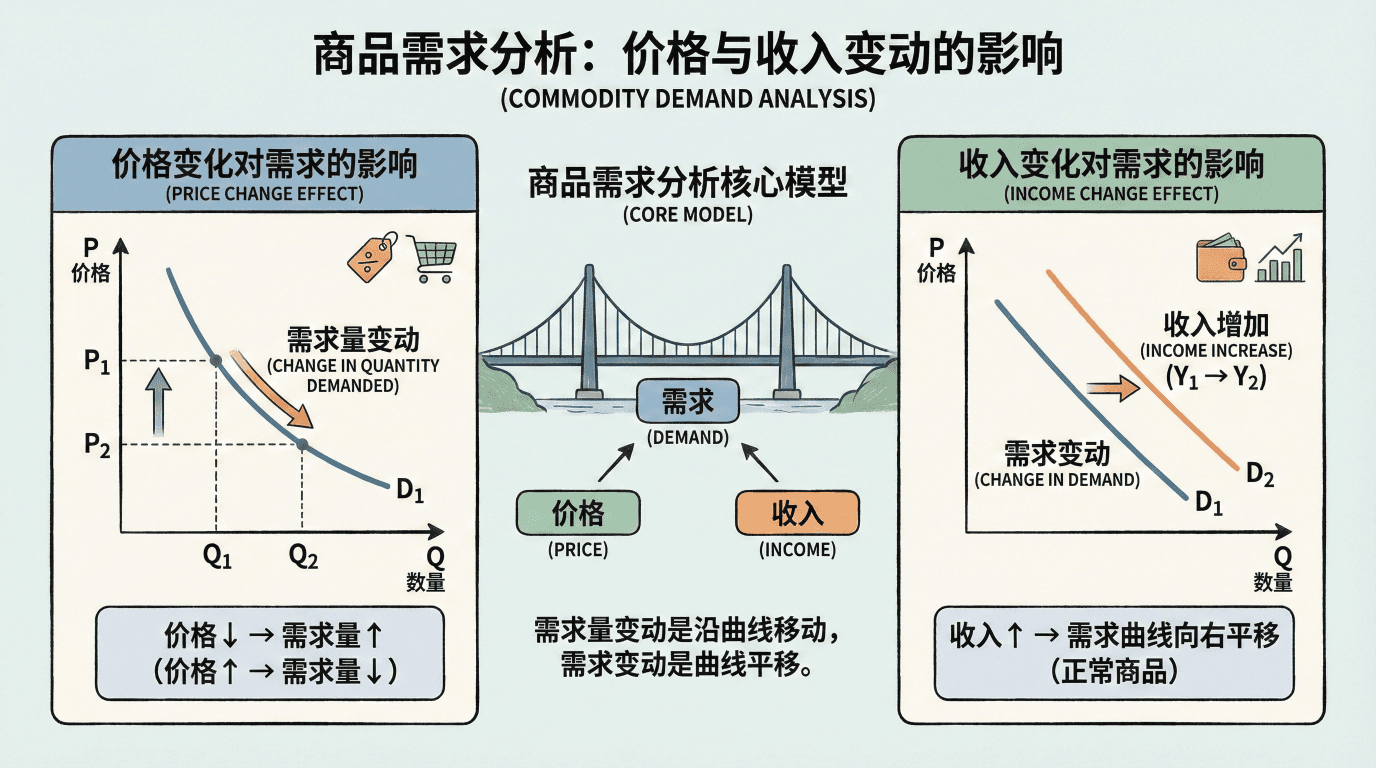
本内容核心目标是分析商品需求如何随着价格和收入的变化而发生变动。研究这种最优选择对外部经济环境变动如何调整，被称为比较静态分析（comparative statics）。

“比较” 意味着要对比经济环境变化前后的均衡状况，分析不同情境下的最优选择。

“静态” 表示我们不考虑动态调整过程，仅着眼于变化前后各自的最终均衡结果。

在标准的消费者理论模型中，影响最优选择的核心变量只有价格和收入。因此，比较静态分析主要涉及以下两个关键问题：

• 当商品价格发生变化时，消费者的最优需求如何调整？
• 当收入水平变动时，消费者会如何重新分配购买各类商品的数量？

---

正常商品与劣等商品

收入变化对需求的影响

我们首先考虑消费者对某种商品的需求如何随收入变化而变化。也就是说，我们关心的是，在收入不同的情况下，消费者对商品的最优选择会发生怎样的变化。在这个分析过程中，我们将假定所有商品的价格保持不变，仅考察由收入变化单独引起的需求变动。

经济学中的一个经典观点是：当其他条件不变时，货币收入的增加会使预算线保持斜率不变、整体平行外移，消费者能够选择的消费组合变多。那么预算线外移以后，消费者在“最优点”上会做出怎样的调整？

直观上，当消费者的收入提升时，消费的“选择空间”增大，一般会购买更多的商品。这一过程可以用下图来表示：

从上图可以看到，收入提升后，最优选择点（由绿色圆点标记）往右上角移动，既消费更多商品$x_1$，也消费更多商品$x_2$。这种现象很普遍，背后反映的是典型的正常商品特征。

正常商品的定义

经济学家通常假设，大多数商品是正常商品。也就是说，当收入增加时，消费者对这些商品的需求量会增加；当收入减少时，需求量则会减少。

用数学语言表达，如果商品 1 是正常商品，则有:

$$\frac{\Delta x_1}{\Delta m} > 0$$

这里，$\Delta x_1$ 表示商品1需求量的变化，$\Delta m$ 表示收入的变化。也就是说，需求的变化方向与收入变化方向相同。

正常商品在现实生活中非常常见。比如家用电器、优质肉类、旅游、娱乐等，当人们收入上升时，大多数人都会提升这些商品和服务的消费水平。

值得一提的是，绝大多数商品在绝大多数收入水平下都是正常商品，特别是在满足基本生活需求之后，更多的收入通常会用于“升级”原有消费的品质或数量。但也要注意，在极端贫困或极端富裕阶段，对某些商品的需求变化可能会不同。

劣等商品的存在

然而，既然有“正常”的商品，也必然会有“异常”存在。指的就是劣等商品，即当收入增加时，需求反而减少的商品。

为什么会存在劣等商品呢？当收入非常低时，人们可能会因为经济原因购买便宜但不优质的商品；但收入提升之后，则更愿意用更高品质的商品替代。例如主食中最便宜的米饭、面条，或者经济困难时才会选择的廉价快餐，随着收入增加，被更健康美味的选择替代。这时，这些商品的需求量可能反而下降。

下图展示了一个收入提升反而导致某种商品需求量下降的例子。在这种情况下，商品$x_1$即为劣等商品：

劣等商品看似很少见，但其实在生活中并不少见。随着社会的发展和生活水平提升，一些原本作为必需的便宜商品，逐步被更高品质或更符合个人喜好的消费替代。

常见的劣等商品实例：

这种收入-需求的“反向”关系，就是劣等商品的核心特征。用数学表达就是：

$$\frac{\Delta x_1}{\Delta m} < 0$$

劣等商品与正常商品的区别和实际意义

• 劣等商品和正常商品的划分标准，并不是由商品本身决定，而是由消费者在不同收入水平下对商品需求的变化决定的。
• 某一个商品在贫困人群中可能是正常商品，但对中产阶级来说可能就是劣等商品。例如方便面：当收入极低时，方便面是廉价主食，收入还在提升阶段消费量不减；但过某个点则持续下降。
• 劣等商品数量远少于正常商品，但它们的经济学意义很大，有助于理解需求随收入变动的复杂性，也帮助我们分析消费升级的过程。

现实生活中，商品需求随着收入变化呈现出多样性。经济学通过正常商品与劣等商品的概念，用以解释不同商品需求对收入变化的不同反应。这对于消费行为研究及相关政策制定具有重要意义。

---

收入提供曲线与恩格尔曲线

收入提供曲线的构造

我们已经看到，随着收入的增加，预算线会在商品组合图（$x_1$-$x_2$平面）上平行向外移动。对于每一个收入水平，最优的消费点即为无差异曲线和预算线的切点。我们可以把这些最优点依次连接起来，形成一条记录收入变化时最优消费组合如何移动的曲线，这条曲线就称为收入提供曲线（Income Offer Curve），也可以叫做收入扩展路径（Income Expansion Path）。

随着收入的提高，预算线不断“外推”，而收入提供曲线就像是在商品1和商品2的组合空间里画出一条“最优点的运行轨迹”。每一个绿色圆点，就是对应于某一个收入水平下的最优商品选择。

经济学意义：

• 曲线上每一个点都反映了在特定收入下的最优消费组合。
• 如果两种商品都是正常商品，路径呈现右上走向，代表随着收入增加，两种商品的消费量都增加。
• 若商品1为劣等品，则收入提升时收入提供曲线可能朝向商品2轴（$x_2$）弯曲，有时甚至会出现“拐弯”、变成后退弯曲形状。

如果两种商品都是正常商品，那么收入扩展路径将具有正斜率。即，收入提升时，两类商品消费量都会上升。

如果某个商品是劣等商品，收入扩展路径可能会向该商品轴弯曲，出现“需求随收入下降”的现象。

假定价格 $p_1$、$p_2$ 固定，收入 $m$ 变化时，最优解 $x_1^*(m), x_2^*(m)$ 描述的点集就是收入提供曲线：

$$\{ (x_1^*(m), x_2^*(m)): m>0\}$$

恩格尔曲线

现在，我们进一步追问：如果我们只关注某一种商品（比如商品1），当收入变化时，该商品的最优需求量 $x_1^*$ 会如何变化？这时候，我们将每个收入水平 $m$ 与最优需求 $x_1$ 配对，作出一条以“收入 $m$ ”为横坐标、“需求 $x_{}$ ”为纵坐标的曲线——这就是（Engel Curve）。

• 恩格尔曲线反映的是：在价格不变的前提下，消费者收入变化如何影响单一商品的需求量变化。
• 形式上，若价格固定为 $(p_1, p_2)$，则恩格尔曲线可表达为 $x_1 = x_1(m)$。

恩格尔曲线（Engel Curve）表示在其他价格不变时，某一种商品的最优需求随收入变化的关系曲线。即：

$$x_1 = x_1(m) \quad (p_1, p_2\, \text{固定})$$

• 对正常商品，恩格尔曲线一般呈现右上上升（斜率为正）：收入增加，需求量也增加。
• 若为劣等商品，恩格尔曲线会在某点后出现拐头向下，收入再高，需求反而减少。

举例说明

• 日常生活中，大米、肉类、住房等，随着收入提升，需求呈现上升趋势，恩格尔曲线右上倾斜。
• 廉价食品（如方便面）、劣质商品，收入低时需求大，收入高时则需求递减，恩格尔曲线会呈“倒U型”或向下弯。

“恩格尔曲线”的命名，来自19世纪德国统计学家恩格尔（Ernst Engel）。他最早用这种方法研究家庭收入如何影响食品等基本生活需求的消费比例，由此发现并提出了著名的“恩格尔定律”。

小结：

1. 收入提供曲线帮助我们看明白在商品分配空间中，收入增加时最优消费点如何变化，是二维的“商品束”视角。
2. 恩格尔曲线专注于单一样品，直接表现收入变动对单品需求的影响，是一维收入-需求关系的视角。

这两类曲线为分析消费结构与需求变化提供了关键工具，也是理解经济增长、社会变迁、消费升级等现象的重要基础。

---

不同偏好类型的实例分析

在学习消费理论的过程中，理解各种典型偏好下的收入提供曲线（Income Expansion Path）和恩格尔曲线（Engel Curve），有助于我们理解消费选择如何受到偏好结构的影响。下面我们将结合基础例子与图形，逐一分析常见的几类偏好。

完全替代品

比如选择支付宝（商品1）和微信支付（商品2）。这两者对于大多数支付场景来说可以相互完全替代。假设支付宝的“使用成本”为p₁，微信为p₂。

最优选择

• 如果p₁ < p₂，消费者将全部收入用于购买支付宝支付服务，完全不买微信服务。此时收入提供曲线表现为水平线——所有点都落在x₂=0上。
• 如果p₂ < p₁，则相反，收入提供曲线为竖直线，所有点都落在x₁=0上。
• 只有在p₁=p₂时，才出现同时消费两种商品，但这类应用很少见。

恩格尔曲线

某一边（如支付宝）上的需求几乎严格等于 x₁ = m/p₁，即简单的正比例关系，恩格尔曲线是一条斜率为1/p₁的直线。

这类商品的恩格尔曲线和收入提供曲线都很直观，消费只集中在更便宜的一个商品上，另一件需求恒为0。

完全互补品

例如每吃饭需要一只左筷子和一只右筷子，两者永远成对消费。

• 收入提供曲线
  不论收入多少，总是x₁ = x₂。收入扩展路径是通过原点的对角线。

• 恩格尔曲线
  以x₁为例，x₁ = m/(p₁ + p₂)，为一条斜率为1/(p₁+p₂)的直线。

柯布-道格拉斯偏好

• 效用函数
  u(x₁, x₂) = x₁ᵃx₂¹⁻ᵃ，其中0 < a < 1

• 需求函数
  x₁ = am/p₁，x₂ = (1-a)m/p₂

  对于给定价格，这两者都是收入m的一次线性函数。也就是说，收入的变化将商品1和2的需求同步等比例增长。

• 收入提供曲线
  仍然是一条从原点射出的直线，斜率和两商品的价格、参数a有关。

• 恩格尔曲线
  以x₁为例：x₁ = (a/p₁)m，也是斜率为a/p₁的直线。

柯布-道格拉斯偏好高度简化消费者现实，却很好地描述许多日常商品的需求规律，是经济学最经典、最核心的偏好假设之一。

齐次偏好

到目前为止我们看到的所有收入提供曲线和恩格尔曲线都很简单——实际上它们都是直线！这是因为我们的例子太简单了。真实的恩格尔曲线不必是直线。

奢侈品与必需品的对比

假设消费者偏好只与两商品数量比值相关，倍增商品数量不会改变消费偏好结构。即若(x₁, x₂) ≻ (y₁, y₂)，则(kx₁, kx₂) ≻ (ky₁, ky₂)。

拟线性偏好

效用函数： u(x₁, x₂) = v(x₁) + x₂，其中v(·)为某个递增函数。

• 收入提供曲线
  通常以“竖直线”表现：无论收入如何增加，只要收入高于某个阈值，商品1的最优消费量x₁*保持不变，所有新增收入全部用来购买商品2。

拟线性偏好下，商品1的需求对收入变化不敏感（边际效用递减到边界时），所有额外收入都会转向商品2。这种现象称作“零收入效应”。

例子

当一个商品在整体预算中的占比极低时，拟线性假设非常适用，比如某些“必备品”、“标准消耗品”。

• 拟线性恩格尔曲线实际上在收入超过某一定值后变成“水平线”；也就是说，商品1的需求达到饱和点，之后任意增加收入，x₁再也不会增长。

---

普通商品与吉芬商品

价格变化的直觉分析

现在让我们详细分析商品的价格变化如何影响需求。假定我们把商品1的价格降低，同时保持商品2的价格和货币收入不变。你会怎么预测商品1需求的变化？

最常见的直觉是：当商品1变便宜，更多的人会倾向于买它，需求增加。这也是经济学中大部分商品（“普通商品”）遵循的规律。

当商品1价格下降时，预算线会向右“旋转”变得更平坦。直观地，纵轴（商品2最大可买量）保持不变，横轴（商品1最大可买量）增大。消费者原来的最优点（在某条无差异曲线上），会因为可支配商品1数量的上升而移动，通常表现为商品1消费变多，商品2持平或略少。

价格变化的两个效应

为了更深入理解价格的影响，经济学家常常把价格下降对需求的影响分为替代效应和收入效应：

• 替代效应：商品1便宜后，相比商品2更有吸引力，消费者倾向于以商品1替代部分商品2。
• 收入效应：商品1变便宜，等于让人“更有钱”，因为在同等价值下可以购买更多，也可能刺激对商品1和商品2的额外消费。

对于大多数商品，这两个效应的合力导致商品1需求增加。

异常情况的可能性

那么，是否所有商品都会因价格下降而需求上升？其实不是。极少数情况下，商品1降价反而需求减少，违背我们常识。

经济学家把这种特殊商品称为吉芬商品（Giffen Goods），名字来自19世纪英国经济学家罗伯特·吉芬。吉芬商品极为罕见，但逻辑上完全可能。

假如商品1是香米饭，商品2是牛奶。一位生活拮据的消费者，每周只能买7碗米饭和7杯牛奶。米饭价格下降，理论上他应该多买米饭，但实际上可能会用节省的钱多买牛奶，把米饭的消费量减少一些。这是怎么回事？

经济学解释

吉芬现象的出现需要两个关键前提：

1. 商品1必须是劣等品：收入增加时你反而减少它的消费（比如主食类，“更有钱就少吃”）。
2. 收入效应非常强烈，强到超过替代效应：价格下降带来的“买得起更多东西感”，促使消费者极大地减少商品1，转向其他商品的消费。

在吉芬商品出现时，替代效应（价格下降倾向于多买）被更强烈的负向收入效应抵消甚至反转了——所以最终商品1降价反而买得更少。

普通商品 vs 吉芬商品

• 普通商品：价格上升→需求减少，价格下降→需求增加。
• 吉芬商品：价格上升→需求反而增加，价格下降→需求反而减少。

在生活中，我们通常遇到的是普通商品，吉芬商品仅在低收入下，对绝对必需品的需求受限，并且“升级”选择比例极大才可能出现。

劣等商品、正常商品、吉芬商品的关系

• 正常商品：收入增加，需求也增加，常见如水果、衣服、家电；
• 劣等商品：收入增加，需求反而减少，如廉价主食、便宜面条等；
• 吉芬商品：既是劣等商品，还满足负向收入效应大于替代效应的特殊条件。

现实中“吉芬商品”的例子非常少，据经济学史研究，历史上真实观测到的吉芬行为主要出现在极端贫困时期（如19世纪爱尔兰土豆飢荒或中国局部主粮实验）。多数现代商品、服务几乎不发生吉芬现象。

---

价格-消费曲线与需求曲线

价格-消费曲线的构造

假设我们让商品1的价格（$p_1$）变化，同时保持商品2的价格（$p_2$）和收入（$m$）不变。几何上，这相当于转动预算线。对于每一个不同的$p_1$，在无差异曲线和预算线的切点处得到最优消费束。将所有这些最优点连起来，就得到一条：

$$\text{价格-消费曲线} = \left\{\left(x_1^*(p_1), x_2^*(p_1)\right)\ \big|\ p_1 \text{变化},\ p_2, m\ \text{固定}\right\}$$

这条曲线展示了当商品1价格变化时，消费者的最优消费如何调整。

需求曲线的导出

对于每一个$p_1$，我们关注商品1的需求量——也就是$x_1^*(p_1)$。将$p_2,m$固定，令在不同值变化，就能画出：

$$x_1^* = x_1(p_1;\ p_2,\ m)$$

需求曲线就是$(p_1,\ x_1^*)$的点的集合，反映在每一个价格下，消费者会选择多少单位的商品1。

商品1的需求函数为$x_1 = x_1(p_1,\, p_2,\, m)$，其中都视为给定常数，通常我们只考察与之间的关系。

斜率特征： 需求曲线一般具有负斜率，即：

$$\frac{\Delta x_1}{\Delta p_1} < 0$$

即价格上升，需求下降，体现了“价格与需求反向变动”的规律。

但对于极少数情况（如吉芬商品），需求曲线可能出现正斜率：

$$\frac{\Delta x_1}{\Delta p_1} > 0$$

此时，价格下降反而需求减少。虽然极为罕见，但在理论和个别案例中是可能出现的。

---

具体偏好类型的需求曲线

不同类型的消费偏好会导致需求函数和需求曲线呈现出非常不同的几何特征，下面详细举例说明常见的几种类型。

完全替代品

例如，美团外卖和饿了么这两个平台，假设二者对你而言是完全替代品，即你只关心谁更便宜，只会选择其中更便宜的那一个消费。

需求函数特征：

• 当 $p_1 > p_2$ 时，$x_1 = 0$（一点都不用美团，只用饿了么）
• 当 $$ 时，（只用美团，把所有钱都花在美团外卖）

这种情况下，商品1的需求曲线呈现为一条“拐角”的折线，当 $p_1>p_2$ 时需求恒为零，$p_1<p_2$ 时需求大幅跳跃。

完全替代品的需求曲线出现了“跳变”：一个价格区间内需求为0，拐点处如果价格相等，理论上有无数个组合；若再下降一步，则全部转向该商品。
现实生活中，类似电话卡流量套餐、燃油/电动汽车切换等场景，常出现类似完全替代的情形。

完全互补品

手机和手机壳是典型的完全互补品，即消费者总是二者配套使用：买一台手机一定会配一个手机壳，多一个手机没壳不用，多一个壳没手机也没用。

对于完全互补品，$x_1 = x_2 = m/(p_1 + p_2)$，无论价格如何，消费者总是以固定比例消费这两种商品。

这类需求曲线的一个显著特点是：对于完全互补品，任何一方价格无论多低，只要另一方价格很高，需求总量都受总价限制——两者永远“一起买一起不用”。类似汽车与轮胎、左脚鞋与右脚鞋、键盘与鼠标等。

离散商品

现在假设商品是只能以整数单位购买的智能手表。消费者决定是否购买第1块、第2块等等，每一块表都可能有自己的“保留价格”。

需求曲线特征：

要求离散商品的需求曲线通常呈现为阶梯状，价格降到特定门槛才会让需求跳跃增加一个单位。

保留价格（Reservation Price）

• 定义： 每一单位离散商品都对应一个保留价格（reservation price）：即消费者刚好愿意（但不愿意再高）购买这一单位的价格。如果市场价高于该价格，就不会买这单位商品。
• 几何对应： 保留价格决定了阶梯的“台阶”落点，只有价格低于下一个保留价格时，才会多买一件。
• 经济含义： 反映的是每一单位的价值递减，边际效用逐步下降。

对于拟线性效用 $u(x_1, x_2) = v(x_1) + x_2$，第 个单位的保留价格公式为：

$$r_k = v(k) - v(k-1)$$

即消费者为第$k$个单位商品所愿意多付的最多价格（等于该单位的“边际效用”）。

例如 $v(n)$ 可能表现为边际递减（如 $v(1)=10, v(2)=17, v(3)=21, ...$），则 $$，依次对应每多一块表消费意愿的降低。 离散商品的需求曲线因此是价格-购买量的阶梯折线。

不同类型偏好导致的需求曲线对比

• 完美替代：需求曲线常出现“拐角”或“跳跃”，在价格相等时存在不确定性和“选择任意分配”的区段。边界分明，一旦价格优势出现，消费全部切换。
• 完美互补：需求曲线变化平滑，但任意一方价格过高时，整体需求都急剧下降。需求对价格变动反应“钝化”，强调搭配消费。
• 离散商品：表现为阶梯，每一阶反映一件商品的边际效用，以及相应的保留价格。现实很多消费场景（门票、大件家电、车票等）都呈现离散决策。

通过练习分析这些特殊的需求曲线，可以更好地理解日常消费行为隐含的理性选择原则，以及价格变化如何影响实际购买数量。

---

替代品与互补品

正式定义

虽然我们已经在前面多次用到“替代品”和“互补品”这两个术语，但现在是系统梳理和精确定义它们的好时机。

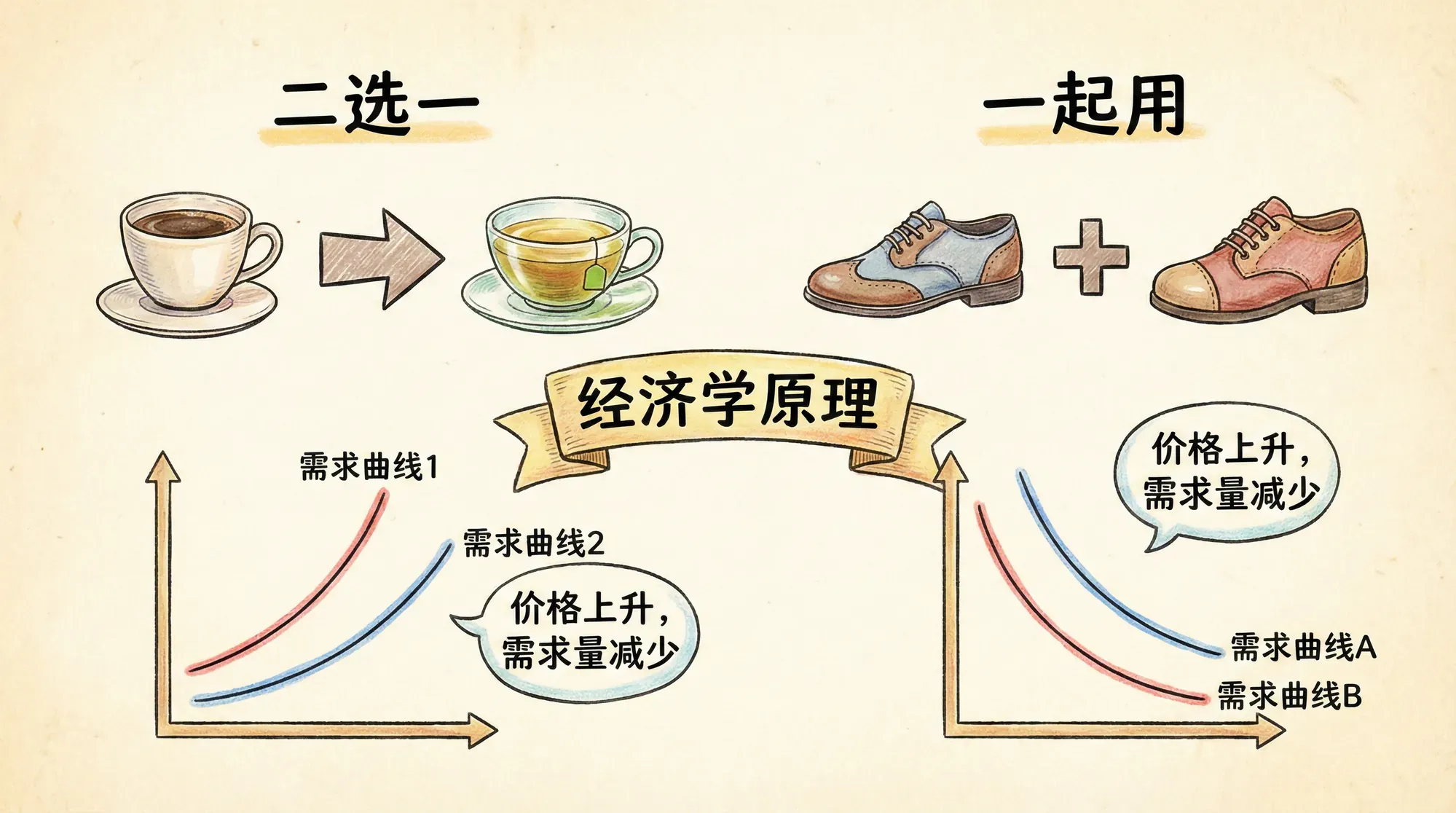
替代品的定义：
如果当某一商品（商品2）的价格上升时，消费者对另一商品（商品1）的需求增加，我们称商品1是商品2的替代品。用需求对价格的变化率表达为：

$$\frac{\Delta x_1}{\Delta p_2} > 0$$

即商品2价格上升 $\rightarrow$ 商品1需求增加。

经济直觉：
替代品描述的是“二选一”的消费关系。当商品2比以前更贵时，消费者会减少对商品2的购买，并转而增加对商品1的消费。例如，咖啡涨价时，消费者买茶的可能性增加，公交车票变贵时，更多人可能选择地铁等。现实生活中，替代品未必完全可以互换，但它们至少满足类似的需求或有一定功能重合。

互补品的定义：
如果当商品2的价格上升时，对商品1的需求反而减少，则商品1是商品2的互补品。即：

$$\frac{\Delta x_1}{\Delta p_2} < 0$$

解释起来，就是商品1和商品2通常需要搭配消费，一种变贵导致两种都不愿多买。

经济直觉：
互补品强调“一起消费”。例如，汽车和汽油，打印机和墨盒，咖啡和糖，通常是成对出现：其中一样涨价时，两样的购买量往往都会下滑。也有强弱之分：比如鞋和鞋带关系比咖啡和糖更密切，属于“完全互补”（极端情况下必须一比一配套）。

数学公式与图形表示

我们也可以用需求函数的偏导数来更加正式地表示替代品与互补品。

• 对于替代品，如果 $\frac{\partial x_1}{\partial p_2} > 0$。
• 对于互补品，如果 $\frac{}{}$。

此外，在二维商品空间，需求函数 $x_1^*(p_1, p_2, m)$ 若对 $p_2$ 的反应为正说明二者是替代品，反应为负说明是互补品。 在需求曲线上，替代品的价格上升会使另一商品需求曲线向右移动，互补品则向左移动。

实际例子分析

常见替代品与互补品示例表

你还可以试着思考日常生活中，什么商品有替代还是互补的关系？比如牛奶和豆浆、手机和电话卡、笔记本电脑与外接电源等，每种关系都会影响市场的需求变化。

• 替代品的需求曲线对方的价格变化非常敏感，典型情况是某一物品涨价，需求会很快被“抢走”；
• 互补品需求则像“连体”一样，缺一不可——你不买球鞋，也没必要买鞋带。

更深入的讨论与局限性

两个重要警告：

1. 两商品情况的特殊性：
   在只有两种商品的情况下，由于消费者总收入是固定的，如果你在商品1上花的钱增多，必然要在商品2上缩减，这种“预算约束”导致许多数学关系自动成立，限制了观察到的行为类型。当市场中商品多于两种时，这种限制就不存在了，可以有更复杂的替代/互补结构。

2. 多商品情况的复杂性：
   当涉及三种及以上商品时，很容易出现：商品1是商品3的替代品，但商品3却又是商品1的互补品，关系不再对称。
   比如：红茶是咖啡的替代品，但牛奶是同时和咖啡/红茶配套的互补品，三者间的经济学关系就很微妙。

---

反需求函数

反需求函数的定义

如果我们保持 $p_2$ 和 $m$ 固定，绘制 $p_1$ 关于 $x_1$ 的函数关系，我们就获得了需求曲线（Demand Curve）。反需求函数（Inverse Demand Function）则是将这个关系反过来——表达价格 随着需求数量 的变化而变化。只要我们确实拥有一条向下倾斜的需求曲线（这是绝大多数正常商品的典型情况），反需求函数的讨论就极具实际意义。

• 需求函数 $x_1^* = f(p_1)$：给定价格 $p_1$，消费者愿意并能够购买多少单位的商品1。

它们虽然都是描述“价格-数量”关系，但一个以价格为自变量，另一个以数量为自变量，经济意义迥然不同。

以柯布-道格拉斯偏好为例，若对商品1的需求为：$x_1^* = \dfrac{a m}{p_1}$，则反需求函数为：

• 直接需求函数：$x_1^* = am / p_1$
• 反需求函数：$p_1 = am / x_1^*$

也就是说：想要诱使消费者“刚好”买 $x_1$ 单位的商品1，价格 $p_1$ 需要设定为多少。

在实际政策与价格制定分析中，反需求函数常用于推断消费者剩余和社会总福利等。通过将反需求函数的图像下方、市场价格之上的面积累加起来，可衡量消费者剩余。

边际支付意愿

反需求函数有一个重要且直观的经济学诠释。回忆最优消费必须满足：

$$|\mathrm{MRS}| = \frac{p_1}{p_2}$$

即在最优点，商品1相对于商品2的边际替代率的绝对值，恰好等于两者的价格比。这说明在对应消费量 $x_1$ 上：

$$p_1 = p_2 |\mathrm{MRS}|$$

因此，反需求函数 $p_1(x_1)$ 本质上就是边际支付意愿（Marginal Willingness to Pay，MWTP）：消费 $x_1$ 单位商品1时，消费者在边际上最多愿意为“再多一单位商品1”所放弃的商品2的数量（或货币）。

特殊情况分析： 假设商品2为“货币”，其价格 $p_2=1$，则

• $p_1 = |\mathrm{MRS}|$，即商品1的价格直接反映了为额外获得商品1而愿意放弃的货币数额。

在反需求函数曲线与市场价格 $p_1^*$ 之间、从零到已消费 $x_1^*$ 之间围成的面积，被称为消费者剩余（Consumer Surplus）。这部分面积衡量了消费者因低于他们愿意支付的价格购得商品而带来的“幸福感”或经济福利。

向下倾斜需求曲线的新含义

从边际支付意愿的视角，向下倾斜需求曲线又有了这样的经济学含义：

边际支付意愿递减原理： 当 $x_1$ 很小时，消费者极度渴望该商品，愿意为多一单位支付很高的价格；当 $x_1$ 增大，消费者的需求逐渐满足，再多一单位的价值（边际支付意愿）递减。这正是反需求函数随 $x_1$ 增加而下降的根本原因。

这体现了经济学中 边际效用递减（Diminishing Marginal Utility） 的基本原则：拥有越多，额外获得的价值越小。

反需求函数与实际应用

在完全竞争市场中，市场价格是由供给与需求交点决定。反需求函数直接反映了每个可能消费水平下的支付意愿，供给函数则反映每个数量下的最小愿意接受价格。

动态竞价、价格歧视与福利分析

• 动态定价与拍卖：企业可以根据每个消费者的边际支付意愿设定不同价格，即“一级价格歧视”，理论上能榨取全部消费者剩余。
• 价格歧视：反需求函数揭示了不同需求量的支付能力，为差别定价提供基础。
• 公共品项目评价：通过调研和模拟反需求函数，能够量化消费者对不同消费水平下的支付意愿，进而进行社会项目可行性分析。
• 福利变化测算：政策干预导致价格或供给变化时，通过积分反需求函数可以计算消费者剩余变化，作为福利分析的重要部分。

边际支付意愿的应用总结表

---

总结

需求分析为我们提供了系统理解消费者如何响应价格和收入变化的理论基础，通过比较静态方法揭示了商品需求随经济环境变化而调整的机制。收入增加时，正常商品需求上升，劣等商品则可能下降，不同商品对收入变动的敏感性可以通过收入提供曲线和恩格尔曲线分析。价格变动影响需求，也是区分普通商品和吉芬商品的依据。产品间存在替代与互补关系，价格和需求的联动决定了市场上的消费结构。

消费者的决策还与偏好类型密切相关，无论是齐次、拟线性偏好还是完全替代、互补品，均会体现在收入和价格的效应路径及需求曲线的不同形态。通过反需求函数，我们能刻画边际支付意愿递减的规律，这为产品定价、政策评估和福利分析奠定了基础。

分辨商品类型，解析收入和价格变化对消费的影响，理解商品间的关系，运用反需求函数分析福利，并形成系统比较与边际分析的经济学思维。需求理论不仅在市场定价、消费者行为、政策制定等领域有现实意义，还为拓展弹性理论、福利分析、市场需求聚合及动态和不确定性下的消费决策等进一步学习提供了坚实基础。

需求分析作为微观经济学的核心，为企业与政府提供科学决策支持，也是理解和解决现实经济问题的重要理论工具。