密码学
密码学是计算机安全的数学基础。从密码存储到加密通信,从数字签名到密钥交换,几乎所有安全机制都依赖于密码学。但密码学不仅仅是数学理论,更是实际应用中的工程实践。理解密码学的基本原理,以及如何在实践中正确使用密码学,是这一节要讨论的内容。
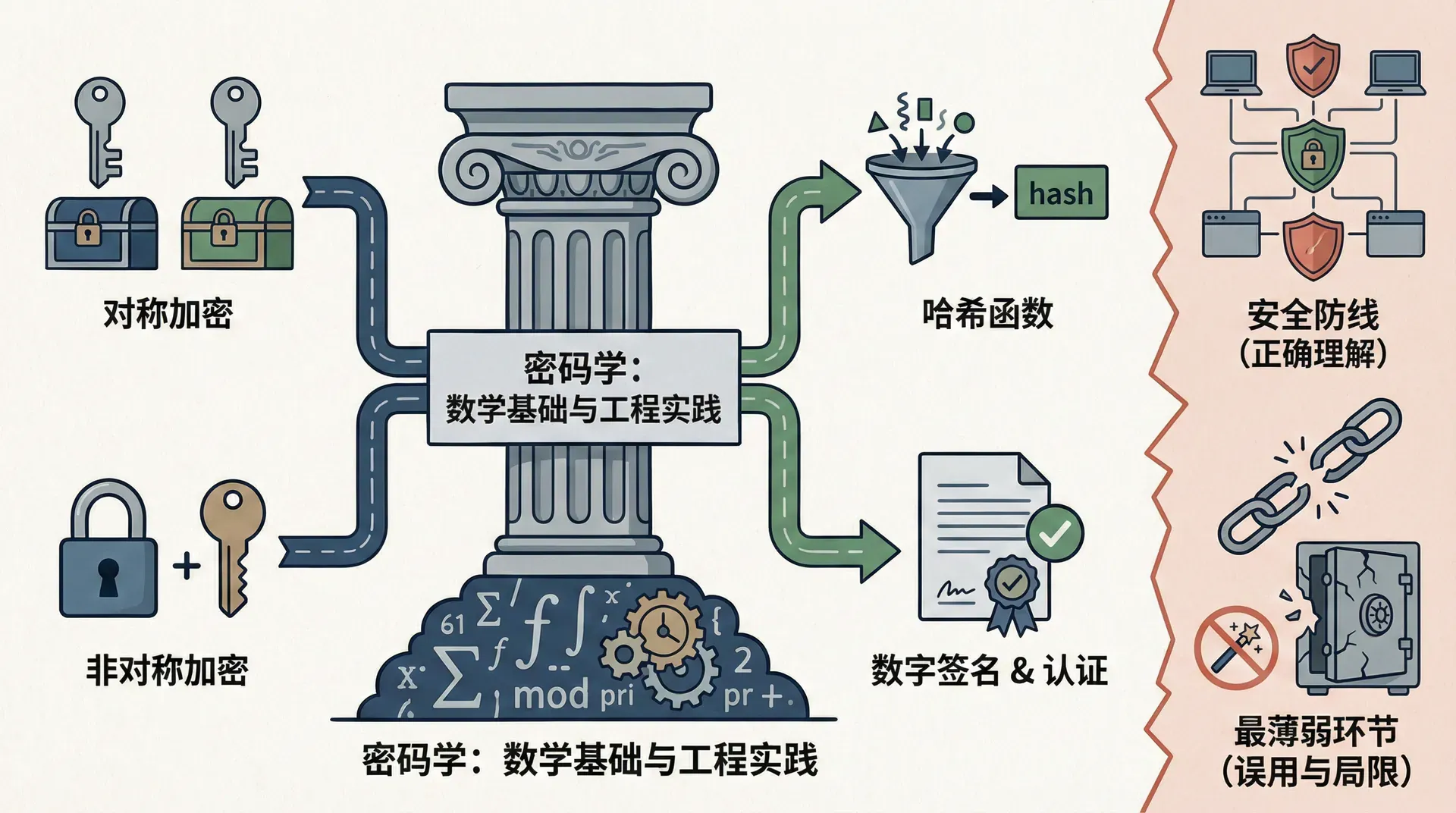
密码学不是魔法。它不能解决所有安全问题,但如果使用不当,它可能成为安全系统中最薄弱的环节。理解密码学的原理和局限性,是安全工程师的基本素养。
这一节不会深入数学推导,而是关注密码学的实际应用。我们将讨论对称加密、非对称加密、哈希函数、消息认证码、数字签名等基本概念,以及它们在实际系统中的使用。我们还将讨论常见的密码学错误,以及如何避免这些错误。
对称加密
对称加密使用相同的密钥进行加密和解密。发送方使用密钥加密明文得到密文,接收方使用相同的密钥解密密文得到明文。对称加密的优点是速度快、效率高,适合加密大量数据。
对称加密的数学表达是: 和 ,其中 是加密函数, 是解密函数, 是密钥, 是明文, 是密文。
对称加密的安全性依赖于密钥的保密性。如果攻击者获得了密钥,他们就可以解密所有使用该密钥加密的数据。因此,密钥管理是对称加密的关键挑战。
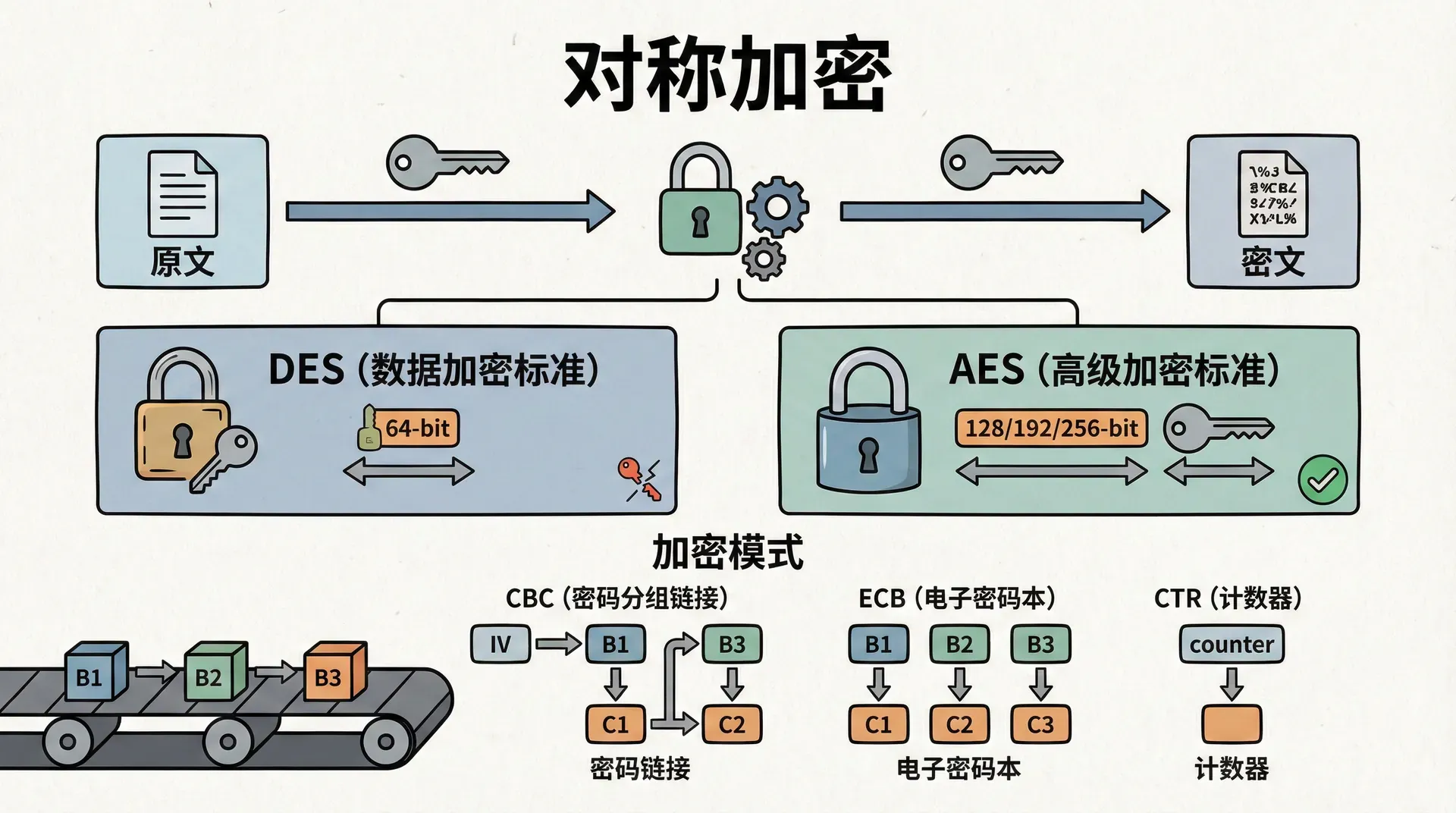
DES和AES
DES(Data Encryption Standard)是早期的对称加密标准,使用56位密钥。随着计算能力的提高,DES已经不再安全,可以被暴力破解。3DES是DES的变体,使用三个DES密钥,提供更高的安全性,但速度较慢。
AES(Advanced Encryption Standard)是现代对称加密标准,支持128位、192位和256位密钥。AES是目前最广泛使用的对称加密算法,被认为是安全的,只要正确使用。
|from cryptography.fernet import Fernet from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes from cryptography.hazmat.backends import default_backend import os # 使用Fernet(基于AES)进行对称加密 def encrypt_symmetric(plaintext, key): """使用对称加密加密数据""" f = Fernet(key) ciphertext = f.encrypt(plaintext.encode()) return ciphertext def decrypt_symmetric(ciphertext, key): """使用对称加密解密数据""" f = Fernet(key)
上面的代码示例使用了cryptography库的Fernet,它已经处理了密钥派生、IV生成、填充等细节。在实际应用中,应该使用经过充分测试的密码学库,而不是自己实现加密算法。
加密模式
对称加密算法(如AES)是块密码(Block Cipher),一次只能加密固定大小的数据块(AES是128位)。要加密任意长度的数据,需要使用加密模式(Mode of Operation)。
- ECB模式(Electronic Codebook):每个数据块独立加密。这种模式不安全,因为相同的明文块会产生相同的密文块,泄露了数据模式。
- CBC模式(Cipher Block Chaining):每个数据块与前一个密文块异或后再加密。这需要初始化向量(IV),IV应该是随机的,不能重复使用。
- CTR模式(Counter):使用计数器生成密钥流,与明文异或。这种模式可以并行加密,适合高性能场景。
- GCM模式(Galois/Counter Mode):结合CTR模式和认证,提供加密和认证。这是现代应用推荐使用的模式。
|from cryptography.hazmat.primitives.ciphers.aead import AESGCM def encrypt_with_gcm(plaintext, key): """使用AES-GCM进行加密(提供认证)""" aesgcm = AESGCM(key) # 生成随机nonce(在GCM中,nonce通常是12字节) nonce = os.urandom(12) ciphertext = aesgcm.encrypt(nonce, plaintext.encode(), None) return nonce + ciphertext def decrypt_with_gcm(ciphertext, key): """使用AES-GCM进行解密""" aesgcm = AESGCM(key) nonce =
对称加密的最大挑战是密钥管理。密钥必须安全地生成、存储、传输和销毁。如果密钥泄露,所有使用该密钥加密的数据都可能被解密。
在实际系统中,密钥管理可能包括:
- 密钥生成:使用密码学安全的随机数生成器
- 密钥存储:使用密钥管理系统(KMS)或硬件安全模块(HSM)
- 密钥传输:使用非对称加密或密钥交换协议
- 密钥轮换:定期更换密钥,限制密钥泄露的影响
- 密钥销毁:安全地删除不再使用的密钥
密钥管理是密码学中最薄弱的环节。许多安全漏洞不是由于加密算法的问题,而是由于密钥管理不当。永远不要硬编码密钥,永远不要将密钥存储在代码中,永远不要通过不安全的渠道传输密钥。
非对称加密
非对称加密使用密钥对:公钥(Public Key)和私钥(Private Key)。公钥可以公开,用于加密数据。私钥必须保密,用于解密数据。非对称加密解决了对称加密的密钥分发问题,但速度较慢,不适合加密大量数据。
非对称加密的数学表达是: 和 ,其中 是公钥, 是私钥。公钥和私钥是数学相关的,但从公钥推导私钥在计算上是不可行的。
非对称加密的安全性依赖于数学难题,如大数分解(RSA)或离散对数(椭圆曲线)。这些难题在经典计算机上是困难的,但在量子计算机上可能变得容易,这就是为什么需要后量子密码学。
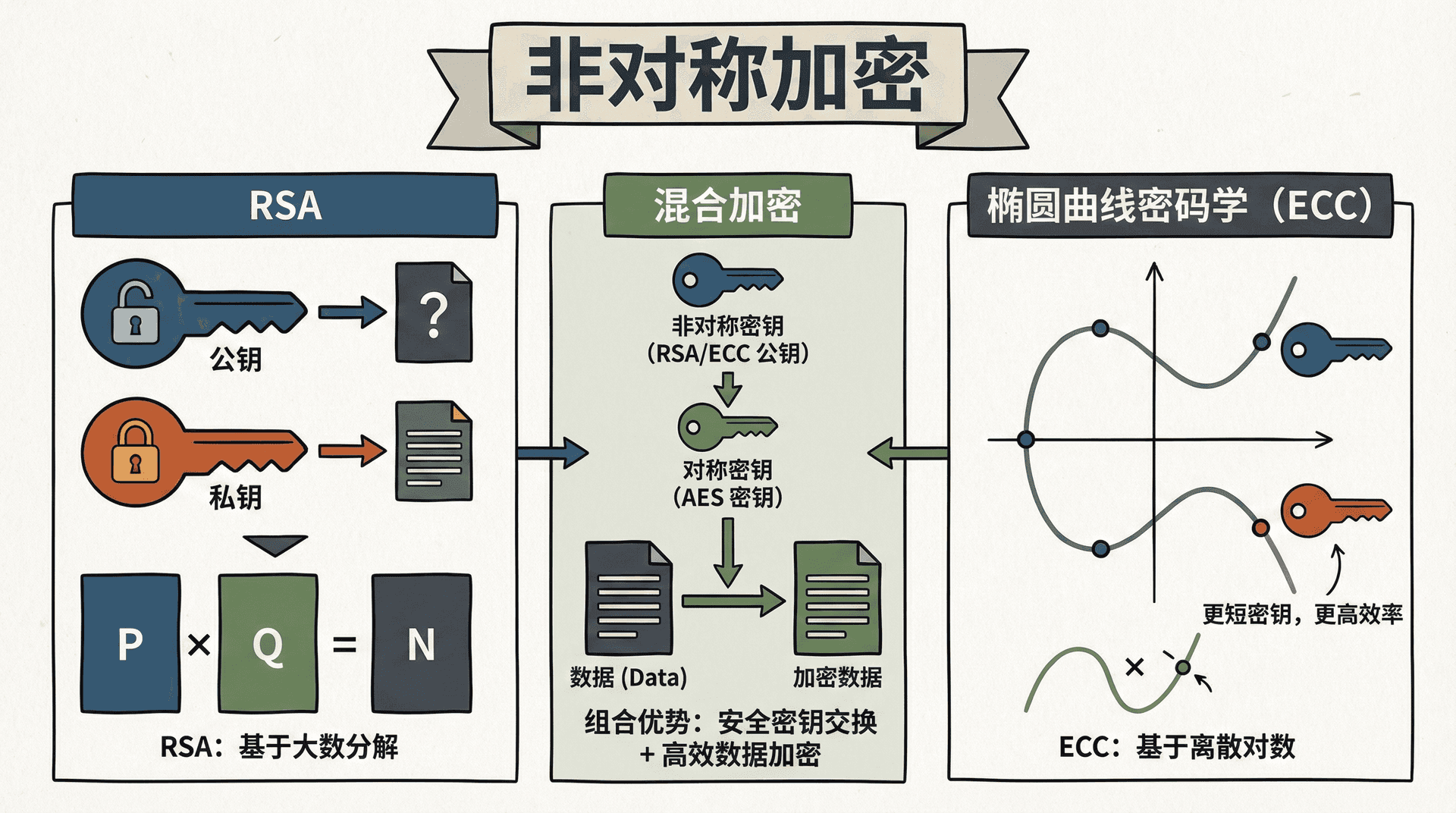
RSA
RSA是最著名的非对称加密算法,基于大数分解难题。RSA的安全性依赖于分解大整数的困难性。随着计算能力的提高,RSA密钥长度需要不断增加。目前推荐使用至少2048位的RSA密钥,对于长期安全,建议使用3072位或4096位。
|from cryptography.hazmat.primitives.asymmetric import rsa, padding from cryptography.hazmat.primitives import hashes from cryptography.hazmat.backends import default_backend def generate_rsa_keypair(): """生成RSA密钥对""" private_key = rsa.generate_private_key( public_exponent=65537, key_size=2048, backend=default_backend() ) public_key = private_key.public_key() return
RSA加密有大小限制。对于2048位密钥,最多只能加密245字节的数据。要加密更大的数据,通常使用混合加密:使用非对称加密加密对称密钥,使用对称加密加密实际数据。
椭圆曲线密码学
椭圆曲线密码学(ECC)使用椭圆曲线上的点运算,提供与RSA相同的安全性,但使用更短的密钥。256位ECC密钥的安全性相当于3072位RSA密钥。这使得ECC在资源受限的环境中特别有用。
|from cryptography.hazmat.primitives.asymmetric import ec from cryptography.hazmat.primitives import serialization def generate_ecc_keypair(): """生成椭圆曲线密钥对""" private_key = ec.generate_private_key(ec.SECP256R1(), default_backend()) public_key = private_key.public_key() return private_key, public_key # ECC通常用于密钥交换和数字签名,而不是直接加密 # 加密通常使用ECDH(椭圆曲线Diffie-Hellman)进行密钥交换
混合加密
在实际应用中,通常使用混合加密:使用非对称加密加密对称密钥,使用对称加密加密实际数据。这结合了非对称加密的密钥分发优势和对称加密的速度优势。
|def hybrid_encrypt(plaintext, public_key): """混合加密:使用非对称加密加密对称密钥,使用对称加密加密数据""" # 生成对称密钥 symmetric_key = Fernet.generate_key() f = Fernet(symmetric_key) # 使用对称加密加密数据 encrypted_data = f.encrypt(plaintext.encode()) # 使用非对称加密加密对称密钥 encrypted_key = encrypt_rsa(symmetric_key.decode(), public_key) return encrypted_key + b'|||' + encrypted_data def hybrid_decrypt(ciphertext, private_key): """混合解密"""
哈希函数
哈希函数将任意长度的数据映射到固定长度的哈希值。哈希函数应该是单向的(从哈希值无法推导原始数据)、确定性的(相同输入产生相同输出)、雪崩效应的(输入的小变化导致输出的大变化)。
哈希函数的应用
- 密码存储:存储密码的哈希值而不是明文密码。当用户输入密码时,计算哈希值并与存储的哈希值比较。
- 数据完整性:计算数据的哈希值,如果数据被修改,哈希值会改变。这可以用于检测数据是否被篡改。
- 数字签名:对数据的哈希值进行签名,而不是对数据本身签名。这提高了效率,因为哈希值通常比原始数据小得多。
- 承诺方案:使用哈希值作为承诺,稍后揭示原始数据来证明承诺。
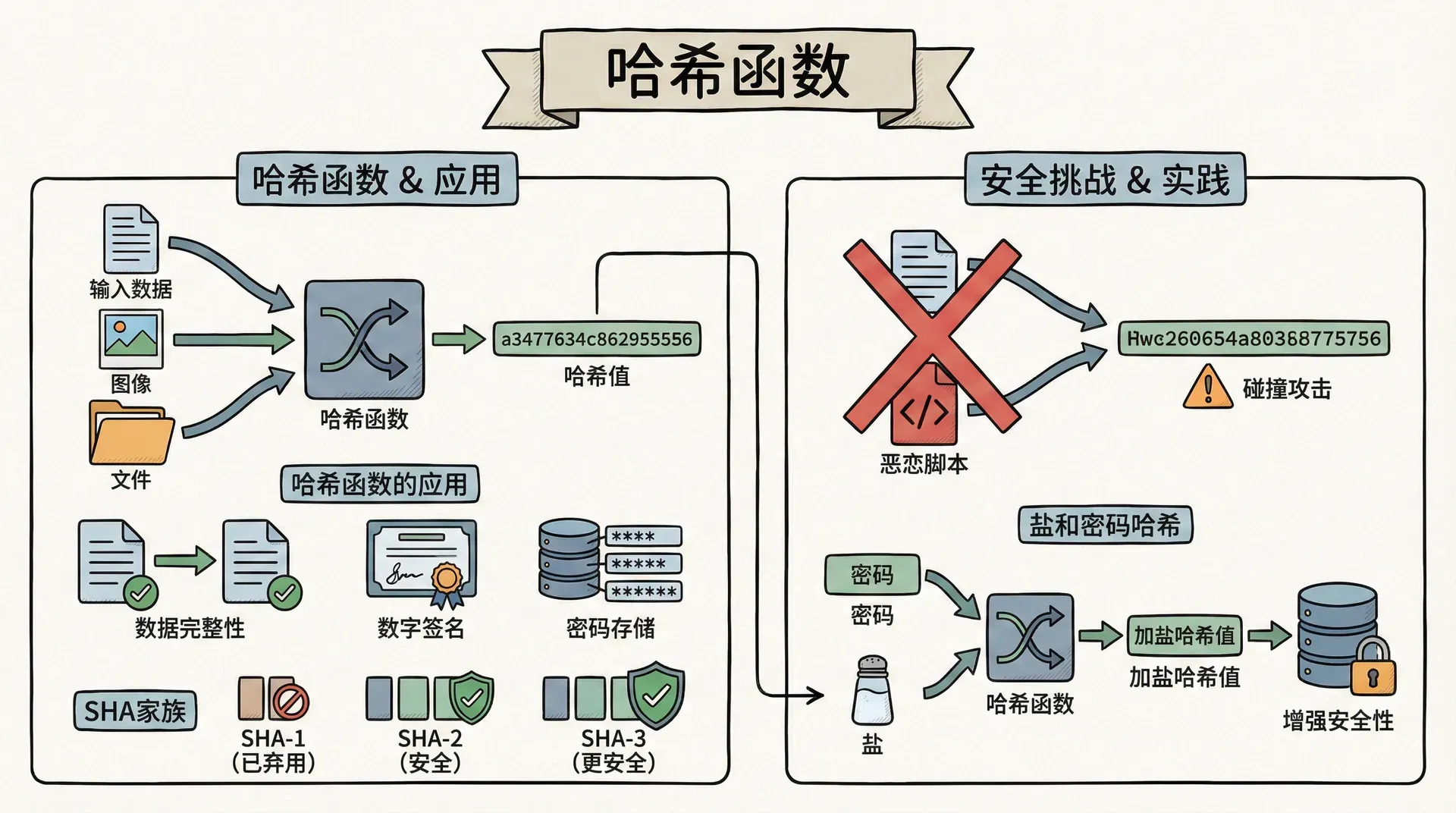
SHA家族
SHA(Secure Hash Algorithm)是常用的哈希函数家族。SHA-1已经不再安全,应该避免使用。SHA-256和SHA-512是目前推荐使用的哈希函数。
|import hashlib def hash_data(data): """计算数据的SHA-256哈希值""" return hashlib.sha256(data.encode()).hexdigest() # 示例 message = "这是需要哈希的数据" hash_value = hash_data(message) print(f"哈希值: {hash_value}") # 即使数据有微小变化,哈希值也会完全不同 message2 = "这是需要哈希的数据." hash_value2 = hash_data(message2) print(f"修改后的哈希值: {
碰撞攻击
哈希函数的理想特性是抗碰撞性:找到两个不同的输入产生相同的哈希值在计算上是不可行的。但随着计算能力的提高,一些哈希函数(如MD5、SHA-1)已经被证明存在碰撞攻击。
MD5和SHA-1已经不再安全,不应该用于安全应用。应该使用SHA-256或SHA-512,或者使用专门设计的密码学哈希函数,如BLAKE2。
盐和密码哈希
如前所述,密码哈希必须使用盐来防止彩虹表攻击。现代密码哈希函数(如bcrypt、scrypt、Argon2)不仅使用盐,还故意设计得计算成本高,使得暴力破解变得困难。
|import bcrypt def hash_password(password): """使用bcrypt哈希密码(自动生成盐)""" # bcrypt自动生成盐并包含在哈希值中 hashed = bcrypt.hashpw(password.encode(), bcrypt.gensalt()) return hashed def verify_password(password, hashed): """验证密码""" return bcrypt.checkpw(password.encode(), hashed) # 示例 password = "我的密码" hashed = hash_password(password) print(f"哈希值: {hashed}")
消息认证码(MAC)
消息认证码(Message Authentication Code,MAC)用于确保消息的完整性和真实性。MAC使用共享密钥计算,只有拥有密钥的人才能生成或验证MAC。
HMAC
HMAC(Hash-based MAC)是最常用的MAC算法,使用哈希函数和密钥计算MAC。
|import hmac import hashlib def generate_hmac(message, key): """生成HMAC""" return hmac.new(key.encode(), message.encode(), hashlib.sha256).hexdigest() def verify_hmac(message, key, received_hmac): """验证HMAC""" calculated_hmac = generate_hmac(message, key) return hmac.compare_digest(calculated_hmac, received_hmac) # 示例 message = "这是需要认证的消息" key = "共享密钥" mac = generate_hmac(message, key) print(f"MAC:
HMAC提供了消息完整性和真实性保证。如果消息被修改,MAC会改变。如果攻击者不知道密钥,他们无法生成有效的MAC。这使得接收方可以检测消息是否被篡改或伪造。
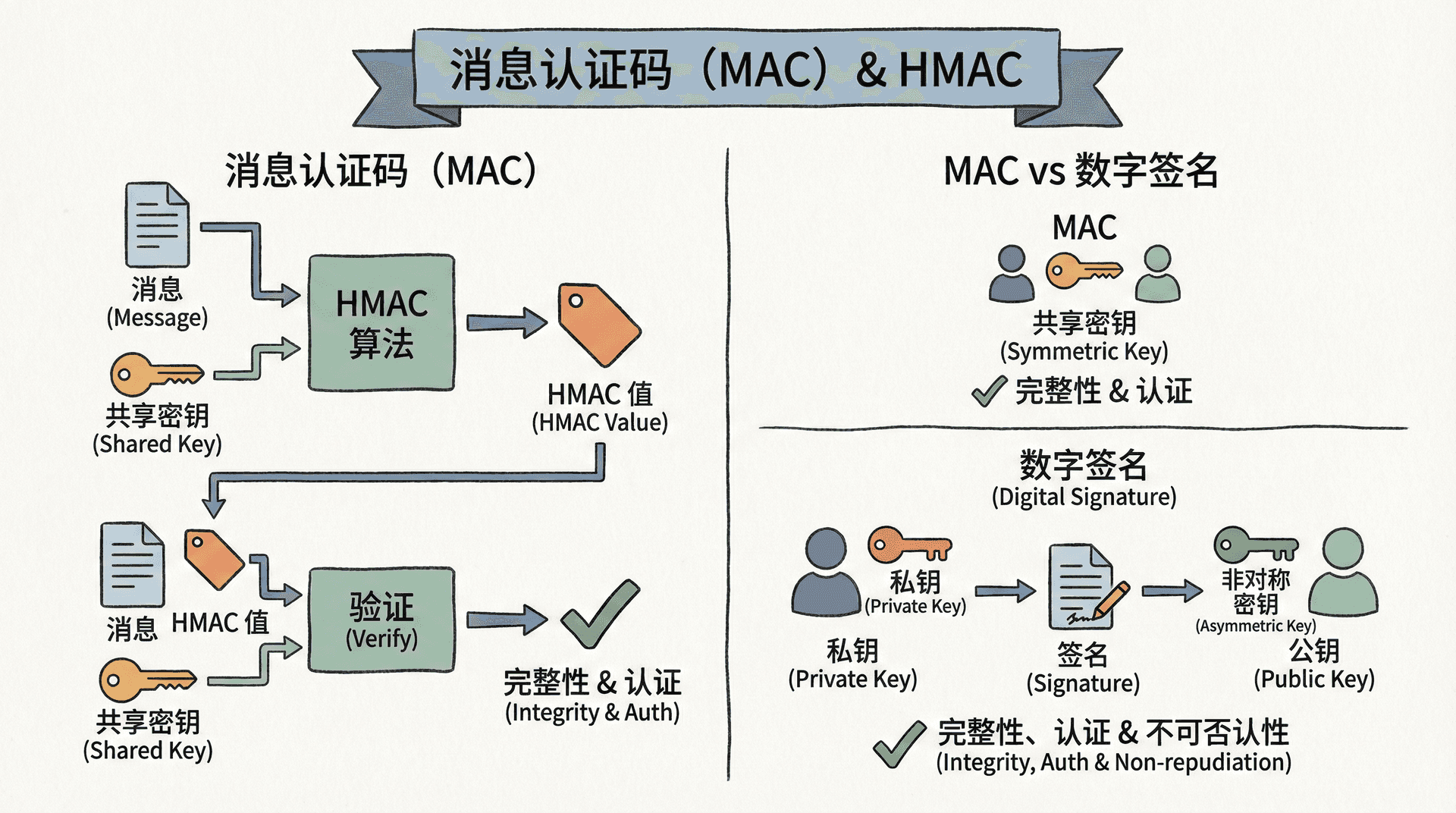
MAC vs 数字签名
MAC和数字签名都提供消息完整性和真实性,但它们有重要区别:
- MAC使用共享密钥,数字签名使用密钥对
- MAC提供认证,但不提供不可否认性(因为双方都知道密钥)
- 数字签名提供不可否认性(因为只有签名者知道私钥)
选择MAC还是数字签名取决于应用场景。如果只需要在双方之间认证消息,MAC可能更简单高效。如果需要不可否认性,必须使用数字签名。
数字签名
数字签名提供消息完整性、真实性和不可否认性。签名者使用私钥签名消息,验证者使用公钥验证签名。只有拥有私钥的人才能生成有效签名,这提供了不可否认性。
数字签名的原理
数字签名通常对消息的哈希值进行签名,而不是对消息本身签名。这提高了效率,因为哈希值通常比原始消息小得多。
|from cryptography.hazmat.primitives.asymmetric import padding from cryptography.hazmat.primitives import hashes def sign_message(message, private_key): """使用私钥签名消息""" signature = private_key.sign( message.encode(), padding.PSS( mgf=padding.MGF1(hashes.SHA256()), salt_length=padding.PSS.MAX_LENGTH ), hashes.SHA256() ) return signature def verify_signature(message, signature, public_key):
数字签名提供了不可否认性。如果签名者否认签名的消息,验证者可以使用公钥证明签名确实是由对应的私钥生成的。这在法律和商业场景中特别重要。
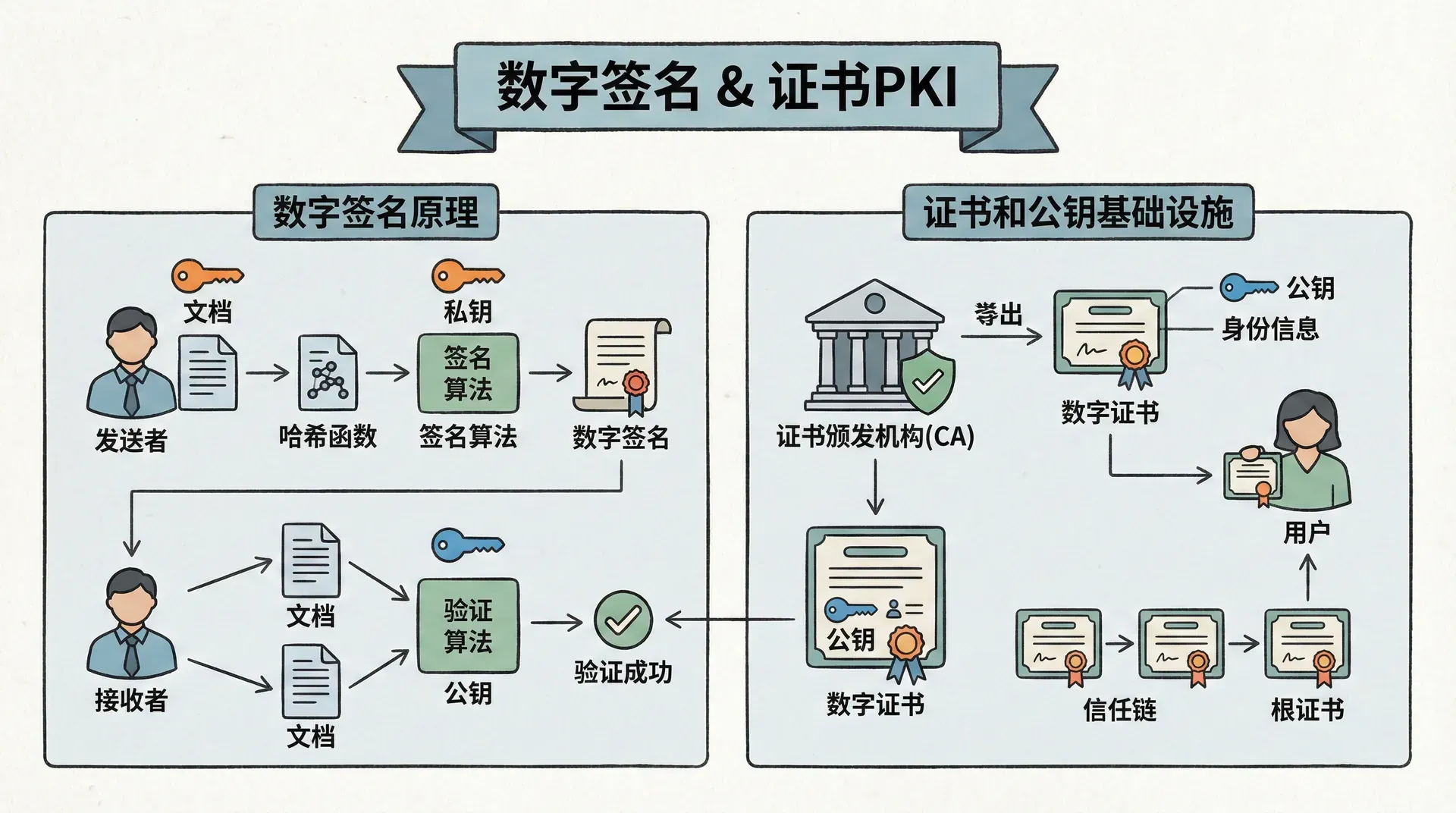
证书和公钥基础设施
在实际应用中,如何确保公钥的真实性是一个问题。攻击者可能提供伪造的公钥,声称是某个实体的公钥。这需要公钥基础设施(PKI)来解决。
PKI使用数字证书来绑定公钥和实体身份。证书由证书颁发机构(CA)签名,CA的公钥是预先信任的。通过验证证书链,可以确认公钥的真实性。
密钥管理
密钥管理是密码学中最薄弱的环节。许多安全漏洞不是由于加密算法的问题,而是由于密钥管理不当。
密钥生成
密钥必须使用密码学安全的随机数生成器生成。使用不安全的随机数生成器可能导致密钥可预测,从而被攻击者破解。
|import secrets # 使用secrets模块生成密码学安全的随机数 def generate_secure_key(length=32): """生成密码学安全的随机密钥""" return secrets.token_bytes(length) # 示例 key = generate_secure_key() print(f"密钥: {key.hex()}")
永远不要使用普通随机数生成器(如random模块)生成密钥。普通随机数生成器不是密码学安全的,生成的密钥可能被预测。应该使用secrets模块或cryptography库提供的随机数生成器。
密钥存储
密钥必须安全存储。永远不要将密钥硬编码在代码中,永远不要将密钥存储在版本控制系统中,永远不要将密钥通过不安全的渠道传输。
密钥存储的选项包括:
- 环境变量:适合开发环境,但不适合生产环境
- 密钥管理系统(KMS):如AWS KMS、Azure Key Vault
- 硬件安全模块(HSM):提供硬件级别的密钥保护
- 密钥派生:从主密钥派生子密钥,减少需要存储的密钥数量
密钥轮换
密钥应该定期轮换,限制密钥泄露的影响。即使攻击者获得了旧密钥,他们也只能解密使用旧密钥加密的数据,不能解密使用新密钥加密的数据。
密钥轮换需要仔细规划:
- 密钥版本管理:系统必须能够识别和使用不同版本的密钥
- 数据迁移:可能需要使用新密钥重新加密旧数据
- 向后兼容:在过渡期间,系统可能需要支持多个密钥版本
实际应用中的密码学陷阱
在实际应用中,密码学错误很常见, 常见的错误包括:
- 使用不安全的算法:使用MD5、SHA-1、DES等已经不再安全的算法。
- 密钥管理不当:硬编码密钥、在日志中记录密钥、通过不安全的渠道传输密钥。
- 实现错误:自己实现加密算法、使用错误的加密模式、不正确的IV使用。
- 侧信道攻击:实现可能泄露密钥信息,如通过执行时间、功耗、电磁辐射等。
- 协议错误:即使加密算法正确,协议设计错误也可能导致安全问题。
密码学实现非常困难,即使很小的错误也可能导致严重的安全漏洞。除非你是密码学专家,否则应该使用经过充分测试的密码学库,而不是自己实现。
总结
密码学是计算机安全的数学基础。对称加密提供高效的加密,非对称加密解决密钥分发问题,哈希函数提供数据完整性,MAC和数字签名提供消息认证和不可否认性。 但密码学不仅仅是数学理论,更是实际应用中的工程实践。密钥管理是密码学中最薄弱的环节,许多安全漏洞源于密钥管理不当。理解密码学的基本原理,以及如何在实践中正确使用密码学,是安全工程师的基本素养。
在下一个部分,我们将讨论安全协议。安全协议结合使用密码学技术来实现安全通信,如TLS、SSH等。理解这些协议的设计原理和潜在漏洞,对于理解现代网络安全至关重要。