数据库查询处理
当用户在数据库管理系统中提交一条SQL查询时,系统内部会启动一系列高度组织化的处理流程,将结构化查询语言转换为具体的数据访问操作,最终生成所需的查询结果。这一过程贯穿查询解析、优化、执行等多个阶段,确保查询高效、准确地完成。
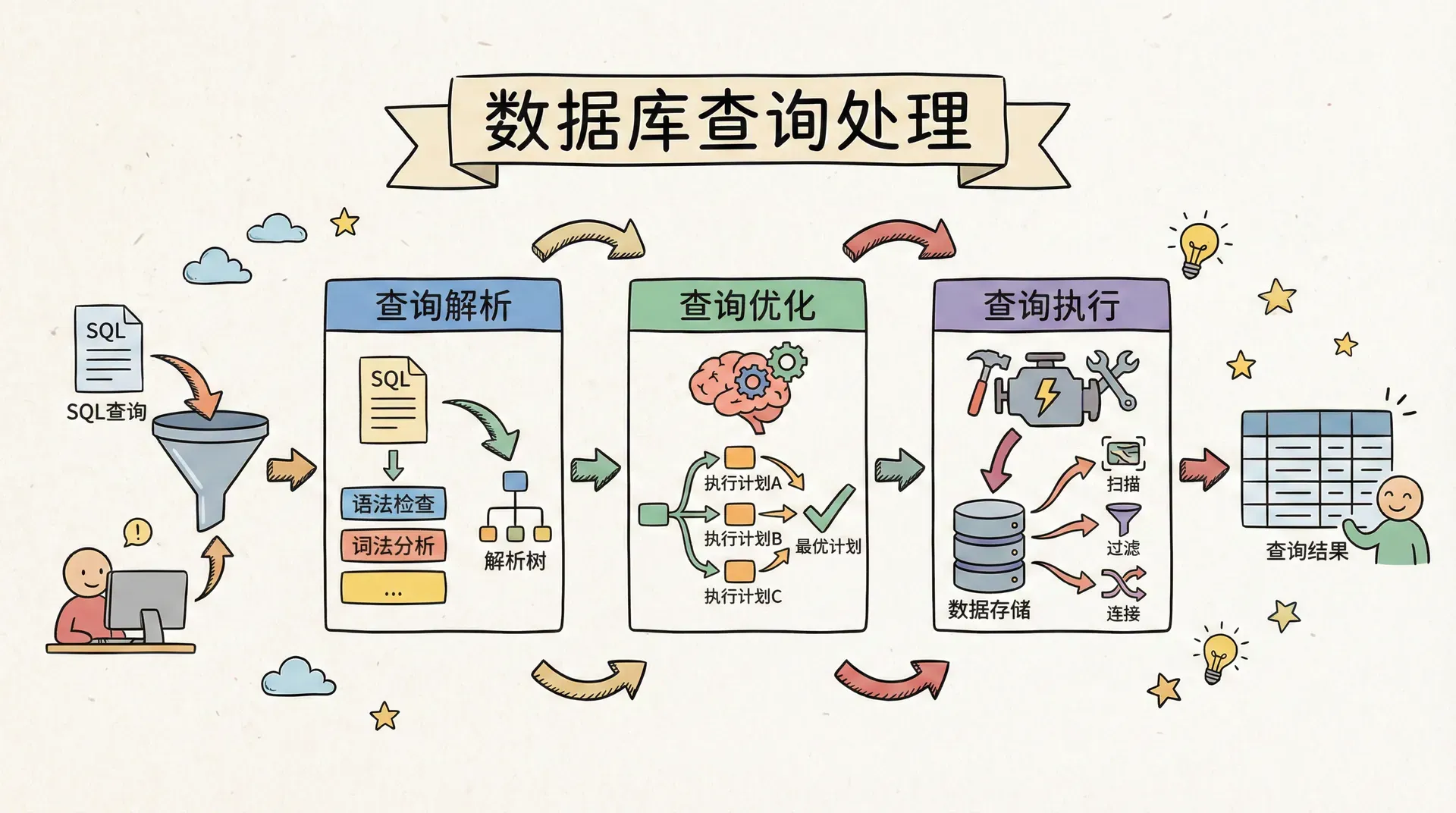
查询处理
查询处理是指数据库系统将用户提交的SQL查询语句转化为内部的数据检索操作,并最终生成查询结果的全过程。该过程涵盖查询的解析、优化和执行等多个阶段,旨在高效且准确地实现用户请求的数据访问。 数据库系统处理查询时,会经历三个主要阶段,每个阶段都有其特定的职责和任务。
当数据库收到一条SQL语句时,首先需要检查这条语句是否符合语法规范,就像语文老师检查作文的语法一样。系统会验证表名是否存在、列名是否正确、SQL语法是否合理等。
通过检查后,系统会将SQL语句转换为内部的关系代数表达式。关系代数是数据库理论中的数学语言,比SQL更适合计算机内部处理。
比如这样一条查询:
|SELECT 姓名 FROM 学生 WHERE 年龄 < 25;
会被转换为类似这样的关系代数表达式:
|π姓名(σ年龄<25(学生))
我们之前学过的,关系代数中的π表示投影(选择列),σ表示选择(筛选行)。
查询优化阶段是整个查询处理流程中最关键的环节,其核心目标是在多个可行的查询执行计划中,选择出预期代价最低的方案。查询优化器会基于代价模型,对各种物理执行计划进行枚举和评估,最终生成最优或近似最优的执行计划。
以“查找年龄小于25岁的学生姓名”为例,其执行方式可以有多种选择,例如:
- 全表扫描:遍历学生表的所有记录,逐条判断是否满足条件;
- 利用索引:若“年龄”字段存在索引,则可以通过索引快速定位到符合条件的记录,显著减少I/O开销。
优化器在做出决策时,会综合考虑关系表的规模、可用索引、数据分布统计信息及系统资源等因素,基于磁盘I/O、CPU代价、内存消耗等指标对各候选方案进行代价估算,从而选取整体成本最低的物理执行计划。
确定了最优的执行计划后,查询执行引擎就开始实际的数据检索工作。它会按照计划中指定的算法和顺序,一步步地从磁盘读取数据、处理数据,最终得到查询结果。
查询成本的度量
在数据库系统实现与优化过程中,亟需一种精确且可量化的方法对不同查询物理执行方案的优劣进行对比与评估——这便是查询成本度量模型的核心作用。其本质目标,是基于系统资源消耗和性能指标,为优化器在物理执行计划的选型过程中提供定量决策依据。
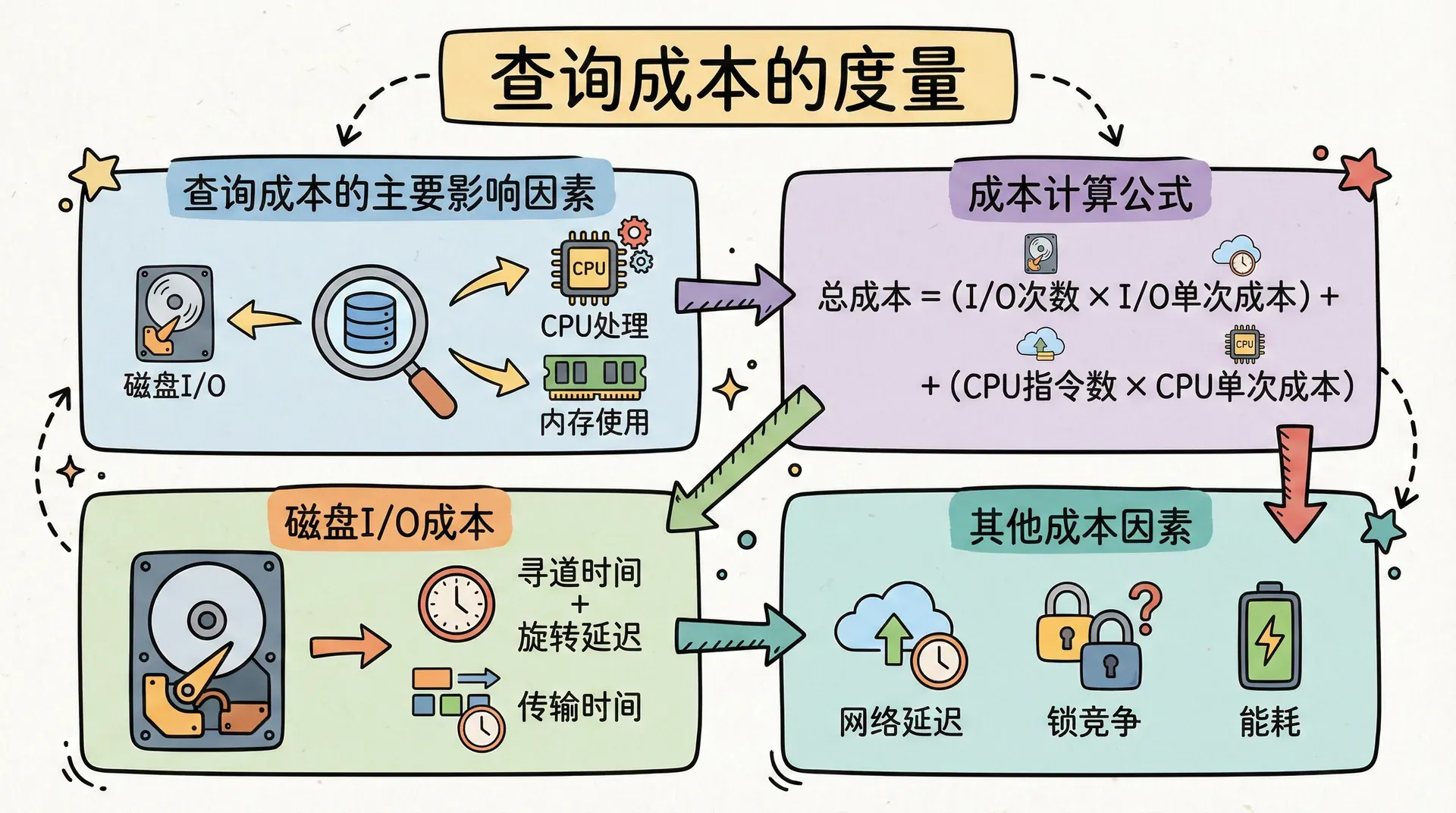
查询成本的主要影响因素
数据库查询成本综合体现了多种系统资源的消耗,其中磁盘I/O成本通常是影响最为显著的瓶颈,其次还包括CPU处理时间、内存占用、网络通信等。
磁盘I/O成本
在主流数据库系统中,外存(特别是机械硬盘)的数据访问速度远低于内存,I/O延迟常为CPU速度的数千倍。为严谨度量磁盘I/O成本,通常以以下两项系统参数为基础:
- 块传输时间 (tT):从磁盘顺序读取一个数据块(page/block)的平均耗时。
- 寻道时间 (tS):磁盘磁头定位到目标数据块所在柱面所需的平均物理寻道时延。
磁盘寻道时间普遍显著高于块传输时间。实际工程中,例如磁盘寻道平均需4毫秒,而4KB块传输时间仅约0.1毫秒。所以数据库优化目标常聚焦于降低寻道次数,以显著缩减I/O总体延迟。
成本计算公式
如果一个操作需要传输b个数据块,并进行S次磁盘寻道,那么总的执行时间为:
让我们看一个具体例子,假设我们有一个包含1000个数据块的表,需要全表扫描:
- 如果按顺序读取:需要1次寻道 + 1000次块传输 = 1 × 4ms + 1000 × 0.1ms = 104ms
- 如果随机读取:需要1000次寻道 + 1000次块传输 = 1000 × 4ms + 1000 × 0.1ms = 4100ms
我们可以看出,顺序访问比随机访问快了将近40倍!
其他成本因素
现实中实际的成本估算面临许多复杂因素:
因此,数据库优化器通常采用相对简化的成本模型,重点关注磁盘访问成本,并通过统计信息来提高估算准确性。
选择操作的实现策略
选择操作(Selection, σ)是关系数据库中最基本且最频繁使用的操作之一,其本质是在给定的关系表中,根据用户指定的谓词条件,高效筛选出所有满足该条件的元组(记录)。该操作直接影响后续查询处理的性能与资源消耗,是查询优化的核心基础。
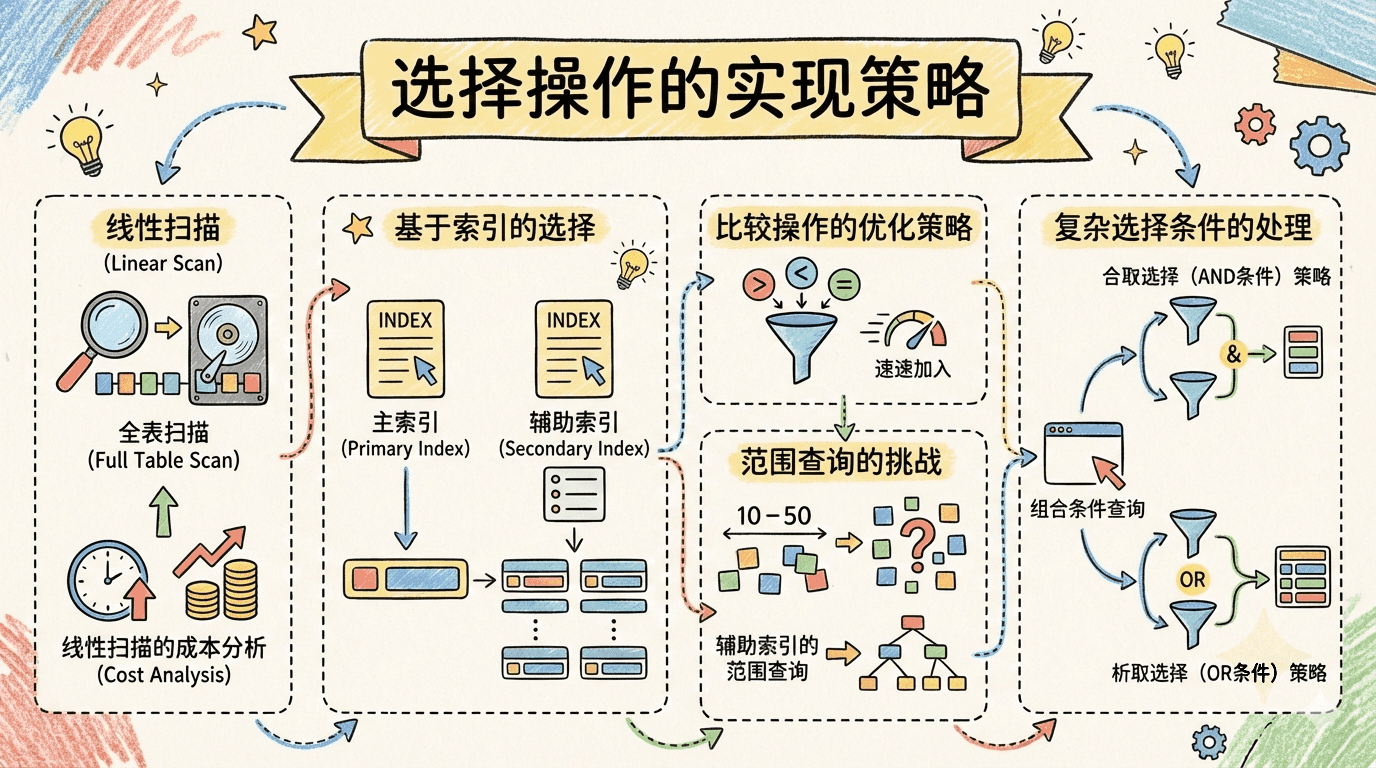
比如这样的查询:
|SELECT * FROM 员工表 WHERE 工资 < 8000;
这个查询的选择操作就是找出所有工资低于8000元的员工记录。
线性扫描
全表扫描
线性扫描(Linear Scan,或称顺序扫描)是实现选择(Selection)操作最基础、最通用的方法。它的核心思想为:自表的起始数据块依次顺序读取每一个磁盘块,对块内的每条元组进行谓词判断,将满足条件的元组输出到结果集。该策略不依赖任何索引结构或数据排序,适用于任意选择谓词。
以在包含10万名员工记录的关系表中执行“工资 < 8000”的查询为例,其具体步骤如下:
- 依次顺序读取全部存储员工数据的数据块
- 针对每个被读取的块,对块内所有元组逐一进行谓词"工资 < 8000"的布尔判断
- 若元组满足选择条件,则将其加入结果集
线性扫描的成本分析
以员工表为例,假设:
- 表包含1000个数据块
- 平均每个块包含100条员工记录
最坏情况成本:需要扫描整个表
平均情况成本:如果查找的是唯一值(如员工编号),平均只需扫描一半的数据
线性扫描虽然简单,但它有一个重要优势:适用于任何查询条件,不依赖索引或特定的数据组织方式。当表很小或者需要检索大部分数据时,线性扫描往往是最高效的选择。
基于索引的选择
主索引
主索引是指按照某一关键字段(通常为主键)对表中数据的物理存储顺序进行组织的数据结构。主索引结构(如B+树)不仅承担高效检索的任务,还要求数据记录本身在物理上顺序排列,与主索引键的排序保持一致。这一特性通常称为“聚簇”(Clustered)。 以员工表为例,若主索引建立在“员工编号”字段上,则数据文件中所有记录均按员工编号递增的顺序有序排列,方便范围查询与顺序访问操作的高效执行:
等值查找示例:
|SELECT * FROM 员工表 WHERE 员工编号 = 'E001234';
使用主索引查找特定员工编号的流程如下:
在B+树索引中查找'E001234'
索引指向包含该记录的数据块
读取该数据块获取完整记录
如果B+树有4层,那么我们的总成本就是5次磁盘访问。
辅助索引
辅助索引(Secondary Index)是一种为表中非主属性(非主键)字段建立的索引结构,旨在加速基于该字段的检索操作。不同于主索引,辅助索引的数据记录在物理存储上未必按照索引键的顺序排列,因此通过辅助索引定位到目标索引项后,需额外访问对应的数据块以获取完整记录。
|SELECT * FROM 员工表 WHERE 部门 = '技术部';
如果部门字段上有辅助索引:
在部门索引中查找'技术部'
获得所有技术部员工的记录地址列表
根据地址逐一读取员工记录
辅助索引的成本可能很高,因为每个匹配的记录可能分布在不同的数据块中。如果技术部有1000名员工,且他们的记录分散在1000个不同的数据块中,就需要:
当辅助索引返回大量记录时,其成本可能超过线性扫描。这就是为什么数据库优化器需要根据数据分布统计信息来选择最优策略。
比较操作的优化策略
范围查询的挑战
比较操作(如 <、>、>=、<= )比等值查询更复杂,因为它们涉及一个值的范围。
|SELECT * FROM 员工表 WHERE 工资 >= 10000 AND 工资 <= 20000;
如果工资字段有主索引,处理工资范围查询的步骤如下:
在索引中定位到工资为10000的第一条记录
从该位置开始顺序扫描,直到工资超过20000的第一条记录
由于是主索引,满足条件的记录在物理存储中是连续的
其中b是包含结果记录的数据块数量,由于记录连续存储,只需要少量的寻道操作。
辅助索引的范围查询
使用辅助索引处理范围查询时,情况变得复杂,其步骤如下:
在索引的叶子层扫描范围内的所有条目
对每个索引条目,访问对应的数据记录
由于记录可能分散存储,每次访问都可能需要寻道
对于选择性很高的查询(返回少量记录),辅助索引很有效。但对于选择性较低的查询(返回大量记录),线性扫描可能更高效。
复杂选择条件的处理
组合条件查询
实际数据库查询通常涉及多个选择条件,这些条件通过逻辑连接符(如 AND、OR、NOT)组合形成复杂的复合查询。
|SELECT * FROM 员工表 WHERE 部门 = '技术部' AND 工资 > 8000 AND 工作年限 >= 3;
合取选择(AND条件)策略
对于包含多个AND条件的查询,有几种处理策略,比如:
策略一:单索引过滤
- 选择最具选择性的条件使用索引
- 对返回的记录在内存中检查其他条件
比如先用部门索引找到所有技术部员工,然后在内存中过滤工资和工作年限条件。
策略二:复合索引 如果存在包含多个字段的复合索引,可以直接使用:
|-- 如果存在(部门, 工资, 工作年限)复合索引 CREATE INDEX idx_complex ON 员工表(部门, 工资, 工作年限);
策略三:索引交集
- 分别使用各个条件的索引获得记录ID列表
- 计算这些列表的交集
- 根据交集中的ID读取实际记录
析取选择(OR条件)策略
OR条件的处理则更具挑战性:
|SELECT * FROM 员工表 WHERE 部门 = '技术部' OR 工资 > 15000;
策略:索引联合
- 针对每个 OR 条件分别利用可用索引扫描,获取满足各条件的记录ID集合(如RowID或主键)。
- 对各条件返回的记录ID集合执行并集运算,去除重复ID,合并为最终候选结果集。
- 根据合并后的ID集合访问表数据,读取满足任一条件的最终记录。
注意事项:
- 若所有OR条件均有可用索引,索引联合可极大提升查询效率,避免全表扫描。
- 若存在任一条件无法利用索引(需全表扫描),则通常数据库优化器会选择对全表进行顺序扫描,以避免多次随机I/O,提升整体性能。
不同选择策略的适用场景:
选择最优策略的关键是准确估计各种方法的成本。现代数据库系统会维护详细的统计信息,包括表大小、索引选择性、数据分布等,以帮助优化器做出最佳决策。
排序操作与外部排序
排序在数据库系统中具有重要且多层次的作用。一方面,排序操作使用户能够获得按照特定属性(如工资降序等)有序的查询结果。另一方面,排序还是数据库实现高效连接(如merge join等)、去重、分组、窗口函数等复杂操作的基础。高效的排序直接影响整体查询性能和内部算子的执行效率。
在实际应用中,排序处理方式主要分为“内存排序”和“外部排序”两大类,具体取决于待排序数据集与系统可用内存的关系。
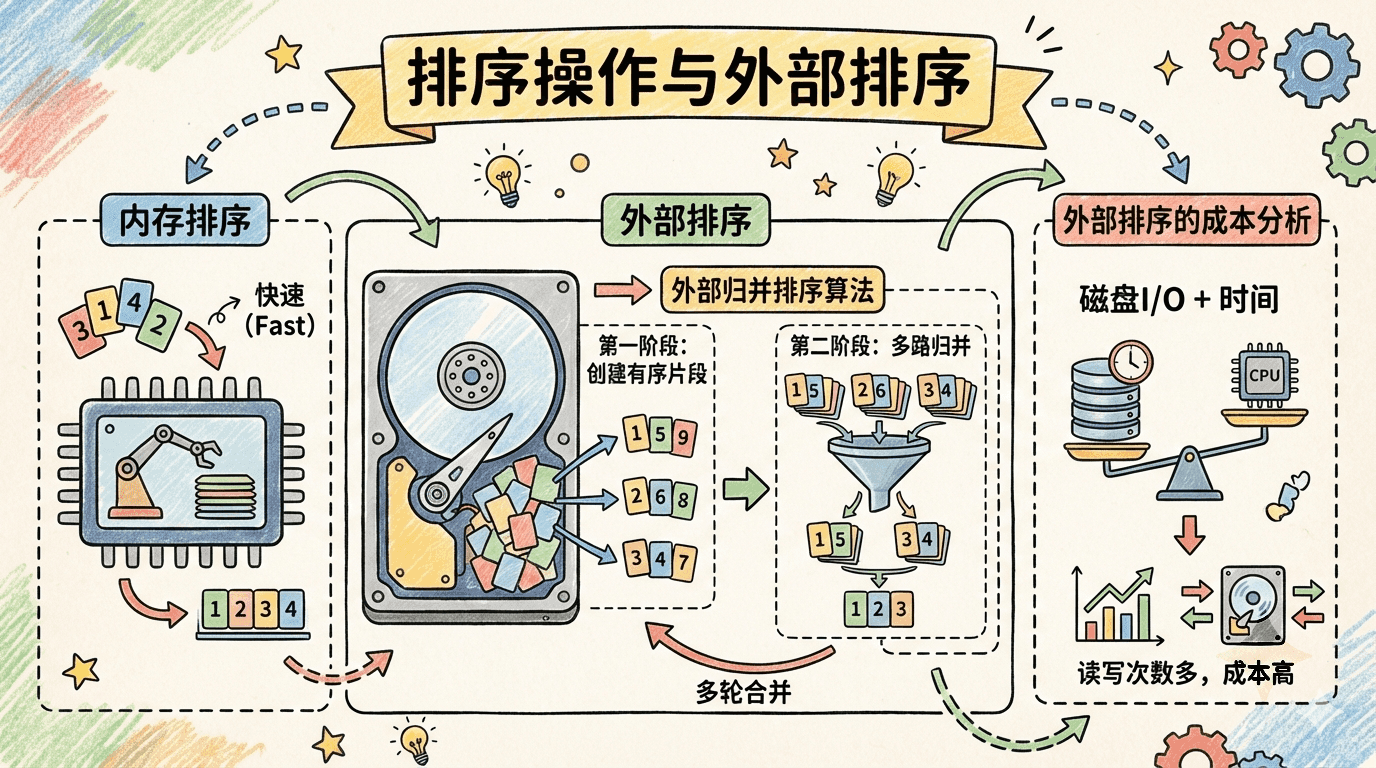
内存排序
当待排序的数据量能够完全被装载进内存时,数据库系统会采用传统的内存排序算法(如快速排序、堆排序等)。内存排序通常具有 O(n log n) 的时间复杂度,对中小规模数据排序极为高效。
然而,现实的业务数据往往存储在大表中,记录总量可能达数百万、数千万甚至数十亿行,其整体体积远超主机物理内存容量。在这种场景下,直接采用内存排序不仅无法完成任务,还会因频繁的内存溢出和磁盘交换导致性能急剧下降。
外部排序
为应对超大规模数据集的排序需求,数据库系统采用“外部排序”方法。外部排序的核心思想是利用有限的内存将整体排序任务分解为多个可以分别处理的小规模子任务,充分协调磁盘与内存资源,以实现全局有序输出。
这一策略的本质,即“分治”:先分别对能够装入内存的小数据块排序,再借助高效的归并算法,多轮合并成全局有序结果。以此方式,数据库可以完成大规模数据集的全表排序、关联表按键排序等关键操作。
外部归并排序算法
外部归并排序(External Merge Sort)是关系数据库系统中最常用的外部排序算法,具备良好的IO亲和性和可扩展性。该算法主要包含两个阶段:
- 分段(Run Generation):将整个大数据集切分为内存可承载的子集,分别加载到内存中使用高效算法完成排序,并将每个有序子集(称为“初始归并段”)写回磁盘,形成临时排序文件。
- 多路归并(Multi-way Merge):利用有限的内存缓冲,从多个有序子文件中批量读取数据,通过优先队列或堆结构选出最小项,逐步合并生成更大规模的有序文件,最终得到全局有序输出。
这种分阶段排序/归并策略大大降低了I/O开销,并能够处理超大体量的关系数据集,是数据库面向大表查询时排序操作的核心实现机制。
第一阶段:创建有序片段
设有一个由1000个数据块组成的员工表,且系统可用内存容量为10个数据块,外部排序的第一阶段的步骤如下:
- 每次从磁盘顺序读取10个数据块数据,加载至内存缓冲区;
- 针对加载的块内记录采用高效内存内排序算法(如快速排序、堆排序等)完成内部排序;
- 将排序后的10个数据块作为一个初始归并段(run)写回磁盘,形成一个临时有序文件(如 R₀);
- 重复上述过程,不断读取接下来的10个数据块、排序、写盘,直至整个表内所有数据块均被处理。
最终结果:共生成100个初始有序归并段(1000 ÷ 10 = 100),每个段均包含10个数据块,且段内数据已排好序。
第二阶段:多路归并
现在我们需要将100个有序文件合并成一个完全有序的文件。
归并过程:
- 为每个初始归并段(临时有序文件)分配一个独立的输入缓冲区(通常为1个数据块大小)。
- 分配一个用于存放归并结果的输出缓冲区。
- 初始化时,从每个输入文件读取首个数据块加载至各自的输入缓冲区。
- 利用最小堆(或优先队列)比较所有输入缓冲区中的当前最小记录,选取全局最小元素。
- 将选中的最小记录写入输出缓冲区,输出缓冲区满时批量写回磁盘。
- 从产生该最小记录的输入缓冲区所在文件读取下一条(如当前块已读完则加载下一个块,若文件耗尽则不再参与比较)。
- 重复执行步骤4-6,直至所有输入缓冲区和输入文件均处理完成,最终获得全局有序文件。
多轮合并
在上面的例子中,我们有100个临时文件,但内存只能容纳10个缓冲区。这意味着我们无法在一轮中完成所有文件的合并,所以我们需要进行多轮合并:
第一轮:每次合并9个文件(为输出预留1个缓冲区),100÷9≈12轮,产生12个更大的有序文件
第二轮:合并这12个文件,由于12<9,可以一次完成
外部排序的成本分析
- br:待排序的总数据块数
- M:可用内存块数
- logₘ₋₁(br / M):按每轮可归并M-1路计算的合并轮数(上取整)
外部排序的I/O成本主要由所有读写磁盘操作构成,通常以“块传输次数”衡量,其计算分为两个阶段:
初始归并段划分阶段(分割阶段):顺序读入全部原始数据(br 次块传输),将已排序的初始归并段写回磁盘(br 次块传输),共计 2br 次块传输。
多路归并阶段:设归并过程需要进行 p 轮,每轮都需完整读写全部数据,每轮 I/O 成本为 2br 次块传输,因此总合并阶段成本为 2br × p。但实际上最后一轮归并结果只需读入,不需写回,因此最终精确成本为 2br × (p-1) + br。
外部排序总I/O成本公式(块传输总次数):
以排序一个包含1000块数据、内存大小为10块的情况为例,首先在分割阶段将1000块数据分为每块10块的100个临时文件,产生的块传输成本为2 × 1000 = 2000次。随后进入合并阶段,每轮最多合并9个文件(M-1=9),需要log₉(100) ≈ 2.1,向上取整为3轮,合并阶段的块传输成本为2000 × (3-1) + 1000 = 5000次。 最终,总成本为2000 + 5000 = 7000次块传输。
外部排序的效率很大程度上取决于可用内存的大小。内存越大,需要的合并轮数就越少,总体性能就越好。这就是为什么现代数据库系统在进行大规模排序操作时会尽可能分配更多的内存缓冲区。
连接操作
在实际业务中,分布于不同表的相关实体信息通常依赖连接操作进行有效整合。例如,学生基本信息保存在“学生”表,课程选修及成绩记录存储于“选课”表,而要获得“某学生选修的所有课程及成绩”等数据,须通过学生ID等外键进行等值连接。
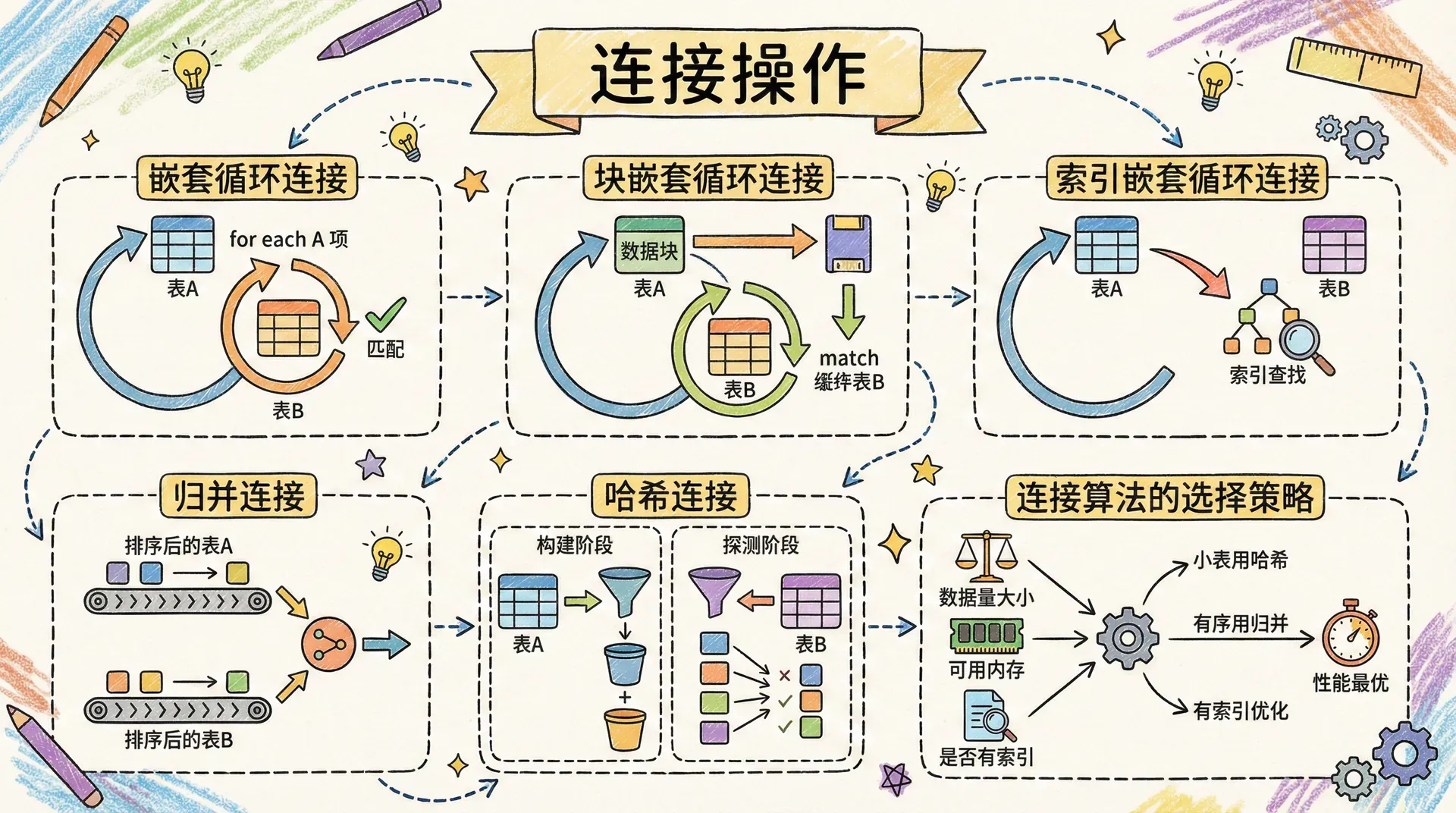
连接操作在数据库查询处理过程中通常是主要的性能瓶颈,尤其对于大规模数据集。其原因在于连接涉及两个关系间所有可能的记录对的判定,计算量为两个表记录数的乘积(即笛卡尔积的筛选),在数据量较大时会产生海量的比较操作。 因此,关系型数据库系统在执行连接时会优先考虑合适的连接算法和访问策略,以提高查询效率、减少I/O成本。
为了便于理解各种连接算法,我们设定一个具体的例子:
学生表(Students):
- 基本元组数(Cardinality):5000
- 存储所占块数:100(假设每块可容纳若干学生记录)
- 典型字段:学生ID(主码)、姓名、专业
选课表(Enrollments):
- 基本元组数:10000
- 存储所占块数:400
- 典型字段:学生ID(外键,参照学生表)、课程ID、成绩
目标连接查询:
|SELECT 学生.姓名, 学生.专业, 选课.课程ID, 选课.成绩 FROM 学生 JOIN 选课 ON 学生.学生ID = 选课.学生ID;
嵌套循环连接
嵌套循环连接(Nested Loop Join)是一种基础的关系型数据库连接算法。其实现方式是在外表(驱动表)上逐个扫描每一条元组,对于每个外表元组,都对内表进行一次全表扫描,依次比较内外表当前元组是否满足连接条件,若满足则输出结果。该方法本质上对应两个嵌套的迭代(循环),其时间复杂度与两个输入关系的记录数乘积成正比。
在上述示例下,嵌套循环连接的具体执行流程如下:
- 从学生表(外表)中依次读取每一条学生记录(例如,学号为 S001 的张三)。
- 针对当前学生记录,对选课表(内表)进行全表扫描,筛选出所有学生ID等于 S001 的选课记录。
- 对于每一条匹配的选课记录,生成并输出对应的连接结果元组。
- 重复上述过程,直到学生表中所有记录均处理完毕。
嵌套循环连接(Nested Loop Join)的I/O成本高度依赖于参与连接的两个关系的基数与物理占用的块数,其开销量级直接由存取模式决定:
最差情况下的I/O成本(假设可用缓冲区极小,仅能容纳一条外表记录和一页内表):
- 外表(学生表)每读取一条元组均需对内表(选课表)做一次全表扫描
- 总块传输次数(Block Transfer):
- 外表:100(完整扫描一次)
- 内表:5000 × 400(每条学生记录,扫描一次400块的选课表)
- 总计 = 100 + 2,000,000 = 2,000,100 次
- 磁盘寻道次数(Seek/Rotation):
- 外表:100(块数)
- 内表:5000(每条外表元组,对内表表头寻道)
- 总计 = 100 + 5,000 = 5,100 次
最佳情况下的I/O成本(假设全部数据能缓存在内存中):
- 仅需分别全表扫描各1次
- 总块传输次数 = 100(学生表)+ 400(选课表)= 500 次
- 磁盘寻道次数 = 2 次(外表、内表各1次)
嵌套循环连接的成本可能非常高,特别是当两个表都很大时。在我们的例子中,最坏情况需要超过200万次块传输!这就是为什么选择正确的外表很重要——应该选择较小的表作为外表。
块嵌套循环连接
传统嵌套循环连接的主要性能瓶颈在于,每处理一条外表记录都需要对内表执行一次全表扫描,导致I/O次数随外表记录数线性增加。块嵌套循环连接对此进行了优化: 以外表的数据块(而非单条记录)为处理单位,每次将一整个外表块缓冲入内存,与内表全表进行连接操作。这样每个外表块只需引发一次对内表的全表扫描,从而显著降低了对内表的I/O访问次数,提高整体连接效率。
- 依次读取学生表的一个数据块(每块约含50条学生元组)进入缓冲区;
- 对内表(选课表)进行一次全表扫描,将扫描到的选课记录与当前缓冲区中的所有学生元组进行连接匹配,生成连接结果;
- 继续读取下一个学生表数据块,并重复步骤2,直到外表(学生表)所有数据块均处理完毕。
块嵌套循环连接(Block Nested Loop Join, BNLJ)的I/O代价分析:
-
总块传输次数(Block Transfer):
总I/O = 读外表一次 + 外表每个数据块全扫描内表一次
= 100(学生表块数) + 100 × 400(每个学生表块扫描全部内表块)
= 40,100 次 -
总寻道/旋转次数(Seek/Rotation):
假定每处理一个外表块都需2次寻道(定位外表块和内表表头),则
= 100 × 2 = 200 次
相比传统嵌套循环连接的2,000,100次块传输,I/O成本显著降低,体现出块粒度处理带来的巨大性能提升。
缓冲区管理与多块加载策略:若内存缓冲区可容纳M个块,则可采用如下策略以进一步优化I/O:
- 一次性加载 M-2 个外表数据块进入内存;
- 分别保留1个块用于内表输入预读与1个块用于结果输出缓存。
此时,内表需要被顺序扫描 ⌈外表块数 / (M-2)⌉ 次,进一步摊薄内表I/O。例如,若M=12,则每5个外表块仅需扫描内表一次,大幅减少总I/O代价。
内表交替扫描(Double-Scan)优化:对于顺序磁盘布局的内表块,可以通过交替正、反方向扫描(Alternating Scan),充分利用预读机制及缓冲空间,从而降低寻道和旋转延迟,提高I/O吞吐率。该策略在多次扫描内表场景下尤其有效,有助于提升整体连接效率。
索引嵌套循环连接
当内表在连接列上建立了索引(如B+树索引)时,索引嵌套循环连接可以利用索引高效定位匹配元组,无需对内表进行全表扫描。对于每一条外表记录,系统根据连接键通过索引执行一次快速查找,仅访问与该记录关联的内表元组,极大减少了I/O操作。
索引嵌套循环连接的I/O成本分析:对于每一条外表(学生表)记录,都需要通过内表(选课表)的B+树索引(假设高度为4且内表已在连接属性上建好索引)来查找匹配元组。 以5000条学生记录为例,每次查找通常需要4次磁盘I/O(对应B+树从根到叶节点),并且每条记录还要多一次I/O读取匹配的数据块。因此,每一次连接的I/O成本等于索引查找的I/O次数与实际匹配块的读取I/O之和。
详细成本估算(设平均每位学生选修2门课程):外表(学生表)全表扫描需要读取100个数据块,索引检索时每条学生记录需4次块传输(共5000 × 4 = 20,000次),匹配的数据读取共需5000 × 2 = 10,000次(假设每条匹配记录都需一次I/O)。因此,总I/O成本为100(学生表扫描)+20,000(索引检索)+10,000(读取匹配记录)= 30,100次块传输。
需要注意的是,若选课表连接列上存在大量匹配(高基数关联)且匹配记录分布离散,实际I/O成本可能进一步上升,部分情况下反而不如块嵌套循环连接。只有当索引选择性较高时,该方法才具有明显性能优势。
索引嵌套循环连接适用于连接结果相对较少的情况。如果连接会产生大量结果,块嵌套循环连接可能更高效。这就是查询优化器需要根据统计信息来做决策的原因。
归并连接
归并连接(Merge Join)要求连接操作涉及的两个输入关系在连接属性上均为已排序状态。如果输入表未按连接字段排序,则需首先对两个表分别进行外部排序,以确保数据有序,从而为高效归并打下基础。
该算法的核心思想与归并排序的合并过程相似。归并连接通过分别维护两个输入表在连接属性上的游标(或读取指针),每次比较当前指向的记录,根据连接属性值推进相应的游标,实现两个数据流的顺序扫描与同步处理。
假定连接的两个输入关系R(学生表)和S(选课表)均已按照连接属性(如StudentID)升序排序,归并连接的过程如下:
-
输入关系示例
- 学生表(R):S001(张三)、S003(李四)、S005(王五)……
- 选课表(S):S001(数学)、S001(英语)、S003(物理)、S005(化学)、S005(生物)……
-
归并连接算法步骤
- 初始化两个游标(scan pointer),分别指向R和S的首个元组。
- 比较当前两个元组的连接键(StudentID):
- 若R.StudentID = S.StudentID,则产生连接结果,将两个游标均向前推进,或根据实际需求对S中重复键进行批处理。
- 若R.StudentID < S.StudentID,则R游标前移。
- 若R.StudentID > S.StudentID,则S游标前移。
- 重复步骤2,直至某一输入扫描结束。
归并连接的I/O成本分析(假设输入已排序):R表和S表各进行一次顺序全表扫描,I/O成本为100(R表块数)+ 400(S表块数)= 500次块传输。由于为顺序访问,磁盘寻道和转动延迟极低,I/O效率最优。
考虑排序操作的总体成本:若输入尚未按照连接属性排序,则需先对两表执行外部排序。总体I/O成本=两表排序成本+连接过程I/O。根据外部排序的I/O公式,实际总成本通常仍优于索引嵌套循环连接和块嵌套循环连接,尤其在处理大规模数据时表现更为出色。
在三大传统连接算法中,归并连接(对于已排序输入)通常具有最低的I/O开销。归并连接是最高效的连接算法之一,特别适用于大型表的连接。即使需要预先排序,其总体成本往往也比其他方法更低。这就是为什么许多数据库系统会选择先排序再连接的策略。
哈希连接
哈希连接是一种基于哈希分区思想实现的高效等值连接算法。该算法首先对两个输入关系(如学生表与选课表)分别按照连接属性应用同一个哈希函数进行分区,将具有相同哈希值(即连接键等值)的元组映射到同一个分区。 分区后,只需对对应分区进行连接,可以大幅减少无关数据的比较和I/O开销。由于只有哈希值相等的记录才有可能匹配,极大地提升了连接操作的效率。
哈希连接的本质特点是将大规模连接转化为多个较小子问题,充分利用内存哈希表进行快速匹配。该算法适用于连接字段分布均匀、没有排序要求且无法有效利用索引的场景,尤其在处理大数据集时相较于嵌套循环连接具有明显的性能优势。
**阶段一:分区 **
- 选定适用于连接键(如StudentID)的哈希函数 h,将所有输入关系(如学生表R和选课表S)的记录根据连接字段进行哈希映射,分散至若干磁盘分区(buckets)。
- 遍历学生表R,将每一元组以 h(R.StudentID) 的哈希值写入对应的R子分区。
- 遍历选课表S,采用完全相同的哈希函数,将每一元组以 h(S.StudentID) 的哈希值写入对应的S子分区。
- 分区操作完成后,所有连接键相同的元组组必然被分配至同一编号的分区内,分区数据通常存储为临时外部文件,供下一阶段读入。
阶段二:连接,对于每对编号相同的R、S分区,执行以下操作:
- 选择其中数据量较小的分区(通常为学生表子分区),将其整体装载至内存,基于连接字段建立高效的内存哈希表结构。
- 顺序读取对应S分区中的每一元组,利用哈希表以连接字段为关键字进行高效查找,匹配所有可连接元组。
- 对于成功匹配的元组对,直接输出为连接结果,或根据业务需求拼接输出全部连接属性。
假设采用哈希函数 h(StudentID) = StudentID % 3,对学生表进行3路分区:
- 学生记录 S001:h(S001) = 1,映射至分区1
- 学生记录 S002:h(S002) = 2,映射至分区2
- 学生记录 S003:h(S003) = 0,映射至分区0
哈希连接的I/O成本主要分为分区阶段和连接阶段。分区阶段,需要顺序读取两个输入表(如学生表和选课表),共计100 + 400 = 500次块传输,并将数据根据哈希函数写入各自的分区文件,再次产生100 + 400 = 500次块传输,总计1000次块传输。连接阶段,对于每对编号相同的分区,每个分区需从磁盘读入,共计100 + 400 = 500次块传输。因此,哈希连接的总体I/O成本为1500次块传输,显著低于传统嵌套循环连接算法。
分区数量的合理确定:为确保哈希连接过程中每个分区的较小输入端(即“构建表”)能够被完整装载至内存,分区数量应满足 ,其中 为构建表的块数, 表示可用内存的块数。例如,若学生表占用100个块而内存仅可容纳个块,则分区数至少为,以保证每个分区最大的数据量不超过内存上限。
递归分区策略:若某些分区划分后仍大于内存容量,则需对其递归应用分区过程,即:
- 针对溢出分区,选择不同的哈希函数进行再次分区,将其进一步拆分;
- 按需多次递归,直至所有产生的子分区均能被独立加载进可用内存,从而完成后续连接阶段。
混合哈希连接优化:如可用内存较为充足,可采用混合哈希连接技术,将部分分区(如分区0)永久驻留于内存,无需中间写盘与后续读盘,从而减少I/O成本,提高整体连接效率。
连接算法的选择策略
实战练习
习题1:选择操作优化
假设有一个员工表(employees),包含以下字段:
- emp_id (员工编号,主键)
- name (姓名)
- department (部门)
- salary (工资)
- hire_date (入职日期)
请分析以下查询使用哪种选择策略最优,并解释原因:
|SELECT * FROM employees WHERE department = '技术部';
|答案:使用辅助索引策略 如果department字段上有辅助索引,可以通过索引快速定位技术部员工的记录位置,然后直接访问这些记录。 如果没有索引,则需要使用线性扫描遍历整个表。 成本分析:索引策略成本 ≈ 索引查找成本 + 匹配记录读取成本
习题2:范围查询成本计算
使用同一个员工表,假设表有1000个数据块,工资字段上有主索引。请计算以下查询的I/O成本:
|SELECT * FROM employees WHERE salary BETWEEN 50000 AND 100000;
|答案:使用主索引范围查询 假设工资字段是主索引,记录按工资升序排列: - 索引定位到第一个salary >= 50000的记录:约3-4次磁盘访问(B+树高度) - 顺序读取满足条件的连续记录块:假设结果占50个数据块 - 总成本 ≈ 4 + 50 = 54次磁盘访问 如果使用辅助索引,需要读取每个匹配记录,可能需要50+次随机访问,成本更高
习题3:复杂条件查询优化
员工表增加一个字段:performance_rating (绩效等级,1-5分)。请分析以下查询的处理策略:
|SELECT * FROM employees WHERE department = '技术部' AND salary > 80000 AND performance_rating >= 4;
|答案:可以使用索引交集策略 1. 使用department索引找到技术部员工ID列表 2. 使用salary索引找到工资>80000的员工ID列表 3. 使用performance_rating索引找到绩效>=4的员工ID列表 4. 计算三个列表的交集,得到满足所有条件的员工ID 5. 根据ID读取最终记录 如果存在复合索引(department, salary, performance_rating),可以直接使用该索引一次查找。
习题4:外部排序成本计算
假设需要对员工表按工资排序,表有10000个数据块,系统可用内存为100个数据块。计算外部排序的总I/O成本。
|答案:使用外部归并排序 第一阶段(创建有序片段): - 每次读100个块到内存,排序后写回:10000 × 2 = 20000次块传输 第二阶段(多路归并): - 初始片段数:10000 ÷ 100 = 100个片段 - 每轮可合并99个片段(内存中99个输入缓冲区+1个输出缓冲区) - 合并轮数:log₉₉(100) ≈ 1轮 - 合并阶段:100 × 2 = 200次块传输(读写各一次,最后一轮只需读) 总成本 = 20000 + 200
习题5:连接算法选择
有以下两个表:
学生表(students):
- student_id (学生编号,主键)
- name (姓名)
- major (专业)
- gpa (平均成绩)
选课表(enrollments):
- student_id (学生编号,外键)
- course_id (课程编号)
- grade (成绩)
- semester (学期)
请分析以下查询应使用哪种连接算法最优:
|SELECT s.name, s.major, e.course_id, e.grade FROM students s JOIN enrollments e ON s.student_id = e.student_id WHERE s.gpa > 3.5;
|答案:推荐使用索引嵌套循环连接 1. 先从students表选择gpa > 3.5的学生(假设有索引,筛选出少量高分学生) 2. 对于每个筛选出的学生,使用enrollments表上的student_id索引查找该学生的选课记录 3. 连接结果相对较少,索引查找效率高 如果两个表都很大且无合适索引,可以考虑哈希连接或归并连接。
习题6:哈希连接分区计算
继续使用上面的学生表和选课表,假设:
- students表:5000条记录,100个数据块
- enrollments表:20000条记录,400个数据块
- 可用内存:50个数据块
计算哈希连接的I/O成本。
|答案:哈希连接成本分析 第一阶段(分区): - 读两个表:100 + 400 = 500次块传输 - 写分区文件:100 + 400 = 500次块传输 - 分区阶段总计:1000次块传输 第二阶段(连接): - 读回所有分区进行连接:100 + 400 = 500次块传输 总I/O成本:1000 + 500 = 1500次块传输 分区数量确定:为确保构建表(通常选择较小的students表)能放入内存, 分区数至少为 ceil(100/
习题7:查询优化策略比较
使用员工表,比较以下两种查询的处理策略:
查询A:
|SELECT * FROM employees WHERE emp_id = 12345;
查询B:
|SELECT * FROM employees WHERE salary > 100000;
|答案: 查询A(等值查询,主键): - 最佳策略:主索引查找 - 成本:B+树高度(通常3-4次磁盘访问)+ 1次数据块读取 - 总成本约4-5次磁盘访问 查询B(范围查询,高选择性): - 策略1:辅助索引(如果salary有索引)+ 记录读取 - 策略2:线性扫描(如果选择性很高,可能更高效) - 成本取决于结果集大小和索引选择性 优化器会根据统计信息选择最优策略。
习题8:多表连接顺序优化
有三个表:
部门表(departments):
- dept_id (部门编号,主键)
- dept_name (部门名称)
- location (位置)
员工表(employees):
- emp_id (员工编号,主键)
- name (姓名)
- dept_id (部门编号,外键)
- salary (工资)
项目表(projects):
- project_id (项目编号,主键)
- project_name (项目名称)
- dept_id (负责部门,外键)
请分析以下查询的连接顺序:
|SELECT e.name, d.dept_name, p.project_name FROM employees e JOIN departments d ON e.dept_id = d.dept_id JOIN projects p ON d.dept_id = p.dept_id WHERE e.salary > 50000;
|答案:推荐连接顺序:employees → departments → projects 1. 先从employees表选择salary > 50000的员工(减少后续处理的数据量) 2. 将筛选结果与departments表连接,获取部门信息 3. 最后与projects表连接,获取项目信息 这样可以尽早应用选择条件,减少中间结果的大小。 如果有合适的索引,可以考虑使用索引嵌套循环连接。