受限因变量模型

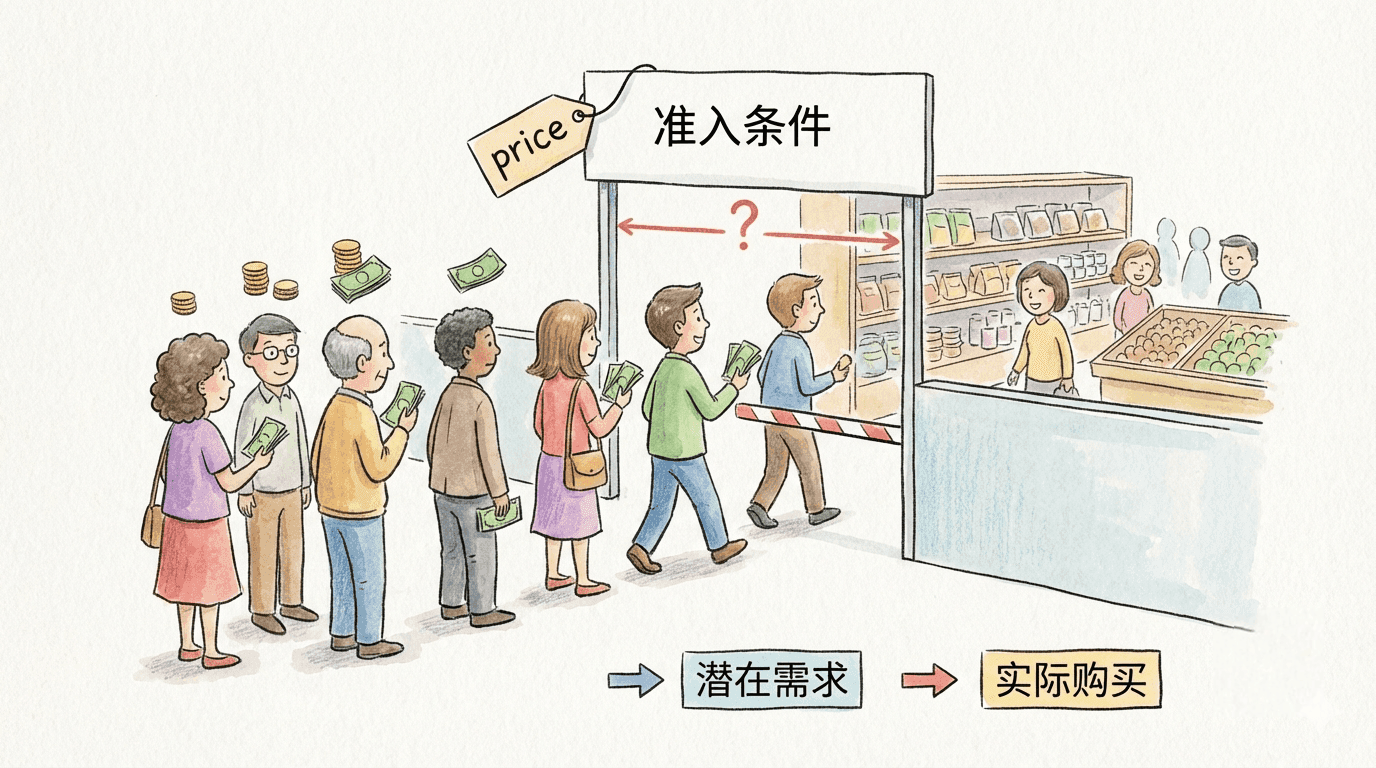
在现实的经济研究和实际数据分析过程中，我们往往会遇到各种特殊的数据现象。例如，有些变量的数据只能被观测到部分区间，其余区间的数据无法获得；有些数据集的观测值在统计前就已经被人为地设置了上限或下限，比如贷款审批时只记录了高于一定额度的申请；还有些情况下，数据由于调查设计或受制于某些条件限制，出现了系统性的缺失，例如只有达到某个标准的人才会被纳入样本。这些情形共同的特点是：观察到的数据并不代表整个总体，往往只揭示了“冰山一角”。

这种情况下，如果我们继续采用传统的回归分析方法，比如普通最小二乘法（OLS），结果很可能会出现偏误，推断也难以反映真实的经济关系。为了解决这个类问题，计量经济学家发展出了一系列专门应对有限或受限因变量的数据建模技术。

受限因变量模型（limited dependent variable models）正是针对上述问题设计的强有力工具。这一类方法主要包含三种基本类型：截断（truncation）、删失（censoring）以及样本选择（sample selection）。其中，截断指的是只有某个范围内的观测值能够进入分析样本，其余被完全忽略；删失是指虽然所有样本都被记录，但某些观测的取值被部分遮蔽或只能看到在某个阈值以上或以下的情况；而样本选择问题通常是由于“能不能进样本”本身就跟我们研究的因变量存在相关关系，从而导致选择性偏差。这些模型在劳动经济学、健康经济学、金融等多个应用领域都有极其广泛的实际意义。

三种数据限制的基本概念

截断问题的现实表现：假如我们要研究全国居民的收入分布，但数据来源只包含年收入超过10万元的高收入群体。这种情况下，我们看不到低收入群体的任何信息，就像是整个收入分布被“截断”了一部分。如果我们直接用这些数据来推断全国的收入水平，结果必然会严重高估。

删失问题的典型场景：考虑一个关于失业持续时间的研究。我们从2020年开始跟踪一批失业者，到2022年研究结束时，仍有部分人没有找到工作。对于这些人，我们只知道他们的失业时间“至少”是两年，但不知道确切的失业结束时间。这种情况就是删失，数据被人为地“截止”在某个时点。

样本选择的微妙之处：例如，我们想研究教育对工资的影响，但只能观察到有工作的人的工资数据。问题在于，是否参与工作本身就可能与教育水平相关，那些高学历但选择不工作的人（比如全职妈妈）的信息就丢失了。这种系统性的数据缺失会导致我们对教育回报的估计出现偏差。

这三种数据限制问题的共同特点是：它们都会导致观察到的样本不再是总体的随机抽样，从而使传统的统计推断方法产生系统性偏差。

---

截断分布的理论基础

截断是受限因变量模型中最基础、也是最常见的情形之一。当我们的观测样本只来自总体的某一个区间时，而希望对整个总体的性质进行外推或推断时，就出现了“截断”问题。这种现象在现实经济数据中极为常见，例如贷款、收入、教育年限等数据收集过程中，由于设计或制度性限制导致低于或高于某阈值的样本被过滤或不可见。

截断分布的数学定义

截断分布，也称为截断条件概率分布，本质上是原始分布在特定区间上的条件分布。假设有一个连续型随机变量 $x$，概率密度函数为 $f(x)$，但我们只能观测到 $x > a$ 的部分，此时的截断分布概率密度可表示为：

$$f(x \mid x > a) = \frac{f(x)}{P(x>a)}, \quad x>a$$

这个公式的经济学直觉是：将原始概率密度在区间 $x > a$ 上重新标准化（即分母为该区间内的概率），保证新的密度函数在该区间内的积分为 $1$。截断的本质影响在于“扭曲”了样本分布，不加处理会直接影响后续的统计推断。

这个图表展示了一个正态分布样本（如中国某城市居民收入）的“低端截断”效应：在年收入低于10万元的数据不可见，仅观察高于此阈值的样本。可以看到，原始分布的右侧被重新做了标准化，截断后分布的形状与均值均发生变化。

截断正态分布的重要数学性质

在实际经济分析中，常用的是截断正态分布。例如 $x \sim N(\mu, \sigma^2)$ 时，若只观测 $x > a$，则其截断后的均值与方差分别为：

截断均值的计算公式

$$E[x \mid x > a] = \mu + \sigma \lambda(\alpha)$$

其中

$$\alpha = \frac{a - \mu}{\sigma}, \qquad \lambda(\alpha) = \frac{\varphi(\alpha)}{1 - \Phi(\alpha)}$$

这里 $\varphi(\cdot)$ 表示标准正态密度函数，$\Phi(\cdot)$ 为标准正态累积分布函数，$\lambda(\alpha)$ 称为逆米尔斯比（inverse Mills ratio）。

截断方差的变化

$$\mathrm{Var}[x \mid x > a] = \sigma^2 \left[1 - \delta(\alpha)\right]$$

其中

$$\delta(\alpha) = \lambda(\alpha)[\lambda(\alpha) - \alpha], \qquad 0 < \delta(\alpha) < 1$$

这些公式提示我们两个核心结论：第一，截断分布的均值会系统性偏移；第二，截断后样本变异程度（方差）总是小于截断前的方差，因为“极端值”被去除了。

高收入人群统计的实际应用

以中国城镇居民收入为例，假设我们对部分经济发达城市的高收入群体进行调研，只掌握了年收入超过10万元家庭的数据。根据某市统计局2022年的数据，假设该市高收入群体（年收入 $>10$ 万元）中，平均收入为18万元，这部分家庭占总城镇家庭的5%。

实际问题：能否利用高收入群体的样本来反推整体收入分布？ 我们设定：

1. $P(\text{收入} \geq 10\ \text{万元}) = 0.05$
2. $E[\text{收入} \mid \text{收入} > 10\ \text{万元}] = 18\ \text{万元}$

假定整个居民的对数收入 $\ln y$ 服从正态分布 $\ln y \sim N(\mu, \sigma^2)$，我们可利用逆米尔斯比公式和边界条件解出分布参数，并进一步预测全体城镇居民的平均收入。

结果显示，即使只掌握了高收入样本，运用截断分布统计原理依然可以对总体情况做出较精确的逆推。这正体现了截断理论在数据受限时的强大价值。

截断分布的两大普遍性结论

1. 均值偏移的规律

若下端截断（只观测 $x > a$），截断样本均值必然大于原分布均值；反之，上端截断（只观测 $x < b$）则截断样本均值小于整体均值。这一规律和直观感受一致：“删去”最小值后，剩下样本平均值自然被抬高。

2. 方差必然缩减

无论截断方式如何，截断分布的方差总是小于或等于原始分布方差。原因在于极端值（离群点）被剔除后，样本数据的波动性降低，分布变得更“集中”。

这两条结论直接提醒我们：截断数据下，直接用样本统计量代表总体参数，会产生系统性偏误。 必须采用如逆米尔斯比修正等方法，针对截断特性做参数的恰当调整，否则分析结果可能被大幅低估或高估。

---

截断回归模型

当我们将截断的概念引入回归分析时，就得到了截断回归模型。这类模型在实际应用中非常重要，因为许多经济数据天然存在截断特征。

模型的基本设定

截断回归模型的基本形式为：

$$y_i = x_i'\beta + \varepsilon_i$$

其中，$\varepsilon_i \mid x_i \sim N[0, \sigma^2]$，但我们只观察到满足$y_i > a$的观测值。

因此，其条件期望为：

$$E[\,y_i \mid y_i > a,\, x_i] = x_i'\beta + \sigma \lambda(\alpha_i)$$

其中 $\alpha_i = (a - x_i'\beta)/\sigma$，$\lambda(\alpha_i)$ 为逆米尔斯比。

边际效应的复杂性

在截断回归模型中，解释变量的边际效应已不再等于回归系数。实际的边际效应为：

$$\frac{\partial E[\,y_i \mid y_i > a,\, x_i]}{\partial x_i} = \beta (1 - \delta_i)$$

其中 $\delta_i = \delta(\alpha_i)$，且 $0 < \delta_i < 1$。这意味着截断会系统性地“衰减”所有解释变量的效应。

普通最小二乘法的问题

如果直接对截断数据使用OLS估计，会遇到严重问题。截断回归模型可写为：

$$y_i = x_i'\beta + \sigma \lambda_i + u_i$$

其中 $u_i$ 为均值为零但异方差的误差项，$\lambda_i$ 项实际上是一个“遗漏变量”，若不考虑，所有系数估计都会偏误。

偏误的方向和程度

理论分析表明，如果$E[x_i \mid y_i]$在完整总体中是$y_i$的线性函数，则OLS估计量会收敛到真实参数的某个比例：$$。实际应用中通常发现，OLS估计结果较最大似然估计更趋近于0（向零偏倚）。

这种偏误的程度取决于截断的严重程度和解释变量的分布特征。截断越严重，偏误通常也越大。

随机前沿模型的重要应用

截断分布理论在随机前沿模型（Stochastic Frontier Model）中有重要应用。该模型最早由Aigner、Lovell和Schmidt于1977年提出，用于分析生产效率。

模型的经济学动机

传统的生产函数认为企业总能达到理论最优生产水平，但实际中企业产出通常低于最优。随机前沿模型引入两个误差项加以描述：

$$\ln y_i = \beta_1 + \sum_k \beta_k \ln x_{ik} + v_i - u_i$$

其中：

• $v_i \sim N(0, \sigma_v^2)$：表示随机冲击与测量误差
• $u_i \geq 0$：表示技术无效率，通常假定服从半正态或指数分布

模型的统计特征

复合误差项 $\varepsilon_i = v_i - u_i$ 服从非对称分布，其概率密度函数为：

$$f(\varepsilon_i) = \frac{2}{\sigma} \varphi\left(\frac{\varepsilon_i}{\sigma}\right) \Phi\left(-\frac{\varepsilon_i \lambda}{\sigma}\right)$$

其中 $\sigma^2 = \sigma_v^2 + \sigma_u^2$，$$。

该模型的分析重点不在回归参数 $\beta$，而在于每家企业的无效率项 $u_i$。通过估计 $u_i$，即可比较不同企业的相对效率。

制造业企业效率分析

下面通过实际案例来理解随机前沿模型。在我国，人们常用该模型对制造业企业的生产效率进行分析。例如，使用国家统计局采集的“中国工业企业数据库”数据，对成千上万家制造业企业的多年度面板数据进行研究。

模型设定

典型的成本（或产出）前沿函数形式为：

$$\ln Y_i = \alpha + \sum_k \beta_k \ln K_{ik} + \sum_m \gamma_m \ln L_{im} + v_i - u_i$$

其中 $Y_i$ 表示第 $i$ 家企业的产出（如工业增加值），$K_{ik}$ 表示资本投入，$L_{im}$ 表示劳动投入， 是统计噪声， 表示技术无效率。

环境变量的处理

中国制造业企业的生产效率也受到诸多外部环境因素影响，这些变量往往不是企业自身直接能够控制的：

不同模型规范的比较

可以看到，不同分布假设会导致效率估计的数值存在差异，这提示在实际应用中需审慎选择假设条件。

效率排名的实际用途

估计每家企业的无效率后，可以据此对企业进行效率排序，这在中国具有多方面的应用价值：

1. 政策制定：帮助政府部门识别低效企业，出台效率提升与技术改造相关扶持措施。
2. 经验总结与推广：总结高效企业的经验，为其它企业提供管理和技术改进的参考。
3. 优化资源配置：在信贷、土地、能源等资源分配上优先照顾效率提升空间大的企业。

目前，类似的效率分析已广泛应用于我国制造业、银行业、交通运输、医疗卫生等领域。

---

删失数据与Tobit模型

删失（censoring）与截断（truncation）是计量经济学中的两个不同概念。删失通常发生在数据收集过程中：我们知道观测值的存在，但只能获得其部分信息。相比之下，截断意味着某些观测完全不可见。

删失的基本概念

现实生活中经常遇到删失，“角点解”（corner solution）是一种经典情形。例如在中国居民消费支出的研究里，许多个体对某些商品的消费量为零。这里的零是受约束后的实际选择，而非数据缺失。删失也普遍存在于医疗、保险理赔（理赔金额有上限/下限）等中国实际场景。

删失与截断的主要区别

删失正态分布的性质

假设潜在变量 $y^* \sim N(\mu, \sigma^2)$，但真实可观测变量 $y$ 定义为：

$$y = \begin{cases} 0 & \text{若}\ y^* \leq 0 \\ y^* & \text{若}\ y^* > 0 \end{cases}$$

于是，删失分布为“离散+连续”混合分布：

• $P(y = 0) = \Phi(-\mu/\sigma)$
• $f(y \mid y > 0) = \dfrac{\varphi\left( \frac{y-\mu}{\sigma} \right)}{\sigma [1-\Phi(-\mu/\sigma)]}$

删失分布矩的推导

删失变量的期望：

$$E[y] = (1 - \Phi(-\mu/\sigma))(\mu + \sigma\lambda)$$

其中 $\lambda = \dfrac{\varphi(\mu/\sigma)}{\Phi(\mu/\sigma)}$ 是逆米尔斯比。

方差为：

$$Var[y] = \sigma^2 (1 - \Phi(-\mu/\sigma)) \left[ (1 - \delta) + (\alpha - \lambda)^2 \right]$$

其中 $\alpha = -\mu/\sigma$，$\delta = \lambda^2 - \lambda\alpha$。

住房市场门票需求的实例分析

假设北京工人体育场有 63,000 个座位，在某赛季中，约 20% 的场次售罄，平均上座 50,000 人。我们想估计真实的门票需求分布——售罄导致的“被删失”数据极为典型。

从上方删失的情况

这种情况属于上方删失，因为实际需求可能超过 63,000，但观测到的数据不会超出座位上线。

删失模型下按照理论公式：

$$E[\text{销售量}] = 63,000 \cdot P(\text{需求} \geq 63,000) + E[\text{需求} \mid \text{需求} < 63,000] \cdot P(\text{需求} < 63,000)$$

已知数据：

• $P(\text{需求} \geq 63{,}000) = 0.20$
• $E[\text{销售量}] = 50{,}000$

带入估计，发现“真实需求”（考虑超额部分）约为 $\mu = 54,300$，方差 $\sigma = 9,100$。

若误把 $50,000$ 当做未售罄场次的均值，则会低估方差和均值，显著影响政策结论。这进一步体现了删失数据识别和正确建模的重要性。

图表反映：删失分布在删失点具备概率质量，而截断分布的概率密度仅剩正区间，并且需重新标准化。中国实际政策分析（如医疗报销、购房限价）中也必须正确认识删失与截断之分。

Tobit模型的经济学应用扩展

Tobit模型（James Tobin, 1958）尤其适合大量零值数据的计量建模。中国实际应用如居民金融资产持有（很多家庭持有为零）、城乡居民购车、农村信贷需求等。

Tobit模型基本形式

$$y_i^* = \mathbf{x}_i'\beta + \epsilon_i \\ y_i = \begin{cases} 0 & \text{若 } y_i^* \leq 0 \\ y_i^* & \text{若 } y_i^* > 0 \end{cases} \\ \epsilon_i \sim N(0, \sigma^2)$$

三类条件期望

• 潜在变量的期望：$E[y_i^* | \mathbf{x}_i] = \mathbf{x}_i'\beta$

其中 $\lambda_i = \frac{ \varphi\left(\frac{\mathbf{x}_i'\beta}{\sigma}\right) }{ \Phi\left(\frac{\mathbf{x}_i'\beta}{\sigma}\right)}$。

边际效应分解（McDonald & Moffitt）

解释变量 $x$ 的影响被分解为：

$$\frac{\partial E[y_i | \mathbf{x}_i]}{\partial x} = P(y_i > 0) \cdot \frac{\partial E[y_i | y_i > 0, \mathbf{x}_i]}{\partial x} + E[y_i | y_i > 0, \mathbf{x}_i] \cdot \frac{\partial P(y_i > 0)}{\partial x}$$

其中第一项为“强度效应”，第二项为“参与概率效应”。

边际效应分解的图形直观（以中国城乡居民购车小时数为例）

图中展示了教育年数对全社会工作小时的边际效应：既通过提升参与概率，也直接提升了工作强度。

中国女性劳动供给Tobit模型案例

近年来中国城乡女性劳动参与下降和“零工经济”盛行，Tobit模型被广泛用于研究妇女劳动供给。

模型变量设定

估计结果举例（实际为模拟中国数据）

研究发现离婚概率的正效应，印证了“预防性储蓄”动机（即离婚风险促使女性更积极参与劳动力市场），和部分发达国家的结论一致。

OLS估计的偏误：直观与实证

在删失存在时简单使用OLS回归会带来严重的低估偏误，尤其是在住房、金融等中国实际领域。一般规律是：OLS估计的绝对值显著小于最大似然估计（MLE），比例约等于非零观测占比。

为什么会偏误？

使用OLS时，所有零观测直接作为零计入，实际却忽略了背后的“潜在需求/劳动/消费”。这导致：

1. 参数系数向零偏倚：低估 $x$ 的效应
2. 方差被低估：高频零值稀释了残差
3. 实际预测失真：模型无法反映需求的真实结构

在中国宏观和微观数据中，删失比例越高，这种低估越严重——正是Tobit模型不可替代的重要原因。

---

持续时间模型与生存分析

持续时间（生存）分析关注某一事件持续的时间及其决定因素。这类分析最初源自医学统计——如研究患者从治疗到复发或死亡的时间，但其方法已广泛应用于经济学、金融学、社会学等领域。例如分析贷款违约时间、雇员在职持续时间、在线订阅保持时间、电商顾客首次复购等待期、政策试点持续期、企业退出市场时间等。

持续时间数据的特殊性质

持续时间数据与传统横截面数据的本质区别是：我们关心的不仅是事情“是否”发生、更重要的是“何时”以及“为什么在这个时点”发生。与之相关，持续时间分析核心在于在给定已经存续一段时期的条件下，该事件结束的概率（即危险率）的建模与解释。

经济学及相关领域中的典型应用举例

例如：一项关于互联网视频平台会员流失的研究，关注会员自开通日起，经历的实际使用天数，直到取消订阅为止。

生存函数与危险函数

持续时间分析有两个核心函数：生存函数 $S(t)$ 和危险函数 $\lambda(t)$。

生存函数 $S(t)$

生存函数给出事件持续到时间 $t$ 及之后的概率，其公式为：

$$S(t) = P(T \geq t) = 1 - F(t)$$

其中 $T$ 为事件持续时间，$F(t)$ 为 $T$ 的累积分布函数。

危险函数 $\lambda(t)$

危险函数（hazard function，又称风险函数）衡量在事件已持续到 $t$ 的条件下，于接下来极短时间内结束的即时概率，形式为：

$$\lambda(t) = \lim_{\Delta t \to 0} \frac{P(t \leq T < t+\Delta t \mid T \geq t)}{\Delta t} = \frac{f(t)}{S(t)}$$

其中 $f(t)$ 是持续时间 $T$ 的概率密度函数。

函数之间的关系公式

三者的关系可归纳如下：

$$\lambda(t) = -\frac{d \ln S(t)}{dt}$$ $$S(t) = \exp\left(-\int_0^t \lambda(s) ds\right)$$ $$f(t) = \lambda(t) S(t)$$

这些数学关系确保模型刻画事件发生的动态和概率基础。

不同危险函数的经济含义与形态

危险函数的形态蕴含不同经济行为机制：

常数危险率（指数分布）

如果 $\lambda(t) = \lambda$ 为常数，则事件发生的概率与已经经历的时间无关，即“无记忆效应”（memoryless），例如某些竞技游戏中的突发死亡风险与生存时长无关。

递增危险率

$\lambda(t)$ 随 $t$ 增大，例如新创企业存活时间越长，倒闭风险越高，原因可能是“幸存者”逐渐面对市场淘汰。

递减危险率

$\lambda(t)$ 随 $t$ 减小。如消费者购车等待时间越久，放弃购车意愿（事件 = 放弃购车）概率其实逐步下降。

非单调危险率

$λ(t)$ 存在上升与下降阶段。现实中常有“蜜月效应”——如新产品上市初期流失高、之后留存趋于稳定，或劳动力市场的初期高转职率，随后趋稳。

危险函数形态可视化对比

如上图，不同生存模型代表不同经济假设。指数模型暗含危险率恒定；威布尔可捕捉单调变化；对数正态和对数逻辑允许峰值或复杂变化，便于反映时间依赖性和混合机制。

参数化生存模型

现实研究常使用以下参数化模型：

威布尔模型（Weibull）

危险函数：

$$\lambda(t) = \lambda p (\lambda t)^{p-1}$$

生存函数：

$$S(t) = \exp\left(-(\lambda t)^p\right)$$

若 $p>1$ 危险率递增；$p<1$ 递减；$p=1$ 退化为指数分布。可描述“加速故障”或“磨损期”等场景，例如设备失效、生物寿命等。

对数正态模型（Log-normal）

假设 $\ln(t) \sim N(\mu, \sigma^2)$，危险函数先上升后下降，适合峰值概率存在的持续时间分布，例如企业新产品的流行周期。

对数逻辑模型（Log-logistic）

危险函数形式为：

$$\lambda(t) = \lambda p (\lambda t)^{p-1} / [1 + (\lambda t)^p]$$

支持危险率初升后降，比对数正态模型更加灵活。适用于建模如投资项目持有时间、IT行业员工在职周期等。

互联网用户流失持续时间分析

以某在线教育平台用户首次流失时间为例。研究样本为一年内首次下单的用户，关注其“活跃天数”（从注册到最近一次登录之间的天数）。

样本统计

不同模型估计对比

经济变量举例与解释

进一步考虑了“日均学习时长”对流失风险的影响，得到威布尔回归结果：

$$\ln \lambda_i = 2.233 - 4.501 \times (\text{日均学习时长})$$

结论：

1. 学习时长提升显著降低用户流失风险；
2. 每增加1小时，流失中位持续天数增长约2.3天；
3. 反映了平台黏性与客户留存内生动力。

非参数与半参数生存分析方法

除了参数化模型，实际分析还常用如下方法：

Kaplan-Meier 估计量（KM法）

典型非参数估计法，对$S(t)$形态无假定直接估计：

$$\hat{S}(t) = \prod_{k:t_k \leq t} \left( \frac{n_k - h_k}{n_k} \right)$$

$n_k$ 为 $t_k$ 时风险集人数，$h_k$ 为 $t_k$ 观测到的事件数。例如可以用于估算用户续费率曲线、疾病患者存活概率等。

Cox比例风险模型（半参数）

当前流行的半参数建模思路，危险函数可分解为

$$\lambda_i(t) = \lambda_0(t)\exp(x_i'\beta)$$

$\lambda_0(t)$ 为弹性基准危险函数，无需参数形式，$x_i$为协变量。Cox模型可以估计如“营销活动”、“服务满意度”等因素对流失率的相对影响，适用性强。

删失（Censoring）数据的处理

持续时间数据几乎总伴随删失，即在分析期结束时部分样本事件尚未发生（如用户尚未流失、贷款尚未违约）。

删失数据下似然函数构造

对删失数据，似然函数一般为：

$$L = \prod_{i\in\text{未删失}} f(t_i) \times \prod_{j\in\text{删失}} S(t_j)$$

• 未删失观测用概率密度$f(t)$，删失观测用生存概率$S(t)$。

若忽视删失，估计偏误将产生：

1. 平均持续时间被低估（实际比观测更长）
2. 危险率被高估
3. 导致对风险/机会的错误决策

删失正确处理是所有生存分析的核心步骤，对于医疗临床、生物统计、平台产品留存等研究都至关重要。

---

样本选择问题与Heckman模型

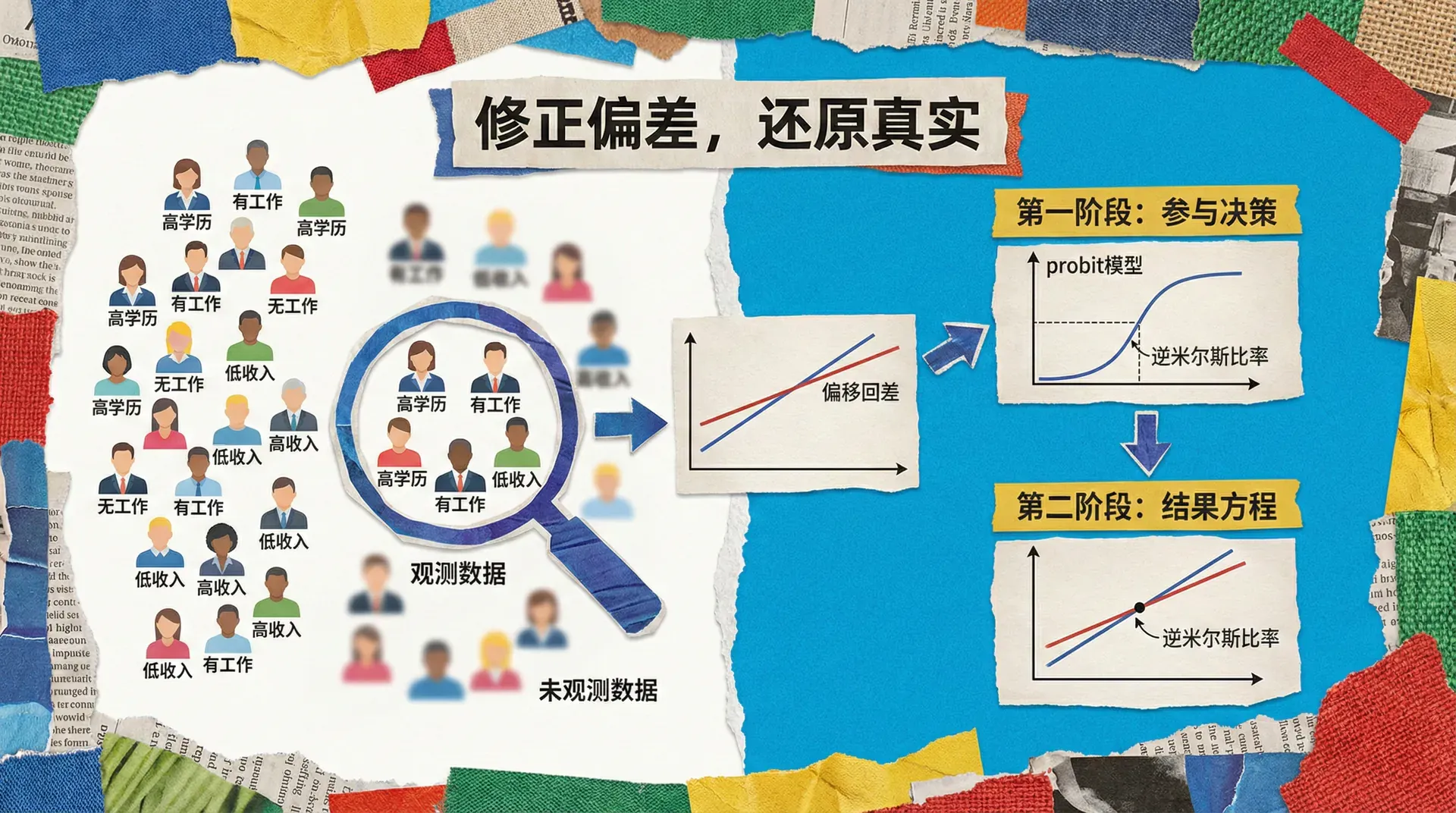
样本选择问题（Sample Selection Problem）是受限因变量模型中一个尤其复杂且基础性的话题。当我们手头的数据并非来源于整体随机抽样，而是经过某种机制“筛选”后形成的观测样本时，就会出现样本选择偏差。这种偏差已经广泛存在于社会科学、生命科学、商业数据分析等领域。

样本选择的基本含义与偏差

样本选择的核心在于“选择性偏差（Selection Bias）”：我们能够观察到的数据，往往系统性地不同于整个目标总体，这种不同不是随机噪声，而是与本就关心的结果变量密切相关。其后果是，使得基于样本的回归、均值推断等分析不再具有泛化能力。

选择性偏差例子：

1. 医疗治疗有效性分析：只有主动就医或有条件支付治疗费用的患者会被录入数据，他们往往健康状况更糟或社会经济地位更高，导致估计治疗效果与整体病患存在偏差。

2. 互联网金融信贷违约分析：只能观察已获批贷款用户的违约，实际上有很多申请人未获批，如果仅在放款样本上估计违约模型，得出的风险水平会比真实环境偏低。

3. 运动员表现研究：只统计参加决赛运动员的数据，而忽略大量未晋级者——这样可能高估训练计划对成绩的提升作用。

双变量正态分布与截断机制

样本选择问题的理论基础是“双变量正态分布的条件截断”。假设有两个变量 $y$ 和 $z$，它们联合服从双变量正态分布，协方差为 $\rho$。只有当 $z$ 超过某个阈值 $a$ 时，$y$ 被观测到。此时，截断后的 $y$ 的条件期望为：

$$E[y \mid z > a] = \mu_{y} + \rho \sigma_{y} \lambda(\alpha_z)$$

其中：

$$\alpha_z = \frac{a - \mu_z}{\sigma_z}, \hspace{24pt} \lambda(\alpha_z) = \frac{\varphi(\alpha_z)}{1 - \Phi(\alpha_z)}$$

$\varphi(\cdot)$ 和 $\Phi(\cdot)$ 分别为标准正态概率密度和分布函数，$\lambda(\cdot)$ 被称为“逆米尔斯比”。

选择性偏差的判断与规律

• 若 $\rho > 0$ 且从下方截断，观测到的 $y$ 均值高于总体均值
• 若 $\rho < 0$ 时，观测均值反而低于总体
• 偏差程度取决于相关性 $\rho$ 与截断严重性（即 $a$ 的高低）

选择性偏差直观演示

该图可视化展现：一旦我们只观测 $z > 0$ 的点，而 $y$ 与 $z$ 呈正相关，被选中的 $y$ 明显整体高于未选区，因此“样本均值”天然偏高。

Heckman两步估计法

为数据因选择性受限而导致的偏差校正，James Heckman（1979）提出了著名的“两步法”：

模型设定
选择方程（Selection Equation）：

$$z_i^* = w_i' \gamma + u_i,\qquad z_i = 1 \text{ if } z_i^* > 0$$

结果方程（Outcome Equation）：

$$y_i = x_i' \beta + \varepsilon_i, \qquad \text{仅当 }z_i=1\text{ 时观测到 } y_i$$

假定 $\begin{pmatrix} u_i \\ \varepsilon_i \end{pmatrix}$ 服从均值为零、相关系数为 $\rho$ 的双变量正态分布。

两步法的操作流程

高校毕业生工资分析

为了替换下新的例子，这里以高校毕业生就业及工资收入为案例：

传统工资回归模型只纳入已就业毕业生，未就业或出国深造者被遗漏。然而就业与否与收入能力可能同被影响，例如学习成绩、社会网络等未被直接观测的特质。直接使用就业者样本会高估毕业生平均工资。

主要变量

• 选择方程变量：性别、是否有实习经历、专业类型、毕业院校层次、家庭背景
• 工资方程变量：学历、GPA、工作城市等级、企业性质

估计结果示意

• 两步校正后，发现标准OLS高估了学历与GPA带来的工资提升。

信贷审批与违约的双变量选择性

在互联网金融领域，信贷审批通常先有“能否获批”（选择方程），再有“获批后的违约风险”（结果方程）。

模型结构

选择方程（审批）：

$$d_i^* = z_i'\eta + u_i, \qquad d_i = 1\ \text{if} \ d_i^* > 0$$

结果方程（违约）：

$$y_i = x_i'\beta + \epsilon_i,\qquad 仅当 d_i=1 \text{时有违约观测}$$

实际估计时，我们往往用带有选择修正项的Probit/Logit模型。

实际结果对比：

$^*$, $^{**}$, $^{***}$表示统计显著性。
可以发现，不考虑选择偏差会低估真实违约风险。

双变量Probit在非线性选择模型中的用法

当因变量本身是二元（如是否违约、是否肝炎阳性等），需要采用双变量Probit模型：

$$\begin{align*} \Pr(z_i = 1) &= \Phi(w_i'\gamma) \\\\ \Pr(y_i = 1 | z_i = 1) &= \frac{\Phi_2(x_i'\beta,\, w_i'\gamma,\, \rho)}{\Phi(w_i'\gamma)} \end{align*}$$

其中 $\Phi_2$ 表示二元正态分布的联合累积函数。

医疗保险选择与住院治疗案例

以某省医保数据为例：

显著的负相关表明未参保群体对住院需求结构性不同，证明双变量方法的必要性。

面板数据与样本流失（Attrition Bias）

在纵向（面板）数据研究中，个体随时间退出样本（流失）会导致样本选择偏差。如果流失倾向与结果变量相关，偏差会更严重。

常见处理策略

1. 逆概率加权（IPW）：基于留样概率对样本赋权，常见于医疗随访、用户留存分析等场景。如分析按月活跃的APP用户数据时，活跃概率低的样本赋更大权重。
2. 联合概率模型：同时建模观测和退出方程
3. 工具变量法：寻找只影响流失但不影响主结果的变量作为工具

具体策略应根据数据生成机制（DGP）与目标问题灵活选择。

---

总结

受限因变量模型为处理现实中复杂的数据结构提供了强大的工具集。从简单的截断分布到复杂的样本选择模型，这些方法帮助我们从有限的、有偏的数据中提取可靠的信息。

三种数据限制的本质区别

方法论的演进脉络

受限因变量模型的发展体现了计量经济学从描述性分析向因果推断的转变：

1. 早期阶段：主要关注如何正确估计参数，代表性工作是Tobin的删失回归模型
2. 发展阶段：开始关注选择性偏差问题，Heckman的样本选择模型是里程碑
3. 现代阶段：强调因果识别和政策评估，发展出多种稳健的识别策略

当前面临的挑战

随着大数据和多源信息的普及，受限因变量模型面临新的选择性偏差挑战，包括算法偏差、数据缺失机制复杂化及隐私保护限制。同时，因果推断在政策评估中提出更高要求，如异质性分析、动态效应与一般均衡效应等。

为应对这些挑战，方法论持续创新，包括机器学习与传统模型结合、非参数/半参数方法及贝叶斯推断的应用。应用领域不断拓展至数字经济、环境经济与金融科技等，计算技术也快速演进，如并行计算、云平台和可视化工具，都助力模型大规模精准实现。

受限因变量模型的进步推动经济学由描述走向因果推断，掌握这些方法有助于培养科学思维和批判性分析能力。