垄断理论与市场效率

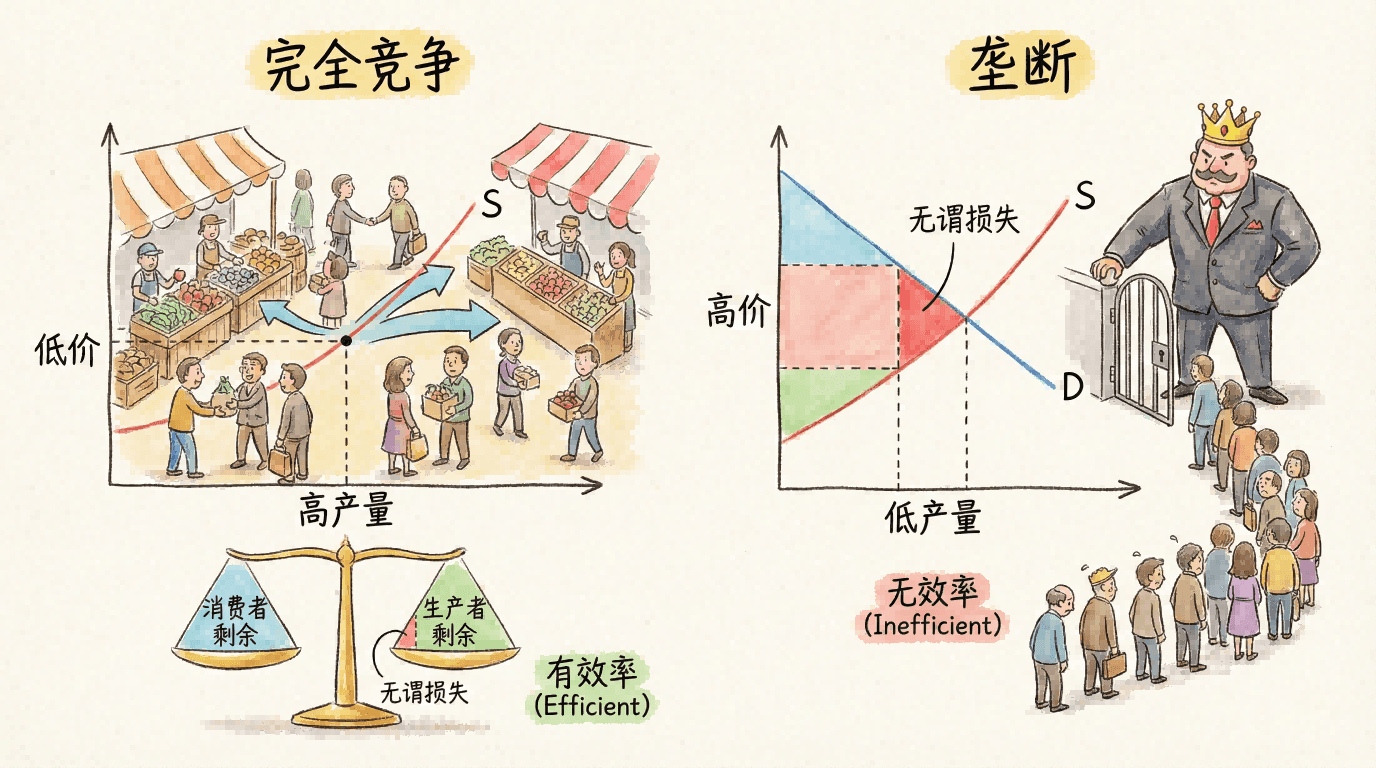
当市场中只有一个企业时，即形成了垄断市场结构。在这种情况下，企业不会像完全竞争市场那样将市场价格视为“给定”，而是会主动关注自己的生产和销售决策对市场价格的直接影响。垄断者能够通过调整产量和价格，在一定范围内控制整个市场的供给和价格水平，从而选择能够最大化企业整体利润的最优价格和产出组合。

垄断不仅仅是经济理论中的一种抽象模型，它在现实经济中有着广泛的表现形式。例如，传统公用事业行业如电力、天然气、自来水等由于规模经济和设备专有性，使得一个企业占据整个市场成为可能。此外，现代科技领域的某些公司（如操作系统、主流搜索引擎、重要社交媒体平台等），依靠技术壁垒、品牌优势、网络效应，往往也能够形成类似垄断的市场支配地位。这些垄断力量对市场价格、产品创新、消费者选择以及社会资源配置产生了持续而深远的影响，使得市场结果经常偏离有效率的竞争状态。

在垄断条件下，企业通常拥有更强的议价能力和更高的利润空间，但这种市场结构也可能带来负面的社会后果。例如，垄断可能导致价格高于边际成本，产量低于社会最优水平，从而引发“死重损失”，损害消费者福利。同时，垄断企业的创新动力和服务质量也可能因缺乏竞争压力而下降。另一方面，垄断有时也能通过规模经济或技术研发带来社会效益，因此实际政策需要在促进效率与保障公平之间权衡。

理解垄断的经济学原理，对制定反垄断政策、进行市场监管以及企业的战略决策都具有基础性和现实指导意义。只有深入把握垄断行为的形成机制、市场影响及其外部性，才能更好地推动市场健康有序发展，提升社会整体福利。

---

垄断的利润最大化

垄断者的优化问题

在垄断市场结构中，企业面临着市场的全部需求，能够自由选择产量和价格。我们用 $p(y)$ 表示市场反需求曲线，用 $c(y)$ 表示总成本函数。垄断企业的收入函数为 $r(y) = p(y) \cdot y$，其目标是选择一个产量 $y$ 使得利润最大。用公式表达，可以写为：

$$\max_{y} \ \pi(y) = r(y) - c(y) = p(y)\cdot y - c(y)$$

要实现利润最大化，垄断者需要令利润关于产量的一阶导数为零，即一阶最优条件：

$$\frac{d\pi(y)}{dy} = \frac{dr(y)}{dy} - \frac{dc(y)}{dy} = 0$$

这实际上等价于：

$$MR = MC$$

其中，$MR$ 表示边际收入（Marginal Revenue），$MC$ 表示边际成本（Marginal Cost）。这意味着在最优产量水平上，垄断者希望每再增加一单位产出所带来的额外收益刚好等于其成本，超过这个点就不再增加利润。

边际收入的经济含义

垄断者与完全竞争企业的最大不同在于：提高产量不仅会带来新增产品销售的收入，还会导致所有产品的市场价格下降，因此边际收入的计算更复杂。当垄断者将产量增加 $\Delta y$ 时，收入变化可以拆解为两个部分：

1. 正效应：新增 $\Delta y$ 单位产出可按当前价格 $p$ 售出，带来 $p \Delta y$ 的收入。
2. 负效应：供给增加使得市场价格从 $p$ 降为 $p + \Delta p$，其结果是原有 $y$ 单位的售价下降，总计损失 。

这两者合计，垄断者的总收入变化为：

$$\Delta r = p \Delta y + y \Delta p$$

由此得到边际收入的表达式：

$$MR = \frac{\Delta r}{\Delta y} = p + \frac{\Delta p}{\Delta y} y$$

每增加一单位产出，垄断者不仅要计算新增售出部分的价格，还要考虑对全部已售数量因价格下调带来的损失。这种对“全量价格变动”的关注，是垄断与完全竞争的根本区别。

边际收入与需求弹性的关系

进一步来看，边际收入还可以和需求弹性联系起来表达。设需求价格弹性为 $\varepsilon(y)$，我们可以将边际收入写为：

$$MR(y) = p(y) \left[1 + \frac{1}{\varepsilon(y)}\right]$$

由于需求弹性 $\varepsilon$ 对绝大多数正常商品来说为负数，上式通常也被写作：

$$MR(y) = p(y) \left[1 - \frac{1}{|\varepsilon(y)|}\right]$$

由此得到垄断的最优化条件：

$$p(y)\left[1 - \frac{1}{|\varepsilon(y)|}\right] = MC(y)$$

这种公式表达了需求弹性越大（绝对值越大），$MR$ 越接近于 $p$，越趋近于完全竞争的情形。

在完全竞争情况下，需求弹性趋于负无穷，即 $|\varepsilon|\to\infty$，所以 $1/|\varepsilon|\to 0$，此时 $MR\approx p$，最优条件退化为 $p = MC$，这与我们对完全竞争均衡的结论一致。

垄断者永远不会选择在需求缺乏弹性的区域（$|\varepsilon| < 1$）经营。因为这时 $MR < 0$，总利润无法实现最大化。

需求弹性与垄断决策

为什么垄断者绝不会在非弹性区间经营？数学上，可以这样说明：当 $|\varepsilon| < 1$ 时，有 $\frac{1}{|\varepsilon|} > 1$，带入前面公式：

$$MR = p \left[1 - \frac{1}{|\varepsilon|}\right] < 0$$

此时每多生产一单位产出反而会降低总收入，而减少产量则能“收窄供给—拉高价格”，从而增加总收入和利润。因此利润最大化的产量必然只能出现在 $|\varepsilon| \ge 1$ 的弹性区间内。

所以，垄断企业理性经营的一条铁律，就是只在需求曲线弹性区间选择产量和定价。

---

线性需求曲线下的垄断

线性需求的标准分析

假设垄断者面临一条线性需求曲线，其表达式为：$p(y) = a - by$ 其中 $a$ 为需求曲线的纵轴截距，$b$ 为斜率（$b>0$）。对应的总收入函数为：

$$r(y) = p(y)\cdot y = ay - by^2$$

这是一个关于产量的二次函数，体现了随着产量增加，收入先增后减的特征。边际收入（Marginal Revenue, $MR$）作为总收入关于产量的导数，则有：

$$MR(y) = \frac{dr(y)}{dy} = a - 2by$$

可以看出，边际收入本身也是一条直线，其斜率为需求曲线的两倍且更陡峭，截距不变为$a$。

在图形上，需求曲线与边际收入曲线有以下重要联系：它们具有相同的纵截距$a$，但$MR$的斜率为$-2b$，即边际收入随产量增加减少得更快。需求曲线的水平截距是 $y = a/b$，而边际收入曲线的水平截距则为 $y = a/(2b)$，正好是一半。

对于图像绘制，首先在纵轴上取$a$为截距，然后分别在数量轴上取需求曲线的截距 $y=a/b$ 和边际收入曲线的截距 $y=a/(2b)$，连线即可分别得到需求曲线和$MR$曲线。

进一步地，垄断均衡的产量与价格是这样确定的：首先，找到$MR$和边际成本曲线$MC$的交点，设该点对应的产量为 $y^*$，此时有

$$MR(y^*) = MC(y^*)$$

再将最优产量 $y^*$ 代入需求函数，得到最优价格 $p^* = a - b y^*$。

当已知平均成本$AC(y^*)$时，此时的垄断利润为：

$$\pi^* = (p^* - AC(y^*))\cdot y^*$$

垄断利润最大化的本质，在于“产量$y^*$选择于$MR=MC$，对应价格由需求曲线决定”。

图形分析中的关键曲线与要素

在垄断均衡的图像分析中，通常包含如下几条核心曲线与对应作用：

• 需求曲线，表达市场上每一产量水平下，消费者愿意支付的最高价格，斜率为 $-b$。
• 边际收入曲线，表达额外生产一单位产出所带来的边际收益，斜率为 $-2b$，用于确定最优产量。
• 边际成本曲线MC，即每多生产一单位需付出的额外成本，是厂商的技术和成本约束。
• 平均成本曲线AC，用于计算利润和衡量市场进入壁垒。

均衡分析通常遵循这样的逻辑：

1. 产量选择：找出 $MR = MC$ 的交点，求得最优产量 $y^*$。
2. 定价逻辑：以 $y^*$ 带入需求曲线，确定最优价格 $p^*$。

利润最大化的直观几何解释：垄断者生产到$MR=MC$为止，把产量卖给市场，最终售价由那一刻的需求曲线决定。

---

加价定价策略

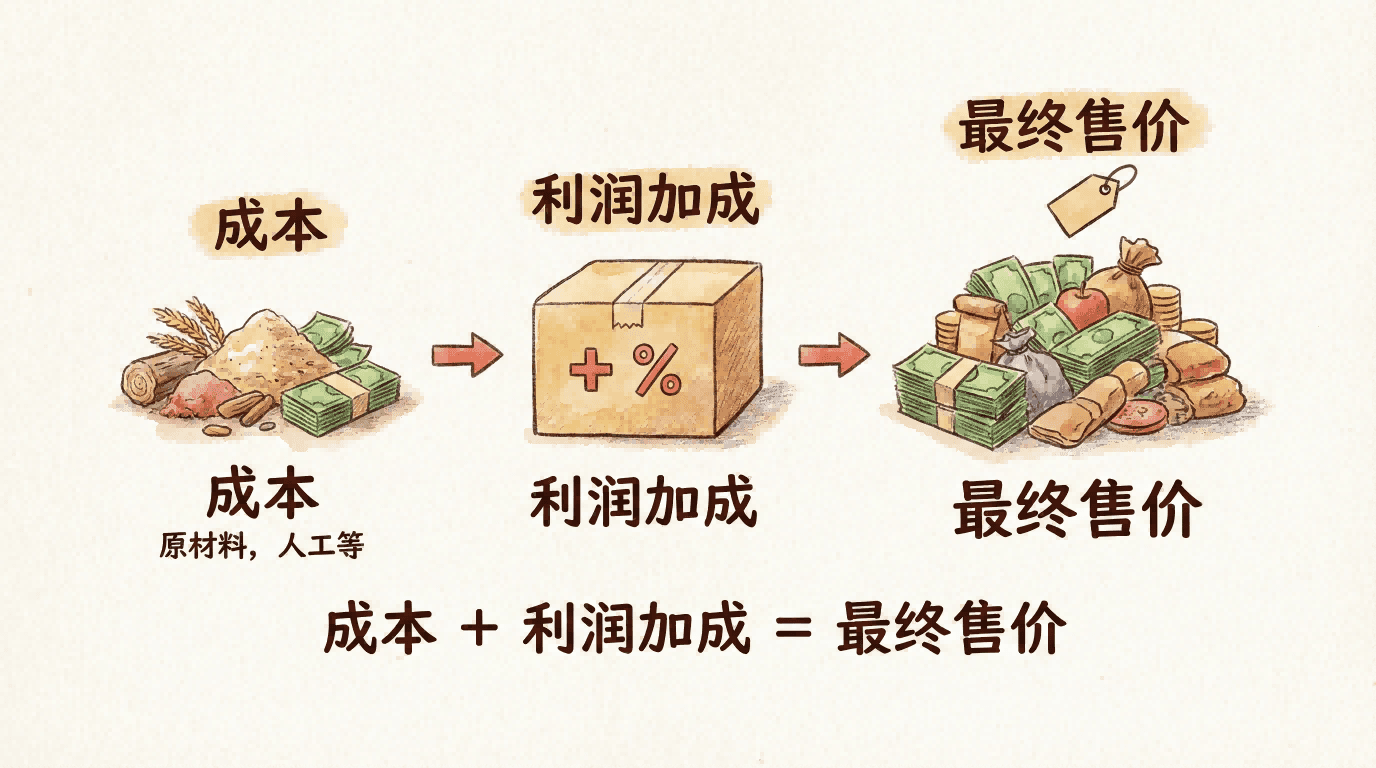
用需求弹性解释垄断的加价行为

在更一般的情形下，垄断者的最优定价不仅取决于成本，也强烈依赖于需求弹性。数学上，最优定价可以用如下“加价公式”表达：

$$p^* = \frac{MC(y^*)}{1 - \dfrac{1}{|\varepsilon(y^*)|}}$$

其中 $MC(y^*)$ 是最优产量下的边际成本，$|\varepsilon(y^*)|$ 为这一点的需求价格弹性绝对值。右侧分母中的 $1 - 1/|\varepsilon|$ 因为，总是小于1，从而，即出现加价现象。

定义“加价倍数”（markup）为：

$$\text{markup} = \frac{p^*}{MC} = \frac{1}{1 - \dfrac{1}{|\varepsilon|}}$$

由此可见，需求越不富有弹性（$|\varepsilon|$ 越小），分母越小，加价倍数越大，垄断者可以收取更高的价格。

实际经济含义如下：当需求越欠缺弹性时，消费者对涨价“不敏感”，企业加价空间很大；反过来，若需求极富弹性，则价格提升会使销量下降严重，企业只能采取较低加价，甚至最终逼近完全竞争时的水平（$|\varepsilon|\to\infty$，$\text{markup}\to1$）。

| 需求弹性($|\varepsilon|$) | 加价水平 | 经济含义 | |-----------------|-----------|---------| | 欠缺弹性（小于但大于1） | 加价很高 | 消费者对价格变动不敏感，企业有较强议价能力 | | 弹性较大 | 加价较低 | 消费者对价格敏感，加价空间有限 | | 极大弹性($|\varepsilon|\to\infty$) | 加价趋于1 | 接近完全竞争结果 |

企业在制定价格时，需参考自己产品在不同市场和情境下的需求弹性——生活必需品因缺乏弹性往往加价高，奢侈品由于弹性较大，加价水平反而有限。

恒定弹性需求下的定价特征

对于一些市场，需求弹性在全产量区间都比较稳定，即“恒定弹性”需求。这种情况下，垄断者的定价公式显得尤为简洁：

$$p^* = \frac{MC}{1 - \dfrac{1}{|\varepsilon|}}$$

因为$|\varepsilon|$ 是常数，最优价格总是边际成本的一个固定倍数。这有如下管理优势：

• 定价决策更为直接、简单。
• 有利于在成本波动时及时调整产品价格。
• 长期可获得相对稳定的利润率。

图像表现为：如果把$MC$曲线放大$1/(1-1/|\varepsilon|)$倍，取其与需求曲线的交点，即为最优产量与价格。

相关行业案例包括：公用事业、专利药品、部分高端奢侈品等，这些行业因市场需求弹性相对恒定，企业加价能力较强、定价规则更硬。

---

税收对垄断者的影响

数量税影响的分析

现在考虑政府向垄断者征收每单位产品$t$元的数量税。假设需求曲线仍为线性 $p = a - by$，边际成本为常数 $MC = c$。

此时，税后边际成本上升为 $MC_{税后} = c + t$，利润最大化的一阶条件：

$$a - 2by = c + t$$

解得最优产量：

$$y^*_{税后} = \frac{a - c - t}{2b}$$

税前的最优产量为 $y^*_{税前} = \frac{a - c}{2b}$，税收每增加$1$，产量减少$$。

最优价格也相应提升：

$$p^*_{税后} = a - b y^*_{税后} = a - b\cdot\frac{a-c-t}{2b} = \frac{a + c + t}{2}$$

可见，每单位税额$t$，最终价格仅上涨$t/2$，即价格上升了“税收的一半”。如果绘制相关图形，发现税前后的$MC$曲线向上平移$t$，新均衡点与需求交点右移。

在线性需求和恒定边际成本下，每单位税收只被价格转嫁了一半，剩余一半由企业自行承担。

不同需求结构下的税收效应

如果垄断企业所面临的是“恒定弹性”需求，则最优定价是：

$$p^* = \frac{c+t}{1 - \dfrac{1}{|\varepsilon|}}$$

这时，价格对税收的敏感度大于1，即

$$\frac{\Delta p^*}{\Delta t} = \frac{1}{1 - \dfrac{1}{|\varepsilon|}} > 1$$

说明每加1元税，最终价格上涨幅度甚至超过1元，由消费者转嫁更多负担。弹性越低（$|\varepsilon|$越小），转嫁比例越大。

对于利润税（例如对总利润按比例收取而非按产量计征），最优产量并不会受到影响。数学表达为企业最大化 $(1-\tau)[p(y)y - c(y)]$，其中$\tau$为利润税税率，但决定产量的一阶导数不变。因此，纯利润税对垄断者的产出选择没有扭曲效应。

---

垄断的无效率性

帕累托效率的比较分析

在完全竞争的市场结构中，企业的生产决策使得市场价格始终等于边际成本，即 $p_c = MC(y_c)$，因此能够实现帕累托有效的资源配置。然而，在垄断市场中，企业为了利润最大化，会在边际收入等于边际成本时才选择产出。由于垄断企业面临的是向下倾斜的需求曲线，所以会出现 $p_m > MC(y_m)$ 的状况，导致垄断产量 低于竞争产量 ，价格也高于竞争水平，即 。

通常，我们可以通过下表进行对比：

垄断的无效率性来源于，在 $y_m$ 到 $y_c$ 之间的所有产出量上，消费者愿意支付的价格 $p(y)$ 都高于该单位商品的边际成本 $MC(y)$，因此存在替代性的交易，这些交易能够让买卖双方获取额外的剩余，从而带来帕累托改进，但由于垄断者的产出限制，这些交易并没有发生。

无效率的经济逻辑详细解析

实现有效的资源配置，需要每一单位的边际支付意愿等于边际生产成本。对于竞争性企业而言，他们只需比较边际收益（即价格）与边际成本，当 $p = MC$ 时达到最优。而对于垄断企业而言，其决策不仅要比较边际收益和边际成本，还必须考虑增加产量会使得所有单位的价格下降，即边际收入 $MR$ 低于价格 $p$。这一点直接导致垄断优化产量低于帕累托有效产量。

垄断者的生产决策不仅取决于边际收入与边际成本的比较，还要计算增加一单位产出对所有已售单位收入的“负面影响”。因此，垄断总是有强烈的动机以低于现有市场价格出售额外单位产出，但前提是如果可以不降低所有单位的销售价格（即存在完全价格歧视）。

垄断者如果能够针对每个消费者以不同价格销售（完全价格歧视），则愿意增加产出并接近竞争性产量。然而实际中，垄断者往往无法实行完全价格歧视，导致所有单位必须以统一价格出售，从而产生产量不足和福利损失。

---

垄断的死重损失

死重损失的测量

明确了垄断带来的无效率后，我们进一步关心，这种无效率性到底“有多大”？死重损失（Deadweight Loss, DWL）就是用来度量因为垄断导致的社会福利净损失的概念。简单来说，死重损失指在垄断产量与竞争产量之间，社会本可获得却因为生产不足而丧失的盈余总量。

在图形分析中：

• 竞争均衡：$P = MC$，产量为 $y_c$
• 垄断均衡：$MR = MC$，产量为 $y_m < y_c$

因此，死重损失为需求曲线 $P(y)$ 与边际成本曲线 $MC(y)$ 之间，在 $y_m$ 到 $y_c$ 区间所围成的面积。

分析死重损失可以从两个方面进行具体分解：

• 消费者剩余的变化：从垄断转向竞争后，原本因价格过高被排除在市场之外的消费者现在可用更低价格购买，获得了面积 $A$，而因产量增加部分又带来面积 $B$ 的新增剩余，总变化为 $A+B$。
• 生产者剩余的变化：由于整体价格下降，部分生产者剩余损失了面积 $A$，但因增加产量又获得了面积 $C$ 的补偿，净变化为 $C-A$。

净社会效应综合起来，面积 $A$ 再分配于消费者与生产者之间，并不改变总福利，而 $B+C$ 才是真正的社会福利净增加。由此：

$$\text{死重损失} = B + C$$

死重损失直观地反映了，社会为实现垄断价格所付出的福利损失：生产者与消费者都因“少生产、价偏高”而失去本可获得的剩余。

死重损失的价值测量

用公式的方式，假设垄断产量为 $y_m$，竞争产量为 $y_c$，那么死重损失可以写作：

$$\text{死重损失} = \int_{y_m}^{y_c} [P(y) - MC(y)] \, dy$$

每扩大一单位产出，从垄断数量到竞争数量，社会能够获得的净价值就是价格与边际成本的差额。累加所有 $y_m$ 到 $y_c$ 的区间，得到的就是因垄断而未实现的总净福利。

---

自然垄断

自然垄断的基本概念

回顾上面分析，帕累托有效产出要求价格等于边际成本，即 $P = MC$。在多数行业，这是实现效率最大化的理想选择。但在自然垄断行业，情况却有很大不同。

自然垄断的本质特征在于固定成本极高、边际成本极低——也就是说，成本结构导致平均成本曲线随着产量增加而长期递减。典型的自然垄断行业如天然气输送、电力、公用电话等，都需要大规模的基础设施投入，而一旦建成，单个用户的边际供给成本几乎可以忽略不计。

具体而言，对于自然垄断者来说，其平均成本随产量扩大会不断下降，在整个市场需求范围内，单一企业服务最为高效，多家企业反而会导致资源的浪费。

经济技术逻辑：一旦基础设施建成，所有新增客户的服务边际成本都非常低。

如果单个企业在实现有效产出 $P=MC$ 时依然亏损，即平均成本 $AC > P$，那么垄断就具备“自然性”：行业不可避免地只容许一家企业存在，这就是自然垄断的定义。

自然垄断的监管困境

面对自然垄断，政府监管在效率与公平之间陷入两难选择。常见监管定价方案主要有三种：

1. 边际成本定价：设置 $P = MC$，能够实现有效产出最大化，但由于 $AC > MC$，企业普遍面临亏损，不可持续。需政府补贴才能长远运行。
2. 垄断定价：允许企业选择 $MR = MC$ 时的价格与产量，企业获得利润，产量不足，效率损失显著，但无需补贴。
3. 平均成本定价：监管当局让企业 $P = AC$，使企业收支平衡，虽然产量仍低于帕累托最优，但较垄断产量更接近效率。

政策选择方面，各国监管实践包括政府直接运营（如社会补贴公交、地铁），或通过监管设定价格上限，亦或以平均成本定价为主，部分补贴边际成本亏损。

监管实践的挑战

监管自然垄断时，面临诸多实际障碍。最大的难点之一是成本核算，监管者需要尽量识别企业真实运营成本，以便合理设定价格，但企业往往有激励隐藏或夸大成本，导致信息不对称。此外，监管与政府直接运营在激励与效率方面各有利弊。

以中国为例，国家和地方发展改革部门普遍对电力、自来水、燃气、铁路等自然垄断行业实施价格监管，但在监管效果和执行难度上同样面临诸多挑战。

理想状态下，理论建议政府采用边际成本定价加“一次性固定补贴”弥补企业亏损，但实践中，平均成本定价因其简单与政治可接受性被广为采纳。

---

垄断产生的原因

最小有效规模

我们何时预判一个行业会由多个企业竞争、何时会演变为垄断？核心在于平均成本曲线与市场需求曲线之间的关系。最小有效规模（Minimum Efficient Scale, MES）指企业能够实现最低平均成本所需的最小产量。如果 $MES$ 很小，许多企业都可以达到，市场趋于竞争；如果 $MES$ 接近市场总需求，则只容许一两家甚至只有一家企业生存，容易形成垄断。

• 当 $MES \ll$ 市场需求，行业内企业可达最低成本而仍有足够空间，维持多个企业并存。
• 当 $MES \approx$ 市场需求，市场容量只够一两家企业达到效益最优，易出现自然垄断。

下表总结了不同情形下的市场结构预测：

这背后的原理即“技术决定论”：底层生产技术决定了平均成本曲线的变化方向，进而塑造了市场结构的根本样貌。

政策对市场规模的影响

市场规模的变动同样会影响垄断倾向。自由贸易政策扩大了潜在市场容量，使国内企业面临海外竞争，有效削弱了定价权，提高市场竞争性；反之，贸易保护收缩市场规模，容易滋生和强化垄断。

• 自由贸易促进了竞争，提升了效率，推动市场开放。
• 贸易保护则收缩了需求范围，降低了进入壁垒，加重垄断色彩。

随着全球化发展，许多曾经固守一地的垄断产业正逐步面临国际竞争压力，技术与市场环境变迁也在不断改变最小有效规模的门槛。

卡特尔与合谋

还有一种垄断形式，是多个企业通过合谋形成的。若行业内企业通过达成协议，共同限制产量以“抬高”价格，便形成了卡特尔（Cartel）。卡特尔让成员企业分享类似垄断者的利润，避免价格战，但也面临搭便车、监督与合规等实际困难。

• 合谋能阻止价格竞争、提升行业利润，却极易受到内部“背叛”、缺乏约束力的问题，以及政府反垄断执法的威慑。
• 法律风险高，监管部门如司法部反垄断司、联邦贸易委员会等会严厉查处，并处以巨额罚款。

除了合谋，垄断还可能由市场先发优势、巨大市场进入壁垒（如工具、资本准备）、以及历史路径依赖等偶然因素决定。最早进入的企业通常享有资源和经验积累，能够通过规模和降价威胁抑制后来者，形成事实上的垄断。

---

总结

垄断理论主要关注市场力量的来源、表现及其结果。在定价方面，垄断企业以“边际收入等于边际成本”为最优决策原则，定价权取决于需求弹性，加价定价公式恰反映了市场对价格变化的敏感程度。效率层面，垄断导致帕累托无效率和死重损失，社会福利相较于完全竞争减少。自然垄断的出现则源于成本结构的特殊性，需要特别的政府监管和政策干预。垄断的成因多样，既可能因为生产的最小有效规模过大，也可能由专利、许可、合谋以及企业先发优势等历史和策略性因素导致。

这些理论不仅指导了反垄断政策——如市场力量测算、合并审查与价格监控，也成为定价监管、公用事业投资与激励机制设计的理论基础。在创新与产业政策领域，垄断理论有助于分析专利保护期限、知识产权与市场效率的权衡，以及数字经济下市场结构与监管的新挑战。

近年来，数字平台和互联网巨头带来的“网络效应”、数据资源集中与平台经济垄断等新型问题，促使理论进一步关注算法定价、人工智能、双边市场和动态垄断的影响。同时，行为经济学的融入推动了对消费者偏见、注意力经济和垄断力量根源的新认识。