走入算法

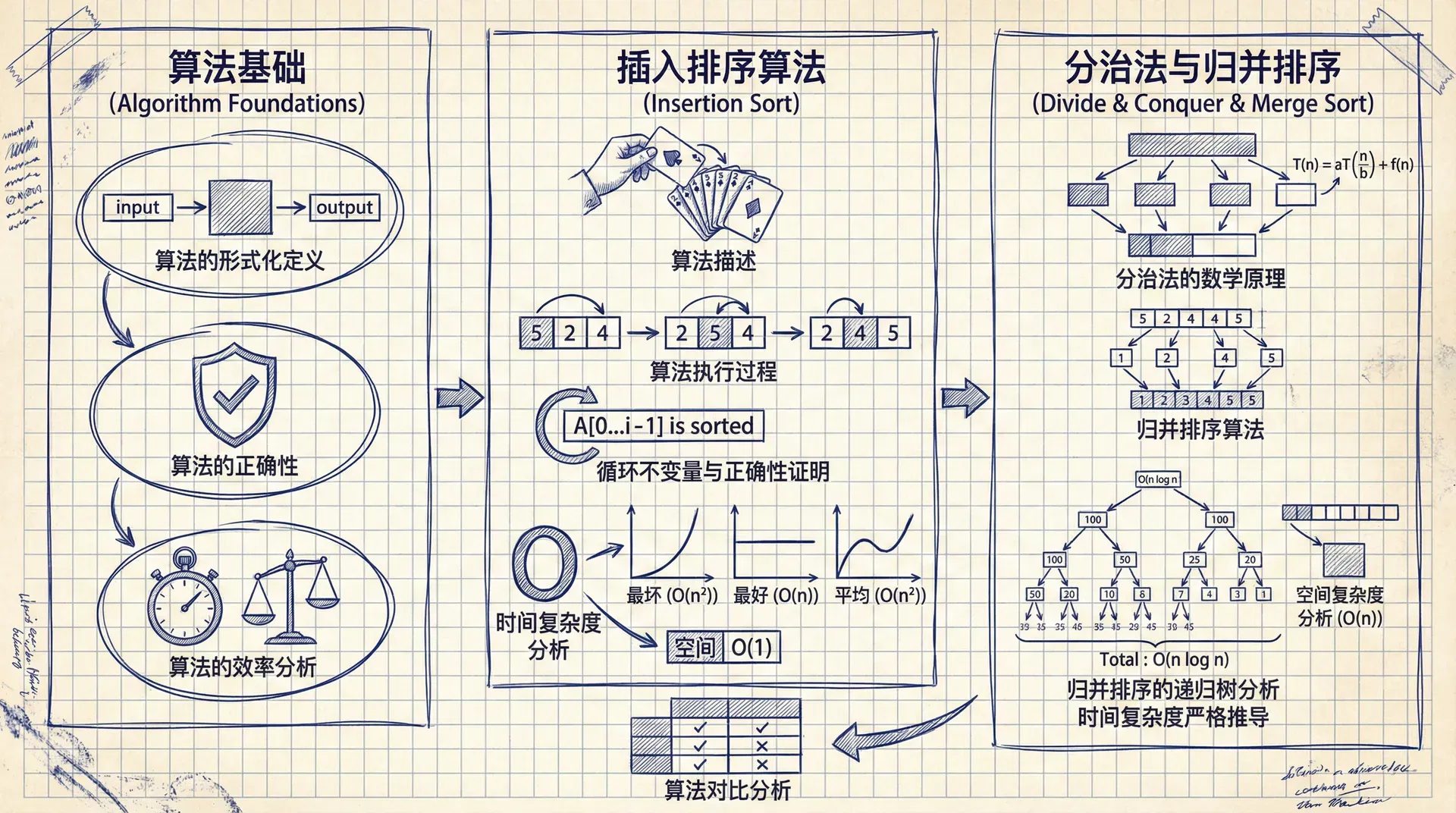
算法的形式化定义

在计算机科学中，算法是一个形式化的概念。我们可以将算法定义为：一个有限的、明确的、可执行的指令序列，用于解决特定问题或完成特定计算任务。

更严格地说，一个算法 $A$ 可以形式化地表示为：

$A = (I, O, P, S)$

其中：

• $I$ 表示输入集合，即算法接受的所有可能输入
• $O$ 表示输出集合，即算法产生的所有可能输出
• $P$ 表示前置条件（Precondition），定义了输入必须满足的约束
• $S$ 表示后置条件（Postcondition），定义了输出与输入之间的关系

算法的执行过程可以看作是一个从输入空间到输出空间的映射函数：$f: I \rightarrow O$，该函数满足前置条件 $P$ 和后置条件 $S$。

算法的正确性

算法的正确性是指算法能够满足其后置条件。形式化地，对于任意满足前置条件 $P$ 的输入 $x \in I$，算法 $A$ 必须产生满足后置条件 $S$ 的输出 $f(x) \in O$。

正确性证明通常采用数学归纳法或循环不变量技术。我们将在后续学习中详细讨论这些证明方法。

算法的效率分析

算法的效率通常通过计算复杂度来衡量。我们关注两个主要方面：

• 时间复杂度 $T(n)$：算法执行所需的基本操作次数，表示为输入规模 $n$ 的函数。我们通常使用渐进记号（如 $O$、$\Theta$、$\Omega$）来描述时间复杂度的增长趋势。
• 空间复杂度 $S(n)$：算法执行过程中所需的内存空间，同样表示为输入规模 $n$ 的函数。

对于大规模问题，不同复杂度的算法性能差异显著。例如，对于规模为 $n = 10^6$ 的排序问题：

• 时间复杂度为 $O(n \log n)$ 的算法可能在秒级完成
• 时间复杂度为 $O(n^2)$ 的算法可能需要小时级时间

这种差异促使我们深入研究算法设计，追求更优的复杂度上界。

插入排序算法

插入排序（Insertion Sort）是一种基于比较的排序算法，其核心思想是维护一个已排序的子数组，逐步将未排序的元素插入到正确位置。

算法描述

给定一个数组 $A[1..n]$，其中 $A[i]$ 表示数组的第 $i$ 个元素。插入排序算法的伪代码描述如下：

|
INSERTION-SORT(A)
1  for j = 2 to A.length                    // 从第二个元素开始处理
2      key = A[j]                           // 当前待插入的元素
3      i = j - 1                            // 已排序子数组的右边界索引
4      while i > 0 and A[i] > key           // 在已排序部分中寻找插入位置
5          A[i+1] = A[i]                    // 将大于key的元素向右移动
6          i = i 

算法执行过程

让我们通过一个具体实例来观察算法的执行过程。考虑数组 $A = [5, 2, 4, 6, 1, 3]$：

循环不变量与正确性证明

为了严格证明插入排序的正确性，我们使用循环不变量（Loop Invariant）技术。循环不变量是在循环的每次迭代前后都保持为真的性质。

循环不变量：在 INSERTION-SORT 的外层 for 循环的每次迭代开始时，子数组 $A[1..j-1]$ 包含原数组中位置 $1$ 到 $j-1$ 的元素，且这些元素已按非降序排列。

证明过程：

1. 初始化：当 $j=2$ 时，子数组 $A[1..1]$ 只包含一个元素，天然满足排序性质，循环不变量成立。
2. 保持：假设在第 $j$ 次迭代开始时，$A[1..j-1]$ 已排序。算法执行第 $4-7$ 行的内层循环，将 插入到 中的正确位置。由于插入操作保持了元素的相对顺序，迭代结束后 仍然有序，循环不变量得以保持。

根据数学归纳法原理，循环不变量在初始化、保持和终止三个阶段都成立，因此插入排序算法是正确的。

时间复杂度分析

我们采用渐进分析法来评估插入排序的时间复杂度。设 $n$ 为输入数组的长度。

最坏情况分析

最坏情况发生在输入数组完全逆序时，即 $A[1] > A[2] > \cdots > A[n]$。

对于每个 $j = 2, 3, \ldots, n$，元素 $A[j]$ 需要与 $A[j-1], A[j-2], \ldots, A[1]$ 进行比较，共 次比较。同时，每次比较后都需要执行一次元素移动操作。

总比较次数为： $C_{worst}(n) = \sum_{j=2}^{n} (j-1) = \sum_{i=1}^{n-1} i = \frac{n(n-1)}{2} = \Theta(n^2)$

总移动次数同样为 $\Theta(n^2)$。因此，最坏情况时间复杂度为 $T_{worst}(n) = \Theta(n^2)$。

最好情况分析

最好情况发生在输入数组已经有序时，即 $A[1] \leq A[2] \leq \cdots \leq A[n]$。

对于每个 $j = 2, 3, \ldots, n$，元素 $A[j]$ 只需与 $A[j-1]$ 比较一次即可确定其位置正确，无需移动元素。

总比较次数为： $C_{best}(n) = \sum_{j=2}^{n} 1 = n-1 = \Theta(n)$

总移动次数为 $0$（或常数次）。因此，最好情况时间复杂度为 $T_{best}(n) = \Theta(n)$。

平均情况分析

对于随机排列的输入数组，我们需要计算期望比较次数。

对于位置 $j$ 的元素 $A[j]$，它需要插入到 $A[1..j-1]$ 中的某个位置。由于输入是随机排列的，$A[j]$ 在 $A[1..j]$ 中处于任意位置的概率相等，即 。

因此，$A[j]$ 的期望比较次数为： $`E[C_j] = \frac{1}{j} \sum_{k=1}^{j-1} k = \frac{(j-1)j}{2j} = \frac{j-1}{2}`$

总期望比较次数为： $E[C_{avg}(n)] = \sum_{j=2}^{n} \frac{j-1}{2} = \frac{1}{2} \sum_{i=1}^{n-1} i = \frac{n(n-1)}{4} = \Theta(n^2)$

因此，平均情况时间复杂度为 $T_{avg}(n) = \Theta(n^2)$。

空间复杂度分析 —— 插入排序

插入排序是原地排序算法（In-place Sort），除了输入数组外，只需要常数个额外变量（如 key、i、j）。因此，空间复杂度为 $S(n) = \Theta(1)$。

分治法与归并排序

插入排序采用增量式方法，每次处理一个元素。相比之下，分治法（Divide-and-Conquer）是一种更强大的算法设计范式，它将问题分解为更小的子问题，递归求解后合并结果。

分治法的数学原理

分治法的核心思想可以形式化地描述为：对于问题规模为 $n$ 的实例，如果存在常数 $a \geq 1$、$b > 1$ 和 $d \geq 0$，使得：

1. 分解：将问题分解为 $a$ 个规模为 $n/b$ 的子问题
2. 解决：递归求解这些子问题
3. 合并：将子问题的解合并，合并操作的时间复杂度为 $\Theta(n^d)$

则问题的递归关系可以表示为： $T(n) = aT(n/b) + \Theta(n^d)$

根据主定理（Master Theorem），该递归式的解为：

归并排序算法

归并排序（Merge Sort）是分治法的经典应用。算法的核心思想是：将数组分成两半，分别排序后合并。

算法描述：

|
MERGE-SORT(A, p, r)
1  if p < r                              // 如果子数组包含多个元素
2      q = ⌊(p + r) / 2⌋                 // 计算中点，向下取整
3      MERGE-SORT(A, p, q)               // 递归排序左半部分 A[p..q]
4      MERGE-SORT(A, q+1, r)             // 递归排序右半部分 A[q+1..r]
5      MERGE(A, p, q, r)                 

合并操作：MERGE 过程将两个已排序的子数组 $A[p..q]$ 和 $A[q+1..r]$ 合并为一个有序数组。

|
MERGE(A, p, q, r)
1  n1 = q - p + 1                        // 左子数组长度
2  n2 = r - q                            // 右子数组长度
3  let L[1..n1+1] and R[1..n2+1] be new arrays  // 创建临时数组
4  for i = 1 to n1
5      L[i] = A[p 

哨兵值 $\infty$ 的使用确保了当其中一个子数组的元素全部被复制后，另一个子数组的剩余元素会自动被复制，简化了边界条件处理。

归并排序的递归树分析

归并排序的执行过程可以用递归树来可视化。对于规模为 $n$ 的数组：

递归树的深度为 $\lceil \log_2 n \rceil$，每一层的所有子问题合并操作的总时间复杂度为 $\Theta(n)$。因此，归并排序的总时间复杂度为 $T(n) = \Theta(n \log n)$。

时间复杂度严格推导

我们使用递归关系式来严格推导归并排序的时间复杂度。

设 $T(n)$ 表示对 $n$ 个元素进行归并排序的时间复杂度。根据算法描述：

这里，$2T(n/2)$ 表示递归求解两个规模为 $n/2$ 的子问题，$\Theta(n)$ 表示合并操作的时间复杂度。

展开递归式：

$T(n) = 2T(n/2) + cn$

其中 $c$ 是某个正常数。继续展开：

当 $n/2^k = 1$，即 $k = \log_2 n$ 时，递归到达基准情况：

$`T(n) = 2^{\log_2 n} T(1) + cn \log_2 n = n \cdot \Theta(1) + cn \log_2 n = \Theta(n \log n)`$

因此，归并排序的时间复杂度为 $T(n) = \Theta(n \log n)$，且在所有情况下（最好、平均、最坏）都保持这一复杂度。

空间复杂度分析

归并排序不是原地排序算法。在 MERGE 过程中，需要创建两个临时数组 $L$ 和 $R$，总长度为 $n$。递归调用栈的深度为 $\Theta(\log n)$，每层需要存储常数个变量。因此，空间复杂度为 $S(n) = \Theta(n)$。

算法对比分析

从理论角度对比插入排序和归并排序：

适用场景分析：

对于小规模数据（如 $n < 50$），插入排序的常数因子较小，实际性能可能优于归并排序。此外，插入排序是原地排序，在内存受限环境中具有优势。

对于大规模数据，归并排序的 $\Theta(n \log n)$ 复杂度明显优于插入排序的 $\Theta(n^2)$。当 $n = 10^6$ 时，归并排序的优势尤为显著。

对于几乎有序的数据，插入排序能够利用其最好情况的线性时间复杂度，性能接近 $\Theta(n)$，而归并排序仍然需要 $\Theta(n \log n)$ 时间。

小练习

4. 插入排序手动执行练习

对数组 [8, 3, 5, 4, 7, 6, 1, 2] 执行插入排序算法，详细记录每一步的数组状态和比较次数。

要求：逐步展示插入排序的过程，记录每次插入后的数组状态。

|
#include <iostream>
#include <vector>
#include <string>
 
void printArray(const std::vector<int>& arr) {
    std::cout << "[";
    for (size_t i = 0; i < arr.size(); i++) {
        std::cout << arr[i];

说明：

• 插入排序过程：
  • 从第二个元素开始，逐个将元素插入到已排序的子数组中
  • 每次插入需要比较和移动元素
  • 总比较次数：1+1+2+1+2+6+6 = 19次
• 时间复杂度：
  • 最好情况：O(n)，数组已排序
  • 最坏情况：O(n²)，数组完全逆序
  • 平均情况：O(n²)