函数的增长

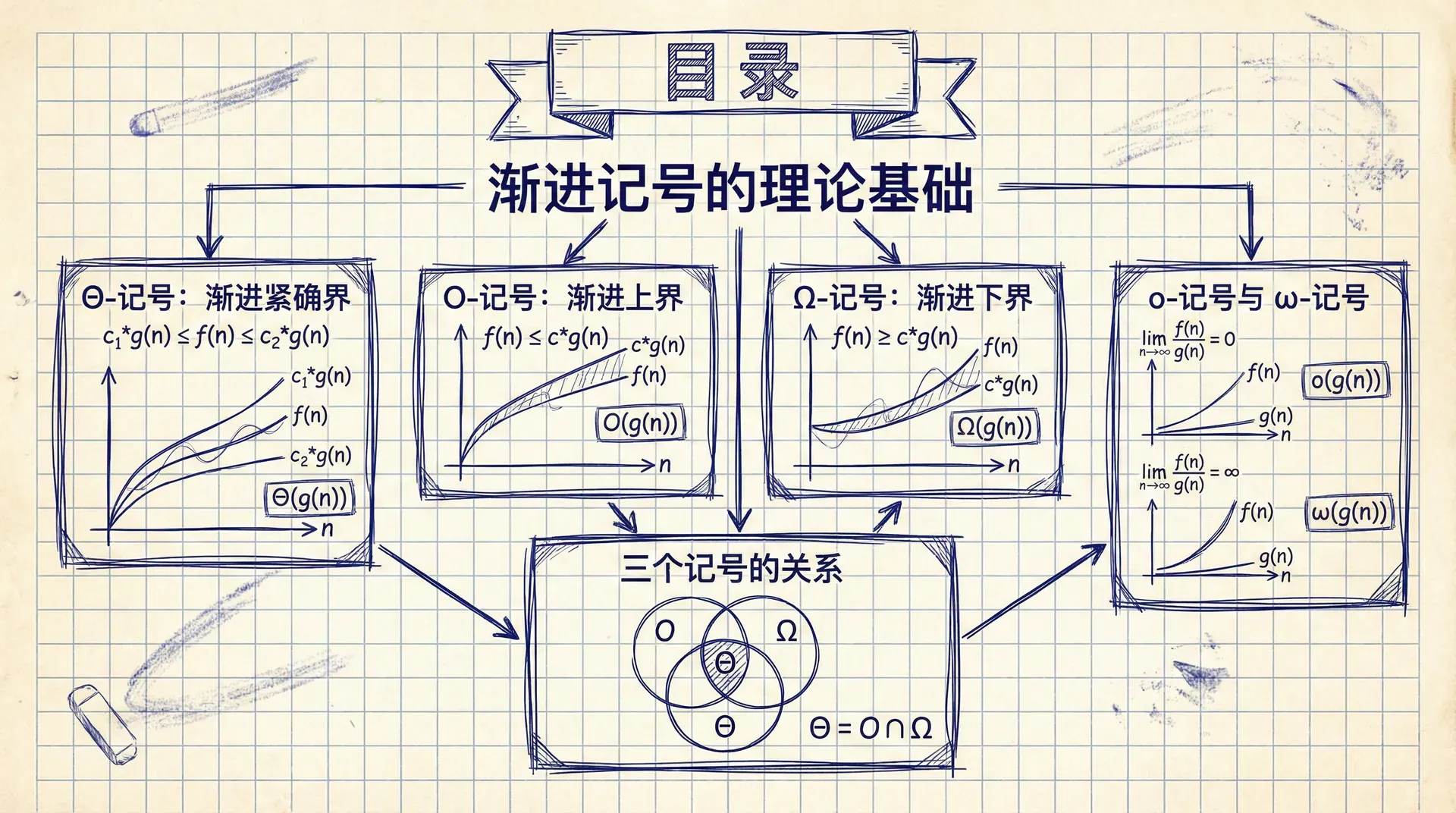
渐进记号的理论基础

渐进记号是算法分析中的核心数学工具，用于描述函数在输入规模趋于无穷大时的渐进行为。这些记号建立在极限理论的基础上，允许我们忽略常数因子和低阶项，专注于算法的本质特征。

在算法分析中，我们通常关注非负函数 $f: \mathbb{N} \to \mathbb{R}^+$ 的渐进行为，其中输入规模 $n$ 表示问题的规模。渐进记号提供了一种形式化的方法来比较不同函数的增长速度。

Θ-记号：渐进紧确界

Θ-记号（Theta记号）表示函数的渐进紧确界，它同时给出了函数的上界和下界。

形式化定义：设 $f(n)$ 和 $g(n)$ 为定义在正整数集上的函数。我们称 $f(n) = \Theta(g(n))$，当且仅当存在正常数 $c_1$、$c_2$ 和 $n_0$，使得对于所有 $n \ge n_0$，都有：

用逻辑符号表示为：

数学性质：

• 自反性：$f(n) = \Theta(f(n))$
• 对称性：若 $f(n) = \Theta(g(n))$，则 $g(n) = \Theta(f(n))$

证明示例：证明 $3n^2 + 2n + 1 = \Theta(n^2)$

O-记号：渐进上界

O-记号（大O记号）表示函数的渐进上界，用于描述算法在最坏情况下的性能上界。

形式化定义：设 $f(n)$ 和 $g(n)$ 为定义在正整数集上的函数。我们称 $f(n) = O(g(n))$，当且仅当存在正常数 $c$ 和 $n_0$，使得对于所有 ，都有：

用逻辑符号表示为：

数学性质：

• 自反性：$f(n) = O(f(n))$
• 传递性：若 $f(n) = O(g(n))$ 且 $g(n) = O(h(n))$，则

证明示例：证明 $2n + 3 = O(n)$

对于 $n \ge 3$，有 $2n + 3 \le 2n + n = 3n$。取 $c = 3$，$$，则 对所有 成立，因此 。

Ω-记号：渐进下界

Ω-记号（大Omega记号）表示函数的渐进下界，用于描述算法在最好情况下的性能下界。

形式化定义：设 $f(n)$ 和 $g(n)$ 为定义在正整数集上的函数。我们称 $f(n) = \Omega(g(n))$，当且仅当存在正常数 $c$ 和 $n_0$，使得对于所有 ，都有：

用逻辑符号表示为：

数学性质：

• 自反性：$f(n) = \Omega(f(n))$
• 传递性：若 $f(n) = \Omega(g(n))$ 且 $g(n) = \Omega(h(n))$，则

证明示例：证明 $n^2 + n = \Omega(n^2)$

对于 $n \ge 1$，有 $n^2 + n \ge n^2$。取 $c = 1$，，则 对所有 成立，因此 。

三个记号的关系

Θ-记号、O-记号和Ω-记号之间存在重要的数学关系。

定理：$f(n) = \Theta(g(n))$ 当且仅当 $f(n) = O(g(n))$ 且 $f(n) = \Omega(g(n))$。

证明：

o-记号与 ω-记号

o-记号和ω-记号提供了比O-记号和Ω-记号更严格的比较关系。

o-记号（小o记号）的形式化定义：$f(n) = o(g(n))$ 当且仅当：

等价地，对于任意正常数 $c > 0$，存在 $n_0 \in \mathbb{N}$，使得对所有 $n \ge n_0$，都有 。

ω-记号（小omega记号）的形式化定义：$f(n) = \omega(g(n))$ 当且仅当：

等价地，对于任意正常数 $c > 0$，存在 $n_0 \in \mathbb{N}$，使得对所有 $n \ge n_0$，都有 。

与O/Ω记号的关系：

• 若 $f(n) = o(g(n))$，则 $f(n) = O(g(n))$，但反之不成立
• 若 $f(n) = \omega(g(n))$，则 ，但反之不成立

证明示例：证明 $n = o(n^2)$

因此 $n = o(n^2)$。

常用函数的增长速度

在算法分析中，不同函数类型的增长速度存在严格的数学关系。我们通过极限理论可以严格证明这些函数的增长速度排序。

增长速度的严格排序

对于常见的函数类型，当 $n \to \infty$ 时，增长速度的严格排序为：

其中 $\prec$ 表示"增长速度严格慢于"。

数学证明（以 $\log n = o(n)$ 为例）：

应用洛必达法则：

因此 $\log n = o(n)$，即对数函数的增长速度严格慢于线性函数。

函数类型及其渐近性质

增长速度比较的数学分析

定理：对于任意常数 $a > 1$ 和 $b > 0$，有 $n^b = o(a^n)$。

证明：应用洛必达法则 $b$ 次：

因此多项式函数的增长速度严格慢于指数函数。

定理：对于任意常数 $a > 1$，有 $a^n = o(n!)$。

证明：使用斯特林公式 $n! \sim \sqrt{2\pi n} \left(\frac{n}{e}\right)^n$，可得：

因此指数函数的增长速度严格慢于阶乘函数。

渐进记号的性质与运算

渐进记号满足一系列重要的数学性质，这些性质在算法分析中具有重要应用。

基本运算性质

加法性质：

• 若 $f_1(n) = O(g_1(n))$ 且 $f_2(n) = O(g_2(n))$，则

乘法性质：

• 若 $f_1(n) = O(g_1(n))$ 且 $f_2(n) = O(g_2(n))$，则

标量乘法：对于任意常数 $c > 0$，$c \cdot f(n) = \Theta(f(n))$。

记号之间的关系

对偶关系：$f(n) = O(g(n))$ 当且仅当 $g(n) = \Omega(f(n))$。

包含关系：

• 若 $f(n) = o(g(n))$，则 $f(n) = O(g(n))$
• 若 $f(n) = \omega(g(n))$，则

练习

1. 严格证明以下等式的正确性：

   • 证明 $3n^2 + 2n + 1 = O(n^2)$，并给出具体的常数 $c$ 和 $n_0$

|
def mystery_function(n):
    result = 0
    for i in range(n):
        for j in range(i, n):
            for k in range(j, n):
                result += 1
    return result

要求：计算内层循环的执行次数，并用渐进记号表示结果。

4. 算法选择的理论分析： 在以下场景中，从理论角度分析应选择何种时间复杂度的算法，并说明理由：
   • 排序1000个用户ID（考虑常数因子和实际性能）
   • 在100万个文件中查找特定文件（考虑预处理成本）
   • 计算100个城市之间的最短路径（考虑问题规模与算法复杂度）
   • 验证一个100位数字是否为质数（考虑问题特性）