数组 | 自在学数组
想象你自己正站在一条笔直的街道上,这条街道上的每一栋房子都有着相同的结构,门牌号从0开始依次递增:0号、1号、2号、3号......每栋房子之间紧密相邻,没有任何空隙。
如果你知道某栋房子的门牌号,你就能立刻找到它的确切位置。这就是数组在计算机内存中的样子。
数组是我们将要学习的第一个具体数据结构,也是所有数据结构中最基础、最重要的一个。就像建造房屋需要从地基开始一样,理解数据结构也要从数组开始。
在接下来的学习中,我们会发现几乎所有复杂的数据结构,在它们的底层实现中,都能找到数组的身影。
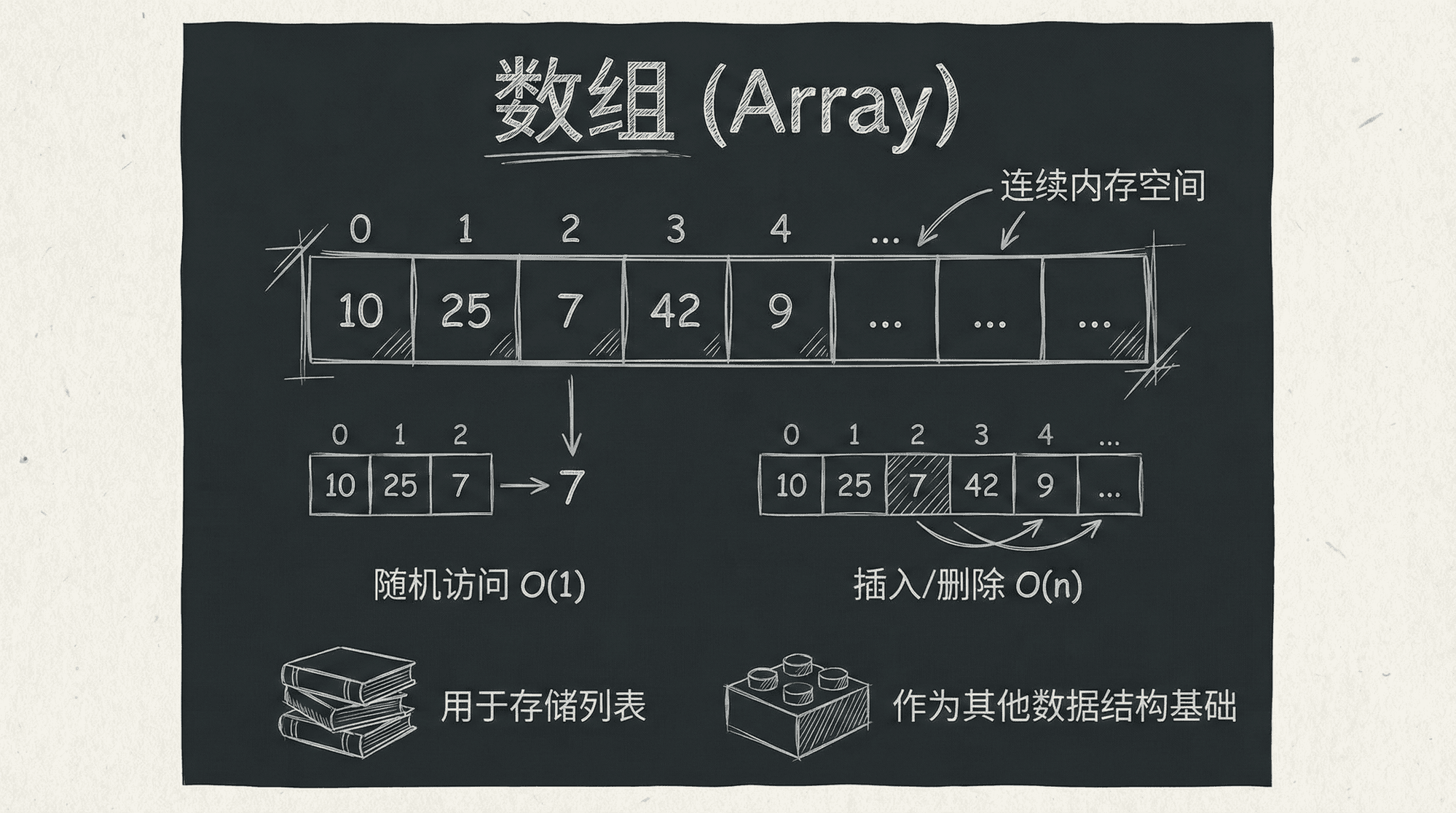
数组的本质
数组(Array)就像是内存中的一条整齐街道,有着三个重要的特征,正是这些特征让数组成为了计算机科学中最基础也最强大的数据结构:
- 数组具有同质性。就像一条街道上的所有房子都有着相同的结构和大小一样,数组中的每个元素都必须是相同的数据类型。
比如,一个整数数组里只能住着整数,一个字符数组里只能住着字符。这种同质性确保了每个“房子”(元素)占用的空间大小都是一样的。
- 数组具有线性特征。想象你沿着街道走,每栋房子都有明确的前后关系:除了第一栋房子,每栋房子都有一个确定的前面的邻居;
除了最后一栋房子,每栋房子都有一个确定的后面的邻居。数组中的元素也是这样排列的,形成了一条清晰的数据链条。
- 数组具有连续性。这就像街道上的房子是紧挨着建造的,中间没有任何空地一样。在计算机内存中,数组的元素也是紧密相邻地存放着,没有任何空隙。
正是这种连续性,赋予了数组最神奇的能力:我们可以通过一个简单的数学公式,瞬间找到任何一个元素的位置。
让我们用一个具体的例子来理解这个神奇的定位公式。假设我们有一个整数数组arr,第一个元素的内存地址是0x1000(这是一个十六进制地址),每个整数占用4个字节的空间。现在,如果我们想要找到第3个元素(索引为2,因为我们从0开始计数)的位置,计算过程就是:
Address(arr[2])=0x1000+2×4=0x1008
这个计算过程就像是我们在街道上找房子一样简单:知道了第一栋房子的地址,知道了每栋房子的宽度,我们就能立刻算出任何一栋房子的准确位置,而不需要从头开始一栋一栋地数。
正是因为这个公式只涉及一次乘法和一次加法运算,计算机可以在极短的时间内完成计算,直接跳转到目标元素的位置。这种能力被称为随机访问,它让数组访问任意元素的时间复杂度都是O(1)——无论数组有多大,访问任何一个元素的时间都是恒定的。
让我们看看如何在C++中创建和使用数组。C++为我们提供了两种主要的方式来创建固定大小的数组:
#include <iostream>
#include <array>
using namespace std;
void demonstrateArrays() {
// 方式一:传统的C风格数组
int traditional_array[5] = {10, 20, 30, 40, 50}; // 创建一个包含5个整数的数组
// 访问数组中的元素(索引从0开始)
cout << "传统数组的第3个元素是: " << traditional_array[2] <<
这两种数组都有一个重要特点:它们的大小必须在编译的时候就确定下来,就像建房子时必须先规划好要建多少个房间一样。一旦创建完成,数组的大小就不能再改变了。这些数组通常存储在程序的栈内存中,访问速度非常快。
数组的基本操作
现在让我们来探索在数组这条“街道”上可以进行哪些操作,以及每种操作需要花费多少时间和精力。
访问元素
访问数组中的元素就像知道确切地址后直接走到某栋房子一样简单。由于我们有那个神奇的地址计算公式,无论我们想访问第1个元素还是第100万个元素,所需的时间都是一样的。
#include <vector>
using namespace std;
void demonstrateAccess() {
vector<int> numbers = {10, 20, 30, 40, 50}; // 创建一个包含5个数字的数组
// 访问任意位置的元素都是瞬间完成的
int first_element = numbers[0]; // 获取第一个元素,值为10
int third_element = numbers[2];
这种访问操作的时间复杂度是O(1),这是数组最大的优势。
搜索元素
当我们想在数组中找到某个特定的值时,情况就不那么理想了。就像在一条街道上寻找某个特定的房子,但你只知道房子的外观而不知道门牌号一样,我们必须一个一个地检查,直到找到目标或者确认它不存在。
#include <vector>
using namespace std;
// 在数组中搜索指定的元素
int findElement(const vector<int>& arr, int target) {
// 从第一个元素开始,逐个检查
for (int i = 0; i < arr.size(); i++) { // 遍历数组中的每个位置
if (arr[i] == target) { // 检查当前位置的值是否是我们要找的
在最坏的情况下,我们要找的元素可能在数组的最后一个位置,或者根本不存在。这意味着我们需要检查数组中的每一个元素,所以搜索操作的时间复杂度是O(n)。
不过,如果数组是排好序的,我们就可以使用更聪明的二分查找方法(我们在大O表示法中介绍过),将时间复杂度降低到O(log n)——这就像在电话簿中查找姓名一样,我们可以不断地将搜索范围缩小一半。
插入元素
在数组中插入元素就像在一条已经建满房子的街道中间再加建一栋房子一样。由于数组要求所有元素必须紧密相邻,插入操作往往需要移动很多现有的元素。
如果我们只是在数组的末尾添加新元素,情况还比较简单,就像在街道的尽头新建一栋房子。但如果我们要在数组的中间或开头插入元素,就需要做大量的“搬迁”工作。
#include <vector>
using namespace std;
void demonstrateInsertion() {
vector<int> numbers = {10, 20, 30, 40, 50}; // 原始数组: [10, 20, 30, 40, 50]
// 情况1:在末尾插入(最简单的情况)
numbers.push_back(60); // 在末尾添加60
cout << "在末尾插入60后: ";
for (
当我们在数组的中间插入元素时,需要将插入位置后面的所有元素都向后移动一位。想象一下,如果我们要在一条有1000栋房子的街道的第2个位置插入一栋新房子,我们就需要将第2号到第1000号的所有房子都向后移动一个位置,这是一个非常耗时的过程。
在最坏的情况下(在数组开头插入),我们需要移动数组中的所有元素,因此插入操作的时间复杂度是O(n)。
删除元素
删除数组中的元素就像拆除街道上的一栋房子,然后需要让其他房子重新排列以填补空隙。
和插入操作类似,删除操作也需要维护数组元素的连续性。
#include <vector>
using namespace std;
void demonstrateDeletion() {
vector<int> numbers = {10, 20, 30, 40, 50, 60}; // 原始数组: [10, 20, 30, 40, 50, 60]
// 情况1:删除末尾元素(最简单的情况)
numbers.pop_back(); // 删除最后一个元素60
cout << "删除末尾元素后: ";
for (
当我们删除数组中间的某个元素时,就像拆除街道中间的一栋房子一样,我们需要让后面的所有房子向前移动一个位置来填补空隙。
如果我们删除的是第一个元素,那么除了第一个之外的所有元素都需要向前移动,这需要进行n-1次移动操作。
因此,删除操作的时间复杂度也是O(n)。
为什么插入和删除这么慢?
你可能会好奇:为什么数组的插入和删除操作需要这么多时间呢?答案就藏在数组的核心特性中——连续存储。
就像一条街道上的房子必须紧挨着建造一样,数组中的元素也必须在内存中紧密相邻。这种连续性虽然带来了快速随机访问的能力,但也意味着任何改变数组长度的操作都需要移动大量的元素来保持这种连续性。
这就像是一个权衡:我们用插入和删除的效率换取了访问的效率。在后面的学习中,我们会遇到链表这种数据结构,它做出了相反的选择——牺牲了随机访问的能力,但获得了O(1)时间复杂度的插入和删除操作。
数组操作实验室
动态数组
前面我们学习的静态数组就像是一条长度固定的街道——一旦建好了,就不能再增加或减少房子的数量。
但在实际编程中,我们经常需要一种能够根据需要自动增长的数组。这就是动态数组,在C++中最常用的实现就是std::vector。
vector的内部工作原理
std::vector看起来就像一个普通的数组,但它具有自动扩展的能力。这种“魔法”是如何实现的呢?
vector的秘密在于它维护了两个重要的信息:size(当前已经存储的元素数量)和capacity(当前已分配的内存空间能容纳的元素总数)。
你可以把它想象成一个聪明的房屋管理员,它不仅知道现在有多少居民(size),还知道现在总共准备了多少间房子(capacity)。
#include <vector>
#include <iostream>
using namespace std;
void understandVector() {
vector<int> numbers; // 创建一个空的vector
cout << "初始状态:" << endl;
cout << "size: " << numbers.size() << endl; // 当前元素数量,输出: 0
cout << "capacity: " << numbers.capacity() <<
当我们向vector中添加元素时,会发生以下两种情况之一:
情况一:还有剩余空间
如果当前的size小于capacity,也就是说还有空房间,那么添加新元素就很简单:直接把新元素放在下一个空位置上,然后将size加1。这个过程非常快,时间复杂度是O(1)。
情况二:空间已满,需要扩容
如果size等于capacity,也就是说所有房间都住满了,这时候就需要进行“街道扩建”:
首先,vector会申请一块更大的新内存空间,通常是当前容量的1.5倍到2倍。
然后,它会将所有现有的元素从旧的内存空间复制到新的内存空间中。最后,释放旧的内存空间,并在新空间中添加新元素。
扩容的代价分析
你可能会担心:既然扩容需要复制所有元素,那不是很慢吗?确实,单次扩容操作的时间复杂度是O(n),因为需要复制n个元素。但如果我们从长远的角度来看,情况就完全不同了。
让我们通过一个具体的例子来理解这个问题。假设我们要连续向一个空的vector中添加16个元素,看看总共需要进行多少次复制操作:
#include <vector>
#include <iostream>
using namespace std;
void analyzeVectorGrowth() {
vector<int> numbers;
int total_copies = 0; // 记录总的复制次数
for (int i = 1; i <= 16; i++) {
int old_capacity = numbers.capacity();
通过这个分析,我们会发现一个有趣的现象:虽然个别操作可能很昂贵(需要复制很多元素),但如果我们把成本分摊到所有操作上,平均成本是很低的。
这种分析方法叫做摊还分析。就像买房子一样,虽然首付款很高,但如果分摊到30年的房贷中,每个月的负担就变得可以接受了。
假设vector每次扩容都将容量翻倍,当我们连续添加n个元素时:大部分的添加操作都是简单的O(1)操作,只有在容量为1、2、4、8、16...的时候才会发生扩容。这些扩容操作复制的元素数量分别是0、1、2、4、8...,总的复制次数大约是n。
因此,n次添加操作的总时间成本约为:n次简单操作 + n次复制操作 = 2n。平均下来,每次添加操作的摊还时间复杂度就是O(1)。
这就是为什么std::vector在实际使用中非常高效的原因——虽然偶尔会有较慢的扩容操作,但从整体来看,添加元素的平均时间复杂度仍然是O(1)。
多维数组
到目前为止,我们讨论的都是一维数组,就像一条笔直的街道。但在现实世界中,我们经常需要处理更复杂的数据结构,比如表格、矩阵、甚至是三维空间中的数据。这时候,多维数组就派上用场了。
如果一维数组是一条街道,那么二维数组就像是一个住宅小区,有多条街道整齐地排列在一起。每个位置可以用两个坐标来确定:第几条街道(行),第几号房子(列)。
#include <vector>
#include <iostream>
using namespace std;
void demonstrateMultiDimensionalArrays() {
// 方式一:传统的二维数组(3行4列)
int traditional_matrix[3][4] = {
{1, 2, 3, 4}, // 第0行
{5, 6, 7, 8}, // 第1行
二维数组在内存中的存储方式
虽然我们在逻辑上把二维数组想象成一个表格,但在计算机内存中,它实际上仍然是线性存储的。计算机采用行主序的方式来存储二维数组,也就是说,它会先存储完第0行的所有元素,然后存储第1行的所有元素,以此类推。
这就像是把一个小区的所有房子按照“先完成第一条街,再完成第二条街”的顺序进行编号一样。这种存储方式对程序性能有重要影响,因为当我们按行访问数据时,相邻的内存位置会被连续访问,这对计算机的缓存系统非常友好。
无处不在的基础结构
数组就像建筑中的钢筋混凝土一样,虽然我们可能看不到它,但它构成了计算机科学中几乎所有复杂数据结构的基础。
许多我们后面将要学习的高级数据结构,比如栈、队列、哈希表、堆等,其底层实现都依赖于数组。
就像城市中的各种建筑,无论是住宅楼、办公楼还是商场,它们的地基都是相似的。
快速查找表
当我们需要根据某个整数键快速查找对应的值时,数组是最理想的选择。比如,如果我们要存储一年中每个月的天数,就可以用一个12元素的数组:
int daysInMonth[12] = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
// 想知道3月有多少天?直接访问daysInMonth[2]即可(注意从0开始计数)
矩阵运算的自然表示
在科学计算、图形学、机器学习等领域,矩阵运算是核心。二维数组为矩阵提供了最自然、最高效的表示方式。当我们需要处理图像(每个像素的颜色值)、神经网络的权重、或者3D图形的变换矩阵时,二维数组都是首选。
通过这一节课的学习,我们可以总结出数组的特点:
- 数组的超能力:数组最大的优势是其O(1)的随机访问能力。无论数组有多大,访问任意位置的元素都只需要相同的时间。这种能力加上连续内存布局带来的缓存友好性,使得数组在需要频繁随机访问数据的场景中无与伦比。
- 数组的限制:数组的主要限制在于插入和删除操作的高成本。由于需要维护元素的连续性,在数组中间插入或删除元素往往需要移动大量其他元素,时间复杂度达到O(n)。另外,静态数组的固定大小限制了其灵活性,而动态数组虽然可以自动扩容,但扩容过程可能带来性能波动。
小练习
- 在数组末尾添加一个元素(数组有足够空间)的时间复杂度是?
4. 数组内存地址计算练习
假设有一个整数数组 int[] arr = {10, 20, 30, 40, 50},数组的起始地址是 0x2000,每个整数占用 4 个字节。
arr[0] 的内存地址是多少?arr[3] 的内存地址是多少?- 如果我们知道
arr[2] 的地址是 0x2008,能推算出整个数组的起始地址吗?
答案:
arr[0] 的内存地址:0x2000(起始地址)arr[3] 的内存地址:0x2000 + 3 × 4 = 0x2000 + 12 = 0x200C- 如果知道
arr[2] 的地址是 0x2008:
- 起始地址 =
0x2008 - 2 × 4 = 0x2008 - 8 = 0x2000
说明:
- 数组元素在内存中是连续存储的
- 第 i 个元素的地址 = 起始地址 + i × 元素大小
- 如果知道某个元素的地址,可以通过公式反推起始地址
5. 数组操作的时间复杂度分析练习
分析以下每个操作的时间复杂度,并说明理由:
- 操作A:查找数组中的最大值
- 操作B:访问数组的第 k 个元素
- 操作C:在数组末尾添加元素(数组有足够空间)
- 操作D:在数组开头插入元素
#include <iostream>
#include <vector>
#include <sstream>
using namespace std;
// 操作A:查找数组中的最大值 - 时间复杂度 O(n)
int findMax(const vector<int>& arr)
{
int maxVal = arr[0];
for (int i = 1; i < arr.size(); i
6. 实现数组操作函数练习
实现以下函数,并分析它们的时间复杂度:
- 函数1:反转数组(使用双指针技巧)
- 函数2:在指定位置插入元素(不使用
List<T> 的 Insert 方法,手动实现)
#include <iostream>
#include <vector>
#include <sstream>
#include <stdexcept>
using namespace std;
// 函数1:反转数组 - 时间复杂度 O(n)
void reverseArray(vector<int>& arr)
{
int left = 0;
int right = arr.size() - 1;
7. 简单的井字棋游戏练习
设计并实现一个简单的井字棋(Tic-Tac-Toe)游戏:
- 使用二维数组表示 3×3 的棋盘
- 实现初始化棋盘、下棋、检查获胜、打印棋盘等功能
- 分析访问棋盘上任意位置和检查获胜条件的时间复杂度
#include <iostream>
#include <vector>
using namespace std;
class TicTacToe
{
private:
vector<vector<char>> board; // 3x3的游戏板
public:
TicTacToe()
{
// 初始化3x3的棋盘,用空格表示空位
board = vector<vector<char>>(3, vector<char>(
endl;
// 输出30
// 方式二:现代C++的std::array(更推荐使用)
array<int, 5> modern_array = {11, 22, 33, 44, 55}; // 创建一个std::array
// std::array提供了更多安全特性和便利方法
cout << "现代数组的第3个元素是: " << modern_array[2] << endl; // 输出33
cout << "现代数组的大小是: " << modern_array.size() << endl; // 输出5
// 我们可以安全地访问数组元素
cout << "使用at()方法访问: " << modern_array.at(2) << endl; // 更安全的访问方式
}
// 获取第三个元素,值为30
int last_element = numbers[4]; // 获取最后一个元素,值为50
cout << "第一个元素: " << first_element << endl; // 输出: 第一个元素: 10
cout << "第三个元素: " << third_element << endl; // 输出: 第三个元素: 30
cout << "最后一个元素: " << last_element << endl; // 输出: 最后一个元素: 50
}
return i; // 找到了!返回这个位置的索引
}
}
return -1; // 遍历完所有元素都没找到,返回-1表示不存在
}
void demonstrateSearch() {
vector<int> numbers = {15, 3, 9, 1, 7, 12, 6}; // 一个无序的数组
int position = findElement(numbers, 7); // 搜索数字7
if (position != -1) {
cout << "找到了数字7,它在位置 " << position << endl; // 输出: 找到了数字7,它在位置 4
} else {
cout << "没有找到数字7" << endl;
}
int missing_position = findElement(numbers, 100); // 搜索不存在的数字100
if (missing_position != -1) {
cout << "找到了数字100,它在位置 " << missing_position << endl;
} else {
cout << "没有找到数字100" << endl; // 这行会被执行
}
}
int
num : numbers) {
cout << num << " "; // 输出: 10 20 30 40 50 60
}
cout << endl;
// 情况2:在中间插入(需要移动元素)
// 比如我们想在位置2插入25,最终结果应该是[10, 20, 25, 30, 40, 50, 60]
numbers.insert(numbers.begin() + 2, 25); // 在索引2的位置插入25
cout << "在位置2插入25后: ";
for (int num : numbers) {
cout << num << " "; // 输出: 10 20 25 30 40 50 60
}
cout << endl;
}
// 让我们手动实现插入逻辑来理解背后发生了什么
void manualInsert(vector<int>& arr, int position, int value) {
// 首先扩展数组大小
arr.resize(arr.size() + 1);
// 从后往前移动元素,为新元素腾出空间
for (int i = arr.size() - 1; i > position; i--) {
arr[i] = arr[i - 1]; // 将每个元素向后移动一位
}
// 在指定位置插入新元素
arr[position] = value;
}
int
num : numbers) {
cout << num << " "; // 输出: 10 20 30 40 50
}
cout << endl;
// 情况2:删除中间元素(需要移动其他元素)
// 删除位置2的元素(值为30),最终结果应该是[10, 20, 40, 50]
numbers.erase(numbers.begin() + 2); // 删除索引2位置的元素
cout << "删除位置2的元素后: ";
for (int num : numbers) {
cout << num << " "; // 输出: 10 20 40 50
}
cout << endl;
}
// 让我们手动实现删除逻辑来理解背后的过程
void manualDelete(vector<int>& arr, int position) {
// 检查位置是否有效
if (position < 0 || position >= arr.size()) {
cout << "删除位置无效!" << endl;
return;
}
// 将后面的元素向前移动,覆盖要删除的元素
for (int i = position; i < arr.size() - 1; i++) {
arr[i] = arr[i + 1]; // 将后一个元素移动到当前位置
}
// 缩小数组大小
arr.resize(arr.size() - 1);
}
endl;
// 当前容量,可能输出: 0
// 添加一些元素,观察size和capacity的变化
for (int i = 1; i <= 10; i++) {
numbers.push_back(i);
cout << "添加元素 " << i << " 后 - size: " << numbers.size()
<< ", capacity: " << numbers.capacity() << endl;
}
}
numbers.
push_back
(i);
int new_capacity = numbers.capacity();
if (new_capacity > old_capacity) {
// 发生了扩容,计算复制的元素数量
int copies = i - 1; // 之前的所有元素都被复制了
total_copies += copies;
cout << "添加元素 " << i << " 时发生扩容,复制了 " << copies << " 个元素" << endl;
cout << "容量从 " << old_capacity << " 增长到 " << new_capacity << endl;
}
}
cout << "总共添加了 16 个元素,总复制次数: " << total_copies << endl;
cout << "平均每次添加操作的复制次数: " << (double)total_copies / 16 << endl;
}
{9, 10, 11, 12} // 第2行
};
// 访问第2行第3列的元素(注意从0开始计数)
cout << "传统数组[1][2] = " << traditional_matrix[1][2] << endl; // 输出: 7
// 方式二:使用vector创建动态二维数组
// 创建一个3行4列的二维数组,初始值都为0
vector<vector<int>> dynamic_matrix(3, vector<int>(4, 0));
// 填充一些数据
int value = 1;
for (int row = 0; row < 3; row++) {
for (int col = 0; col < 4; col++) {
dynamic_matrix[row][col] = value++; // 依次填入1,2,3...
}
}
// 访问和修改元素
dynamic_matrix[1][2] = 100; // 修改第2行第3列的元素
// 打印整个矩阵
cout << "动态二维数组:" << endl;
for (int row = 0; row < dynamic_matrix.size(); row++) {
for (int col = 0; col < dynamic_matrix[row].size(); col++) {
cout << dynamic_matrix[row][col] << "\t";
}
cout << endl;
}
}
++
)
// 需要遍历所有元素
{
if (arr[i] > maxVal)
{
maxVal = arr[i];
}
}
return maxVal;
}
// 时间复杂度:O(n)
// 原因:需要遍历数组中的所有 n 个元素
// 操作B:访问数组的第 k 个元素 - 时间复杂度 O(1)
int getElement(const vector<int>& arr, int k)
{
return arr[k]; // 直接通过索引访问
}
// 时间复杂度:O(1)
// 原因:数组支持随机访问,可以通过起始地址和索引直接计算出元素位置
// 操作C:在数组末尾添加元素(数组有足够空间)- 时间复杂度 O(1)
void addToEnd(vector<int>& list, int value)
{
list.push_back(value); // 直接添加到末尾
}
// 时间复杂度:O(1)(平均情况,如果数组有足够空间)
// 原因:不需要移动其他元素,只需要在末尾添加
// 操作D:在数组开头插入元素 - 时间复杂度 O(n)
void addToBeginning(vector<int>& list, int value)
{
list.insert(list.begin(), value); // 在开头插入
}
// 时间复杂度:O(n)
// 原因:需要将后面的所有元素向后移动一位
// 辅助函数:打印 vector
string vectorToString(const vector<int>& vec)
{
if (vec.empty()) return "[]";
stringstream ss;
ss << "[";
for (size_t i = 0; i < vec.size(); i++)
{
ss << vec[i];
if (i < vec.size() - 1) ss << ", ";
}
ss << "]";
return ss.str();
}
int main()
{
vector<int> arr = { 3, 1, 4, 1, 5, 9, 2, 6 };
cout << "最大值: " << findMax(arr) << endl;
cout << "第3个元素: " << getElement(arr, 3) << endl;
vector<int> list = { 1, 2, 3 };
addToEnd(list, 4);
cout << "末尾添加后: " << vectorToString(list) << endl;
addToBeginning(list, 0);
cout << "开头插入后: " << vectorToString(list) << endl;
return 0;
}
- 操作A(FindMax):时间复杂度 O(n)
- 操作B(GetElement):时间复杂度 O(1)
- 数组支持随机访问,可以通过起始地址和索引直接计算出元素位置
- 操作C(AddToEnd):时间复杂度 O(1)(平均情况)
- 如果数组有足够空间,直接添加到末尾,不需要移动其他元素
- 如果数组需要扩容,可能需要 O(n) 时间
- 操作D(AddToBeginning):时间复杂度 O(n)
- 需要将后面的所有元素向后移动一位,为插入的元素腾出空间
// 双指针技巧:从两端向中间交换
while (left < right)
{
// 交换左右两端的元素
int temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
left++;
right--;
}
}
// 时间复杂度:O(n)
// 原因:需要遍历数组的一半长度,执行 n/2 次交换操作
// 函数2:在指定位置插入元素 - 时间复杂度 O(n)
void insertAt(vector<int>& list, int index, int value)
{
if (index < 0 || index > static_cast<int>(list.size()))
{
throw out_of_range("索引超出范围");
}
// 手动实现插入:将后面的元素向后移动
list.push_back(0); // 先添加一个占位元素,扩大数组
// 从后往前移动元素
for (int i = list.size() - 1; i > index; i--)
{
list[i] = list[i - 1];
}
// 在指定位置插入新元素
list[index] = value;
}
// 时间复杂度:O(n)
// 原因:需要将 index 位置后面的所有元素向后移动一位
// 最坏情况(在开头插入)需要移动 n 个元素
// 辅助函数:打印 vector
string vectorToString(const vector<int>& vec)
{
if (vec.empty()) return "[]";
stringstream ss;
ss << "[";
for (size_t i = 0; i < vec.size(); i++)
{
ss << vec[i];
if (i < vec.size() - 1) ss << ", ";
}
ss << "]";
return ss.str();
}
int main()
{
// 测试反转数组
vector<int> arr = { 1, 2, 3, 4, 5 };
cout << "原数组: " << vectorToString(arr) << endl;
reverseArray(arr);
cout << "反转后: " << vectorToString(arr) << endl;
// 测试插入元素
vector<int> list = { 10, 20, 30, 40 };
cout << "\n原列表: " << vectorToString(list) << endl;
insertAt(list, 2, 25);
cout << "在索引2插入25后: " << vectorToString(list) << endl;
return 0;
}
原数组: [1, 2, 3, 4, 5]
反转后: [5, 4, 3, 2, 1]
原列表: [10, 20, 30, 40]
在索引2插入25后: [10, 20, 25, 30, 40]
- 函数1(ReverseArray):
- 时间复杂度:O(n)
- 使用双指针技巧,从两端向中间交换元素
- 需要执行 n/2 次交换操作
- 函数2(InsertAt):
- 时间复杂度:O(n)
- 需要将 index 位置后面的所有元素向后移动一位
- 最坏情况(在开头插入)需要移动 n 个元素
- 这就是为什么在数组开头插入比在末尾添加慢的原因
3
,
' '
));
}
// 在指定位置下棋
bool makeMove(int row, int col, char player)
{
// 检查位置是否有效
if (row < 0 || row >= 3 || col < 0 || col >= 3)
{
return false;
}
// 检查位置是否为空
if (board[row][col] != ' ')
{
return false;
}
// 下棋
board[row][col] = player;
return true;
}
// 检查是否有玩家获胜
char checkWinner()
{
// 检查行
for (int i = 0; i < 3; i++)
{
if (board[i][0] != ' ' && board[i][0] == board[i][1] && board[i][1] == board[i][2])
{
return board[i][0];
}
}
// 检查列
for (int j = 0; j < 3; j++)
{
if (board[0][j] != ' ' && board[0][j] == board[1][j] && board[1][j] == board[2][j])
{
return board[0][j];
}
}
// 检查主对角线
if (board[0][0] != ' ' && board[0][0] == board[1][1] && board[1][1] == board[2][2])
{
return board[0][0];
}
// 检查副对角线
if (board[0][2] != ' ' && board[0][2] == board[1][1] && board[1][1] == board[2][0])
{
return board[0][2];
}
// 没有获胜者
return ' ';
}
// 打印棋盘
void printBoard()
{
cout << " 0 1 2" << endl;
for (int i = 0; i < 3; i++)
{
cout << i << " ";
for (int j = 0; j < 3; j++)
{
cout << board[i][j];
if (j < 2) cout << " | ";
}
cout << endl;
if (i < 2) cout << " -----------" << endl;
}
}
};
int main()
{
TicTacToe game;
cout << "初始棋盘:" << endl;
game.printBoard();
// 模拟游戏过程
game.makeMove(0, 0, 'X');
game.makeMove(1, 1, 'O');
game.makeMove(0, 1, 'X');
game.makeMove(1, 0, 'O');
game.makeMove(0, 2, 'X');
cout << "\n游戏进行中:" << endl;
game.printBoard();
char winner = game.checkWinner();
if (winner != ' ')
{
cout << "\n获胜者: " << winner << endl;
}
return 0;
}
- 访问棋盘上任意位置的时间复杂度:O(1)
- 二维数组支持随机访问,可以通过
board[row, col] 直接访问任意位置
- 检查获胜条件的时间复杂度:O(1)
- 对于 3×3 的棋盘,需要检查 3 行、3 列、2 条对角线,总共 8 种情况
- 每种情况的检查都是常数时间,所以总时间复杂度是 O(1)
- 如果棋盘大小是 n×n,时间复杂度会是 O(n)
- 使用二维数组的优势:
- 直观地表示二维结构(棋盘)
- 支持 O(1) 的随机访问
- 内存布局连续,缓存友好
- 代码简洁易读
