链表
在上一部分中，我们介绍了数组结构，其物理存储上一块连续的内存区域，使得元素可以通过索引实现 O(1) 的随机访问。但数组在插入和删除操作时，尤其是在中间位置，往往需要移动大量元素，导致效率较低。
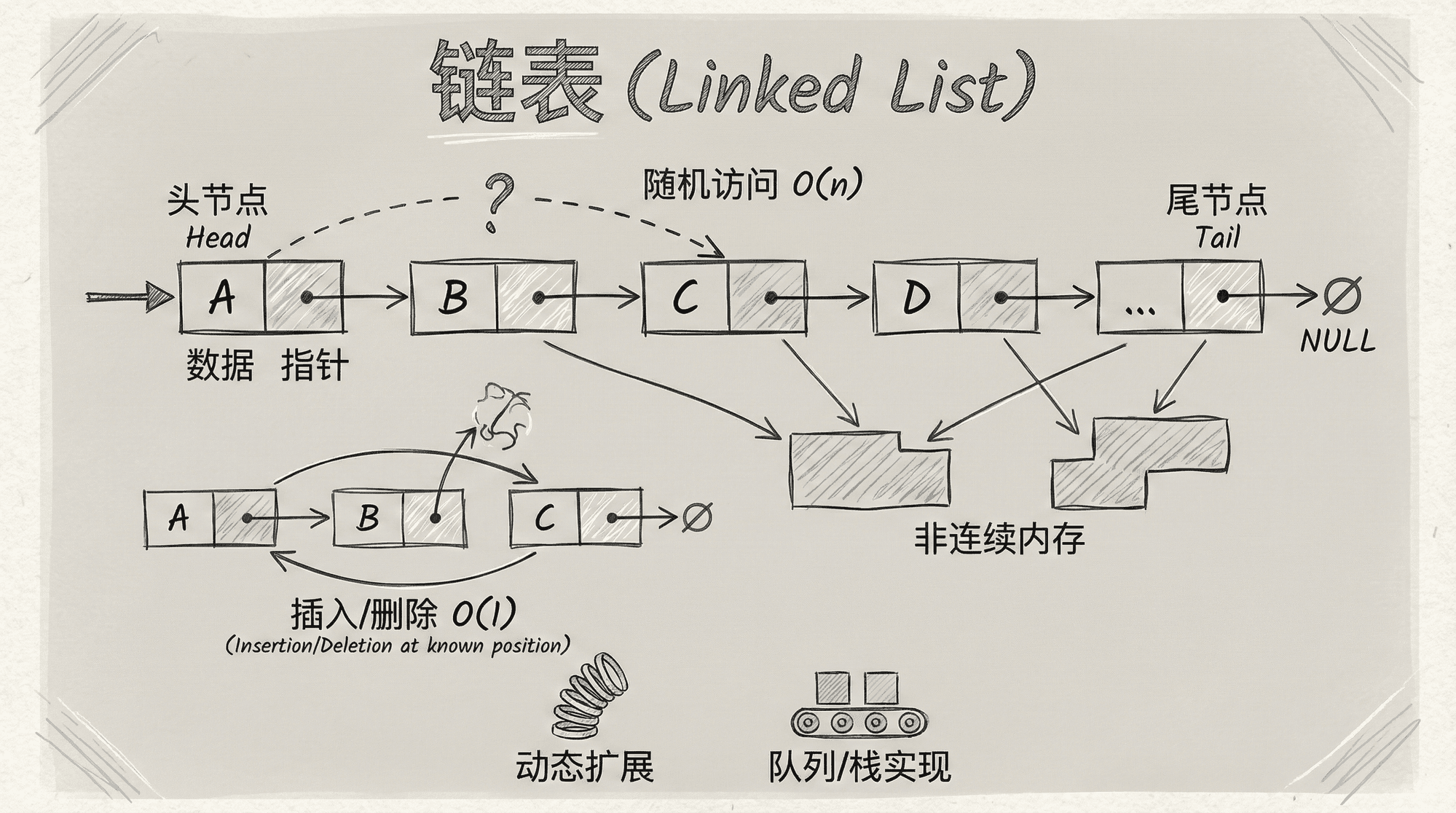
这节课我们将讨论另一种基础数据结构—— 链表（Linked List）。链表将数据元素封装在一系列称为 节点（Node） 的结构体中，每个节点包含数据域和一个指向下一个节点的指针域。 通过指针，链表的各个节点在内存中“串联”起来，但它们的物理地址可以是任意且不连续的。
链表的首节点由一个称为“头指针（head）”的变量进行管理。每个节点依靠指针域记录下一个节点的内存地址，最后一个节点的指针域指向空（如 nullptr 或 null），表示链表的终止。
由于链表节点的插入和删除操作仅需修改相邻节点的指针，无需大规模移动数据，因此在需要频繁动态增删元素的场景下，链表具有显著的优势。
链表（Linked List）由一系列 节点（Node） 构成，每个节点在内存中的位置可以是任意的，节点之间无需物理相邻。
这些节点通过指针域（通常称为 next 指针）连接在一起，指针域保存了下一个节点的内存地址，实现节点间的动态关联，从而形成数据结构上的有序链式序列。
一个最基本的节点包含两个核心部分：
- 数据域（Data）：存放我们真正关心的信息。
- 指针域（Pointer）：存放指向下一个节点的“箭头”，我们通常叫它
next指针。
在链表的数据结构中，遍历的起点由 头指针（Head） 标识，即指向链表第一个节点的指针。整个链表的链接通过各节点间的 next 指针实现。当某一节点的 next 指针为 nullptr（空指针）时，即表明链表到达终止位置，后续无更多节点。
单向链表
我们最先接触的，也是最基础的链表，叫做 单向链表（Singly Linked List）。就像它的名字一样，这是一条单行道，我们只能顺着它的链路一路向前，无法回头。
定义节点结构体
在使用 C++ 构建链表前，我们首先需要明确定义节点（Node）的数据结构。一个通用的链表节点应支持存储任意数据类型的信息——这既可以是数值、字符串，也可以是用户自定义的复杂类型。
#include <iostream>
// 我们用模板来定义一个通用的节点——节点
template <typename T>
struct Node {
T data; // 数据域：存放数据
Node* next; // 指针域：指向下一个节点的“箭头”
// 构造函数，当我们创建一个新的节点时调用
Node(T value) {
data = value; // 把数据放进数据域
next = nullptr; // 刚创建时，我们还不知道下一个节点在哪，所以 next 指针暂时指向空
}
};这个 Node 结构体就是我们链表的基本组成单位。它非常纯粹，只关心两件事：我身上带着什么数据？我的下一个节点在哪里？
创建链表管理器
在 C++ 中，链表的管理通常通过一个称为 链表类（LinkedList） 的结构体实现。这个类将负责维护链表的头指针，并提供一系列方法来操作链表，如插入、删除和遍历。
template <typename T>
class LinkedList {
private:
Node<T>* head; // 这是最重要的东西：指向第一个节点的头指针
public:
// 构造函数：链表刚开始时，我们手里什么节点都没有
LinkedList() {
head = nullptr; // 所以头指针指向空
}
// 析构函数：当链表被销毁时，需要把所有节点都清理干净
~LinkedList() {
Node<T>* current = head; // 从第一个节点开始
while (current != nullptr) {
Node<T>* nextNode = current->next; // 提前记下下一个节点的位置
delete current; // 释放当前节点的内存
current = nextNode; // 移动到下一个节点
}
std::cout << "链表已销毁，所有节点都已清理！" << std::endl;
}
// ... 我们将在这里添加各种管理链表的方法 ...
};请特别注意析构函数 ~LinkedList()。由于我们的节点都是用 new 在内存中动态创建的，
如果链表对象被销毁时不手动清理节点，这些节点就会变成无人认领的“内存垃圾”，永远留在那里，直到程序关闭。这种现象叫做内存泄漏，是我们编写 C++ 程序时尤其需要注意的点。
链表的基本操作
现在，让我们来实现链表的核心操作：插入、删除和查找。
插入节点
在链表头部插入新节点 是链表最高效的操作之一。
// 在 LinkedList 类中添加这个方法
void insertAtHead(T value) {
// 步骤1：制作一张新的线索纸条
Node<T>* newNode = new Node<T>(value);
std::cout << "得到一张新线索，写着 '" << value << "'" << std::endl;
// 步骤2：让新纸条的箭头指向原来的第一张纸条
newNode->next = head;
// 步骤3：更新游戏起点的标志，让它指向这张最新的纸条
head = newNode;
}在链表头部插入新节点的操作非常高效。无论链表长度如何（即节点数量多少），该操作仅涉及对头指针的简单修改，不依赖于链表规模。因此，其时间复杂度为 O(1)，可以在常数时间内完成。
尾部插入新节点（在链表末尾添加元素） 是另一种常见需求。此时，需要从头节点出发，遍历链表以找到当前的最后一个节点（其 next 指针为 nullptr），然后将新节点链接在其后。
// 在 LinkedList 类中添加这个方法
void insertAtTail(T value) {
// 步骤1：同样，先创建一个新节点
Node<T>* newNode = new Node<T>(value);
std::cout << "在路线末尾增加一张新线索 '" << value << "'" << std::endl;
// 如果链表是空的，那这个新节点就是第一个节点
if (head == nullptr) {
head = newNode;
return;
}
// 步骤2：从起点出发，沿着链表一直走到最后
Node<T>* current = head;
while (current->next != nullptr) { // 只要下一个节点不是 nullptr
current = current->next; // 就继续前进
}
// 步骤3：现在 current 指向了最后一个节点，让它的 next 指针指向我们的新节点
current->next = newNode;
}这个操作的成本就比较高了。因为我们必须从头到尾遍历一次链表，如果链表有 n 个节点，我们就需要走 n-1 步。所以，它的时间复杂度是 O(n)。
思考：有没有办法让尾部插入也变得飞快？
当然有！聪明的做法是在我们的链表管理器里，除了记录 head（起点），再增加一个 tail 指针，永远指向最后一个节点。
这样，每次在尾部添加新节点时，我们只需要操作 tail 指针，然后让 tail 指向新的结尾即可。这样一来，尾部插入的时间复杂度就从 O(n) 变成了 O(1)！这是一个非常常见的优化技巧。
删除节点
从链表头部删除节点 是另一种常见的操作。它的时间复杂度为 O(1)，因为只需修改头指针即可。
// 在 LinkedList 类中添加这个方法
void deleteFromHead() {
// 如果游戏还没开始，就什么都不做
if (head == nullptr) {
std::cout << "游戏还没开始，无法移除线索！" << std::endl;
return;
}
std::cout << "移除了第一张线索，内容是 '" << head->data << "'" << std::endl;
// 步骤1：临时记住原来的起点
Node<T>* oldHead = head;
// 步骤2：将游戏的起点更新为原来的第二张纸条
head = head->next;
// 步骤3：彻底销毁原来的那张纸条，防止内存泄漏
delete oldHead;
}和头部插入一样，这个操作也只涉及起点位置的指针改动，与链表长度无关。时间复杂度同样是 O(1)。
移除中间的某张线索（按值删除）, 这是链表操作中最需要小心的地方。假设我们要移除一张写着特定信息（比如“B”）的纸条。我们不能直接把它销毁，因为这会导致线索链断裂。 正确的做法是，找到“B”的前一个节点（“A”），然后让“A”的 next 指针直接指向“B”的下一个节点（“C”），从而把“B”完美地“架空”。
// 在 LinkedList 类中添加这个方法
void deleteValue(T value) {
if (head == nullptr) return; // 游戏未开始
// 特殊情况：如果第一张就是要删除的线索
if (head->data == value) {
deleteFromHead();
return;
}
// 从起点开始，寻找要删除的线索的前一张
Node<T>* prev = nullptr;
Node<T>* current = head;
while (current != nullptr && current->data != value) {
prev = current; // `prev` 紧跟在 `current` 后面
current = current->next; // `current` 向前探索
}
// 如果 `current` 不是 nullptr，说明我们找到了目标
if (current != nullptr) {
std::cout << "找到了线索 '" << value << "'，准备将其移除..." << std::endl;
// 步骤1：让前一张纸条的箭头，指向目标纸条的下一张
prev->next = current->next;
// 步骤2：现在目标纸条已经被“架空”，可以安全地销毁了
delete current;
} else {
std::cout << "没找到写着 '" << value << "' 的线索。" << std::endl;
}
}为了完成这个操作，我们同样需要从头开始遍历，所以在最坏的情况下，时间复杂度是 O(n)。 这也凸显了单向链表的一个特点：要操作一个节点，必须先找到它的前一个节点，我们才能进行操作。
一些特殊的链表
双向链表
单向链表的单行道特性意味着我们永远无法后退。如果我们在遍历途中想知道“我是从哪个节点过来的？”，我们只能回到起点重走一遍。为了解决这个问题，双向链表（Doubly Linked List） 诞生了。
在双向链表中，每个节点都变得更强大了。它不仅有一个指向下一个节点的 next 指针，还有一个指向上一个节点的 prev 指针。
- 节点结构:
(prev, data, next) - 起点
head的prev指针指向nullptr。 - 终点
tail的next指针指向nullptr。
双向链表的优势：
双向链表最大的好处在于，如果我们想删除一个节点，并且我们已经拿到了这个节点（有一个指向该节点的指针），删除操作会变得异常简单。我们不需要再从头遍历去寻找它的前驱节点了，因为 prev 指针直接就告诉我们了。
删除节点 p 的操作就像是告诉它的邻居们互相认识：
- 让
p的前一个节点的next指针，指向p的后一个节点。 - 让
p的后一个节点的prev指针，指向p的前一个节点。 - 安全地销毁
p。
这个删除过程是 O(1) 的！当然，代价是我们需要更多的内存来存储 prev 指针，并且在插入和删除时需要同时维护 next 和 prev 两个指针，逻辑更复杂一些。
循环链表
在循环链表（Circular Linked List）中，最后一个节点的 next 指针并非指向空指针 (nullptr)，而是回指到链表的首节点，从而使整个链表形成一个首尾相连的闭环结构。
这种“无尽循环”的特性在某些场景下非常有用，比如操作系统的时间片轮转调度。每个程序就像一个节点，系统轮流给每个程序一点运行时间，然后把它放到队尾，接着处理下一个，形成一个公平的循环。
数组 vs. 链表
现在，我们可以清晰地看到数组和链表这两种数据结构之间的根本差异和权衡。
- 当你需要频繁地、快速地通过索引访问数据时，就像查字典一样，数组是你的不二之选。它的 O(1) 随机访问能力无可替代。
- 当你的应用需要频繁地在列表的开头（或者中间，如果你能快速定位）进行插入和删除，而对随机访问要求不高时，链表则能大放异彩。
- 如果不确定，从
std::vector(C++的动态数组) 开始通常是明智的选择，因为它在大多数情况下都表现得足够好。
链表不仅仅是一种数据结构，它更是一种思想——用指针将逻辑上相关但物理上分散的数据串联起来。这种思想是构建许多更高级数据结构（如图、树）的基石。
小练习
- 在链表头部插入节点的时间复杂度是？
- 在链表尾部插入节点（无tail指针优化）的时间复杂度是？
- 在链表中查找指定值的节点的时间复杂度是？
4. 链表基本操作练习
实现一个简单的链表类，并完成以下操作：
- 在头部插入节点：依次插入
3,2,1 - 在尾部插入节点：依次插入
4,5 - 实现
PrintList()方法，遍历并打印所有节点的数据 - 删除值为
3的节点，并再次打印链表
#include <iostream>
using namespace std;
// 链表节点类
class Node
{
public:
int data;
Node* next;
Node(int data)
{
this->data = data;
this->next = nullptr;
}
};
// 链表类
class LinkedList
{
private:
Node* head;
public:
LinkedList()
{
head = nullptr;
}
// 在头部插入节点 - O(1)
void insertAtHead(int value)
{
Node* newNode = new Node(value);
newNode->next = head;
head = newNode;
}
// 在尾部插入节点 - O(n)
void insertAtTail(int value)
{
Node* newNode = new Node(value);
if (head == nullptr)
{
head = newNode;
return;
}
Node* current = head;
while (current->next != nullptr)
{
current = current->next;
}
current->next = newNode;
}
// 删除指定值的节点 - O(n)
bool deleteValue(int value)
{
if (head == nullptr) return false;
// 如果头节点就是要删除的节点
if (head->data == value)
{
Node* temp = head;
head = head->next;
delete temp;
return true;
}
// 查找要删除的节点
Node* prev = nullptr;
Node* current = head;
while (current != nullptr && current->data != value)
{
prev = current;
current = current->next;
}
// 如果找到了，删除它
if (current != nullptr)
{
prev->next = current->next;
delete current;
return true;
}
return false;
}
// 打印链表 - O(n)
void printList()
{
if (head == nullptr)
{
cout << "链表为空" << endl;
return;
}
Node* current = head;
while (current != nullptr)
{
cout << current->data;
if (current->next != nullptr)
{
cout << " -> ";
}
current = current->next;
}
cout << endl;
}
// 析构函数：释放内存
~LinkedList()
{
Node* current = head;
while (current != nullptr)
{
Node* temp = current;
current = current->next;
delete temp;
}
}
};
int main()
{
LinkedList list;
// 在头部插入 3, 2, 1
cout << "在头部插入 3, 2, 1:" << endl;
list.insertAtHead(3);
list.insertAtHead(2);
list.insertAtHead(1);
list.printList(); // 输出: 1 -> 2 -> 3
// 在尾部插入 4, 5
cout << "\n在尾部插入 4, 5:" << endl;
list.insertAtTail(4);
list.insertAtTail(5);
list.printList(); // 输出: 1 -> 2 -> 3 -> 4 -> 5
// 删除值为 3 的节点
cout << "\n删除值为 3 的节点:" << endl;
list.deleteValue(3);
list.printList(); // 输出: 1 -> 2 -> 4 -> 5
return 0;
}在头部插入 3, 2, 1:
1 -> 2 -> 3
在尾部插入 4, 5:
1 -> 2 -> 3 -> 4 -> 5
删除值为 3 的节点:
1 -> 2 -> 4 -> 5说明：
- InsertAtHead：时间复杂度 O(1)，只需要修改头指针
- InsertAtTail：时间复杂度 O(n)，需要遍历到尾部
- DeleteValue：时间复杂度 O(n)，需要查找目标节点
- PrintList：时间复杂度 O(n)，需要遍历所有节点
5. 链表反转练习
实现链表的反转方法 Reverse()，将整个链表反转。
- 例如：
1 -> 2 -> 3 -> 4反转后变成4 -> 3 -> 2 -> 1 - 要求：使用三个指针（
prev,current,next）来完成操作 - 提示：在遍历链表时，逐个节点地改变其
Next指针的方向
#include <iostream>
using namespace std;
class Node
{
public:
int data;
Node* next;
Node(int data)
{
this->data = data;
this->next = nullptr;
}
};
class LinkedList
{
private:
Node* head;
public:
LinkedList()
{
head = nullptr;
}
void insertAtHead(int value)
{
Node* newNode = new Node(value);
newNode->next = head;
head = newNode;
}
// 反转链表 - O(n)
void reverse()
{
Node* prev = nullptr; // 前一个节点，初始为空
Node* current = head; // 当前节点，从头开始
Node* next = nullptr; // 下一个节点
while (current != nullptr)
{
// 保存下一个节点，因为我们要改变 current->next
next = current->next;
// 反转：让当前节点指向前一个节点
current->next = prev;
// 移动指针：prev 和 current 都向前移动
prev = current;
current = next;
}
// 新的头是原来的尾（prev）
head = prev;
}
void printList()
{
if (head == nullptr)
{
cout << "链表为空" << endl;
return;
}
Node* current = head;
while (current != nullptr)
{
cout << current->data;
if (current->next != nullptr)
{
cout << " -> ";
}
current = current->next;
}
cout << endl;
}
// 析构函数：释放内存
~LinkedList()
{
Node* current = head;
while (current != nullptr)
{
Node* temp = current;
current = current->next;
delete temp;
}
}
};
int main()
{
LinkedList list;
// 创建链表 1 -> 2 -> 3 -> 4
list.insertAtHead(4);
list.insertAtHead(3);
list.insertAtHead(2);
list.insertAtHead(1);
cout << "反转前:" << endl;
list.printList(); // 输出: 1 -> 2 -> 3 -> 4
list.reverse();
cout << "反转后:" << endl;
list.printList(); // 输出: 4 -> 3 -> 2 -> 1
return 0;
}反转前:
1 -> 2 -> 3 -> 4
反转后:
4 -> 3 -> 2 -> 1说明：
- 时间复杂度：O(n)，需要遍历链表一次
- 空间复杂度：O(1)，只使用了三个指针变量
- 核心思想：
- 使用三个指针：
prev（前一个）、current（当前）、next（下一个） - 在遍历过程中，将每个节点的
Next指针指向前一个节点 - 最后，原来的尾节点成为新的头节点
- 使用三个指针：
- 关键步骤：
- 保存
next = current.Next（避免丢失下一个节点） - 反转
current.Next = prev（改变指针方向） - 移动指针
prev = current; current = next（继续遍历）
- 保存
6. 寻找中间节点练习
实现一个方法 FindMiddle()，找出链表的中间节点。
- 如果链表有奇数个节点，返回中间节点
- 如果链表有偶数个节点，返回第二个中间节点
- 例如：
1 -> 2 -> 3 -> 4 -> 5的中间节点是3 - 例如：
1 -> 2 -> 3 -> 4的中间节点是3 - 要求：使用快慢指针技巧（快指针每次走两步，慢指针每次走一步）
#include <iostream>
using namespace std;
class Node
{
public:
int data;
Node* next;
Node(int data)
{
this->data = data;
this->next = nullptr;
}
};
class LinkedList
{
private:
Node* head;
public:
LinkedList()
{
head = nullptr;
}
void insertAtHead(int value)
{
Node* newNode = new Node(value);
newNode->next = head;
head = newNode;
}
// 寻找中间节点 - O(n)
Node* findMiddle()
{
if (head == nullptr) return nullptr;
// 快慢指针技巧
Node* slow = head; // 慢指针，每次走一步
Node* fast = head; // 快指针，每次走两步
// 当快指针到达末尾时，慢指针就在中间
while (fast != nullptr && fast->next != nullptr)
{
slow = slow->next; // 慢指针走一步
fast = fast->next->next; // 快指针走两步
}
return slow;
}
void printList()
{
if (head == nullptr)
{
cout << "链表为空" << endl;
return;
}
Node* current = head;
while (current != nullptr)
{
cout << current->data;
if (current->next != nullptr)
{
cout << " -> ";
}
current = current->next;
}
cout << endl;
}
// 析构函数：释放内存
~LinkedList()
{
Node* current = head;
while (current != nullptr)
{
Node* temp = current;
current = current->next;
delete temp;
}
}
};
int main()
{
// 测试奇数个节点
LinkedList list1;
list1.insertAtHead(5);
list1.insertAtHead(4);
list1.insertAtHead(3);
list1.insertAtHead(2);
list1.insertAtHead(1);
cout << "链表1（奇数个节点）:" << endl;
list1.printList(); // 输出: 1 -> 2 -> 3 -> 4 -> 5
Node* middle1 = list1.findMiddle();
if (middle1 != nullptr)
{
cout << "中间节点: " << middle1->data << endl; // 输出: 3
}
// 测试偶数个节点
LinkedList list2;
list2.insertAtHead(4);
list2.insertAtHead(3);
list2.insertAtHead(2);
list2.insertAtHead(1);
cout << "\n链表2（偶数个节点）:" << endl;
list2.printList(); // 输出: 1 -> 2 -> 3 -> 4
Node* middle2 = list2.findMiddle();
if (middle2 != nullptr)
{
cout << "中间节点: " << middle2->data << endl; // 输出: 3（第二个中间节点）
}
return 0;
}链表1（奇数个节点）:
1 -> 2 -> 3 -> 4 -> 5
中间节点: 3
链表2（偶数个节点）:
1 -> 2 -> 3 -> 4
中间节点: 3说明：
- 时间复杂度：O(n)，只需要遍历链表一次
- 空间复杂度：O(1)，只使用了两个指针变量
- 快慢指针技巧：
- 慢指针
slow每次走一步 - 快指针
fast每次走两步 - 当快指针到达末尾时，慢指针就在中间位置
- 慢指针
- 为什么这样能工作：
- 如果链表有 n 个节点，快指针需要走 n 步到达末尾
- 慢指针同时走了 n/2 步，正好在中间位置
- 对于偶数个节点，慢指针会停在第二个中间节点（因为
fast.Next != null的条件）