栈 | 自在学栈
在数据结构的学习中,我们已经掌握了数组和链表等线性结构,它们支持在任意位置进行插入和删除操作。现在,我们将探讨一种具有特定约束的线性数据结构——栈(Stack)。这种约束性并非缺陷,而是栈的核心特征,使其在特定场景下展现出卓越的性能和简洁性。
栈是一种遵循后进先出(Last-In, First-Out, LIFO)原则的抽象数据类型。在栈中,元素的插入和删除操作都只能在同一个端点进行,这个端点称为栈顶(Top)。与栈顶相对的另一端称为栈底(Bottom)。栈的这种特性可以形式化地定义为:对于任意元素序列,最后插入的元素将最先被移除。
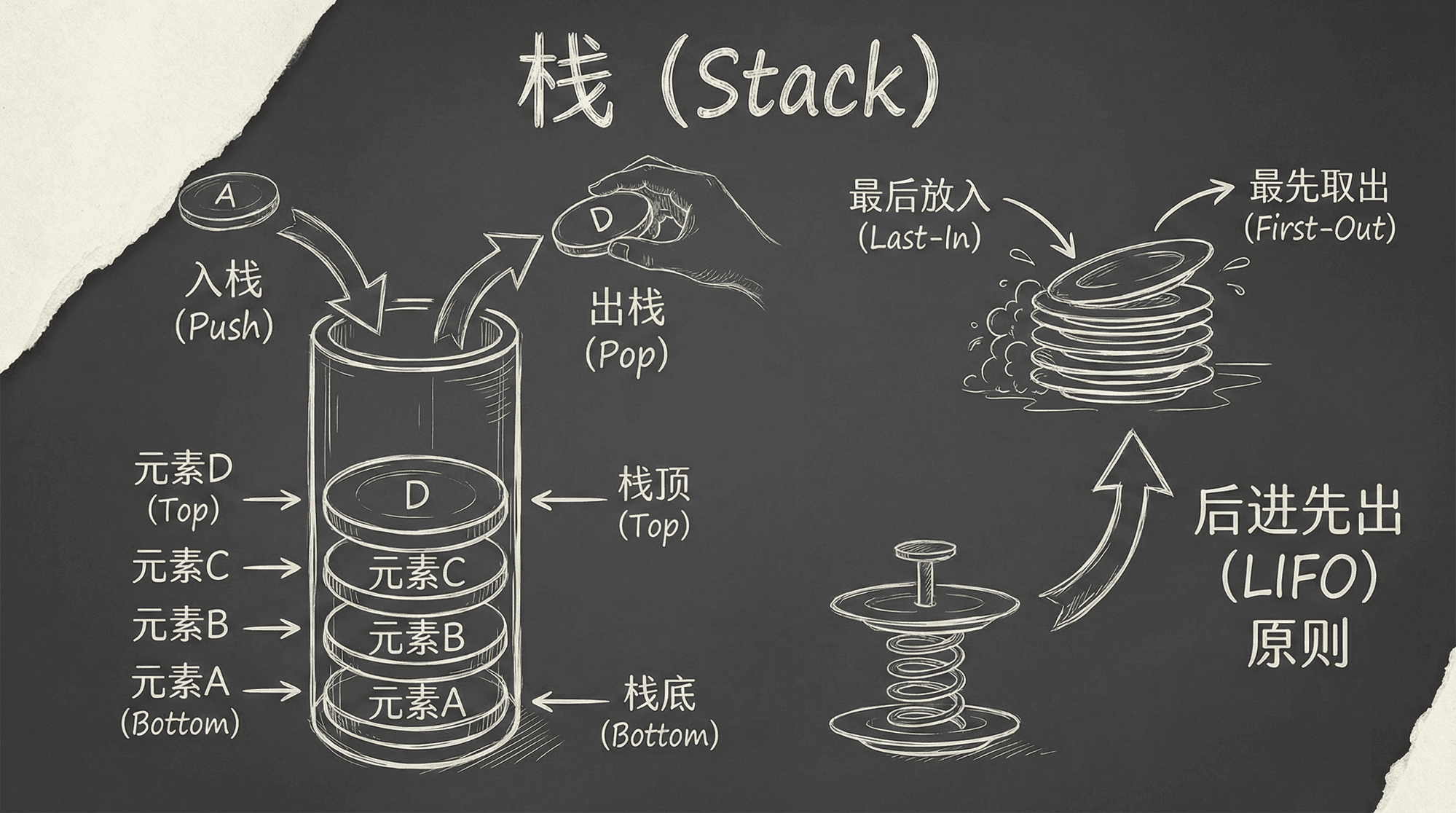
从形式化角度来看,栈可以定义为一个有序对 (S, op),其中 S 是元素的集合,op 是定义在 S 上的操作集合。栈的核心约束在于:所有修改操作(插入和删除)都必须在栈顶执行,这确保了元素访问顺序的严格性。这种设计使得栈在函数调用管理、表达式求值、回溯算法等场景中具有不可替代的作用。
栈的基本操作
栈作为抽象数据类型,定义了以下基本操作接口。每个操作都有明确的前置条件和后置条件,以及确定的时间复杂度。
- 推入(Push):操作将一个元素添加到栈顶。该操作的前置条件是栈已初始化,后置条件是栈的大小增加1,新元素成为栈顶元素。推入操作的时间复杂度为 O(1)。
- 弹出(Pop):操作移除并返回栈顶元素。该操作的前置条件是栈非空,后置条件是栈的大小减少1,原栈顶的下一个元素成为新的栈顶。如果对空栈执行弹出操作,将引发下溢(Underflow)异常。弹出操作的时间复杂度为 O(1)。
- 查看栈顶(Top 或 Peek):操作返回栈顶元素的值,但不移除该元素。该操作的前置条件是栈非空,后置条件是栈的状态不变。查看操作的时间复杂度为 O(1)。
- 判空(isEmpty):操作检查栈是否为空,返回布尔值。该操作的时间复杂度为 O(1)。
- 获取大小(Size):操作返回栈中当前元素的数量。该操作的时间复杂度为 O(1),具体实现取决于底层数据结构的选择。
下面的流程图展示了栈操作的基本执行序列,栈顶元素用 C 表示:
这些基本操作构成了栈的完整接口。虽然操作集合简单,但通过它们的组合可以解决许多复杂的计算问题。
栈实验室
栈的实现
栈作为抽象数据类型,可以通过多种底层数据结构实现。不同的实现方式在时间复杂度、空间复杂度、缓存性能等方面存在差异。下面我们探讨两种主要的实现方式。
基于动态数组的栈
使用动态数组(在C++中为 std::vector)实现栈是最常见且高效的方式。在这种实现中,我们将数组的末尾作为栈顶,利用数组的连续内存布局和高效的尾部操作。
- 内存布局特性:动态数组在内存中连续存储元素,这种布局具有优秀的空间局部性(Spatial Locality)。当CPU访问栈顶元素时,相邻元素很可能已经被加载到缓存中,从而显著提升访问速度。每个元素的内存地址可以通过基址加上索引偏移量直接计算得出,访问时间为 O(1)。
- 扩容机制与摊销分析:当数组容量不足时,
std::vector 会执行扩容操作。典型的扩容策略是分配原容量两倍的新空间,然后将所有元素复制到新空间。虽然单次扩容的时间复杂度为 O(n),但通过摊销分析(Amortized Analysis)可以证明,n 次推入操作的总时间复杂度为 O(n),因此单次推入操作的摊销时间复杂度为 O(1)。
- 时间复杂度分析:基于动态数组的栈实现中,所有基本操作的时间复杂度如下:推入操作在最坏情况下为 O(n)(需要扩容),摊销时间复杂度为 O(1);弹出操作为 O(1);查看栈顶为 O(1);判空和获取大小均为 O(1)。
让我们来看一个具体的C++实现:
#include <vector>
#include <stdexcept>
template <typename T>
class VectorStack {
private:
// 使用 std::vector 作为底层容器
// vector 的末尾索引对应栈顶位置
// 这种设计充分利用了连续内存的缓存优势
std::vector<T> elements;
public:
// 推入操作:将元素添加到栈顶
// 时间复杂度:摊销 O(1),最坏情况 O(n)(扩容时)
void push(const T& item) {
// vector::push_back 在末尾添加元素
// 利用连续内存布局,访问效率高
基于链表的栈
链表实现栈的方式是将链表的头部作为栈顶。每次推入操作在链表头部插入新节点,弹出操作删除头部节点。这种实现方式的所有操作都保证在严格的 O(1) 时间内完成,不存在性能波动。
- 内存分配特性:链表节点通过动态内存分配创建,每个节点在堆内存中独立存在。节点之间通过指针连接,内存布局是非连续的。每个节点除了存储数据外,还需要额外的指针空间(在64位系统上通常为8字节)。
- 内存开销分析:假设存储类型 T 的大小为 sizeof(T),每个节点需要 sizeof(T) + sizeof(Node*) 的内存空间。对于小数据类型(如 int),指针开销可能占比较大比例。此外,动态分配可能导致内存碎片化,降低内存利用率。
- 缓存性能:由于节点在内存中非连续分布,访问模式缺乏空间局部性。当访问栈顶节点时,下一个节点很可能不在同一缓存行中,需要额外的内存访问。这种跳跃式访问模式对CPU缓存不友好,实际运行速度通常低于数组实现。
#include <stdexcept>
// 链表节点结构体
template <typename T>
struct Node {
T data; // 节点存储的数据
Node* next; // 指向下一个节点的指针
// 构造函数:初始化节点数据,next 指针设为 nullptr
Node(const T& data) : data(data), next(nullptr) {}
};
template <typename T>
实现方式对比与选择
两种实现方式在多个维度上存在显著差异,选择时需要根据具体应用场景进行权衡。
- 时间复杂度对比:基于动态数组的实现中,推入操作的摊销时间复杂度为 O(1),但在扩容时会出现 O(n) 的峰值。基于链表的实现中,所有操作都严格保证 O(1) 时间复杂度,不存在性能波动。
- 空间复杂度分析:动态数组实现的空间复杂度为 O(n),其中 n 为元素数量。由于扩容策略,实际分配的空间可能略大于 n,但空间利用率通常较高。链表实现的空间复杂度也为 O(n),但每个节点需要额外的指针开销,且可能存在内存碎片,实际空间利用率较低。
- 缓存性能差异:动态数组的连续内存布局具有优秀的缓存局部性。当访问栈顶元素时,相邻元素很可能在同一缓存行中,减少了缓存未命中的概率。链表的非连续内存布局导致缓存性能较差,每次访问都可能触发缓存未命中,需要从主内存加载数据。
- 适用场景:对于大多数应用场景,基于动态数组的实现是首选。它在平均情况下具有更好的性能,且实现简单。C++ 标准库中的
std::stack 默认使用 std::deque 作为底层容器,这是一种结合了数组和链表优点的数据结构。只有在需要严格保证每次操作都是 O(1) 且对性能波动极其敏感的场景(如实时系统、嵌入式系统)中,才考虑使用链表实现。
- 标准库使用:在实际开发中,推荐直接使用 C++ 标准库提供的
std::stack,它已经过充分优化和测试。std::stack 是一个容器适配器,默认使用 std::deque 作为底层容器,也可以指定使用 std::vector 或 std::list。
#include <stack>
#include <vector>
// 使用默认底层容器(std::deque)
std::stack<int> defaultStack;
// 指定使用 std::vector 作为底层容器
std::stack<int, std::vector<int>> vectorStack;
// 基本操作示例
vectorStack.push(10);
vectorStack.push(20);
int topValue = vectorStack.top(); // 20
vectorStack.
栈的应用
栈的 LIFO 特性使其在计算机科学的多个领域具有重要应用。下面我们探讨几个典型的应用场景。
函数调用与调用栈
在程序执行过程中,函数调用和返回的管理依赖于调用栈(Call Stack) 机制。调用栈是栈数据结构在运行时系统中的应用,用于维护函数调用的执行上下文。
栈帧(Stack Frame) 是调用栈中的基本单元,也称为活动记录(Activation Record)。每个栈帧包含以下信息:局部变量、函数参数、返回地址、调用者的栈帧指针、以及可能的临时计算结果。当函数被调用时,系统为其创建一个新的栈帧并推入调用栈;当函数返回时,对应的栈帧被弹出,控制权返回到调用者。
调用序列示例:假设 main 函数调用 functionA,functionA 又调用 functionB。调用栈的状态变化如下:首先 main 的栈帧被推入;然后 functionA 的栈帧被推入,位于 main 之上;接着 functionB 的栈帧被推入,位于栈顶。当 functionB 执行完毕返回时,其栈帧被弹出,控制权回到 functionA;functionA 返回时,其栈帧被弹出,控制权回到 main。
栈溢出(Stack Overflow):调用栈的大小是有限的,通常由操作系统或编译器设置。当递归深度过大或局部变量占用空间过多时,可能耗尽栈空间,导致栈溢出错误。这是无限递归或深度递归算法中常见的问题。
后缀表达式求值
后缀表达式(Postfix Notation),也称为逆波兰表示法(Reverse Polish Notation),是一种不需要括号的数学表达式表示方法。在后缀表达式中,运算符位于其操作数之后。例如,中缀表达式 (3 + 4) * 5 对应的后缀表达式为 3 4 + 5 *。
算法描述:后缀表达式求值算法使用栈作为辅助数据结构。算法从左到右扫描表达式,遇到操作数时将其推入栈,遇到运算符时从栈中弹出所需数量的操作数,执行运算后将结果推入栈。算法的时间复杂度为 O(n),其中 n 为表达式长度,空间复杂度为 O(n)。
执行过程示例:对于后缀表达式 3 4 + 5 *,执行过程如下:扫描到 3,推入栈,栈状态为 [3];扫描到 4,推入栈,栈状态为 [3, 4];扫描到 +,弹出 4 和 3,计算 3 + 4 = 7,将 7 推入栈,栈状态为 [7];扫描到 5,推入栈,栈状态为 [7, 5];扫描到 *,弹出 5 和 7,计算 7 * 5 = 35,将 35 推入栈,栈状态为 [35]。表达式扫描完毕,栈顶元素 35 即为最终结果。
中缀转后缀算法:将中缀表达式转换为后缀表达式同样可以使用栈实现。算法维护一个运算符栈,根据运算符优先级和结合性规则处理运算符。该算法的时间复杂度为 O(n),空间复杂度为 O(n)。
括号匹配
括号匹配是栈的经典应用之一。给定一个包含多种括号(圆括号、方括号、花括号)的字符串,判断其中的括号是否匹配。算法使用栈存储未匹配的左括号,遇到右括号时检查栈顶是否是对应的左括号。算法的时间复杂度和空间复杂度均为 O(n),其中 n 为字符串长度。
深度优先搜索
在图的遍历算法中,深度优先搜索(Depth-First Search, DFS) 可以使用栈来实现。算法从起始顶点开始,将未访问的相邻顶点推入栈,然后从栈中弹出顶点进行访问,重复此过程直到栈为空。使用栈实现的 DFS 与递归实现等价,但提供了更明确的控制流程。
复杂度分析总结
下表总结了基于不同底层数据结构的栈操作的时间复杂度:
空间复杂度方面,两种实现均为 O(n),其中 n 为栈中元素数量。动态数组实现的空间利用率通常更高,而链表实现存在指针开销和内存碎片问题。
小练习
- 如果只使用一个普通栈,getMin()操作的时间复杂度是?
4. 栈操作序列追踪练习
给定一个初始状态为空的栈,执行以下操作序列:push(10), push(20), top(), push(30), pop(), pop(), push(40), isEmpty(), pop(), pop(), isEmpty(), pop()。
请完整追踪整个操作序列的执行过程,并回答:
- 每次调用
top() 操作时,返回的元素值是什么?
- 每次执行
pop() 操作后,栈的内部状态如何变化?
- 每次调用
isEmpty() 操作时,返回值是 true 还是 false?
- 最后一次
pop() 操作会产生什么结果?
#include <iostream>
#include <stack>
#include <vector>
#include <sstream>
#include <algorithm>
using namespace std;
// 辅助函数:打印栈的内容(从栈顶到栈底)
string stackToString(stack<int> s)
{
if (s.empty()) return "[]";
vector<int> vec;
while
5. 最小栈数据结构设计练习
设计并实现一个扩展的栈数据结构,在支持标准栈操作(push(x)、pop()、top())的基础上,额外提供 getMin() 操作,该操作需要在 O(1) 时间复杂度内返回栈中的最小元素。
要求:所有操作(push、pop、top、getMin)的时间复杂度均为 O(1)。
#include <iostream>
#include <stack>
#include <stdexcept>
using namespace std;
class MinStack
{
private:
// 主栈:存储所有元素
stack<int> mainStack;
// 辅助栈:存储每个状态下的最小值
// 辅助栈的栈顶元素始终等于主栈当前状态下的最小值
stack<int> minStack;
public:
MinStack()
{
// 栈会自动初始化
}
// 入栈操作 - O(1)
void push
6. 每日温度问题练习
给定一个整数数组 temperatures,其中 temperatures[i] 表示第 i 天的温度值。对于数组中的每个元素,计算需要等待多少天才能遇到一个更高的温度值。如果之后没有更高的温度,则结果为 0。
要求:返回一个整数数组 result,其中 result[i] 表示第 i 天需要等待的天数。使用单调栈方法解决,时间复杂度为 O(n)。
#include <iostream>
#include <vector>
#include <stack>
#include <sstream>
using namespace std;
// 辅助函数:打印数组
string arrayToString(const vector<int>& arr)
{
if (arr.empty()) return "[]";
stringstream ss;
ss << "[";
for
elements.push_back(item);
}
// 弹出操作:移除并返回栈顶元素
// 时间复杂度:O(1)
void pop() {
// 前置条件检查:防止对空栈执行弹出操作
if (isEmpty()) {
throw std::out_of_range("栈下溢:无法从空栈中弹出元素");
}
// vector::pop_back 移除最后一个元素,时间复杂度为 O(1)
elements.pop_back();
}
// 查看栈顶元素:返回栈顶元素的引用,不修改栈状态
// 时间复杂度:O(1)
T& top() {
// 前置条件检查:确保栈非空
if (isEmpty()) {
throw std::out_of_range("无法访问空栈的栈顶元素");
}
// vector::back 返回最后一个元素的引用
// 由于是连续内存,直接通过索引访问,时间复杂度 O(1)
return elements.back();
}
// 常量版本的 top 操作,用于 const 对象
const T& top() const {
if (isEmpty()) {
throw std::out_of_range("无法访问空栈的栈顶元素");
}
return elements.back();
}
// 判空操作:检查栈是否为空
// 时间复杂度:O(1)
bool isEmpty() const {
return elements.empty();
}
// 获取栈的大小:返回当前元素数量
// 时间复杂度:O(1)
size_t size() const {
return elements.size();
}
};
class LinkedListStack {
private:
// 指向链表头部的指针,头部节点对应栈顶
Node<T>* head;
// 元素计数器,用于 O(1) 时间获取栈大小
size_t count;
public:
// 构造函数:初始化空栈
LinkedListStack() : head(nullptr), count(0) {}
// 析构函数:释放所有动态分配的内存
// 时间复杂度:O(n),n 为栈中元素数量
~LinkedListStack() {
// 依次弹出所有元素,释放每个节点的内存
while (!isEmpty()) {
pop();
}
}
// 拷贝构造函数和赋值运算符应被实现以避免浅拷贝问题
// 这里省略以保持代码简洁
// 推入操作:在链表头部插入新节点
// 时间复杂度:O(1)
void push(const T& data) {
// 1. 在堆内存中分配新节点
Node<T>* newNode = new Node<T>(data);
// 2. 将新节点的 next 指针指向当前头部
newNode->next = head;
// 3. 更新头部指针,新节点成为栈顶
head = newNode;
// 4. 更新元素计数
count++;
}
// 弹出操作:删除链表头部节点
// 时间复杂度:O(1)
void pop() {
// 前置条件检查
if (isEmpty()) {
throw std::out_of_range("栈下溢:无法从空栈中弹出元素");
}
// 1. 保存当前头部指针,用于后续内存释放
Node<T>* temp = head;
// 2. 将头部指针移动到下一个节点
head = head->next;
// 3. 释放原头部节点的内存
delete temp;
// 4. 更新元素计数
count--;
}
// 查看栈顶元素
// 时间复杂度:O(1)
T& top() {
if (isEmpty()) {
throw std::out_of_range("无法访问空栈的栈顶元素");
}
// 返回头部节点存储的数据
return head->data;
}
const T& top() const {
if (isEmpty()) {
throw std::out_of_range("无法访问空栈的栈顶元素");
}
return head->data;
}
// 判空操作
// 时间复杂度:O(1)
bool isEmpty() const {
// 头部指针为 nullptr 表示链表为空
return head == nullptr;
}
// 获取栈的大小
// 时间复杂度:O(1)
size_t size() const {
return count;
}
};
pop
();
(
!
s.
empty
())
{
vec.push_back(s.top());
s.pop();
}
// 反转,因为栈是后进先出,打印时应该从栈顶到栈底
reverse(vec.begin(), vec.end());
stringstream ss;
ss << "[";
for (size_t i = 0; i < vec.size(); i++)
{
ss << vec[i];
if (i < vec.size() - 1) ss << ", ";
}
ss << "]";
return ss.str();
}
int main()
{
stack<int> stk;
cout << "操作序列追踪:" << endl;
cout << "初始状态: 空栈" << endl;
cout << endl;
// push(10)
stk.push(10);
cout << "push(10) 后: " << stackToString(stk) << endl;
// push(20)
stk.push(20);
cout << "push(20) 后: " << stackToString(stk) << endl;
// top()
cout << "top() 返回: " << stk.top() << endl;
// push(30)
stk.push(30);
cout << "push(30) 后: " << stackToString(stk) << endl;
// pop()
int popped1 = stk.top();
stk.pop();
cout << "pop() 返回: " << popped1 << ", 栈状态: " << stackToString(stk) << endl;
// pop()
int popped2 = stk.top();
stk.pop();
cout << "pop() 返回: " << popped2 << ", 栈状态: " << stackToString(stk) << endl;
// push(40)
stk.push(40);
cout << "push(40) 后: " << stackToString(stk) << endl;
// isEmpty()
cout << "isEmpty() 返回: " << (stk.empty() ? "true" : "false") << endl;
// pop()
int popped3 = stk.top();
stk.pop();
cout << "pop() 返回: " << popped3 << ", 栈状态: " << stackToString(stk) << endl;
// pop()
int popped4 = stk.top();
stk.pop();
cout << "pop() 返回: " << popped4 << ", 栈状态: " << stackToString(stk) << endl;
// isEmpty()
cout << "isEmpty() 返回: " << (stk.empty() ? "true" : "false") << endl;
// pop() - 最后一次,会抛出异常
if (stk.empty())
{
cout << "pop() 抛出异常: 栈为空" << endl;
}
else
{
int popped5 = stk.top();
stk.pop();
cout << "pop() 返回: " << popped5 << endl;
}
return 0;
}
操作序列追踪:
初始状态: 空栈
push(10) 后: [10]
push(20) 后: [20, 10]
top() 返回: 20
push(30) 后: [30, 20, 10]
pop() 返回: 30, 栈状态: [20, 10]
pop() 返回: 20, 栈状态: [10]
push(40) 后: [40, 10]
isEmpty() 返回: False
pop() 返回: 40, 栈状态: [10]
pop() 返回: 10, 栈状态: []
isEmpty() 返回: True
pop() 抛出异常: Stack empty.
- top() 操作:返回栈顶元素
20,不改变栈的状态
- pop() 操作:依次弹出
30, 20, 40, 10,每次弹出后栈的状态都会改变
- isEmpty() 操作:
- 第一次调用时栈中有元素,返回
False
- 第二次调用时栈为空,返回
True
- 最后一次 pop():当栈为空时执行
pop() 会抛出 InvalidOperationException 异常
- 栈的 LIFO 特性:最后入栈的元素(
30)最先出栈,体现了后进先出的特性
(
int
x
)
{
// 将元素推入主栈
mainStack.push(x);
// 如果辅助栈为空,或新元素小于等于当前最小值,更新辅助栈
if (minStack.empty() || x <= minStack.top())
{
minStack.push(x);
}
}
// 出栈操作 - O(1)
void pop()
{
if (mainStack.empty())
{
throw runtime_error("栈为空,无法弹出元素");
}
// 如果主栈栈顶等于辅助栈栈顶(即当前最小值),同时弹出辅助栈
if (mainStack.top() == minStack.top())
{
minStack.pop();
}
// 弹出主栈栈顶
mainStack.pop();
}
// 获取栈顶元素 - O(1)
int top()
{
if (mainStack.empty())
{
throw runtime_error("栈为空,无法访问栈顶元素");
}
return mainStack.top();
}
// 获取最小值 - O(1)
int getMin()
{
if (minStack.empty())
{
throw runtime_error("栈为空,无法获取最小值");
}
// O(1) 时间返回最小值
return minStack.top();
}
};
int main()
{
MinStack minStack;
minStack.push(5);
cout << "push(5) 后,最小值: " << minStack.getMin() << endl; // 5
minStack.push(3);
cout << "push(3) 后,最小值: " << minStack.getMin() << endl; // 3
minStack.push(7);
cout << "push(7) 后,最小值: " << minStack.getMin() << endl; // 3
minStack.push(2);
cout << "push(2) 后,最小值: " << minStack.getMin() << endl; // 2
minStack.pop(); // 弹出 2
cout << "pop() 后,最小值: " << minStack.getMin() << endl; // 3
minStack.pop(); // 弹出 7
cout << "pop() 后,最小值: " << minStack.getMin() << endl; // 3
cout << "当前栈顶: " << minStack.top() << endl; // 3
return 0;
}
push(5) 后,最小值: 5
push(3) 后,最小值: 3
push(7) 后,最小值: 3
push(2) 后,最小值: 2
pop() 后,最小值: 3
pop() 后,最小值: 3
当前栈顶: 3
- 设计思路:使用辅助栈存储每个状态下的最小值
- Push 操作:
- 将元素推入主栈
- 如果辅助栈为空或新元素 ≤ 辅助栈栈顶,将新元素也推入辅助栈
- Pop 操作:
- 如果主栈栈顶等于辅助栈栈顶(即当前最小值),同时弹出辅助栈
- 弹出主栈栈顶
- GetMin 操作:直接返回辅助栈栈顶,时间复杂度 O(1)
- 时间复杂度:所有操作均为 O(1)
- 空间复杂度:O(n),辅助栈在最坏情况下需要存储 n 个元素
(
size_t
i
=
0
; i
<
arr.
size
(); i
++
)
{
ss << arr[i];
if (i < arr.size() - 1) ss << ", ";
}
ss << "]";
return ss.str();
}
// 每日温度问题 - 使用单调栈
vector<int> dailyTemperatures(const vector<int>& temperatures)
{
int n = temperatures.size();
vector<int> result(n, 0);
stack<int> stk; // 存储索引,栈中索引对应的温度值单调递减
for (int i = 0; i < n; i++)
{
// 当栈非空且当前温度大于栈顶索引对应的温度时
while (!stk.empty() && temperatures[i] > temperatures[stk.top()])
{
int prevIndex = stk.top();
stk.pop();
// 计算等待天数
result[prevIndex] = i - prevIndex;
}
// 将当前索引推入栈
stk.push(i);
}
// 栈中剩余的索引对应的结果值保持为 0(表示之后没有更高的温度)
return result;
}
int main()
{
vector<int> temperatures = { 23, 24, 25, 21, 19, 22, 26, 23 };
vector<int> result = dailyTemperatures(temperatures);
cout << "温度数组:" << endl;
cout << arrayToString(temperatures) << endl;
cout << "\n等待天数:" << endl;
cout << arrayToString(result) << endl;
cout << "\n详细分析:" << endl;
for (size_t i = 0; i < temperatures.size(); i++)
{
if (result[i] > 0)
{
cout << "第 " << i << " 天温度 " << temperatures[i]
<< "°C,等待 " << result[i] << " 天后遇到更高温度 "
<< temperatures[i + result[i]] << "°C" << endl;
}
else
{
cout << "第 " << i << " 天温度 " << temperatures[i]
<< "°C,之后没有更高温度" << endl;
}
}
return 0;
}
温度数组:
[23, 24, 25, 21, 19, 22, 26, 23]
等待天数:
[1, 1, 4, 2, 1, 1, 0, 0]
详细分析:
第 0 天温度 23°C,等待 1 天后遇到更高温度 24°C
第 1 天温度 24°C,等待 1 天后遇到更高温度 25°C
第 2 天温度 25°C,等待 4 天后遇到更高温度 26°C
第 3 天温度 21°C,等待 2 天后遇到更高温度 22°C
第 4 天温度 19°C,等待 1 天后遇到更高温度 22°C
第 5 天温度 22°C,等待 1 天后遇到更高温度 26°C
第 6 天温度 26°C,之后没有更高温度
第 7 天温度 23°C,之后没有更高温度
- 单调栈方法:使用单调递减栈存储索引,栈中索引对应的温度值保持单调递减
- 算法步骤:
- 初始化结果数组,所有元素设为 0
- 从左到右遍历温度数组
- 当栈非空且当前温度大于栈顶索引对应的温度时:
- 弹出栈顶索引
j
- 计算
result[j] = i - j
- 将当前索引推入栈
- 时间复杂度:O(n),每个索引最多被推入和弹出栈各一次
- 空间复杂度:O(n),最坏情况下所有索引都在栈中
- 关键思想:单调栈保证了当我们处理索引
i 时,栈中存储的是所有尚未找到下一个更高温度的索引
