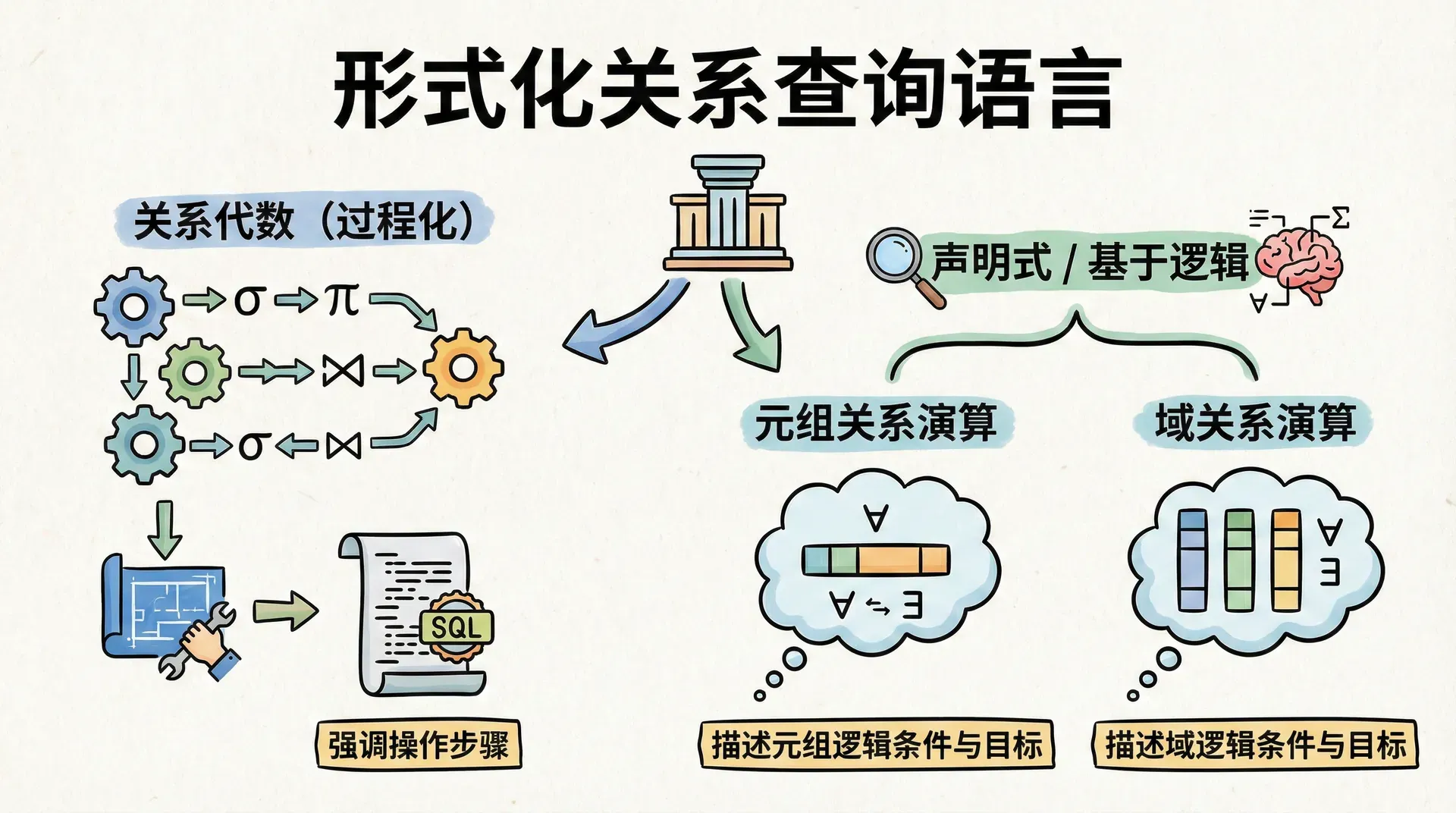
形式化关系查询语言

在前面的内容中，我们已经系统学习了关系模型及其对应的 SQL 查询语言。为了更深入地理解这些实际技术的理论基础，有必要掌握形式化关系查询语言。形式化查询语言为数据库查询操作提供了严谨的数学描述和分析框架，是数据库理论的核心组成部分。

所以我们将系统介绍三类主要的形式化查询语言：关系代数、元组关系演算和域关系演算。关系代数是 SQL 的理论基础，采用过程化范式，强调查询的操作步骤；元组关系演算和域关系演算则基于一阶逻辑，采用声明式范式，侧重于描述查询的逻辑条件和目标结果。

关系代数

关系代数是一种过程化的关系查询语言，具有严密的数学基础。它通过定义一组基本操作，对关系（即关系数据库中的表）进行处理，每个操作以一个或两个关系作为输入，输出一个新的关系，从而实现对数据的查询与变换。

在理论上，关系可以被视为数学意义上的集合，关系代数则规定了在这些集合上可执行的各种运算规则。通过组合这些操作，可以构建出复杂的查询表达式，以满足多样化的数据检索需求。

关系代数包括六种基本操作：选择（Selection）、投影（Projection）、并集（Union）、差集（Set Difference）、笛卡尔积（Cartesian Product）和重命名（Rename）。此外，还存在若干衍生操作，如交集（Intersection）、自然连接（Natural Join）和赋值（Assignment）等，这些衍生操作均可通过基本操作进行定义和实现。

基础操作

关系代数的基本操作可分为两大类：一元操作和二元操作。其中，选择（Selection）、投影（Projection）和重命名（Rename）属于一元操作，仅作用于单一关系；并集（Union）、差集（Set Difference）和笛卡尔积（Cartesian Product）属于二元操作，需以两个关系为输入对象。

选择操作

选择操作（Selection）用于从关系中选取满足给定谓词条件的元组。该操作以希腊字母σ（sigma）表示，选择条件作为下标，操作对象的关系作为括号内的参数。

例如，考虑一个教师关系，记录了教师的基本信息：

|
-- 教师表示例数据
教师ID | 姓名   | 系别     | 薪资
10001  | 张教授  | 计算机系  | 85000
10002  | 李老师  | 数学系    | 75000  
10003  | 王教授  | 物理系    | 95000
10004  | 陈老师  | 计算机系  | 88000
10005  | 赵教授  | 化学系    | 72000

如果我们要查找计算机系的所有教师，用关系代数表示就是：

这个操作的结果会是：

选择操作支持各种比较运算符，包括等于=、不等于≠、小于<、小于等于≤、大于>和大于等于≥。我们还可以用逻辑连接词将多个条件组合起来，包括"与"∧、"或"∨和"非"¬。

比如，如果我们想找出计算机系中薪资超过80000的教师，可以写成：

选择条件还可以比较同一记录中的不同属性。例如，在一个部门表中，如果我们要找出部门名称与大楼名称相同的部门：

投影操作

投影操作帮我们从关系中选择需要的列，就像从一张表格中只保留我们关心的几列信息。我们用希腊字母π（pi）来表示投影操作，需要保留的属性作为下标列出。

继续用教师表来举例。假设我们只关心教师的姓名和薪资信息，不需要教师ID和系别，可以写成：

结果会是：

投影操作有一个重要特性：由于关系本质上是集合，任何重复的记录都会被自动消除。假设我们只投影系别信息：

得到的结果是：

需要注意的是，由于关系模型中关系本质上是集合，投影操作会自动去除重复元组。例如，尽管原始教师表中存在多位属于“计算机系”的教师，投影结果中“计算机系”仅出现一次。

关系代数表达式的组合

关系代数的一个核心特性是操作的封闭性：任意关系代数操作的输出依然是关系，因此可以作为后续操作的输入。这一特性使得我们能够通过嵌套和组合基本操作，构造出复杂的查询表达式。

例如，若需查询“物理系所有教师的姓名”，可将选择（σ）与投影（π）操作进行组合：

这个表达式先用选择操作筛选出物理系的教师，然后用投影操作只保留姓名信息。就像数学表达式一样，关系代数表达式也可以通过组合基本操作来表达复杂的查询需求。

并集操作

并集（Union）操作用于将两个关系中的所有元组合并为一个新的关系，结果中自动去除重复元组。并集在关系代数中用符号 ∪ 表示，其语义与数学中集合的并集一致。

例如，设有两个学期的课程安排，现需查询“2023年秋季学期或2024年春季学期开设的所有课程”。假定课程表包含属性：课程ID、学期、年份。

要获取这两个学期开设的所有课程，我们可以写成：

结果是：

注意CS-101在两个学期都有开设，但在结果中只出现一次，这体现了集合的特性。

差集操作

差集操作（Set Difference）是关系代数中的基本集合运算之一，用于从一个关系中剔除出现在另一个关系中的所有元组。其符号为 −，语义为“属于第一个关系但不属于第二个关系的所有元组”。差集常用于实现诸如“查询A中存在但B中不存在的数据”等需求。

以课程表为例，若需查询“2023年秋季学期开设但2024年春季学期未开设的所有课程”，可通过差集操作实现：

结果是：

差集操作同样要求两个关系必须兼容，即属性数量相同且对应属性的域相同。

笛卡尔积操作

笛卡尔积（Cartesian Product）是关系代数中的一种基础运算，记作“×”。其作用是生成两个关系的所有可能元组组合，即将第一个关系的每一个元组与第二个关系的每一个元组进行拼接，结果关系的属性为两个关系属性的并集，元组数为两个关系元组数的乘积。笛卡尔积通常作为连接（Join）等更复杂操作的基础。

设有如下两个关系：

笛卡尔积 教师 × 课程 的结果是：

在笛卡尔积的结果中，为了消除属性名的歧义，通常采用“关系名.属性名”的命名方式来标识每个属性。若教师关系包含 n 条元组，课程关系包含 m 条元组，则其笛卡尔积将产生 n×m 条元组。

需要注意的是，笛卡尔积通常作为后续关系操作（如连接）的基础步骤，而非最终查询目标。例如，若存在一个“授课”关系用于描述教师与课程的对应关系，则可以先对“教师”与“课程”执行笛卡尔积，再通过选择操作（σ）筛选出教师ID与授课关系匹配的元组，从而实现有意义的连接。

重命名操作

重命名（Renaming）操作是关系代数中的基本一元运算，记作希腊字母 ρ（rho）。其作用是为关系或其属性分配新的名称，以消除命名歧义或便于表达复杂查询，尤其在同一关系需要多次参与运算（如自连接）时尤为重要。

重命名操作的语法主要有两种形式。第一种形式仅对关系整体进行重命名：

第二种形式不仅重命名关系，还可以重命名其属性：

让我们看一个实际例子。假设我们想找出学校中薪资最高的教师。我们的策略是：

1. 首先找出所有不是最高薪资的教师薪资
2. 然后用差集操作找出最高薪资

要比较薪资，我们需要将教师表与自身进行比较，这就需要用到重命名操作，具体的关系代数表达式是：

这个表达式的含义是：从所有薪资中减去那些存在更高薪资的薪资值，剩下的就是最高薪资。

关系代数的正式定义

现在我们来给关系代数一个精确的数学定义。关系代数表达式由基础表达式逐步构建而成。 基础表达式包括：

• 数据库中的关系
• 常量关系（用大括号表示的元组集合）

例如，一个常量关系可以写成：

一般的关系代数表达式可以通过以下规则构建。如果E1和E2是关系代数表达式，那么以下也都是关系代数表达式：

这些规则确保了关系代数表达式的完整性和一致性，任何复杂的查询都可以通过组合这些基础操作来表达。

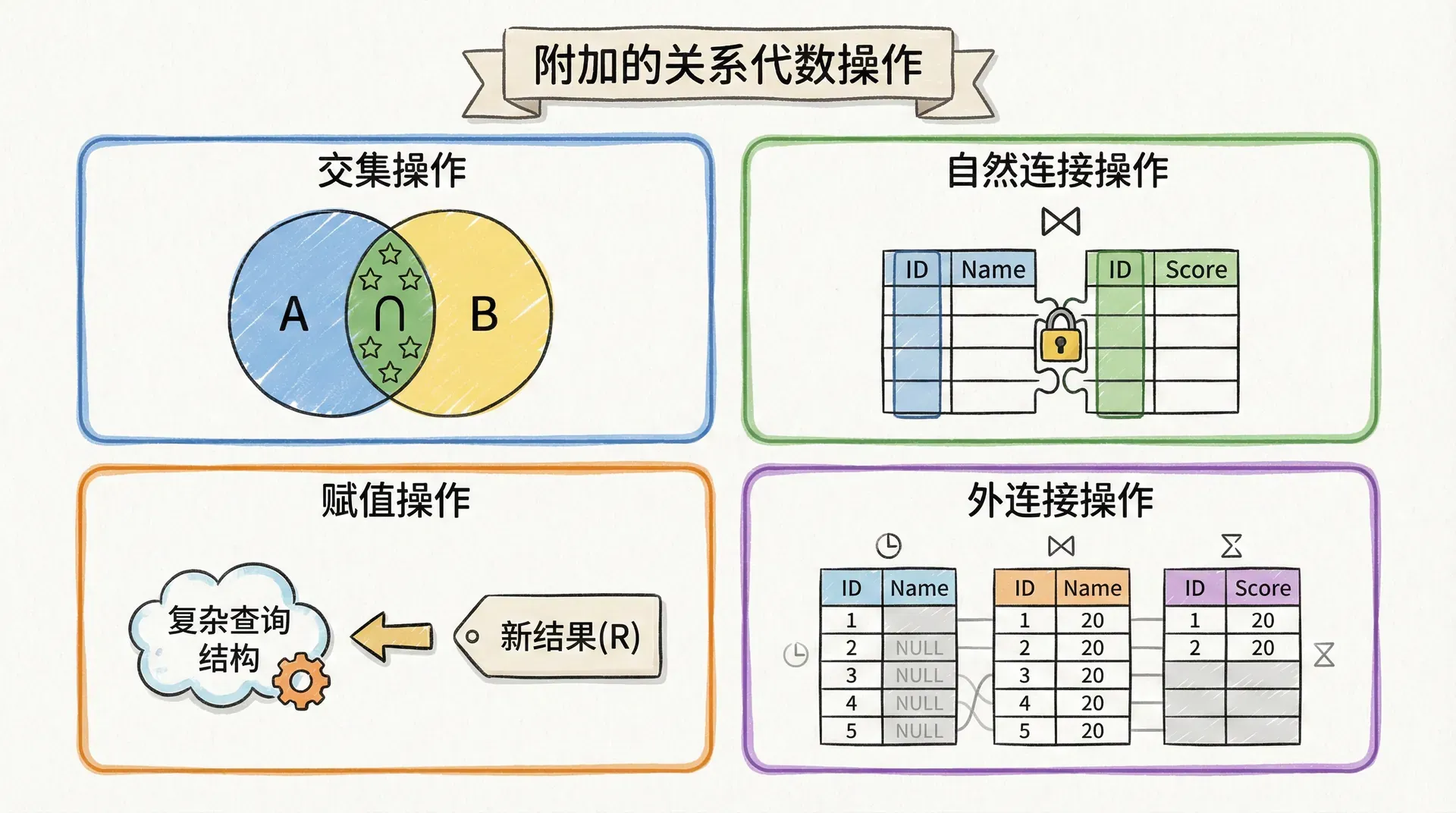
附加的关系代数操作

尽管基本操作已经能够表达所有关系查询，但在实际应用中，某些常见的查询模式往往导致表达式冗长且不便于理解。为提升表达的简洁性与可读性，关系代数引入了一些附加操作。 这些附加操作本质上属于语法糖，它们并未扩展关系代数的表达能力，均可通过基本操作进行等价转换。

交集操作

交集操作用∩表示，用来找出同时存在于两个关系中的记录。假设我们想找出既在2023年秋季学期又在2024年春季学期开设的课程：

交集操作可以用差集操作来表示：

该等式的数学含义为：通过从关系 r 中剔除属于 r 但不属于 s 的元组，最终保留的即为同时存在于 r 和 s 中的元组集合，即 r 与 s 的交集。

自然连接操作

自然连接（Natural Join）是关系数据库理论中的核心操作之一，记作符号 ⋈。它本质上是笛卡尔积与选择操作的结合，专门用于基于同名属性自动匹配并连接两个关系。

在执行自然连接时，系统会自动识别两个关系中所有同名属性，并仅保留这些属性取值相等的元组对。结果关系中，同名属性只保留一份，避免冗余。

例如，设有如下“教师”关系与“授课”关系：

教师 ⋈ 授课 的结果是：

注意教师ID属性只出现一次，因为自然连接会消除重复的属性。

用基础操作来表示自然连接，假设两个关系r(R)和s(S)有共同属性A1, A2, ..., An：

自然连接具有结合律性质，即：

这意味着我们可以写 r ⋈ s ⋈ t 而不需要担心操作顺序。

赋值操作

赋值操作用←符号表示，允许我们将中间结果保存到临时变量中，这样可以让复杂的查询表达式更易读和理解。

例如，之前找最高薪资的查询可以写成：

赋值操作不增加关系代数的表达能力，但它让复杂查询的逻辑更加清晰，也更符合我们编写程序的习惯。

外连接操作

外连接（Outer Join）是对自然连接的扩展，用于在连接操作中保留未能匹配的元组。在标准的自然连接中，只有两个关系中都存在匹配属性值的元组才会出现在结果中，未匹配的元组会被丢弃。外连接通过在结果中保留这些未匹配的元组，并将缺失部分用null填充，从而避免信息丢失。 外连接主要分为三类：

让我们用一个例子来说明。假设有些教师没有授课记录：

如果我们使用普通的自然连接 教师 ⋈ 授课，王教授的记录会消失，因为他没有授课记录。

但是用左外连接 教师 ⟕ 授课，结果会是：

这样我们就能看到所有教师，包括那些没有授课的教师。

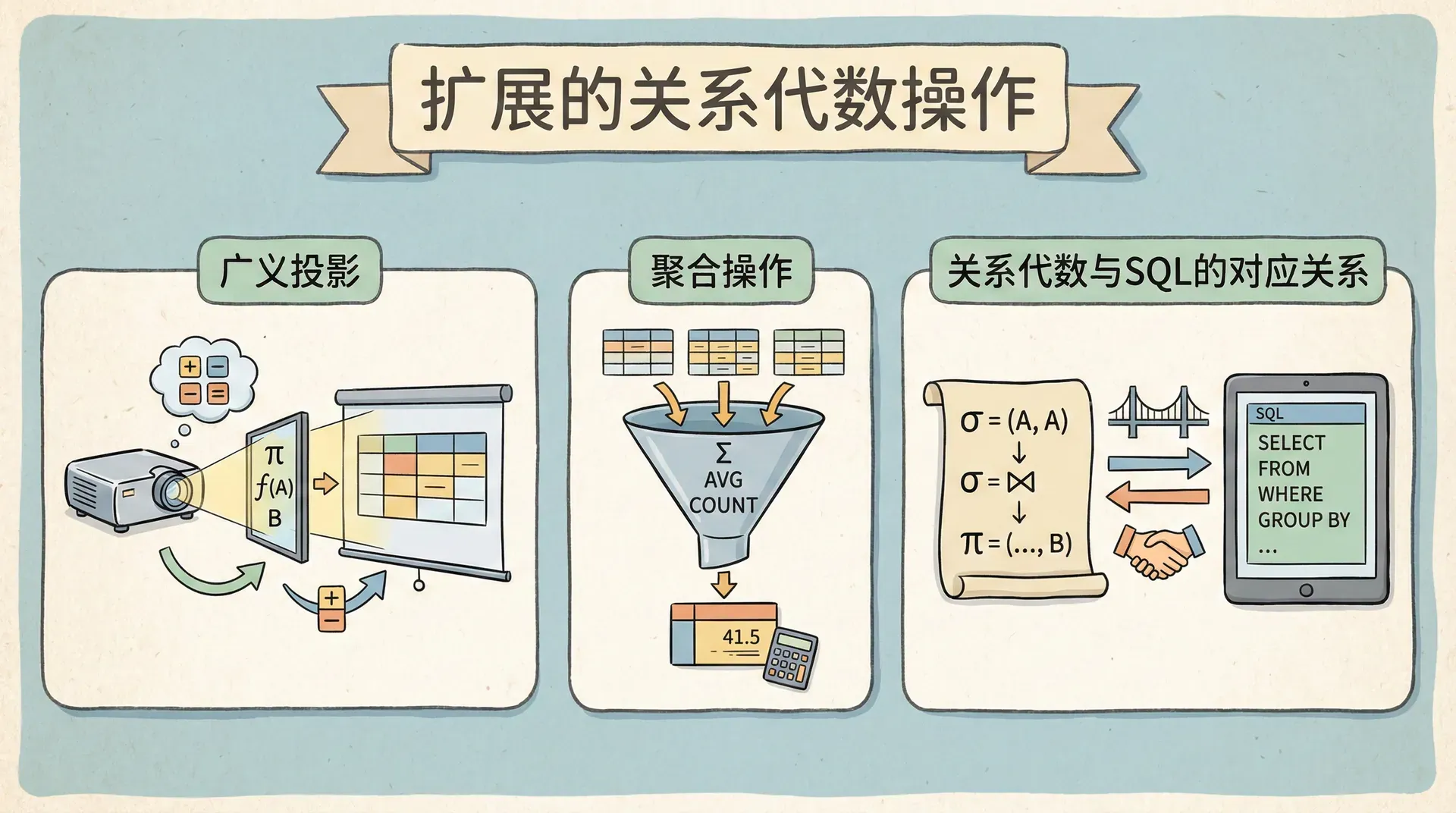
扩展的关系代数操作

基础的关系代数操作已经具备了完备的表达能力（即任意关系查询均可通过其实现），但在实际数据库应用中，常常需要进行更为复杂的数据处理与分析操作，例如统计汇总、分组聚合及算术运算等。 为满足这些高级需求，关系代数引入了扩展操作，进一步增强了其在数据分析与决策支持场景下的实用性和表达能力。

广义投影

广义投影扩展了普通的投影操作，允许在投影列表中使用算术表达式和函数。它的形式是：

其中每个F可以是：

• 简单的属性名
• 算术表达式
• 字符串函数
• 常量值

例如，如果我们想计算每个教师的月薪：

结果会包含一个新的列，显示每个教师的月薪。

聚合操作

聚合操作用符号G表示，允许我们对数据进行统计计算。常见的聚合函数包括：

最简单的聚合操作是对整个关系进行统计。例如，计算所有教师的薪资总和：

更常见的情况是按某些属性分组进行统计。例如，计算每个系的平均薪资：

这个操作会按系别对教师进行分组，然后计算每组的平均薪资：

聚合操作的一般形式是：

其中：

• G1, G2, ..., Gn 是分组属性
• F1, F2, ..., Fm 是聚合函数
• A1, A2, ..., Am 是参与计算的属性

当我们需要消除重复值时，可以在函数名后加上distinct。例如，统计有多少个不同的系在授课：

关系代数与SQL的对应关系

掌握关系代数的基本原理，有助于深入理解SQL查询语句的底层执行机制。以下是一个典型的SQL查询示例：

对应的关系代数表达式是：

这种对应关系帮助我们理解数据库系统是如何处理SQL查询的，也为查询优化提供了理论基础。

这个流程图展示了SQL查询的基本执行顺序，虽然实际的数据库系统会进行各种优化，但基本的逻辑框架是一致的。

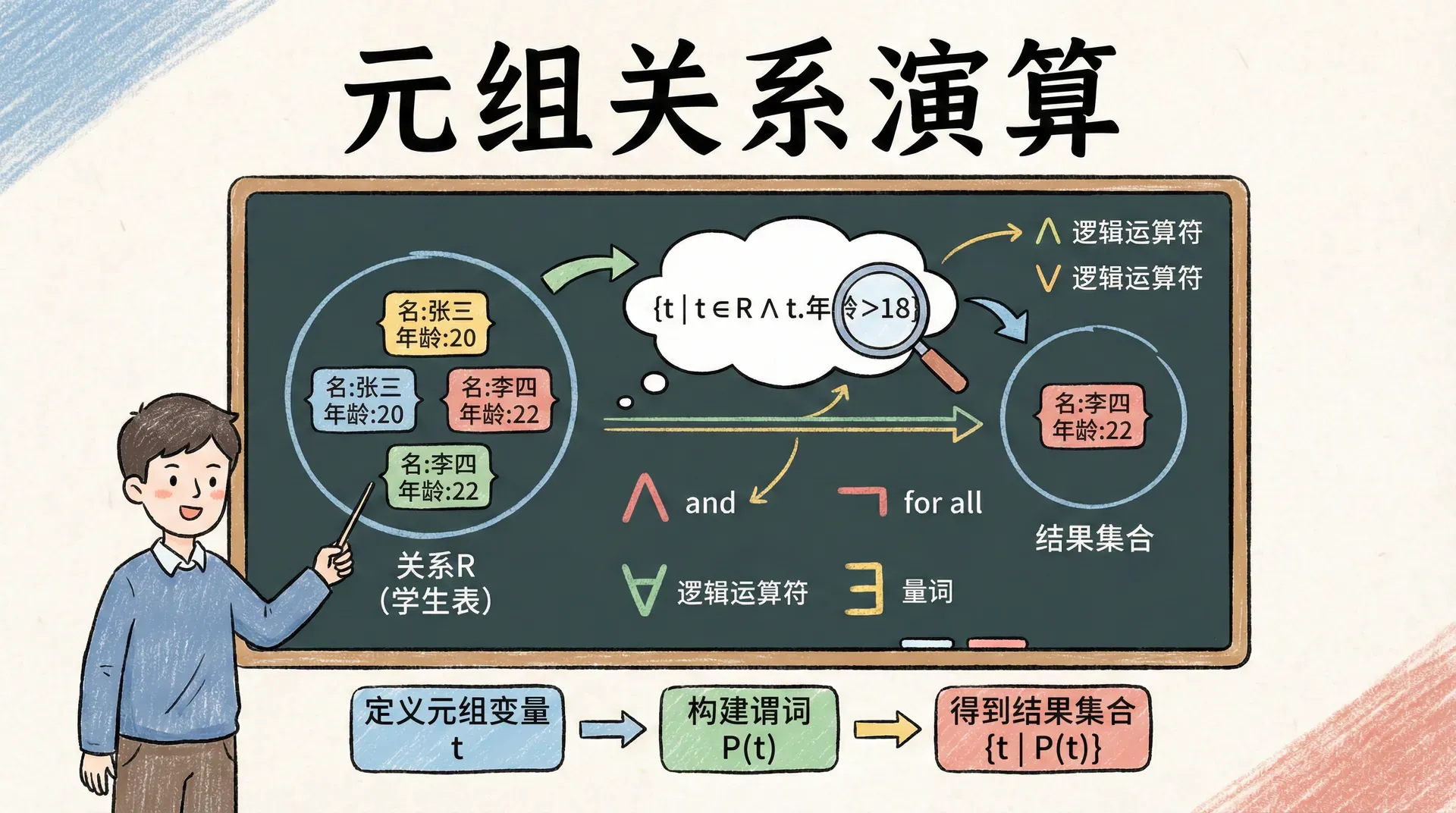
元组关系演算

元组关系演算（Tuple Relational Calculus, TRC）是一种基于一阶谓词逻辑的非过程化查询语言，与关系代数的操作性描述（即“如何执行”查询）不同，元组关系演算侧重于用逻辑公式描述查询结果应满足的性质（即“结果应具备什么特征”）。在元组关系演算中，用户通过指定元组变量及其应满足的谓词条件，来定义所需结果的集合，而无需关心具体的实现过程或操作顺序。

元组关系演算以数学逻辑为基础，采用逻辑表达式精确刻画目标数据的属性和约束，强调查询的声明性（declarative），即描述“是什么”，而非“如何做”。

基本概念和语法

元组关系演算的查询表达式具有以下形式：

该表达式表示“所有满足谓词P(t)的元组t的集合”。具体说明如下：

• t：元组变量，代表关系中的任意元组
• P(t)：逻辑谓词，对元组t施加的约束条件
• t[A]：表示元组t在属性A上的分量（即A属性的取值）
• t ∈ r：表示元组t属于关系r（即t是r的一个元素）

简单查询示例

让我们通过具体例子来理解元组关系演算的使用方法。

查询1：找出薪资超过80000的教师的所有信息

该表达式的语义为：选取所有属于“教师”关系且其“薪资”属性值大于80000的元组。

查询2：仅返回薪资超过80000的教师的ID属性

当查询目标仅涉及部分属性时，需引入存在量词（∃，exists）以实现属性投影：

该表达式的含义为：选取所有满足存在某个教师元组s，使得t[教师ID] = s[教师ID]且s[薪资] > 80000 的元组t，即实现对“教师”关系中薪资大于80000的教师ID属性的投影查询。

逻辑连接词的使用

元组关系演算采用一阶谓词逻辑中的标准逻辑联结词：

• ∧（合取，AND）：表示“且”，即所有条件同时成立时为真
• ∨（析取，OR）：表示“或”，即至少有一个条件成立时为真
• ¬（否定，NOT）：表示“非”，即条件不成立时为真

查询3：找出在2023年秋季学期或2024年春季学期开设的所有课程

多关系查询

当查询涉及多个关系时，我们需要使用多个存在量词。

查询4：找出在Watson大楼工作的所有教师姓名

该查询涉及两个存在量词：

• s 表示“教师”关系中的元组
• u 表示“部门”关系中的元组
• 通过“系别”属性实现两个关系的连接，实现连接操作的语义

全称量词的使用

除了存在量词∃，元组关系演算还使用全称量词∀（for all）。

查询5：找出学习了生物系所有课程的学生

该查询的逻辑可表述为：

1. t 代表某一学生的学号，需保证 t 确实对应学生关系中的一个元组；
2. 对于每一个属于生物系的课程 u，均要求存在一条选课关系 s，使得该学生（t）已选修该课程（u）。

其中，符号 ⇒（蕴含）表示“若...则...”，在形式逻辑中等价于 ¬P ∨ Q。

表达式的安全性

在元组关系演算中，表达式的“安全性”是一个核心理论问题。我们考虑如下表达式：

上述表达式旨在选取“所有不属于教师关系的元组”。然而，这样的表达式会产生无限多个元组，其中绝大多数元组包含数据库中并不存在的属性值。这种结果在实际数据库查询中是不可接受的。

为了解决这一问题，关系演算中引入了“安全表达式（safe expression）”的概念。对于表达式 {t | P(t)}，只有当其结果集合中的所有元组的属性值均来源于谓词 P 的“域（domain）”时，该表达式才被认为是安全的。这里，P 的域指的是：

• P 中出现的所有常量值；
• P 涉及的所有关系实例中实际出现的属性值。

安全性保证了查询结果的有限性和可计算性，是关系演算理论中的基本要求。

元组关系演算的表达能力

在理论计算机科学与数据库理论中，已严格证明元组关系演算（限定为安全表达式）与基础关系代数在表达能力上是等价的。具体而言：

• 任意一个关系代数表达式，均可构造出等价的元组关系演算表达式；
• 反之，任意一个安全的元组关系演算表达式，也都可以等价地用关系代数表达式表示。

这种等价性说明，两者在可表达的查询范围（即查询能力）上完全一致，仅在语法和思维范式上有所差异。关系代数采用过程式（operational）描述，强调数据处理的操作步骤；而元组关系演算则属于声明式（declarative）范式，侧重于描述查询的逻辑条件而非具体操作过程。

这个图表展示了三种形式化查询语言之间的等价关系，它们都具有相同的表达能力。

域关系演算

域关系演算（Domain Relational Calculus, DRC）是关系演算的另一种形式，其核心特征在于使用域变量（domain variable）而非元组变量。与元组关系演算（Tuple Relational Calculus, TRC）中变量代表整个元组不同，域关系演算中的每个变量仅代表单一属性值。换言之，DRC 直接对属性域上的取值进行逻辑约束和组合，从而描述查询条件。这种表达方式在理论上更贴近一阶谓词逻辑的范式。

域关系演算是 QBE（Query By Example）等图形化查询语言的理论基础，正如关系代数是 SQL 等主流关系型查询语言的理论支撑一样。DRC 的形式化定义和安全性约束在数据库理论与查询优化等领域具有重要意义。

基本概念和语法 —— 域关系演算

域关系演算的表达式具有以下形式：

其中：

• $x_1, x_2, \ldots, x_n$ 为域变量，每个变量取自相应属性的定义域，分别对应关系的各个属性值；
• $P$ 为谓词公式，由原子公式及逻辑联结词（）和量词（）递归构造而成，刻画元组需满足的约束条件；

域关系演算中的原子公式主要包括以下类型：

• $\langle x_1, x_2, \ldots, x_n \rangle \in r$：表示由域变量组成的元组属于关系 $$；

让我们通过具体例子来理解域关系演算的使用。

查询1：找出薪资超过80000的教师的ID、姓名、系别和薪资

这个表达式直接指定了我们想要的四个属性值，并要求它们组成的元组在教师关系中，且薪资大于80000。

查询2：只获取薪资超过80000的教师ID

注意这里的区别：在元组关系演算中，我们需要明确说明元组t的某个属性等于另一个元组s的某个属性；而在域关系演算中，我们直接使用域变量来表示具体的属性值。

域关系演算与元组关系演算的比较

虽然两种演算在表达能力上完全等价，但它们在思维模式上有所不同：

元组关系演算示例：

对应的域关系演算：

可以看出，域关系演算的表达更加直接和简洁。

安全性问题

域关系演算也面临与元组关系演算相同的安全性问题。表达式如：

该表达式会导致结果集为无穷大，因为存在无限多个不属于教师关系的四元组。 为保证查询的安全性，域关系演算对表达式施加了如下约束：

1. 查询结果中的所有取值必须限定于公式所涉及关系的域（active domain）；
2. 存在量词（∃）和全称量词（∀）的取值范围必须限定在有限的活动域内。

与QBE的关系

域关系演算为QBE（Query By Example）查询语言提供了理论支撑。QBE是一种基于表格模板的查询方式，用户通过在关系表的各属性列中填写变量、常量或条件，间接地构造出对应的逻辑查询表达式。这种交互式的查询建模方法本质上是对域关系演算的可视化实现，极大地提升了查询的表达能力与易用性：

这个QBE查询对应的域关系演算表达式就是：

实战演练

习题一：关系代数基础操作

假设我们有以下教师表（Teacher）：

使用关系代数表达式查询：计算机系中薪资超过75000的教授信息（只显示教师ID、姓名和薪资）。

习题二：并集与差集操作

设有以下两个课程安排表：

2023年秋季学期课程（Autumn2023）：

2024年春季学期课程（Spring2024）：

查询：在2024年春季学期开设但2023年秋季学期未开设的课程信息（显示课程ID、课程名和学分）。

习题三：自然连接操作

使用以下两个表进行查询：

教师表（Teacher）：

授课表（Teaches）：

查询：所有教师的授课信息，包括教师姓名、系别、课程ID和学期。

习题四：聚合操作

使用以下学生选课表（Enrolls）进行统计：

查询：每个课程的平均成绩（显示课程ID和平均成绩）。

习题五：元组关系演算

使用以下教师表：

用元组关系演算表示：查询薪资超过80000且入职年份早于2015年的教师姓名。

习题六：域关系演算

使用以下部门表和教师表：

部门表（Department）：

教师表（Teacher）：

用域关系演算表示：查询在理科楼工作的教授姓名。

习题七：复杂查询综合

使用以下完整的关系模式进行综合查询：

教师表（Teacher）：

课程表（Course）：

授课表（Teaches）：

查询：计算机系教师在2023年秋季学期教授的课程信息，包括教师姓名、课程名、学分和教室。

习题八：外连接操作

使用以下两个表，包含一些未匹配的数据：

教师表（Teacher）：

授课表（Teaches）：

查询：所有教师的授课情况，包括未授课的教师（显示教师姓名、系别、课程ID和学期，未授课的显示为null）。