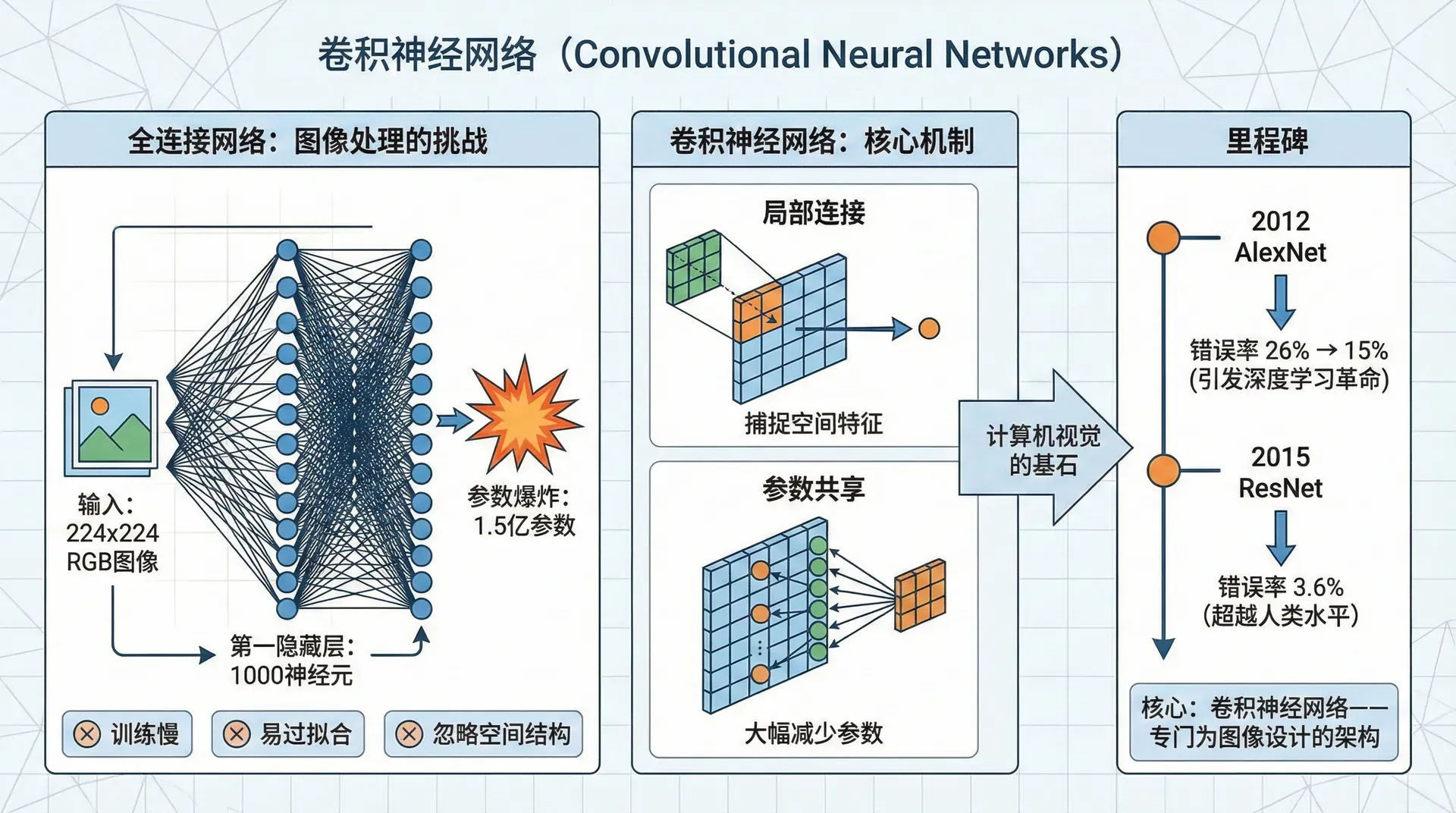
卷积神经网络

2012年ImageNet竞赛，AlexNet用卷积神经网络将错误率从26%降到15%，引发了深度学习革命。2015年，ResNet将错误率降到3.6%，超越了人类水平（5-10%）。这些突破的核心都是卷积神经网络——专门为图像设计的架构。

为什么全连接网络处理图像效果不好？一张224×224的RGB图片有150,528个像素。第一个隐藏层如果有1000个神经元，参数量就是1.5亿——训练慢、容易过拟合，而且忽略了图像的空间结构。卷积网络通过参数共享和局部连接解决了这些问题，成为计算机视觉的基石。

卷积操作

卷积（Convolution）是卷积网络的核心操作。想象你要检测图像中的垂直边缘。一个简单的3×3滤波器（也叫卷积核）能完成这个任务：

将这个滤波器在图像上滑动，每个位置做元素wise乘法然后求和。左边亮右边暗的区域会产生大的响应，就检测到了垂直边缘。

数学定义：给定输入图像 $I$ 和滤波器 $K$，卷积结果在位置 $(i,j)$ 的值是：

|
import numpy as np
 
def convolve2d(image, kernel):
    """
    2D卷积（简化版，不考虑padding）
    image: (H, W)
    kernel: (K, K)
    """
    H, W = image.shape
    K = kernel.shape[0]
    output_H = H - K + 1
    output_W = W - K + 1
    
    output = np.zeros((output_H, output_W))

类似地，水平边缘检测器是：

传统计算机视觉会手工设计这些滤波器。深度学习的革命性想法是：让网络自己学习滤波器。卷积核的权重不是固定的，而是通过反向传播学习的参数。网络会学到比人工设计更好的特征检测器。

Padding和Stride

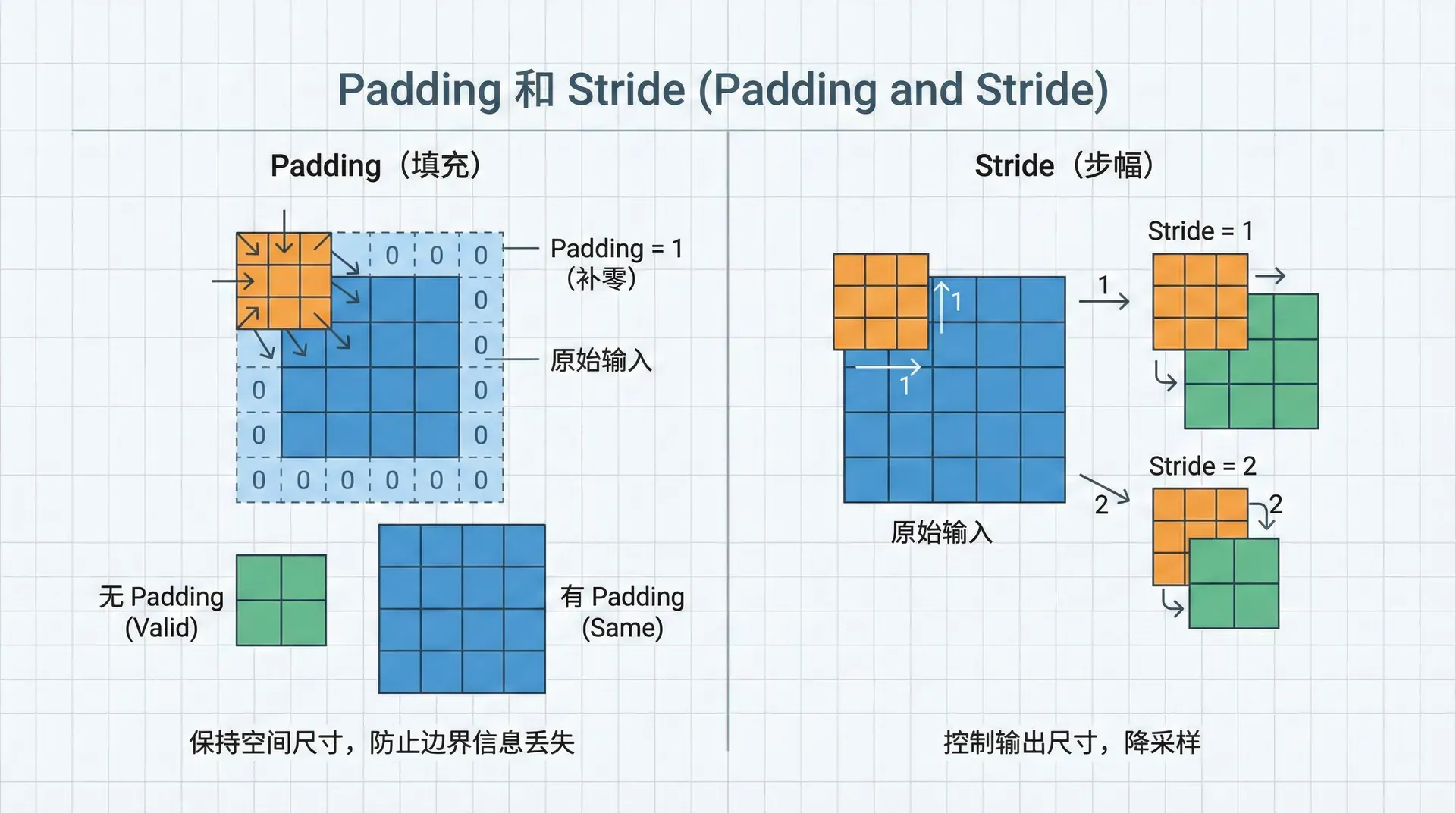
卷积有个问题：输出比输入小。一个 $n \times n$ 的图像与 $f \times f$ 的滤波器卷积，输出是 $(n-f+1) \times (n-f+1)$。多层卷积后图像会越来越小。

Padding通过在图像边缘填充像素解决这个问题。最常用的是“Same”卷积：padding后输出与输入同大小。

有效卷积（Valid）：不padding，输出为 $(n-f+1) \times (n-f+1)$

相同卷积（Same）：padding使输出为 $n \times n$。padding大小为 $p = \frac{f-1}{2}$（假设 $f$ 是奇数）

Stride（步长）控制滤波器移动的步长。stride=1是每次移动一个像素，stride=2是每次移动两个像素（跳过一些位置）。

输出大小公式：

其中 $n$ 是输入大小，$p$ 是padding，$f$ 是滤波器大小，$s$ 是stride。

|
def conv2d_with_padding_stride(image, kernel, padding=0, stride=1):
    """带padding和stride的2D卷积"""
    H, W = image.shape
    K = kernel.shape[0]
    
    # 添加padding
    if padding > 0:
        image_padded = np.pad(image, padding, mode='constant')
    else:
        image_padded = image
    

多通道卷积

RGB图像有3个通道。卷积核也需要3个通道，每个通道一个滤波器，然后将三个通道的结果相加：

输入：$(n_H, n_W, n_C)$，如 $(32, 32, 3)$

滤波器：$(f, f, n_C, n_{C_{out}})$，如 $$ 表示16个3×3×3的滤波器

输出：$(n_H', n_W', n_{C_{out}})$，如

每个滤波器产生一个输出通道。16个滤波器产生16个特征图。

|
def conv2d_multi_channel(X, W, b, padding=1, stride=1):
    """
    多通道卷积
    X: (H, W, C_in)
    W: (f, f, C_in, C_out)
    b: (C_out,)
    """
    H, W, C_in = X.shape
    f, _, _, C_out = W.shape
    
    # Padding
    X_padded = np.pad(X, ((padding, padding), (padding, padding), (0, 0)), mode='constant')
    
    # 输出大小

池化层

池化（Pooling）操作降低特征图的空间维度，减少参数量和计算量，同时提供平移不变性。

最大池化（Max Pooling）：取窗口内的最大值

平均池化（Average Pooling）：取窗口内的平均值

典型配置：2×2窗口，stride=2，将特征图大小减半。

|
def max_pool2d(X, pool_size=2, stride=2):
    """
    最大池化
    X: (H, W, C)
    """
    H, W, C = X.shape
    H_out = (H - pool_size) // stride + 1
    W_out = (W - pool_size) // stride + 1
    
    output = np.zeros((H_out, W_out, C))
    

池化层没有可学习的参数，只是一个固定的操作。它的作用是：

• 降低计算量：特征图变小
• 增加感受野：后续层能"看到"更大的图像区域
• 提供不变性：小的平移不影响结果

完整的CNN架构

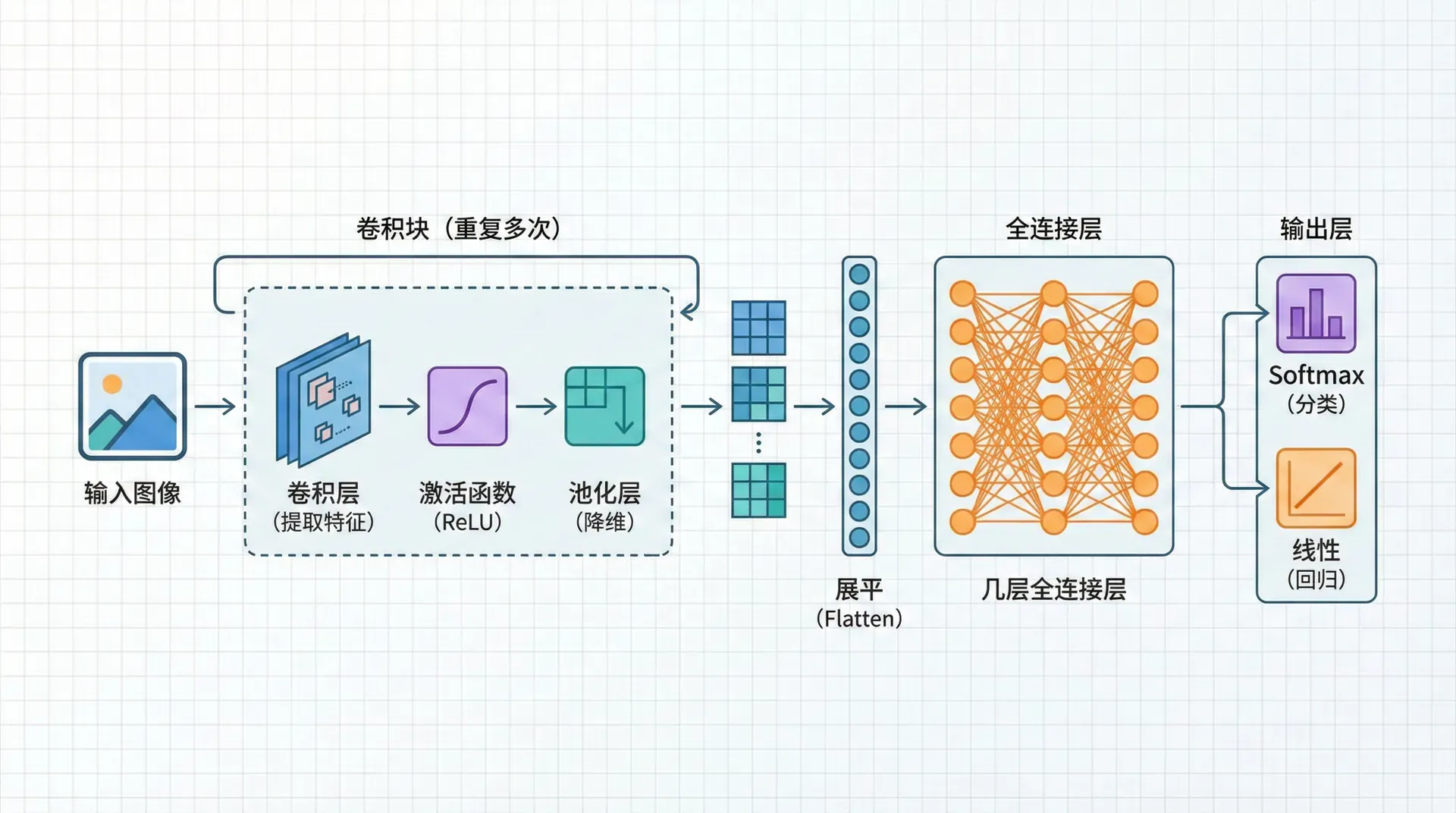
一个典型的CNN由以下模块组成：

卷积块（重复多次）：

• 卷积层：提取特征
• 激活函数：通常是ReLU
• 池化层：降维

全连接层：

• 将特征图展平
• 几层全连接层
• 输出层：Softmax（分类）或线性（回归）

|
def simple_cnn(X, parameters):
    """
    简单的CNN前向传播
    Conv -> ReLU -> Pool -> Conv -> ReLU -> Pool -> FC -> FC -> Softmax
    """
    # 第一个卷积块
    Z1 = conv2d_multi_channel(X, parameters['W1'], parameters['b1'])
    A1 = relu(Z1)
    P1 = max_pool2d(A1)
    
    # 第二个卷积块
    Z2 = conv2d_multi_channel(P1, parameters['W2'], parameters['b2'])
    A2 = relu(Z2)
    P2 = max_pool2d(A2)

参数共享和稀疏连接

为什么CNN比全连接网络好？两个关键特性：

参数共享：同一个滤波器在整个图像上滑动，共享同一组权重。一个检测垂直边缘的滤波器在左上角有用，在右下角也有用，不需要学两遍。

对比：全连接网络中，每个神经元都有独立的权重，无法共享。

稀疏连接：每个输出神经元只连接输入的一小块区域（感受野），而不是全部输入。一个3×3的滤波器只有9个连接，而全连接层有 $n_x$ 个连接。

这两个特性带来的好处：

• 更少的参数：100倍甚至1000倍的参数减少
• 更少的计算：训练和推理更快
• 更好的泛化：参数少不容易过拟合
• 平移不变性：物体在图像中移动，网络仍能识别

实际数据：AlexNet有6000万参数，但如果用全连接网络处理同样大小的图像，需要数十亿参数。

在下一节，我们将学习经典的CNN架构——LeNet、AlexNet、VGG、ResNet、Inception。这些里程碑式的网络不仅在当时取得了最好成绩，更重要的是引入了影响深远的设计理念：深度的重要性、残差连接、Inception模块等。理解这些经典架构，能帮助你设计自己的网络。