线性回归

在刚刚的学习中，我们了解了机器学习的基本概念和主要分类。现在，让我们深入学习第一个具体的机器学习算法——线性回归。线性回归不仅是最简单、最基础的机器学习算法之一，它还蕴含着机器学习的核心思想：如何用数学模型描述数据，如何定义模型的好坏，如何通过优化算法找到最优模型。

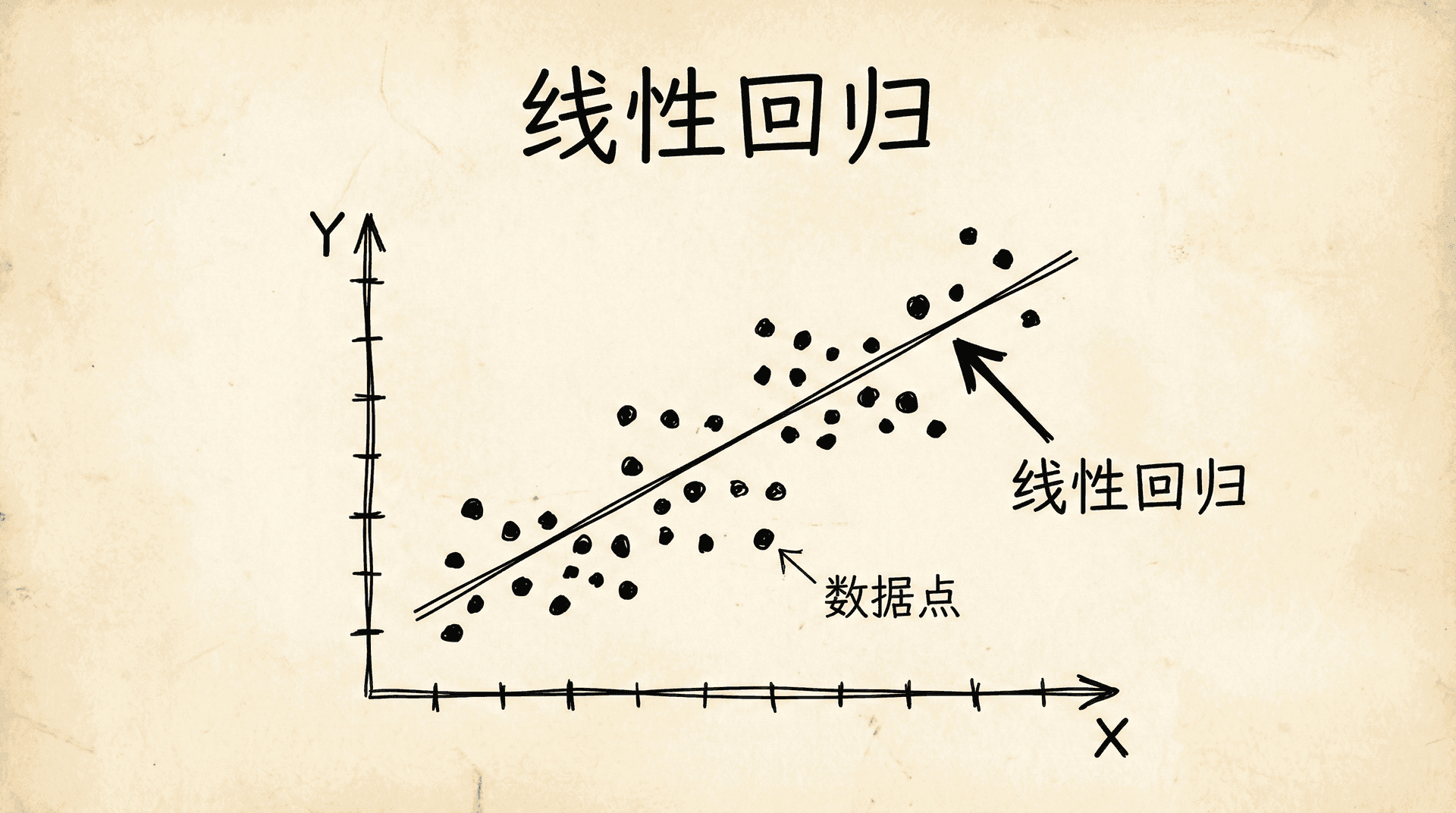
假设我们在一家房地产公司工作，老板希望我们能够根据房屋的面积来预测房价。我们手里有过去几个月的交易数据：一套50平方米的房子卖了150万，一套80平方米的卖了240万，一套100平方米的卖了300万……我们的任务是，给定一套新房子的面积，预测它能卖多少钱。这就是一个典型的线性回归问题。

用数学语言描述预测问题

当我们面对房价预测这样的问题时，直觉告诉我们，房价和面积之间似乎存在某种关系。更大的房子通常更贵，这是一个朴素的观察。但如何把这种模糊的感觉变成精确的数学表达呢？这就是模型的作用。

在机器学习中，模型就是一个数学函数，它接受输入（房屋面积），产生输出（预测的房价）。对于线性回归，我们假设输出和输入之间存在线性关系。用数学符号表示，就是：

$h_\theta(x) = \theta_0 + \theta_1 x$

这个公式看起来很像我们在中学学过的直线方程 $y = mx + b$。这里的 $h_\theta(x)$ 表示我们的假设函数（hypothesis function），也就是我们的预测模型。$x$ 是输入特征，在我们的例子中就是房屋面积。$\theta_0$ 和 是模型的参数， 是截距（当面积为0时的房价，虽然这在现实中没有意义，但数学上需要这一项）， 是斜率（面积每增加1平方米，房价增加多少）。

为什么叫“假设”函数？因为我们在假设房价和面积之间是线性关系。这个假设可能准确，也可能不够准确，但这是我们开始解决问题的起点。通过这个假设，我们把一个模糊的预测问题转化成了一个明确的数学问题：找到合适的 $\theta_0$ 和 $\theta_1$，使得这条直线能够很好地拟合我们的数据。

让我们用具体的数字来理解。假设通过某种方法，我们确定了 $\theta_0 = 50$，$\theta_1 = 2.5$。那么我们的模型就是：

$h_\theta(x) = 50 + 2.5x$

这个模型告诉我们，基础房价是50万（$\theta_0$），然后每平方米增加2.5万（$\theta_1$）。如果有一套70平方米的房子，我们的预测就是：

$h_\theta(70) = 50 + 2.5 \times 70 = 225 \text{万元}$

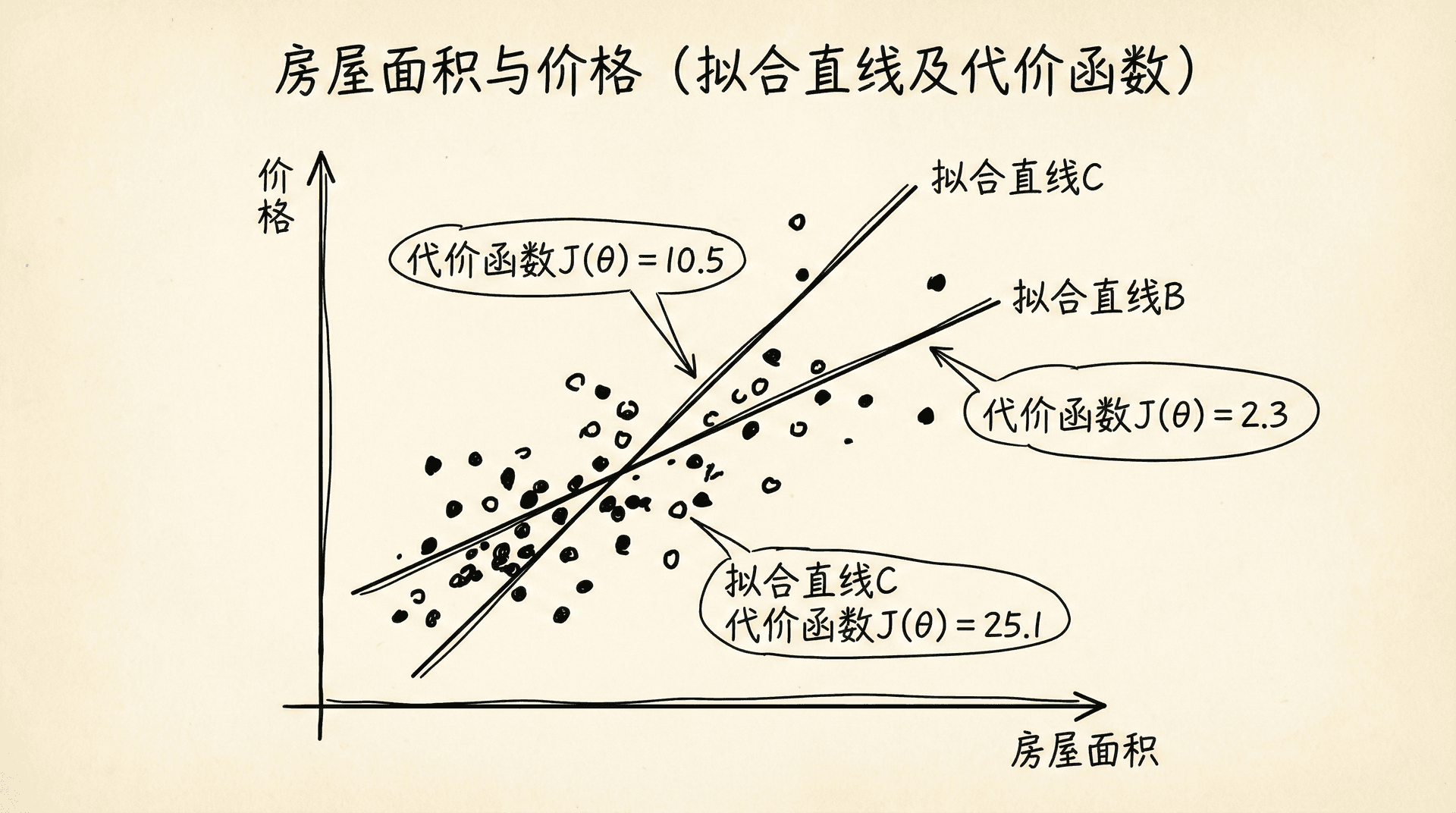
这就是线性回归模型的工作方式。但问题来了：我们如何确定 $\theta_0$ 和 $\theta_1$ 的值？不同的参数值会给出不同的直线，不同的直线对数据的拟合程度不同。我们需要一个标准来衡量哪条直线是最好的，这就引出了代价函数的概念。

在深入代价函数之前，让我们先建立一些符号约定。我们用 $m$ 表示训练样本的数量，$x^{(i)}$ 表示第 $i$ 个训练样本的输入特征，$y^{(i)}$ 表示第 $i$ 个训练样本的实际输出（真实房价）。注意这里的上标 不是指数，而是索引，表示第几个样本。训练集就是所有的 对，。

我们的目标是，找到合适的参数 $\theta_0$ 和 $\theta_1$，使得对于所有的训练样本，$h_\theta(x^{(i)})$ 尽可能接近 。换句话说，我们希望模型的预测值和真实值之间的差距尽可能小。

衡量模型好坏的标准

想象我们在射击靶子，每次射击都会留下一个弹孔。衡量射击水平的一个方法是看所有弹孔距离靶心的平均距离。在机器学习中，我们也需要类似的方法来衡量模型的预测与真实值之间的差距。这个衡量标准就是代价函数（Cost Function），也叫损失函数（Loss Function）。

对于线性回归，最常用的代价函数是均方误差（Mean Squared Error）：

$J(\theta_0, \theta_1) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2$

让我们仔细拆解这个公式。$(h_\theta(x^{(i)}) - y^{(i)})$ 是第 $i$ 个样本的预测误差，也就是预测值和真实值的差。我们把这个差平方（），这样做有两个好处：一是消除了正负号，二是对较大的误差给予更大的惩罚。然后我们把所有样本的平方误差加起来（），再除以样本数量 ，得到平均值。前面的 是为了后续求导时计算方便（平方项求导会出现一个2，正好与这里的 抵消）。

代价函数 $J(\theta_0, \theta_1)$ 的值反映了当前参数下模型的表现。$J$ 的值越小，说明模型的预测越准确；$J$ 的值越大，说明模型的预测误差越大。我们的目标就是找到使 $J({\theta }_0,{\theta }_1)$ 最小的参数值。

让我们用一个简化的例子来建立直觉。假设我们只有三个数据点：$(1, 1)$，$(2, 2)$，$(3, 3)$。为了简化，我们先假设 $\theta_0 = 0$，只考虑参数 。这样模型就变成了 ，一条过原点的直线。

如果我们选择 $\theta_1 = 1$，那么：

• 对于 $x^{(1)} = 1$，预测值是 $h_\theta(1) = 1$，真实值是 $y^{(1)} = 1$，误差是0

代价函数 $J(1) = \frac{1}{6}(0^2 + 0^2 + 0^2) = 0$。这是完美拟合！

如果我们选择 $\theta_1 = 0.5$，那么：

• 对于 $x^{(1)} = 1$，预测值是0.5，误差是 $0.5 - 1 = -0.5$
• 对于 $x^{(2)} = 2$，预测值是1，误差是

代价函数 $J(0.5) = \frac{1}{6}(0.25 + 1 + 2.25) = 0.583$。这个拟合就差多了。

代价函数的几何意义

当我们只有一个参数 $\theta_1$（假设 $\theta_0 = 0$）时，代价函数 $J(\theta_1)$ 是关于 的函数。我们可以画出 随 变化的曲线。通常，这个曲线是一个碗状的抛物线，在某个 值处达到最小值。那个最小值点对应的 就是我们要找的最优参数。

当我们有两个参数 $\theta_0$ 和 $\theta_1$ 时，代价函数 $J(\theta_0, \theta_1)$ 是一个关于两个变量的函数。它的图形是一个三维的曲面，看起来像一个碗或者山谷。在某个点 处，这个曲面有一个最低点，那就是代价函数的最小值。我们的目标就是找到这个最低点。

从另一个角度看，我们可以画出代价函数的等高线图。等高线上的每个点都有相同的代价函数值。在等高线图中，最优参数位于等高线的中心，就像地形图中的谷底。

这种几何理解很重要，因为它帮助我们直观地理解优化问题的本质：在参数空间中寻找代价函数的最小值点。不同的参数组合对应参数空间中的不同位置，每个位置都有一个代价函数值。我们需要在这个空间中导航，找到代价函数最小的那个位置。

|
# 计算代价函数的示例代码
def computeCost(X, y, theta):
    """
    计算线性回归的代价函数
    X: 特征矩阵，m x n（m个样本，n个特征）
    y: 标签向量，m x 1
    theta: 参数向量，n x 1
    """
    m = len(y)  # 样本数量
    
    # 计算预测值
    predictions = X.dot(theta)
    
    # 计算误差
    errors = predictions - y
    
    # 计算代价函数
    J = (1 / (

理解代价函数是理解机器学习的关键一步。代价函数不仅告诉我们模型的好坏，更重要的是，它为我们提供了优化的目标。在有了明确的优化目标后，下一个问题就是：如何找到使代价函数最小的参数？这就引出了梯度下降算法。

寻找最优解的核心算法

想象你站在一座雾蒙蒙的山上，看不清周围的地形，你的目标是走到山脚（最低点）。一个自然的策略是：感受脚下的坡度，朝着最陡的下坡方向迈一步，然后重复这个过程，直到到达平地。这就是梯度下降算法的核心思想。

梯度下降（Gradient Descent）是机器学习中最重要的优化算法之一。它的基本思路非常简单：从某个初始参数开始，反复调整参数，每次都朝着代价函数下降最快的方向移动一小步，最终到达代价函数的最小值点。

梯度下降的更新规则是：

$\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1)$

这里 $:=$ 表示赋值，$\alpha$ 是学习率（learning rate），控制每次更新的步长。$\frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1)$ 是代价函数对参数 的偏导数，也就是在当前位置代价函数的梯度。

让我们理解这个公式的每个部分。偏导数 $\frac{\partial}{\partial \theta_j} J$ 告诉我们，当 $\theta_j$ 增加一点点时，代价函数 会如何变化。如果偏导数是正的，说明增加 会使 增大，那么我们应该减小 ；如果偏导数是负的，说明增加 会使 减小，那么我们应该增加 。注意更新规则中的负号，它确保了我们总是朝着代价函数下降的方向移动。

学习率 $\alpha$ 控制每次移动的步长。如果 $\alpha$ 太小，算法会非常缓慢地收敛，需要很多次迭代才能到达最小值。如果 $\alpha$ 太大，可能会跨过最小值点，甚至导致算法发散，代价函数不降反升。选择合适的学习率是使用梯度下降时的一个重要技巧。

让我们看一个具体的例子。假设我们的代价函数在当前参数下的梯度是 $\frac{\partial J}{\partial \theta_1} = 0.5$，学习率 $\alpha = 0.1$，当前参数值 。那么下一步的更新是：

$\theta_1 := 1 - 0.1 \times 0.5 = 0.95$

我们把 $\theta_1$ 从1调整到了0.95，朝着代价函数减小的方向移动了一步。然后我们在新的参数值处重新计算梯度，继续更新，如此反复。

梯度下降有一个美妙的性质：随着我们接近最小值点，梯度会自动变小。这意味着即使学习率保持不变，更新的步长也会自动减小，算法会更加平稳地收敛。当到达最小值点时，梯度变为零，参数不再更新，算法自然停止。

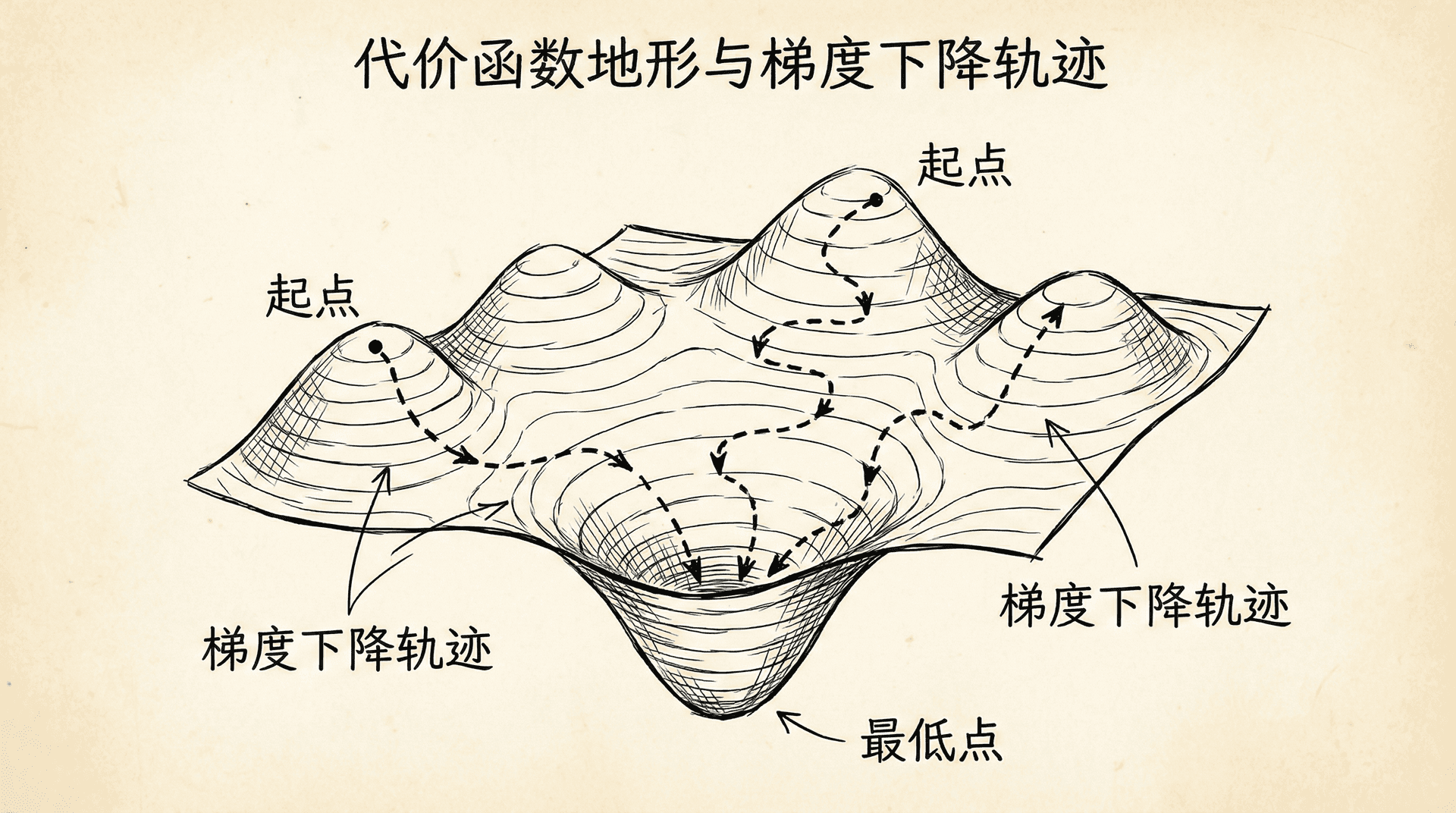
在实践中，我们通常会设定一些停止条件来判断算法是否收敛。常见的停止条件包括：代价函数的改变量小于某个阈值（说明已经接近最小值），梯度的范数小于某个阈值（说明已经在平坦的地方），或者达到了预设的最大迭代次数。

梯度下降的一个重要变种是批量梯度下降（Batch Gradient Descent）。在每次更新参数时，我们使用所有的训练样本来计算梯度。这就是我们目前讨论的版本。批量梯度下降的优点是每次更新的方向都是准确的，沿着代价函数真正下降最快的方向。缺点是当训练集很大时，每次迭代都要遍历所有数据，计算量很大。

为了解决这个问题，后续我们会学习随机梯度下降（Stochastic Gradient Descent）和小批量梯度下降（Mini-batch Gradient Descent），它们每次只使用一部分数据来计算梯度，大大提高了计算效率。

将梯度下降应用到线性回归

现在我们把梯度下降算法应用到线性回归问题上。对于线性回归，我们的代价函数是：

$J(\theta_0, \theta_1) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2$

其中 $h_\theta(x) = \theta_0 + \theta_1 x$。为了使用梯度下降，我们需要计算代价函数对每个参数的偏导数。通过微积分，我们可以得到：

$\frac{\partial}{\partial \theta_0} J(\theta_0, \theta_1) = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})$

$\frac{\partial}{\partial \theta_1} J(\theta_0, \theta_1) = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x^{(i)}$

这两个公式看起来很相似，唯一的区别是对 $\theta_1$ 的偏导数多了一个 $x^{(i)}$ 项。直观理解，$\theta_0$ 控制的是截距，影响所有点的预测值；${}_{}$ 控制的是斜率，对于 值较大的点影响更大，所以梯度要乘以 。

有了这些偏导数，梯度下降的更新规则就变成：

$\theta_0 := \theta_0 - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})$

$\theta_1 := \theta_1 - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x^{(i)}$

记住，这两个更新要同时进行。完整的算法流程是：

1. 初始化参数 $\theta_0$ 和 $\theta_1$（通常初始化为0或随机小值）
2. 重复以下步骤，直到收敛：
   • 计算所有样本的预测值 $h_\theta(x^{(i)})$

让我们通过一个具体的例子来演示这个过程。假设我们有如下训练数据：

初始化 $\theta_0 = 0$，$\theta_1 = 0$，学习率 $\alpha = 0.01$。

第一次迭代：

• 所有预测值都是0（因为 $h_\theta(x) = 0 + 0 \cdot x = 0$）
• 误差分别是：$-150, -180, -200, -240$

经过多次迭代后，参数会逐渐收敛到最优值。在这个例子中，最优解大约是 $\theta_0 \approx 30$，$\theta_1 \approx 2.5$，对应的模型是 $h_\theta(x) = 30 + 2.5x$。

|
# 线性回归梯度下降的完整实现
def gradientDescent(X, y, theta, alpha, numIterations):
    """
    使用梯度下降优化线性回归参数
    X: 特征矩阵（包含了x0=1的列）
    y: 标签向量
    theta: 初始参数
    alpha: 学习率
    numIterations: 迭代次数
    """
    m = len(y)  # 样本数量
    J_history = []  # 记录每次迭代的代价函数值
    
    for iteration in range(numIterations):
        # 计算预测值
        predictions = X.dot(theta)
        
        # 计算误差

|
最优参数: θ0 = 0.05, θ1 = 2.96

在实际应用中，我们还需要关注一些实践细节。学习率的选择至关重要。一个好的做法是尝试多个学习率（比如0.001, 0.003, 0.01, 0.03, 0.1等），观察代价函数的下降曲线，选择既收敛快又稳定的学习率。

特征的尺度也会影响梯度下降的效果。如果不同特征的取值范围差异很大（比如面积在几十到几百，而价格在几十万到几百万），梯度下降可能会很慢。特征缩放（Feature Scaling）可以解决这个问题，我们会在后续章节详细讨论。

监控收敛过程也很重要。我们应该画出代价函数随迭代次数变化的曲线。如果曲线平滑下降并趋于平稳，说明算法正常收敛。如果曲线震荡或上升，可能是学习率太大。如果曲线下降很慢，可能是学习率太小。

线性回归可视化

线性回归的几何解释与扩展思考

从几何角度看，线性回归就是在数据点中找一条“最佳拟合”的直线。这条直线使得所有点到它的距离平方和最小。在二维情况下，我们可以直观地看到数据点散布在平面上，直线穿过点云，尽量靠近每个点。在高维情况下（多个特征），“直线”变成了“超平面”，但原理是一样的。

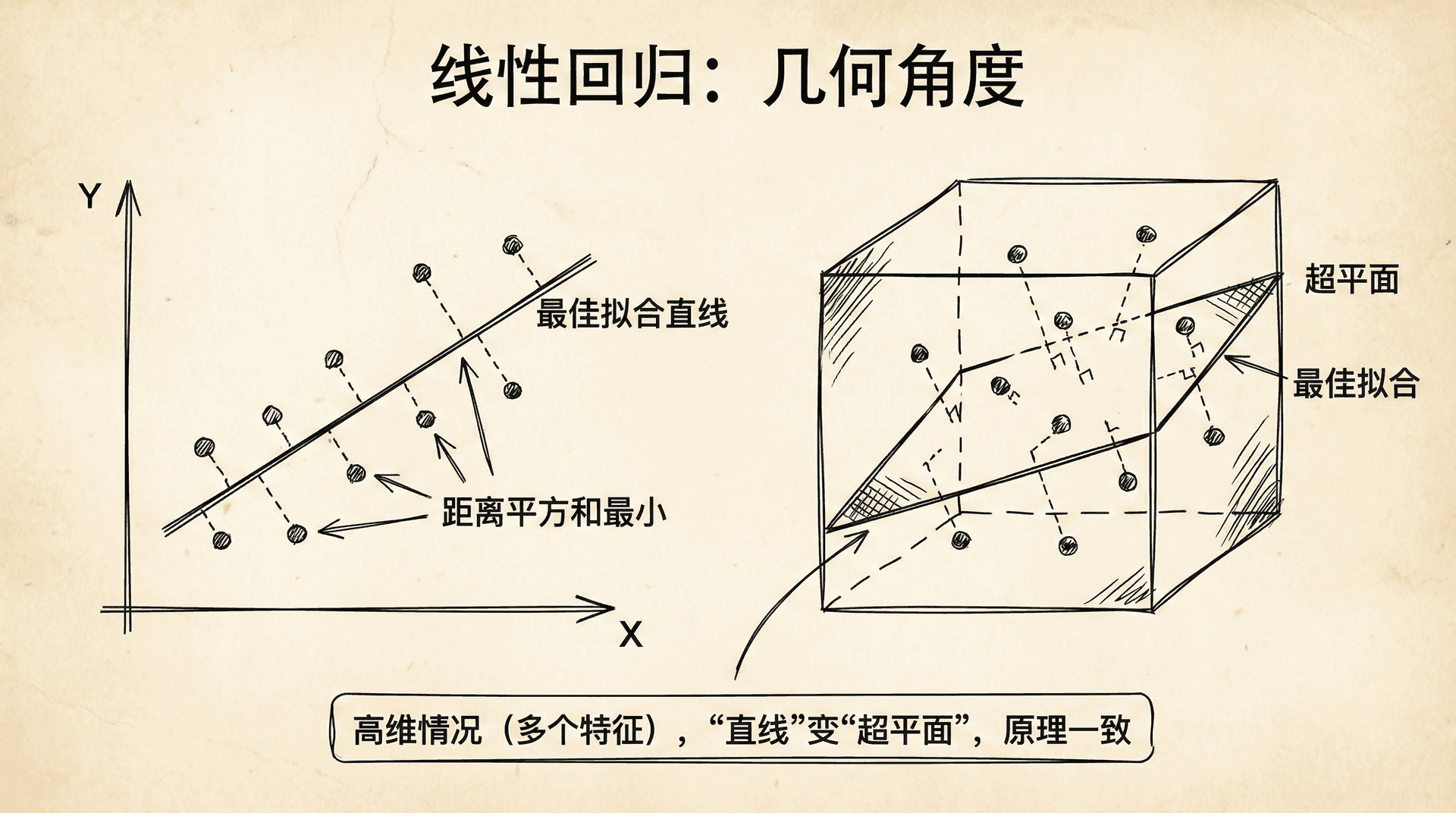
线性回归的强大之处不仅在于它的简单，更在于它的可扩展性。虽然模型形式简单，但通过特征工程，我们可以用线性回归处理复杂的非线性关系。 比如，如果我们认为房价与面积的关系不是线性的，而是二次的，我们可以构造新特征 $x^2$，然后用线性回归拟合 $h_\theta(x) = \theta_0 + \theta_1 x + \theta_2 x^2$。虽然这对原始特征 来说是非线性的，但对参数 来说仍然是线性的，所以仍然可以用线性回归的方法求解。

线性回归也有其局限性。它假设输入和输出之间存在线性关系，这个假设在很多情况下并不成立。它对异常值（outliers）很敏感，因为误差是平方的，大的误差会被放大。它假设误差服从正态分布且方差恒定，这些假设在实际数据中可能不满足。

尽管有这些局限，线性回归仍然是最常用的机器学习算法之一。它计算效率高，结果易于解释（我们可以清楚地看到每个特征对输出的影响），在很多实际问题中表现良好。更重要的是，它是理解更复杂算法的基础。逻辑回归、神经网络、支持向量机等算法都可以看作是线性回归的扩展或变形。

在结束这一部分的学习之前，让我们回顾线性回归的整个流程。我们从一个实际问题（预测房价）出发，提出了一个数学模型（线性假设函数），定义了评价标准（均方误差代价函数），使用了优化算法（梯度下降）来找到最优参数。这个完整的流程体现了机器学习解决问题的基本思路：建模、优化、评估。

在下一部分的学习中，我们会复习一些线性代数的知识。为什么要复习线性代数？因为当我们处理多个特征的线性回归时，用矩阵和向量来表示会使公式更加简洁，计算更加高效。线性代数是机器学习的数学语言，掌握它会让我们对算法有更深的理解，也能更有效地实现算法。

小练习

1. 手动计算代价函数：假设我们有以下3个训练样本，用于预测房价（单位：万元）：

   面积 (x, 平方米)	房价 (y, 万元)
   50	150
   80	200
   100	250

   如果我们的模型是 $h_\theta(x) = \theta_0 + \theta_1 x$，参数为 ，。请计算代价函数 的值。

2. 梯度下降参数更新：继续使用上一题的数据和模型。假设当前参数为 $\theta_0 = 50$，$\theta_1 = 2$，学习率 $\alpha = 0.01$。请执行一次梯度下降迭代，计算更新后的 和 的值。

这里 $m = 3$（3个样本）。让我们逐步计算：

步骤1：计算每个样本的预测值

• 样本1：$h_\theta(50) = 50 + 2 \times 50 = 150$ 万元
• 样本2：$h_\theta(80) = 50 + 2 \times 80 = 210$ 万元
• 样本3：$h_\theta(100) = 50 + 2 \times 100 = 250$ 万元

步骤2：计算每个样本的预测误差

• 样本1：$h_\theta(50) - y^{(1)} = 150 - 150 = 0$
• 样本2：$h_\theta(80) - y^{(2)} = 210 - 200 = 10$
• 样本3：$h_\theta(100) - y^{(3)} = 250 - 250 = 0$

步骤3：计算误差平方和 $\sum_{i=1}^{3} (h_\theta(x^{(i)}) - y^{(i)})^2 = 0^2 + 10^2 + 0^2 = 100$

步骤4：计算代价函数 $J(\theta_0, \theta_1) = \frac{1}{2 \times 3} \times 100 = \frac{100}{6} \approx 16.67$

所以代价函数值约为 16.67。这个值越小，说明模型的预测越准确。

对于线性回归，偏导数为：

• $\frac{\partial J}{\partial \theta_0} = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})$
• $\frac{\partial J}{\partial \theta_1} = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x^{(i)}$

步骤1：计算预测误差（已在上题计算过）

• 误差1：$e^{(1)} = 150 - 150 = 0$
• 误差2：$e^{(2)} = 210 - 200 = 10$
• 误差3：$e^{(3)} = 250 - 250 = 0$

步骤2：计算 $\theta_0$ 的梯度 $\frac{\partial J}{\partial \theta_0} = \frac{1}{3}(0 + 10 + 0) = \frac{10}{3} \approx 3.33$

步骤3：计算 $\theta_1$ 的梯度 $\frac{\partial J}{\partial \theta_1} = \frac{1}{3}(0 \times 50 + 10 \times 80 + 0 \times 100) = \frac{800}{3} \approx 266.67$

步骤4：更新参数 $\theta_0 := 50 - 0.01 \times 3.33 = 50 - 0.0333 = 49.967$ $\theta_1 := 2 - 0.01 \times 266.67 = 2 - 2.667 = -0.667$

更新后的参数为：$\theta_0 \approx 49.97$，$\theta_1 \approx -0.67$

注意：$\theta_1$ 变成了负数，这说明这次更新的步长可能过大（学习率0.01对这个问题来说偏大了），或者初始参数选择不当。在实际应用中，我们需要进行多次迭代，代价函数会逐渐收敛到最小值。你可以尝试用更小的学习率（如0.0001）重新计算，看看结果如何。