线性代数小回顾

当我们初次接触机器学习时，可能会对各种数学符号感到困惑。但如果仔细观察就会发现，机器学习中的很多操作本质上都是在处理数字的集合——数据集包含大量样本，每个样本可能有多个特征。如何高效地表示和处理这些数据？这就是线性代数发挥作用的地方。

线性代数为我们提供了一套简洁而强大的数学工具，让我们能够用统一的符号和运算来处理多维数据。想象一下，如果没有矩阵，我们要处理一个包含一千个样本、每个样本一百个特征的数据集，需要写多少个方程？但用矩阵表示，只需要一个简单的矩阵乘法。

在这一个部分中，我们将回顾线性代数的核心概念和运算。这些内容可能你在之前的数学课程中学过，但现在我们要从机器学习的角度重新理解它们。我们不会追求数学的严格性和完备性，而是聚焦于机器学习中最常用的部分，强调直观理解和实际应用。

矩阵与向量：数据的数学表达

在开始运算之前，我们首先要理解矩阵和向量是什么，它们在机器学习中代表什么。

向量可以看作是数字的有序列表。比如一个房子的特征——面积80平方米、有3个卧室、房龄5年——可以表示为向量 $[80, 3, 5]$。在数学上，我们通常把向量写成列的形式：

$\mathbf{v} = \begin{bmatrix} 80 \\ 3 \\ 5 \end{bmatrix}$

这个向量有3个元素（或称为3维），我们说它是一个 $3 \times 1$ 的向量（3行1列）。向量的每个元素对应一个特征的值。

矩阵是向量的推广，它是数字的二维数组。如果我们有4套房子，每套房子用一个向量表示，把这4个向量组合起来就得到一个矩阵：

这是一个 $4 \times 3$ 的矩阵（4行3列）。每一行代表一个样本（一套房子），每一列代表一个特征（面积、卧室数、房龄）。这种用矩阵表示数据集的方式在机器学习中无处不在。

我们用 $A_{ij}$ 或 $A[i,j]$ 表示矩阵 $A$ 的第 $i$ 行第 $j$ 列的元素。注意索引通常从1开始（数学约定），但在编程中常从0开始。在上面的矩阵 中，，表示第2个房子的第3个特征（房龄）是8年。

向量可以看作是特殊的矩阵——只有一列的矩阵（列向量）或只有一行的矩阵（行向量）。在机器学习中，我们默认向量是列向量。行向量写作 $\mathbf{v}^T$，表示列向量 $\mathbf{v}$ 的转置。

矩阵和向量不仅是数据的容器，它们还承载着几何意义。一个二维向量可以看作平面上的一个点或一个从原点出发的箭头。一个三维向量则对应三维空间中的点或箭头。虽然我们无法可视化高维向量，但这种几何直觉仍然有用——高维向量仍然代表"空间"中的位置或方向。

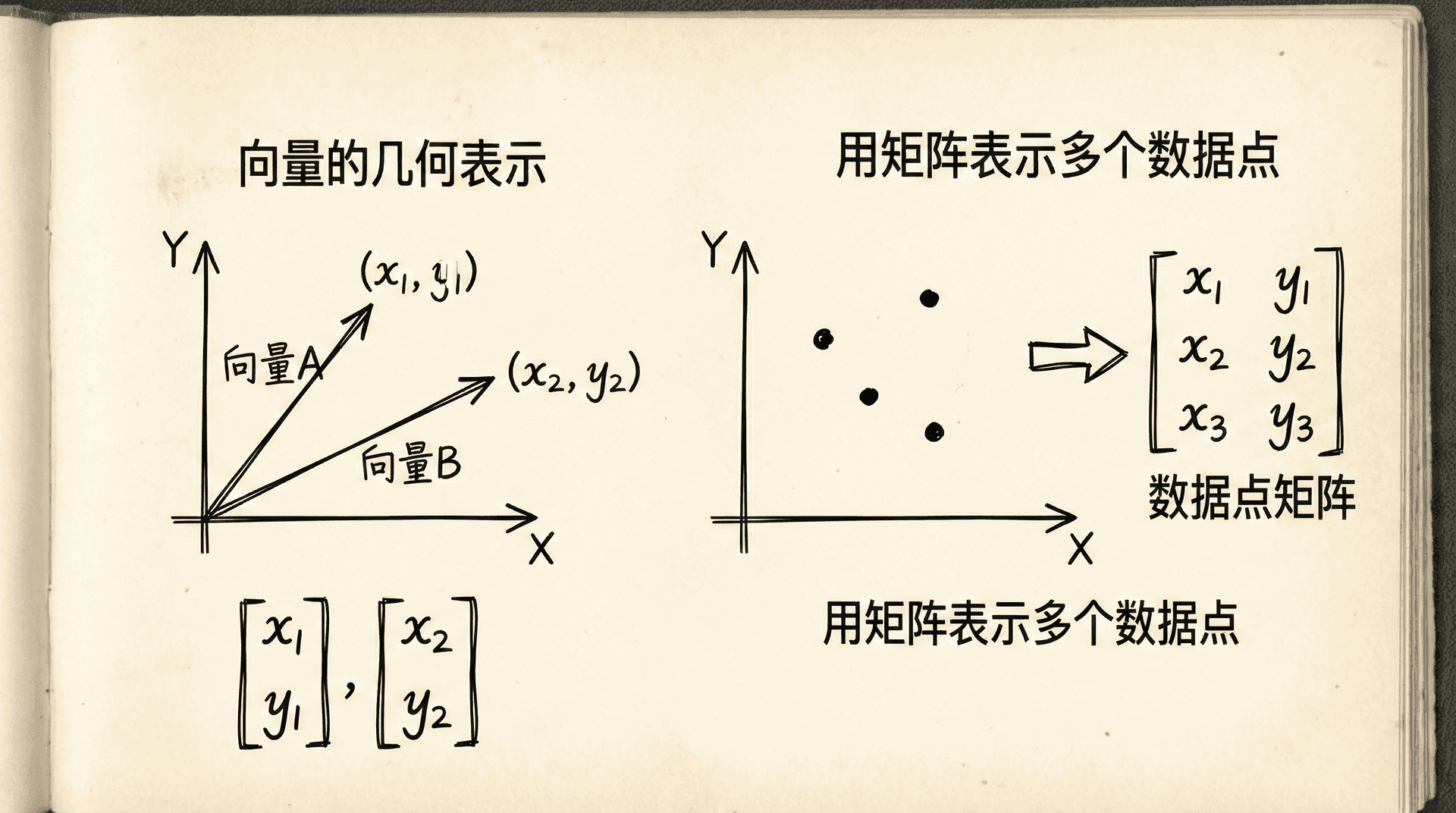
矩阵也有几何解释。矩阵可以看作是一个线性变换，它把一个向量映射到另一个向量。比如旋转、缩放、投影等几何变换都可以用矩阵表示。这种视角在理解机器学习算法时会很有帮助。

基本运算：加法与标量乘法

现在让我们看看如何对矩阵和向量进行运算。最简单的运算是加法和标量乘法。

矩阵加法：两个相同尺寸的矩阵可以相加，结果是对应元素相加。如果：

$A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad B = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}$

那么：

$A + B = \begin{bmatrix} 1+5 & 2+6 \\ 3+7 & 4+8 \end{bmatrix} = \begin{bmatrix} 6 & 8 \\ 10 & 12 \end{bmatrix}$

矩阵加法满足交换律和结合律，就像普通数字的加法一样：$A + B = B + A$，$(A + B) + C = A + (B + C)$。

标量乘法：一个标量（普通数字）乘以矩阵，等于这个数乘以矩阵的每个元素。如果 $c = 3$，那么：

$cA = 3 \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} 3 & 6 \\ 9 & 12 \end{bmatrix}$

向量的加法和标量乘法与矩阵完全类似。两个向量相加，对应元素相加：

$\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} + \begin{bmatrix} 4 \\ 5 \\ 6 \end{bmatrix} = \begin{bmatrix} 5 \\ 7 \\ 9 \end{bmatrix}$

标量乘以向量，每个元素都乘以这个标量：

$2 \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} = \begin{bmatrix} 2 \\ 4 \\ 6 \end{bmatrix}$

这些运算看起来简单，但它们在机器学习中有重要应用。比如，在梯度下降中，我们需要计算 $\theta := \theta - \alpha \nabla J$，这里就涉及标量乘法（$\alpha$ 乘以梯度向量）和向量减法（$\theta$ 减去结果）。

在实际计算中，我们经常会对整个数据集进行统一的操作。比如，如果我们想把所有房价都转换成以千元为单位（原来是以万元为单位），只需要把价格向量乘以10。如果我们想给所有特征加上一个偏移量，只需要做向量加法。矩阵运算让这些批量操作变得简单直接。

|
import numpy as np
 
# 矩阵加法示例
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
C = A + B
print("A + B =")
print(C)
 
# 标量乘法示例
scalar =

|
A + B =
[[ 6  8]
 [10 12]]
 
3 * A =
[[ 3  6]
 [ 9 12]]
 
v1 + v2 = [5 7 9]

矩阵与向量的乘法

矩阵乘法是线性代数中最重要也最强大的运算。它在机器学习中无处不在，理解它是理解算法的关键。

首先看矩阵与向量的乘法。设 $A$ 是一个 $m \times n$ 的矩阵，$\mathbf{x}$ 是一个 $n \times 1$ 的向量，它们的乘积 $A\mathbf{x}$ 是一个 $m \times 1$ 的向量。计算规则是：结果向量的第 个元素等于 的第 行与 的点积（对应元素相乘再相加）。

举个具体例子：

$\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \begin{bmatrix} 7 \\ 8 \\ 9 \end{bmatrix} = \begin{bmatrix} 1 \times 7 + 2 \times 8 + 3 \times 9 \\ 4 \times 7 + 5 \times 8 + 6 \times 9 \end{bmatrix} = \begin{bmatrix} 50 \\ 122 \end{bmatrix}$

为什么要这样定义乘法？让我们从线性回归的角度理解。回忆线性回归的假设函数：

$h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + ... + \theta_n x_n$

如果我们把参数写成向量 $\boldsymbol{\theta} = [\theta_0, \theta_1, ..., \theta_n]^T$，特征写成向量 （注意我们加了 ），那么假设函数可以简洁地写成：

$h_\theta(x) = \boldsymbol{\theta}^T \mathbf{x}$

这就是向量的点积（或内积）！现在如果我们有多个样本，把所有样本的特征向量作为矩阵 $X$ 的行，那么所有样本的预测值可以一次性计算出来：

$\mathbf{h} = X\boldsymbol{\theta}$

这就是矩阵向量乘法的威力——用一个简洁的表达式就能表示对整个数据集的预测。

让我们看一个完整的例子。假设我们有3个房子，每个房子有2个特征（面积和房龄），参数为 $\theta_0 = 10$，$\theta_1 = 2$，$\theta_2 = -0.5$：

$X = \begin{bmatrix} 1 & 80 & 5 \\ 1 & 95 & 8 \\ 1 & 70 & 3 \end{bmatrix}, \quad \boldsymbol{\theta} = \begin{bmatrix} 10 \\ 2 \\ -0.5 \end{bmatrix}$

那么预测值是：

$X\boldsymbol{\theta} = \begin{bmatrix} 1 & 80 & 5 \\ 1 & 95 & 8 \\ 1 & 70 & 3 \end{bmatrix} \begin{bmatrix} 10 \\ 2 \\ -0.5 \end{bmatrix} = \begin{bmatrix} 10 + 160 - 2.5 \\ 10 + 190 - 4 \\ 10 + 140 - 1.5 \end{bmatrix} = \begin{bmatrix} 167.5 \\ 196 \\ 148.5 \end{bmatrix}$

三个房子的预测价格分别是167.5万、196万、148.5万。只用一行代码 predictions = X.dot(theta) 就能完成所有计算，这比写循环要优雅和高效得多。

从几何角度看，矩阵向量乘法可以理解为一个变换：它把一个向量变换到另一个向量。比如，$A\mathbf{x}$ 把向量 $\mathbf{x}$ 变换为新的向量 $A\mathbf{x}$。这个变换可能是旋转、缩放、投影等几何操作的组合。

矩阵与矩阵的乘法

理解了矩阵向量乘法，矩阵矩阵乘法就很自然了。如果 $A$ 是 $m \times n$ 矩阵，$B$ 是 $n \times p$ 矩阵，它们的乘积 $AB$ 是 $m \times p$ 矩阵。

计算方法是：$AB$ 的第 $i$ 行第 $j$ 列的元素，等于 $A$ 的第 $i$ 行与 $B$ 的第 $j$ 列的点积。换句话说，我们把 $B$ 的每一列看作一个向量，分别与 相乘（矩阵向量乘法），得到的结果向量组成 的各列。

举例：

$\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} = \begin{bmatrix} 1 \times 5 + 2 \times 7 & 1 \times 6 + 2 \times 8 \\ 3 \times 5 + 4 \times 7 & 3 \times 6 + 4 \times 8 \end{bmatrix} = \begin{bmatrix} 19 & 22 \\ 43 & 50 \end{bmatrix}$

矩阵乘法满足结合律：$(AB)C = A(BC)$，但不满足交换律：$AB \neq BA$（事实上，很多时候 $AB$ 和 $BA$ 的维度都不匹配，无法相乘）。这是矩阵乘法与普通数字乘法的重要区别。

矩阵乘法在机器学习中有广泛应用。在神经网络中，每一层的计算都是矩阵乘法：输入矩阵乘以权重矩阵，得到下一层的输入。在数据预处理中，我们可能需要对数据进行线性变换，这也是通过矩阵乘法实现的。

让我们看一个实际例子。假设我们想对特征做标准化处理（减去均值，除以标准差）。如果有3个样本，2个特征：

$X = \begin{bmatrix} 80 & 5 \\ 95 & 8 \\ 70 & 3 \end{bmatrix}$

我们可以构造一个变换矩阵来实现标准化。虽然通常我们用向量化的减法和除法，但原理上可以用矩阵乘法来表示线性变换。

矩阵乘法的计算复杂度是需要注意的。两个 $n \times n$ 矩阵相乘，朴素算法需要 $O(n^3)$ 次乘法运算。当 $n$ 很大时，这是一个巨大的计算量。现代的线性代数库（如NumPy、MATLAB）使用了高度优化的算法和硬件加速（如GPU），可以快速完成大规模矩阵运算。

|
# 矩阵乘法示例
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
 
# 使用 dot 方法或 @ 运算符
C = A.dot(B)  # 或者 C = A @ B
print("A * B =")
print(C)
 
# 验证维度规则
A = np.array([[1, 

|
A * B =
[[19 22]
 [43 50]]
 
(2x3) * (3x2) =
[[ 58  64]
 [139 154]]
结果的形状: (2, 2)

矩阵乘法的性质与应用

矩阵乘法虽然不满足交换律，但有很多其他有用的性质。

单位矩阵 $I$ 是对角线上全是1、其他位置全是0的方阵：

$I = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$

单位矩阵的特殊之处在于，任何矩阵乘以单位矩阵都等于它自己：$AI = IA = A$（当然要求维度匹配）。单位矩阵就像数字乘法中的1。

矩阵乘法满足分配律：$A(B + C) = AB + AC$，$(A + B)C = AC + BC$。这意味着矩阵乘法可以"展开"，就像代数中的乘法分配律。

矩阵乘法的结合律 $(AB)C = A(BC)$ 意味着多个矩阵相乘时，我们可以选择任意的计算顺序。但不同的顺序可能导致不同的计算复杂度。比如计算 $ABC$，如果先算 $AB$ 再乘 $C$，可能比先算 $BC$ 再让 去乘结果要快或慢，这取决于矩阵的尺寸。

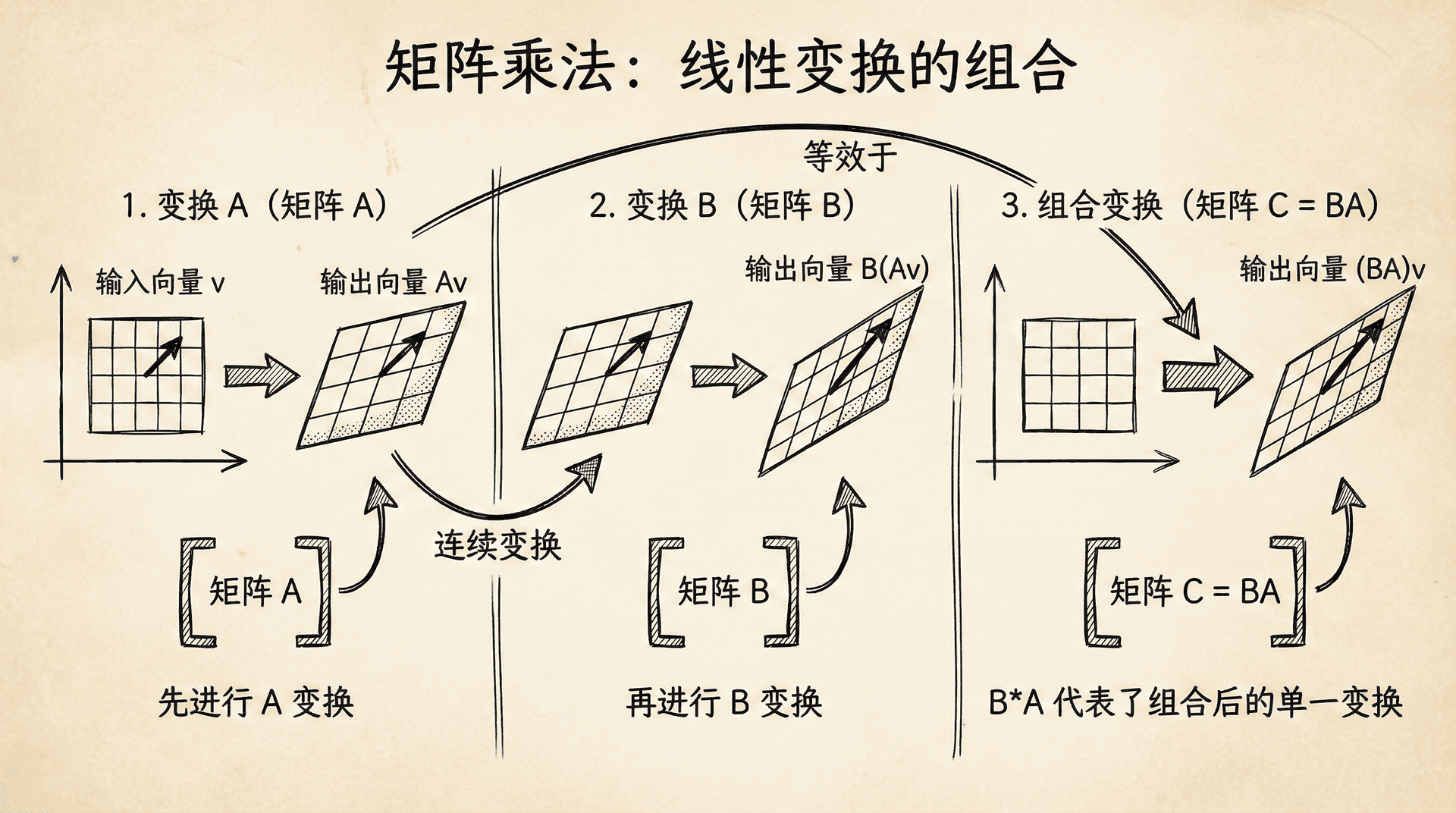
在机器学习中，矩阵乘法让我们能够简洁地表达复杂的计算。比如，在计算代价函数时，我们需要计算 $(X\theta - y)^T(X\theta - y)$。这个表达式用标量表示会非常冗长，但用矩阵表示既简洁又能高效计算。

再比如，在神经网络的前向传播中，如果第一层有100个神经元，第二层有50个神经元，第一层到第二层的权重就是一个 $50 \times 100$ 的矩阵 $W$。如果输入是一个批次的32个样本（$32 \times 100$ 的矩阵 $X$），那么第二层的激活值（在应用激活函数前）就是 $XW^T$，一个 的矩阵。一次矩阵乘法就完成了整个批次在这一层的计算。

矩阵乘法还能表示数据的线性组合。比如，如果 $A$ 是数据矩阵，$W$ 是权重矩阵，$AW$ 的每一列都是 $A$ 的列的加权组合，权重由 $W$ 的相应列给出。这在降维、特征提取等任务中非常有用。

逆矩阵与转置

在普通数字中，除了加减乘，我们还有除法（或者说乘以倒数）。在矩阵世界中，"除法"对应的概念是矩阵的逆。

对于方阵 $A$（行数和列数相等的矩阵），如果存在矩阵 $A^{-1}$ 使得：

$AA^{-1} = A^{-1}A = I$

那么我们称 $A^{-1}$ 是 $A$ 的逆矩阵。逆矩阵就像倒数，$A$ 乘以它的逆得到单位矩阵，就像一个数乘以它的倒数得到1。

但不是所有矩阵都有逆矩阵。如果一个矩阵有逆，我们称它是可逆的或非奇异的；否则称它是奇异的。什么样的矩阵没有逆？直观地说，如果一个矩阵对应的线性变换"压缩"了空间（比如把三维空间压成一个平面），那它就没有逆——因为我们无法从压缩后的结果恢复原始信息。

在机器学习中，矩阵的逆出现在很多地方。最典型的是线性回归的正规方程（Normal Equation）：

$\theta = (X^TX)^{-1}X^Ty$

这个公式直接给出了线性回归的最优参数，不需要迭代。但它要求 $X^TX$ 是可逆的。如果特征之间存在线性相关性，或者特征数多于样本数，$X^TX$ 可能不可逆，这时候正规方程就无法使用，我们需要用梯度下降或者正则化技术。

计算矩阵的逆在计算上是昂贵的，对于 $n \times n$ 矩阵，复杂度是 $O(n^3)$。而且数值计算中，矩阵求逆可能带来数值不稳定问题。因此在实际应用中，我们尽量避免显式地计算矩阵的逆，而是用其他数值方法（如LU分解、Cholesky分解）来解线性方程组。

转置是另一个重要的矩阵运算。矩阵 $A$ 的转置 $A^T$ 是把 $A$ 的行和列互换：$A^T$ 的第 $i$ 行第 $j$ 列元素等于 的第 行第 列元素。

$\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}^T = \begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{bmatrix}$

转置有一些好用的性质：

• $(A^T)^T = A$（转置两次回到原来）
• $(A + B)^T = A^T + B^T$（和的转置等于转置的和）

在机器学习中，转置经常用于调整矩阵的形状以便进行运算。比如，如果 $\mathbf{x}$ 是列向量，$\mathbf{x}^T\mathbf{x}$ 是向量的范数平方（所有元素平方之和），而 $\mathbf{x}\mathbf{x}^T$ 是一个方阵（外积）。这两个运算在不同的场景下都很有用。

|
# 转置示例
A = np.array([[1, 2, 3], [4, 5, 6]])
A_T = A.T
print("原矩阵:")
print(A)
print("\n转置后:")
print(A_T)
 
# 逆矩阵示例
B = np.array([[1, 

线性代数在机器学习中的应用

现在让我们把这些概念串起来，看看线性代数如何简化机器学习的表达和计算。

回到线性回归。假设我们有 $m$ 个样本，$n$ 个特征。数据矩阵 $X$ 是 $m \times (n+1)$（多了一列全是1，对应 $x_0$），参数向量 是 ，标签向量 是 。

预测值：$\mathbf{h} = X\theta$（一个矩阵向量乘法）

误差向量：$\mathbf{e} = X\theta - y$（一个向量减法）

代价函数：$J(\theta) = \frac{1}{2m} \mathbf{e}^T\mathbf{e}$（向量的范数平方）

梯度：$\nabla J = \frac{1}{m} X^T\mathbf{e} = \frac{1}{m} X^T(X\theta - y)$（矩阵向量乘法）

参数更新：$\theta := \theta - \alpha \nabla J$（向量减法和标量乘法）

看，整个梯度下降算法可以用几行简洁的矩阵运算表达！而且这些运算可以直接翻译成代码，高效执行。

|
# 向量化的线性回归梯度下降
def gradientDescentVectorized(X, y, theta, alpha, numIter):
    m = len(y)
    for i in range(numIter):
        # 预测值
        h = X @ theta
        # 误差
        error = h - y
        # 梯度
        gradient = (1/m) * (X.T @ error)
        # 更新参数
        theta 

这个实现只有几行代码，但它能处理任意数量的样本和特征。对比用循环写的版本，向量化的代码不仅更简洁，执行速度也快得多。

在更高级的算法中，线性代数的作用更加明显。主成分分析（PCA）的核心是计算协方差矩阵的特征值和特征向量。支持向量机（SVM）涉及二次规划，需要解一个线性方程组。神经网络的每一层都是矩阵乘法和元素级的非线性函数。深度学习框架（如TensorFlow、PyTorch）的核心就是高效的张量（高维矩阵）运算。

线性代数还为我们提供了分析算法的工具。比如，通过分析某个矩阵的秩，我们可以判断特征是否线性相关。通过分析矩阵的条件数，我们可以判断数值计算的稳定性。通过矩阵分解（如SVD、QR分解），我们可以揭示数据的内在结构。

从计算工具到思维方式

学习线性代数，我们不仅获得了一套计算工具，更重要的是获得了一种思维方式。线性代数教会我们用向量和矩阵来思考问题，用线性变换来理解算法，用几何直觉来解释公式。

当我们看到机器学习算法时，不要被复杂的公式吓倒。试着把它翻译成矩阵语言，你会发现很多看似复杂的操作实际上就是几个基本的矩阵运算的组合。试着从几何角度理解它，你会对算法的本质有更深的认识。

在接下来的课程中，我们会频繁使用线性代数的符号和概念。每当你遇到矩阵运算时，不妨想一想：这个运算代表什么？为什么要这样运算？有没有更简洁的表达方式？这种思考会加深你对算法的理解。

在下一节课中，我们将把线性回归扩展到多元情况，处理具有多个特征的数据。你会看到，有了线性代数的语言，多元线性回归和单变量线性回归在形式上几乎没有区别——公式是一样的，只不过标量变成了向量，变量变成了矩阵。

小练习

1. 矩阵乘法与数据表示：假设我们有一个数据矩阵 $X$，包含3个样本，每个样本有2个特征（面积和房龄）：

   $X = \begin{bmatrix} 1 & 80 & 5 \\ 1 & 100 & 8 \\ 1 & 65 & 3 \end{bmatrix}$

2. 矩阵转置与梯度计算：在机器学习中，我们经常需要计算 $X^T X$ 和 $X^T y$。给定：

   $X=\left[\begin{array}{cc}1& 2\\ 1& 3\\ 1& 4\end{array}\right],y=[\begin{array}{c}5\\ \end{array}$

参数向量为：

$\theta = \begin{bmatrix} 50 \\ 2 \\ -3 \end{bmatrix}$

计算 $X\theta$ 的结果，并解释它在线性回归中的含义。

步骤2：计算第二行 $X_{2:} \cdot \theta = 1 \times 50 + 100 \times 2 + 8 \times (-3) = 50 + 200 - 24 = 226$

步骤3：计算第三行 $X_{3:} \cdot \theta = 1 \times 50 + 65 \times 2 + 3 \times (-3) = 50 + 130 - 9 = 171$

最终结果： $X\theta = \begin{bmatrix} 195 \\ 226 \\ 171 \end{bmatrix}$

在线性回归中的含义：

• $X$ 的每一行代表一个样本，第一列是偏置项（总是1），第二列是面积特征，第三列是房龄特征
• $\theta$ 是模型参数：$\theta_0 = 50$（截距），$\theta_1 = 2$（面积的权重），$\theta_2 = -3$（房龄的权重）
• $X\theta$ 的结果是模型对3个样本的预测值，分别是195万元、226万元和171万元
• 这个矩阵乘法实际上是向量化地计算了 $h_\theta(x^{(i)}) = \theta_0 + \theta_1 x_1^{(i)} + \theta_2 x_2^{(i)}$
• 用一次矩阵乘法替代了3次循环计算，这就是向量化的威力！

计算 $X^T X$ 和 $X^T y$ 的值。

步骤2：计算 $X^T X$

$X^T$ 是 $2 \times 3$，$X$ 是 $3 \times 2$，所以 $X^T X$ 是 $2 \times 2$ 矩阵：

$X^T X = \begin{bmatrix} 1 & 1 & 1 \\ 2 & 3 & 4 \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 1 & 3 \\ 1 & 4 \end{bmatrix}$

计算每个元素：

• $(X^T X)_{11} = 1 \times 1 + 1 \times 1 + 1 \times 1 = 3$
• $(X^T X)_{12} = 1 \times 2 + 1 \times 3 + 1 \times 4 = 9$
• $(X^T X)_{21} = 2 \times 1 + 3 \times 1 + 4 \times 1 = 9$
• $(X^T X)_{22} = 2 \times 2 + 3 \times 3 + 4 \times 4 = 4 + 9 + 16 = 29$

$X^T X = \begin{bmatrix} 3 & 9 \\ 9 & 29 \end{bmatrix}$

步骤3：计算 $X^T y$

$X^T$ 是 $2 \times 3$，$y$ 是 $3 \times 1$，所以 $X^T y$ 是 $2 \times 1$ 向量：

$X^T y = \begin{bmatrix} 1 & 1 & 1 \\ 2 & 3 & 4 \end{bmatrix} \begin{bmatrix} 5 \\ 7 \\ 9 \end{bmatrix}$

计算每个元素：

• $(X^T y)_1 = 1 \times 5 + 1 \times 7 + 1 \times 9 = 21$
• $(X^T y)_2 = 2 \times 5 + 3 \times 7 + 4 \times 9 = 10 + 21 + 36 = 67$

$X^T y = \begin{bmatrix} 21 \\ 67 \end{bmatrix}$

在机器学习中的应用：

• 这两个计算是正规方程 $\theta = (X^T X)^{-1} X^T y$ 的核心部分
• $X^T X$ 是一个对称矩阵，它衡量了特征之间的相关性
• $X^T y$ 衡量了特征与目标变量之间的相关性
• 在Python中，这些计算可以写成：X.T @ X 和 X.T @ y，非常简洁！