机器学习系统设计

我们已经学习了多种机器学习算法——线性回归、逻辑回归、神经网络。我们知道如何训练模型，如何计算梯度，如何优化参数。但在实际应用中，仅仅知道这些算法是不够的。我们还需要知道如何评估模型、诊断问题、改进性能。

当你的模型表现不佳时，有很多可能的改进方向：获取更多训练数据、增加或减少特征、调整正则化参数、改变网络架构……面对这么多选择，如何决定下一步该做什么？如果盲目尝试，可能会浪费大量时间在无用的方向上。

这一节我们将学习系统化的方法来评估和改进机器学习模型。我们会学习如何划分数据集、如何诊断偏差和方差问题、如何使用学习曲线指导优化。

决定下一步做什么

假设你已经实现了正则化线性回归来预测房价，但在测试集上表现不好——误差很大。你会怎么做？可能的选择包括：

• 获取更多的训练数据
• 尝试更少的特征（特征选择）
• 尝试更多的特征（如增加多项式特征）
• 增加正则化参数 $\lambda$
• 减小正则化参数 $\lambda$
• 改用更复杂的模型（如神经网络）
• 改用更简单的模型

哪个选择是对的？不同的问题需要不同的解决方案。如果模型是欠拟合（高偏差），获取更多数据不会有太大帮助；如果是过拟合（高方差），增加特征会让情况更糟。

关键是要先诊断问题，然后针对性地解决。这就需要系统化的评估方法。

评估假设：训练集误差不够

在前面的学习中，我们一直用训练集的代价函数 $J(\theta)$ 来评估模型。但这是不够的！训练误差只告诉我们模型在“见过”的数据上表现如何，不能反映模型在“没见过”的新数据上的性能。

一个过拟合的模型在训练集上表现完美（误差接近0），但在新数据上表现很差。这就像一个学生死记硬背练习题答案，考试遇到原题就能答对，但遇到新题就不会做。

解决方法是留出一部分数据作为测试集（Test Set）：

1. 将数据随机分成训练集和测试集，常见比例是70%-80%用于训练，20%-30%用于测试
2. 只用训练集训练模型
3. 用测试集评估模型性能

对于线性回归，测试集误差是：

$J_{test}(\theta) = \frac{1}{2m_{test}} \sum_{i=1}^{m_{test}} (h_\theta(x_{test}^{(i)}) - y_{test}^{(i)})^2$

对于分类问题，除了代价函数，还可以用分类错误率（Misclassification Error）：

$\text{Test Error} = \frac{1}{m_{test}} \sum_{i=1}^{m_{test}} \text{err}(h_\theta(x_{test}^{(i)}), y_{test}^{(i)})$

其中 $\text{err}(h_\theta(x), y) = 1$ 如果预测错误，否则为0。

|
from sklearn.model_selection import train_test_split
 
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)
 
# 训练模型
theta = train(X_train, y_train)
 
# 评估
train_error = computeError(X_train, y_train, theta)
test_error = computeError(X_test, y_test, theta)
 
print(f"训练误差: {train_error:.4f}

关键洞察：

• 如果训练误差低但测试误差高，模型过拟合了
• 如果训练误差和测试误差都高，模型欠拟合了
• 如果训练误差和测试误差都低且接近，模型表现良好

模型选择：验证集的引入

假设我们要决定多项式的次数——用1次、2次还是10次多项式？我们可以尝试每个选择，在测试集上评估，选择测试误差最小的那个。

但这有一个问题：我们用测试集来选择模型，相当于把测试集当作训练过程的一部分。选出的模型已经"看过"测试集了，在这个测试集上的误差会偏低，不能准确反映在真实新数据上的表现。

解决方法是引入第三个数据集——验证集（Validation Set，也叫开发集Dev Set）：

数据划分为三部分：

• 训练集（60%）：用于训练模型参数
• 验证集（20%）：用于选择模型（超参数、架构等）
• 测试集（20%）：用于最终评估性能，只用一次

模型选择流程：

1. 用训练集训练不同的候选模型（比如1-10次多项式）
2. 在验证集上评估每个模型，记录 $J_{cv}(\theta)$（cv代表cross-validation）
3. 选择验证误差最小的模型
4. 用测试集评估选出的模型，得到对真实性能的无偏估计

|
# 尝试不同的多项式次数
degrees = range(1, 11)
train_errors = []
val_errors = []
 
for d in degrees:
    # 构造多项式特征
    X_poly_train = polyFeatures(X_train, d)
    X_poly_val = polyFeatures(X_val, d)
    
    # 训练
    theta = train(X_poly_train, y_train)
    
    # 评估
    train_errors.append(computeError(X_poly_train, y_train, theta))
    val_errors.append(computeError(X_poly_val, y_val, theta))

诊断偏差与方差

理解模型的问题是高偏差（欠拟合）还是高方差（过拟合）非常重要，因为它们需要完全不同的解决方法。

• 偏差（Bias）：模型对数据的假设过于简单，无法捕捉数据的真实规律。高偏差导致欠拟合，训练误差和验证误差都很高。
• 方差（Variance）：模型对训练数据的细节过于敏感，学到了噪声而不是规律。高方差导致过拟合，训练误差很低但验证误差很高。

如何诊断？看训练误差和验证误差的关系：

画出学习曲线可以更清楚地看到问题：

|
import matplotlib.pyplot as plt
 
plt.figure(figsize=(10, 6))
plt.plot(degrees, train_errors, 'o-', label='训练误差')
plt.plot(degrees, val_errors, 'o-', label='验证误差')
plt.xlabel('多项式次数')
plt.ylabel('误差')
plt.legend()
plt.title('训练误差 vs 验证误差')
plt.show()

典型的曲线形状：

• 左边（低复杂度）：训练误差和验证误差都高，两者接近——高偏差
• 中间（适当复杂度）：训练误差和验证误差都低且接近——最优点
• 右边（高复杂度）：训练误差很低，验证误差很高——高方差

正则化与偏差-方差权衡

正则化参数 $\lambda$ 直接影响偏差和方差：

• $\lambda$ 很大：权重被强制接近0，模型变简单，高偏差，欠拟合
• $\lambda$ 很小：正则化作用弱，模型可能过于复杂，高方差，过拟合
• $\lambda$ 适中：在偏差和方差之间取得平衡

选择最优 $\lambda$ 的方法：

1. 尝试一系列 $\lambda$ 值：0, 0.01, 0.02, 0.04, 0.08, 0.16, ..., 10
2. 对每个 $\lambda$，在训练集上训练模型
3. 在验证集上评估，选择验证误差最小的 $\lambda$
4. 用测试集评估最终性能

|
lambda_values = [0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]
train_errors = []
val_errors = []
 
for lam in lambda_values:
    theta = trainWithRegularization(X_train, y_train, lam)
    train_errors.append(computeError(X_train, y_train, theta))
    val_errors.append(computeError(X_val, y_val, theta))
 

学习曲线

学习曲线（Learning Curve）画出训练误差和验证误差随训练样本数量的变化。它能帮助我们理解：

• 模型是否从更多数据中受益
• 当前的瓶颈是什么

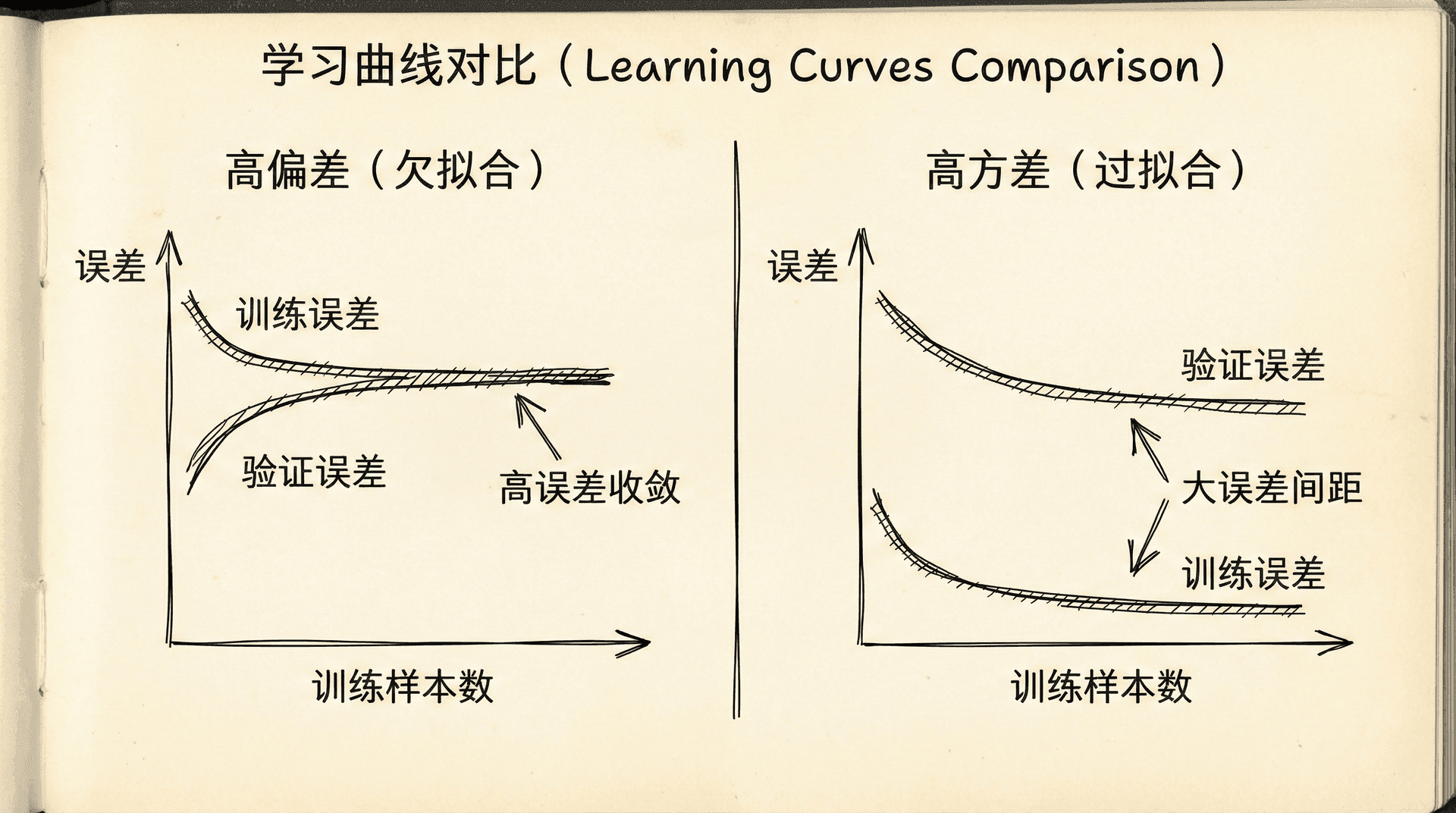
高偏差的学习曲线：

• 训练误差和验证误差都很高
• 两条曲线很快收敛到一个高水平
• 结论：增加更多训练数据不会有太大帮助，需要更复杂的模型

高方差的学习曲线：

• 训练误差很低
• 验证误差远高于训练误差
• 两条曲线之间有很大的gap
• 随着数据增加，gap可能会缩小
• 结论：获取更多数据可能有帮助

|
def plotLearningCurve(X, y, X_val, y_val):
    """绘制学习曲线"""
    m = X.shape[0]
    train_errors = []
    val_errors = []
    
    # 逐步增加训练样本
    for i in range(1, m + 1):
        theta = train(X[:i], y[:i])
        train_errors.append(computeError(X[:i], y[:i], theta))
        val_errors.append(computeError(X_val, y_val, theta))
    
    plt.plot(range(

决定接下来做什么的系统化方法

现在我们有了完整的工具箱来诊断和改进模型。回到最初的问题：当模型表现不佳时该怎么办？

这个系统化的流程能够避免盲目尝试，节省大量时间。当然，经验也很重要——随着实践的积累，你会对不同问题应该用什么策略有更好的直觉。

在下一个部分中，我们将学习更多实践中的技巧——如何进行误差分析，如何处理不平衡数据，如何决定是否需要更多数据。这些技能会让你成为更高效的机器学习实践者。

小练习

1. 问题诊断和解决方案：根据以下情况，诊断问题并提出解决方案。

   你训练了一个模型，得到：

   • 训练误差：5%
   • 验证误差：25%

   这是什么问题？应该如何解决？

|
def diagnose_model(train_error, val_error):
    gap = val_error - train_error
    
    if train_error > 0.15:  # 高偏差
        if gap < 0.05:
            return "欠拟合（高偏差）"
        else:

2. 学习曲线分析：分析以下学习曲线，判断问题类型。

   随着训练样本数量增加：

   • 训练误差：从10%缓慢上升到18%
   • 验证误差：从60%缓慢下降到20%
   • 两条曲线在20%附近趋于平缓，但仍有差距

   这是什么问题？解决方案是什么？

|
高方差（过拟合）：
  训练误差：很低且平
  验证误差：高且有大gap
  解决：更多数据有帮助
  
高偏差（欠拟合）：
  训练误差：高且平
  验证误差：高且gap小
  解决：更多数据帮助不大，需要更复杂模型
  
理想状态：
  两条曲线都低且接近
  差距很小