神经网络学习

上个部分，我们学习了神经网络的结构和前向传播算法。我们知道了神经网络如何从输入计算输出，如何表示复杂的非线性函数。但一个关键问题还没有解决：如何确定网络中数以千计甚至百万计的权重参数？

手动设计权重只在最简单的情况下可行（如我们之前的AND/OR例子）。对于真实的应用——图像识别、语音识别、自然语言处理——网络可能有数百万个参数，手动设计是不可能的。我们需要让网络从数据中自动学习权重。

这一章我们将学习训练神经网络的核心算法——反向传播（Backpropagation）。这个算法让我们能够计算神经网络代价函数的梯度，从而使用梯度下降来优化权重。

神经网络的代价函数

在开始学习反向传播之前，我们需要定义神经网络的代价函数。它是逻辑回归代价函数的自然推广。

对于L层神经网络（L是总层数，包括输入层），设：

• $s_l$ 是第 $l$ 层的神经元数量（不包括偏置单元）
• $K$ 是输出层的神经元数量（类别数）
• $h_\Theta(x)_k$ 是输出的第 $k$ 个元素（第 $k$ 个类别的预测概率）

对于多分类问题，代价函数是：

$J(\Theta) = -\frac{1}{m} \sum_{i=1}^{m} \sum_{k=1}^{K} \left[ y_k^{(i)} \log(h_\Theta(x^{(i)})_k) + (1-y_k^{(i)}) \log(1-h_\Theta(x^{(i)})_k) \right] + \frac{\lambda}{2m} \sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}} (\Theta_{ji}^{(l)})^2$

让我们拆解这个看起来复杂的公式：

第一项是所有样本、所有输出单元的逻辑回归代价的总和。对于每个样本的每个输出，我们都计算一次逻辑回归代价。

第二项是正则化项，对所有层的所有权重（除了偏置项）进行L2正则化。注意我们对所有的 $\Theta_{ji}^{(l)}$ 求和，但通常不包括偏置项对应的权重（即 $j=0$ 的那一列）。

这个代价函数衡量的是：网络的预测与真实标签的差距（第一项），以及权重的大小（第二项）。我们的目标是找到使 $J(\Theta)$ 最小的权重。

反向传播算法

反向传播算法解决的核心问题是：如何计算代价函数对每个权重的偏导数 $\frac{\partial J}{\partial \Theta_{ij}^{(l)}}$？

对于逻辑回归，梯度的计算是直接的。但对于神经网络，输出依赖于多层的复杂计算，梯度的计算不那么明显。反向传播通过链式法则（Chain Rule）巧妙地解决了这个问题。

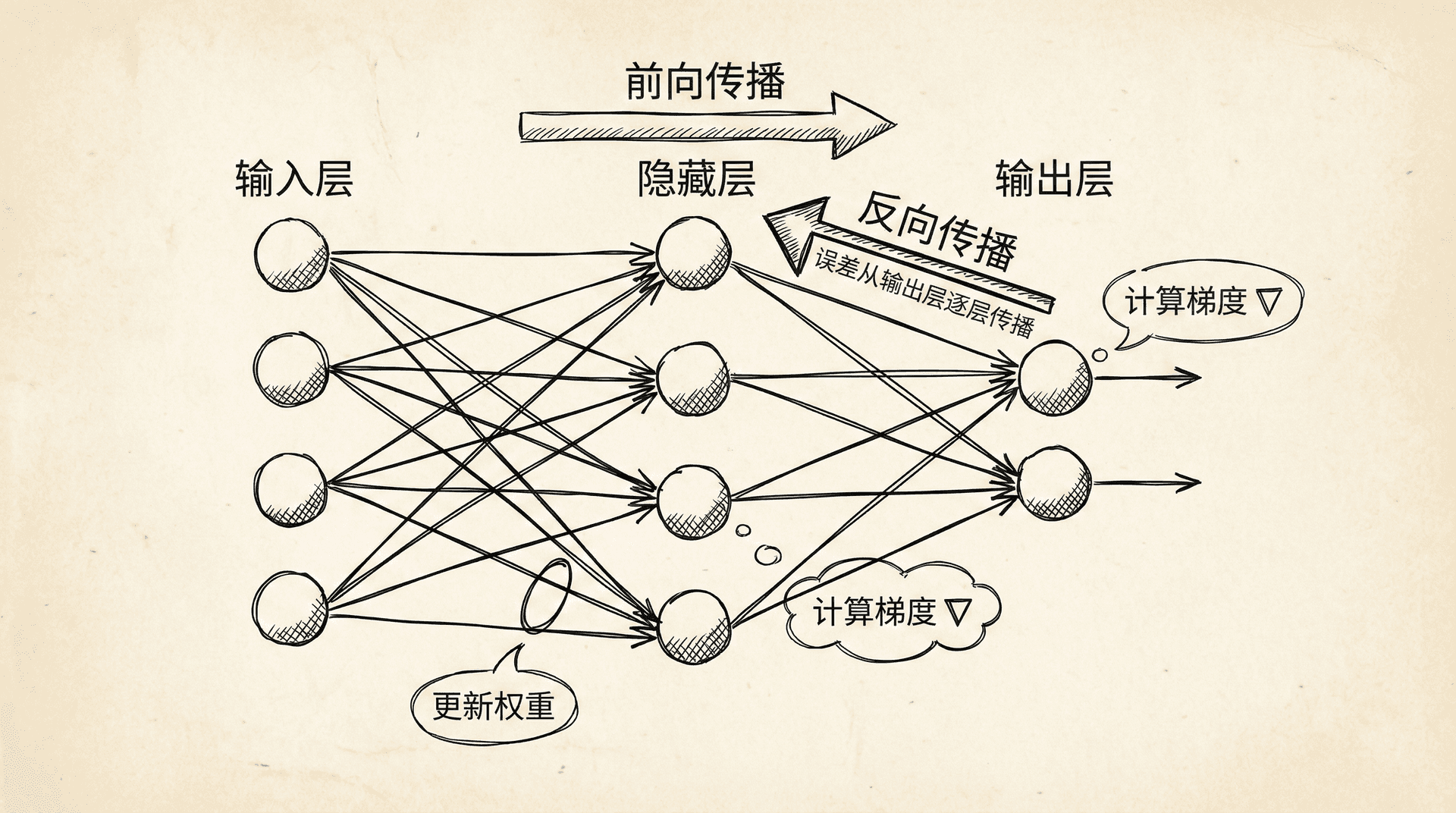
算法的名字“反向传播”来自于它的计算方式：误差从输出层开始，逐层向后传播到输入层。在传播过程中，我们计算每一层的误差，然后用这些误差计算梯度。

算法步骤：

完整算法（对于整个训练集）：

1. 初始化所有 $\Delta^{(l)} = 0$
2. 对于每个训练样本 $(x^{(i)}, y^{(i)})$：
   • 前向传播计算 $a^{(l)}$
   • 计算输出层误差 $\delta^{(L)}$
   • 反向传播计算 $\delta^{(l)}$
   • 累积 $\Delta^{(l)} := \Delta^{(l)} + \delta^{(l+1)} (a^{(l)})^T$
3. 计算梯度：$D^{(l)} = \frac{1}{m} \Delta^{(l)} + \frac{\lambda}{m} \Theta^{(l)}$（对于 $j \neq 0$）和 $D^{(l)} = \frac{1}{m} \Delta^{(l)}$（对于 $j = 0$）
4. 用梯度下降更新权重

理解反向传播

反向传播的数学推导涉及链式法则，比较复杂。但我们可以从直觉上理解它在做什么。

$\delta^{(l)}_j$ 可以理解为第 $l$ 层第 $j$ 个神经元的“误差”或“责任”——它对最终的代价函数贡献了多少误差。

• 输出层的误差很直观：就是预测值与真实值的差 $a^{(L)} - y$。如果预测太高，误差是正的；如果预测太低，误差是负的。
• 隐藏层的误差通过反向传播计算。一个隐藏层神经元的误差，取决于所有接收它输出的下一层神经元的误差，按照连接权重加权。换句话说，如果一个神经元对很多“有误差”的后续神经元有较大影响，那么它自己也应该承担较大的误差。

计算梯度时，我们用神经元的激活值乘以它的误差。这符合直觉：如果一个连接的输入激活值大，且输出有误差，那么这个连接的权重就需要较大的调整。

实现代码：

def backprop(X, y, Theta1, Theta2, lambda_reg):
    """
    反向传播算法
    X: 输入特征 (m x n)
    y: 标签 (m x K)，one-hot编码
    Theta1: 第一层权重
    Theta2: 第二层权重
    lambda_reg: 正则化参数
    """
    m = X.shape[0]
    
    # 初始化梯度累积器
    Delta1 = np.zeros_like(Theta1)
    Delta2 = np.zeros_like(Theta2)
    
    for i in range(m):
        # 前向传播
        a1 = X[i:i+1].T  # (n+1) x 1
        z2 = Theta1 @ a1
        a2 = sigmoid(z2)
        a2 = np.vstack([[[1]], a2])  # 添加偏置
        
        z3 = Theta2 @ a2
        a3 = sigmoid(z3)
        
        # 反向传播
        delta3 = a3 - y[i:i+1].T  # (K x 1)
        delta2 = (Theta2.T @ delta3) * (a2 * (1 - a2))
        delta2 = delta2[1:]  # 移除偏置单元的误差
        
        # 累积梯度
        Delta2 += delta3 @ a2.T
        Delta1 += delta2 @ a1.T
    
    # 计算最终梯度
    Theta1_grad = (1/m) * Delta1
    Theta2_grad = (1/m) * Delta2
    
    # 添加正则化（不包括偏置项）
    Theta1_grad[:, 1:] += (lambda_reg/m) * Theta1[:, 1:]
    Theta2_grad[:, 1:] += (lambda_reg/m) * Theta2[:, 1:]
    
    return Theta1_grad, Theta2_grad

展开参数与梯度检验

在实现反向传播时，参数通常组织成矩阵（$\Theta^{(1)}, \Theta^{(2)}, ...$）。但很多优化算法（如高级优化函数）需要参数是一个长向量。我们需要在矩阵表示和向量表示之间转换。

展开参数（Unrolling）：

# 将矩阵展开成向量
theta_vec = np.concatenate([Theta1.ravel(), Theta2.ravel()])
 
# 从向量恢复矩阵
Theta1 = theta_vec[:hidden_size * (input_size + 1)].reshape(hidden_size, input_size + 1)
Theta2 = theta_vec[hidden_size * (input_size + 1):].reshape(output_size, hidden_size + 1)

梯度检验（Gradient Checking）是验证反向传播实现正确性的重要技术。思想是用数值方法近似梯度，然后与反向传播计算的梯度比较。

数值梯度的计算：

$\frac{\partial J}{\partial \theta_i} \approx \frac{J(\theta + \epsilon e_i) - J(\theta - \epsilon e_i)}{2\epsilon}$

其中 $e_i$ 是第 $i$ 维为1其余为0的向量，$\epsilon$ 是一个小数（如 $10^{-4}$）。

def gradientCheck(X, y, Theta1, Theta2, lambda_reg, epsilon=1e-4):
    """
    数值梯度检验
    """
    # 用反向传播计算梯度
    Theta1_grad, Theta2_grad = backprop(X, y, Theta1, Theta2, lambda_reg)
    grad_backprop = np.concatenate([Theta1_grad.ravel(), Theta2_grad.ravel()])
    
    # 用数值方法计算梯度
    theta_vec = np.concatenate([Theta1.ravel(), Theta2.ravel()])
    grad_numerical = np.zeros_like(theta_vec)
    
    for i in range(len(theta_vec)):
        theta_plus = theta_vec.copy()
        theta_plus[i] += epsilon
        theta_minus = theta_vec.copy()
        theta_minus[i] -= epsilon
        
        # 计算代价函数（需要先恢复矩阵形式）
        J_plus = computeCost(X, y, unrollParameters(theta_plus), lambda_reg)
        J_minus = computeCost(X, y, unrollParameters(theta_minus), lambda_reg)
        
        grad_numerical[i] = (J_plus - J_minus) / (2 * epsilon)
    
    # 比较两个梯度
    diff = np.linalg.norm(grad_backprop - grad_numerical) / np.linalg.norm(grad_backprop + grad_numerical)
    
    print(f"梯度差异: {diff}")
    if diff < 1e-7:
        print("梯度检验通过！")
    else:
        print("梯度检验未通过，检查反向传播实现。")

重要：梯度检验很慢（要计算几千甚至几百万次代价函数），只在调试时使用。确认反向传播正确后，关闭梯度检验再进行正式训练。

随机初始化

在训练神经网络前，我们需要初始化权重。能不能像逻辑回归那样，把所有权重初始化为0？

答案是不能！如果所有权重都是0（或任何相同的值），那么同一层的所有神经元会计算相同的值，得到相同的梯度，进行相同的更新。即使经过多次迭代，同一层的所有神经元仍然会做同样的计算——这样多个神经元就没有意义了，相当于只有一个神经元。这个问题称为对称性问题（Symmetry Problem）。

解决方法是随机初始化（Random Initialization）：给每个权重赋一个随机的小值。

def randomInitialize(inputSize, outputSize, epsilon=0.12):
    """
    随机初始化权重矩阵
    权重在[-epsilon, epsilon]之间均匀分布
    """
    return np.random.rand(outputSize, inputSize + 1) * 2 * epsilon - epsilon
 
# 使用
Theta1 = randomInitialize(inputSize, hiddenSize)
Theta2 = randomInitialize(hiddenSize, outputSize)

为什么用小的随机值？

• 打破对称性：不同的初始值让不同神经元学习不同的特征
• 避免饱和：如果权重很大，$z = \Theta^T a$ 的绝对值会很大，sigmoid函数会饱和（接近0或1），梯度接近0，学习很慢

$\epsilon$ 的选择有一定的经验法则，比如 $\epsilon = \frac{\sqrt{6}}{\sqrt{L_{in} + L_{out}}}$，其中 $L_{in}$ 和 $L_{out}$ 是相邻两层的神经元数量。这称为Xavier初始化。

组合到一起：训练神经网络

现在我们有了所有的组件，可以把它们组合起来训练神经网络：

完整训练流程：

1. 选择网络架构：输入层大小（特征数）、输出层大小（类别数）、隐藏层数量和每层大小

2. 随机初始化权重：打破对称性

3. 实现前向传播：对于所有样本计算 $h_\Theta(x)$

4. 实现代价函数：计算 $J(\Theta)$

5. 实现反向传播：计算所有 $\frac{\partial J}{\partial \Theta_{ij}^{(l)}}$

6. 梯度检验：用数值方法验证反向传播的正确性，然后关闭它

7. 梯度下降（或其他优化算法）：重复迭代，不断更新权重

def trainNeuralNetwork(X, y, hiddenSize, numIter, alpha, lambda_reg):
    """
    训练神经网络
    """
    inputSize = X.shape[1] - 1  # 减去偏置
    outputSize = y.shape[1]
    
    # 1. 随机初始化
    Theta1 = randomInitialize(inputSize, hiddenSize)
    Theta2 = randomInitialize(hiddenSize, outputSize)
    
    # 2. 梯度下降
    J_history = []
    
    for i in range(numIter):
        # 前向传播
        a3 = forwardProp(X, Theta1, Theta2)
        
        # 计算代价
        J = computeCost(X, y, Theta1, Theta2, lambda_reg)
        J_history.append(J)
        
        # 反向传播
        Theta1_grad, Theta2_grad = backprop(X, y, Theta1, Theta2, lambda_reg)
        
        # 更新参数
        Theta1 -= alpha * Theta1_grad
        Theta2 -= alpha * Theta2_grad
        
        if (i+1) % 100 == 0:
            print(f"迭代 {i+1}: 代价 = {J:.4f}")
    
    return Theta1, Theta2, J_history

实际应用案例：手写数字识别

假设我们要识别28x28像素的手写数字（0-9）：

• 输入层：784个神经元（28 x 28像素）
• 隐藏层：25个神经元（可调）
• 输出层：10个神经元（10个数字类别）

# 加载数据
X_train, y_train = load_mnist_data()
 
# 预处理：归一化像素值到[0, 1]
X_train = X_train / 255.0
 
# One-hot编码标签
y_train_onehot = oneHotEncode(y_train, 10)
 
# 训练
Theta1, Theta2, J_history = trainNeuralNetwork(
    X_train, y_train_onehot,
    hiddenSize=25,
    numIter=1000,
    alpha=0.1,
    lambda_reg=1
)
 
# 评估
predictions = predict(X_test, Theta1, Theta2)
accuracy = np.mean(predictions == y_test)
print(f"测试准确率: {accuracy * 100:.2f}%")

通过调整网络架构、学习率、正则化参数，我们可以优化模型性能。

神经网络训练是一个迭代的过程。我们可能需要尝试不同的超参数，监控学习曲线，诊断问题（过拟合、欠拟合、梯度消失等）。别担心，我们马上就将学习如何系统地评估和改进机器学习系统，这些技术同样适用于神经网络。

反向传播算法虽然数学上有点复杂，但它让我们能够训练拥有数百万参数的深度网络，推动了深度学习革命。从图像识别到自然语言处理，从游戏AI到自动驾驶，反向传播都是背后的核心技术。

小练习

1. 计算反向传播的梯度：对于一个简单的神经网络，手动计算反向传播的梯度。

   网络：2个输入 → 2个隐藏神经元 → 1个输出

   给定：

   • 输入：$x = [1, 0.5]$（已加偏置）
   • 真实标签：$y = 1$
   • 隐藏层输出：$a^{(2)} = [1, 0.6, 0.7]$（已加偏置）
   • 最终输出：$a^{(3)} = 0.8$

   计算输出层的误差 $\delta^{(3)}$ 和隐藏层的误差 $\delta^{(2)}$。

import numpy as np
 
# 数据
x = np.array([[1], [0.5]])
y = 1
a2 = np.array([[1], [0.6], [0.7]])
a3 = 0.8
Theta2 = np.array([[0.5, 0.8, 0.9]])
 
# 输出层误差
delta3 = a3 - y
print(f"输出层误差 δ³: {delta3}")
 
# 隐藏层误差
sigmoid_gradient = a2[1:] * (1 - a2[1:])  # 去掉偏置
delta2 = (Theta2[:, 1:].T * delta3) * sigmoid_gradient
print(f"隐藏层误差 δ²: {delta2.flatten()}")

2. 梯度检验：实现数值梯度计算，验证反向传播的正确性。

   对于参数 $\theta_i$，数值梯度定义为： $\frac{\partial J}{\partial \theta_i} \approx \frac{J(\theta_i + \epsilon) - J(\theta_i - \epsilon)}{2\epsilon}$

   其中 $\epsilon = 10^{-4}$。编写Python代码实现梯度检验。

import numpy as np
 
def sigmoid(z):
    return 1 / (1 + np.exp(-z))
 
def compute_cost(X, y, theta1, theta2):
    """
    计算神经网络代价函数
    """
    m = X.shape[0]
    
    # 前向传播
    a1 = np.hstack([np.ones((m, 1)), X])
    z2 = a1 @ theta1.T
    a2 = sigmoid(z2)
    a2 = np.hstack([np.ones((m, 1)), a2])
    z3 = a2 @ theta2.T
    a3 = sigmoid(z3)
    
    # 代价函数（不含正则化）
    cost = -(1/m) * np.sum(y * np.log(a3) + (1-y) * np.log(1-a3))
    
    return cost
 
def numerical_gradient(X, y, theta1, theta2, epsilon=1e-4):
    """
    计算数值梯度
    """
    # 将参数展开成向量
    params = np.concatenate([theta1.ravel(), theta2.ravel()])
    numgrad = np.zeros_like(params)
    perturb = np.zeros_like(params)
    
    for i in range(len(params)):
        # 设置扰动
        perturb[i] = epsilon
        
        # 重构参数矩阵
        theta1_plus = (params + perturb)[:theta1.size].reshape(theta1.shape)
        theta2_plus = (params + perturb)[theta1.size:].reshape(theta2.shape)
        theta1_minus = (params - perturb)[:theta1.size].reshape(theta1.shape)
        theta2_minus = (params - perturb)[theta1.size:].reshape(theta2.shape)
        
        # 计算 J(theta + epsilon)
        loss_plus = compute_cost(X, y, theta1_plus, theta2_plus)
        
        # 计算 J(theta - epsilon)
        loss_minus = compute_cost(X, y, theta1_minus, theta2_minus)
        
        # 数值梯度
        numgrad[i] = (loss_plus - loss_minus) / (2 * epsilon)
        
        # 重置扰动
        perturb[i] = 0
    
    return numgrad
 
def backpropagation(X, y, theta1, theta2):
    """
    通过反向传播计算梯度
    """
    m = X.shape[0]
    
    # 前向传播
    a1 = np.hstack([np.ones((m, 1)), X])
    z2 = a1 @ theta1.T
    a2 = sigmoid(z2)
    a2 = np.hstack([np.ones((m, 1)), a2])
    z3 = a2 @ theta2.T
    a3 = sigmoid(z3)
    
    # 反向传播
    delta3 = a3 - y
    delta2 = (delta3 @ theta2[:, 1:]) * (a2[:, 1:] * (1 - a2[:, 1:]))
    
    # 梯度
    grad2 = (1/m) * (delta3.T @ a2)
    grad1 = (1/m) * (delta2.T @ a1)
    
    # 展开成向量
    grad = np.concatenate([grad1.ravel(), grad2.ravel()])
    
    return grad
 
# 测试
np.random.seed(42)
X = np.random.randn(5, 2)
y = np.random.randint(0, 2, (5, 1))
theta1 = np.random.randn(3, 3) * 0.1
theta2 = np.random.randn(1, 4) * 0.1
 
# 计算数值梯度
numgrad = numerical_gradient(X, y, theta1, theta2)
 
# 计算反向传播梯度
grad = backpropagation(X, y, theta1, theta2)
 
# 比较
difference = np.linalg.norm(numgrad - grad) / np.linalg.norm(numgrad + grad)
 
print(f"数值梯度前5个: {numgrad[:5]}")
print(f"反向传播梯度前5个: {grad[:5]}")
print(f"相对差异: {difference}")
 
if difference < 1e-7:
    print("✓ 梯度检验通过！反向传播实现正确。")
else:
    print("✗ 梯度检验失败！反向传播实现可能有误。")