支持向量机

在机器学习的算法家族中，支持向量机（Support Vector Machine, SVM）占据着特殊的地位。在深度学习兴起之前，SVM是最流行、最强大的监督学习算法之一。即使在今天，对于中小规模的数据集，SVM仍然是非常有竞争力的选择。

SVM的核心思想很简单：不仅要找到一个能正确分类的决策边界，还要找到“最好”的边界——离两类样本都尽可能远的边界。这种“最大间隔”的思想赋予了SVM良好的泛化能力。更进一步，通过核函数（Kernel），SVM能够高效地处理非线性问题，甚至可以在无限维空间中工作。

这一节课我们将学习SVM的基本原理、数学基础、核函数，以及如何在实践中使用SVM。我们会发现，SVM虽然数学上比较复杂，但核心思想其实很直观。

SVM的优化目标

让我们从逻辑回归开始，看看如何修改它得到SVM。回忆逻辑回归的代价函数。对于单个样本：

$-y \log(h_\theta(x)) - (1-y) \log(1-h_\theta(x))$

其中 $h_\theta(x) = \frac{1}{1 + e^{-\theta^T x}}$。

当 $y=1$ 时，我们希望 $h_\theta(x) \approx 1$，即 $\theta^T x \gg 0$（远大于0）。 当 时，我们希望 ，即 （远小于0）。

SVM做了一个简化：用两段线性函数代替逻辑回归的对数函数。这让优化变得更简单，同时保留了核心思想。

SVM的代价函数：

$\min_\theta C \sum_{i=1}^{m} [y^{(i)} \text{cost}_1(\theta^T x^{(i)}) + (1-y^{(i)}) \text{cost}_0(\theta^T x^{(i)})] + \frac{1}{2} \sum_{j=1}^{n} \theta_j^2$

这里：

• $\text{cost}_1(z)$ 是当 $y=1$ 时的代价，在 $z < 1$ 时线性增长，$z \geq 1$ 时为0

与逻辑回归相比，SVM的代价函数有两个不同：

1. 用分段线性函数代替对数函数
2. 把 $\frac{\lambda}{2}$ 正则化项移到前面，用 $C$ 控制权衡

SVM的决策函数：

$h_\theta(x) = \begin{cases} 1 & \text{if } \theta^T x \geq 0 \\ 0 & \text{otherwise} \end{cases}$

注意SVM直接输出0或1，不像逻辑回归输出概率。

大间隔分类器

SVM最显著的特点是它寻找“最大间隔”的决策边界。

想象在二维平面上有两类样本，用一条直线分隔它们。有无数条直线都能把两类正确分开。SVM不满足于“只是分开”，它要找到离两类样本都最远的那条线——这就是最大间隔。

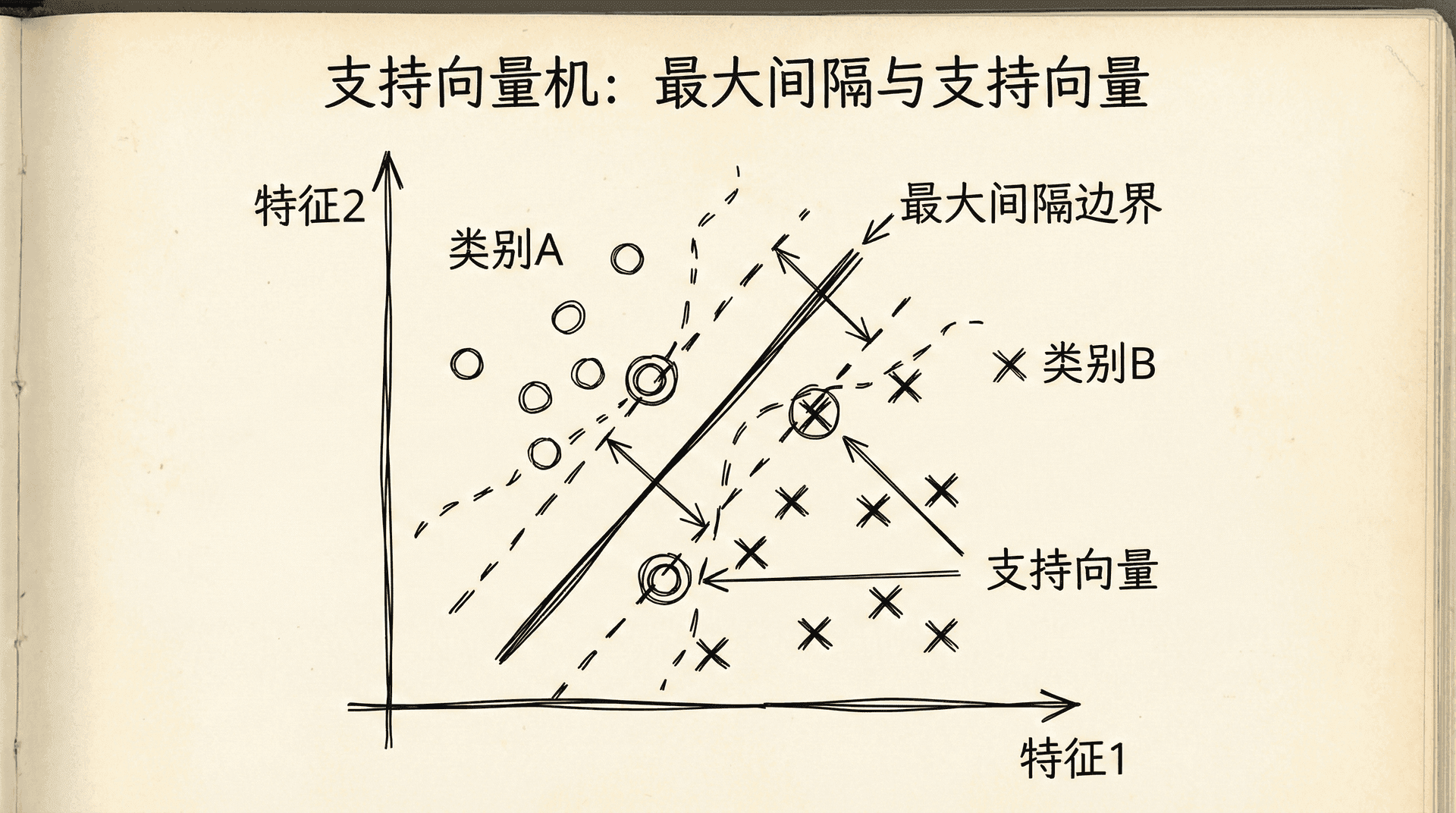
间隔（Margin） 是决策边界到最近样本的距离。SVM寻找能够最大化间隔的边界。

为什么最大间隔是好的？直觉上，如果决策边界离训练样本很远，那么：

• 模型对新数据更稳健——新样本有小的变化不会导致分类错误
• 模型具有更好的泛化能力
• 模型对噪声和异常值不那么敏感

从优化的角度看，当 $C$ 很大时（正则化很弱），SVM会尽力正确分类所有样本，同时最大化间隔。

数学表达：

SVM的优化目标可以等价地写成：

$\min_\theta \frac{1}{2} ||\theta||^2$

subject to: $\theta^T x^{(i)} \geq 1 \quad \text{if } y^{(i)} = 1$ ${\theta }^T{x}^{}$

这个形式清楚地表达了SVM的目标：在正确分类所有样本的约束下，最小化 $||\theta||^2$（即最大化间隔，因为间隔与 $||\theta||$ 成反比）。

支持向量就是那些刚好满足 $\theta^T x^{(i)} = 1$ 或 $\theta^T x^{(i)} = -1$ 的样本。它们定义了间隔的边界，也决定了决策边界的位置。

C参数的作用：

• $C$ 很大：SVM努力正确分类所有样本，间隔可能很小，可能过拟合
• $C$ 很小：SVM允许一些分类错误，换取更大的间隔，更稳健

在有噪声或不完全线性可分的数据中，适中的 $C$ 能在拟合数据和泛化能力之间取得平衡。

核函数：处理非线性

到目前为止，我们讨论的都是线性分类器。但很多实际问题是非线性的——无法用一条直线（或超平面）完美分开。

对于逻辑回归，我们通过添加多项式特征来处理非线性。但对于高维数据，多项式特征的数量会爆炸式增长。

SVM提供了一个更优雅的解决方案：核函数（Kernel）。核函数让我们能够在高维甚至无限维空间中工作，而不需要显式地计算那些高维特征。

基本思想：

与其添加多项式特征 $x_1^2, x_1 x_2, x_2^2, ...$，我们定义新的特征基于与某些"地标"（landmarks）的相似度。

选择一些点 $l^{(1)}, l^{(2)}, ..., l^{(m)}$ 作为地标（通常选训练样本本身）。对于样本 $x$，新特征是：

$f_i = \text{similarity}(x, l^{(i)}) = \exp\left(-\frac{||x - l^{(i)}||^2}{2\sigma^2}\right)$

这个相似度函数称为高斯核（Gaussian Kernel）或径向基函数（RBF Kernel）。

高斯核的性质：

• 当 $x \approx l^{(i)}$ 时，$f_i \approx 1$（很相似）
• 当 $x$ 远离 ${}^{}$ 时，（不相似）

用这些新特征替代原始特征，SVM的决策函数变成：

$h_\theta(x) = \theta_0 + \theta_1 f_1 + \theta_2 f_2 + ... + \theta_m f_m$

如果 $x$ 接近某些正类样本，对应的 $f_i$ 就大，$h_\theta(x)$ 就可能大于0，预测为正类。

核函数的魔力在于：我们不需要显式计算所有 $f_i$。在SVM的优化中，只需要计算核函数 $k(x^{(i)}, x^{(j)})$ 在样本对之间的值。这使得计算非常高效。

常用的核函数：

1. 线性核（Linear Kernel）：

$k(x, x') = x^T x'$

就是普通的内积，等价于不用核函数。

2. 多项式核（Polynomial Kernel）：

$k(x, x') = (x^T x' + c)^d$

其中 $d$ 是多项式的次数。

3. 高斯核（RBF Kernel）：

$k(x, x') = \exp\left(-\frac{||x - x'||^2}{2\sigma^2}\right)$

也可以写成 $k(x, x') = \exp(-\gamma ||x - x'||^2)$，其中 。

4. Sigmoid核：

$k(x, x') = \tanh(\alpha x^T x' + c)$

类似神经网络的激活函数。

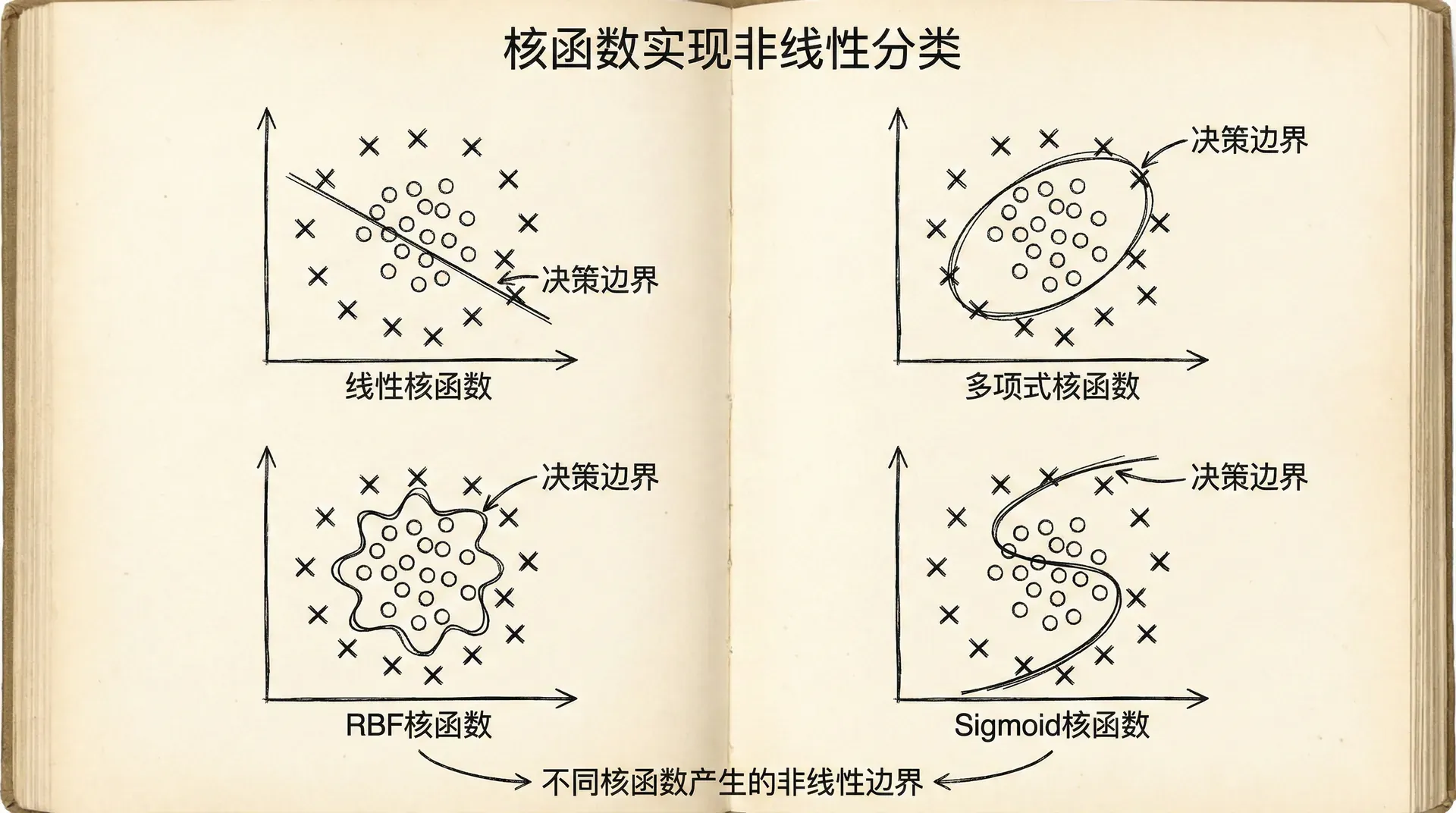
核函数的选择：

• 线性核：特征数量远大于样本数量时（如文本分类），或数据本身线性可分
• RBF核：通用选择，适合大多数情况，特别是特征数量较少、样本数量适中时
• 多项式核：适合特定的非线性关系，但需要调整次数 $d$

实践中，RBF核是最常用的。

使用SVM

在实践中，我们通常使用成熟的SVM库（如scikit-learn的SVC），而不是自己实现优化算法。使用SVM时需要做的主要决策是：

1. 选择核函数

根据问题特点和数据规模选择。

2. 选择参数

对于RBF核：

• $C$：正则化参数。$C$ 大：低偏差，高方差（可能过拟合）；$C$ 小：高偏差，低方差
• $\gamma$ (或 $\sigma^2$)：核函数的宽度。$\gamma$ 大：影响范围小，可能过拟合；$$ 小：影响范围大，可能欠拟合

这些参数通常通过网格搜索和交叉验证来选择。

|
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
from sklearn.preprocessing import StandardScaler
 
# 特征缩放（重要！）
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
 
# 定义参数网格
param_grid = {
    'C': [0.1, 1, 10, 100],
    'gamma'

3. 特征缩放

SVM对特征的尺度敏感。使用RBF核时，必须进行特征缩放（标准化或归一化）。

4. 多分类

SVM本身是二分类器。对于多分类问题，库通常使用一对多（One-vs-Rest）或一对一（One-vs-One）策略。

SVM vs 逻辑回归 vs 神经网络：

何时使用SVM？

• $n$ 大（特征多），$m$ 小（样本少）：使用线性核的SVM或逻辑回归
• $n$ 小，$m$ 适中：使用RBF核的SVM
• $n$ 小，$m$ 大：增加更多特征，然后使用逻辑回归或线性核SVM

何时使用神经网络？

• 数据量很大时，神经网络通常表现更好
• 需要端到端学习（如图像、语音）时

何时使用逻辑回归？

• 需要概率输出时
• 模型需要易于解释时
• 特征数量很大时

SVM的优点：

• 在中小规模数据上通常表现很好
• 核技巧使它能有效处理高维数据
• 有理论保证（统计学习理论）
• 不需要大量调参就能获得不错的性能

SVM的缺点：

• 对大规模数据（百万级样本）较慢
• 核函数和参数的选择不总是直观
• 不直接输出概率（虽然可以通过额外计算得到）
• 对噪声和异常值敏感（可以用软间隔SVM缓解）

SVM的数学直觉

虽然SVM的完整数学推导涉及优化理论和对偶问题，但核心思想可以直观理解。

最大间隔的几何意义：

决策边界是 $\theta^T x = 0$。点 $x$ 到这个超平面的距离是 $\frac{|\theta^T x|}{||\theta||}$。

间隔就是最近点到超平面的距离。最大化间隔等价于：

1. 确保所有点到决策边界的距离至少为某个值（比如 $\frac{1}{||\theta||}$）
2. 最大化这个最小距离，即最小化 $||\theta||$

这就是为什么SVM的目标是最小化 $\frac{1}{2}||\theta||^2$（平方是为了数学方便）。

支持向量的作用：

在最优解中，只有支持向量对决策边界有影响。其他样本（离边界远的）的位置改变不会影响决策边界。这使得SVM对异常值相对稳健——只要异常值不是支持向量，它们就不会影响模型。

核技巧的数学：

SVM的优化实际上只依赖于样本之间的内积 $x^{(i)} \cdot x^{(j)}$。核函数 $k(x^{(i)}, x^{(j)})$ 计算的是特征映射后的内积，但不需要显式计算映射后的特征向量。

实践案例

让我们看一个完整的例子：使用SVM进行手写数字识别。

|
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import classification_report, confusion_matrix
import numpy as np
 
# 加载数据
digits = load_digits()
X, y = digits.data, digits.target
 
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, 

支持向量机是机器学习中的经典算法，它体现了简单的数学思想和强大的实践性能。虽然在深度学习时代，SVM不再是最热门的算法，但它在很多场景下仍然是非常有价值的工具。重要的是，学习SVM能让我们理解很多重要的机器学习概念——间隔、核函数、对偶问题——这些概念在其他算法和理论中也经常出现。

在下一节课中，我们将转向无监督学习，学习K-Means聚类算法。与监督学习不同，无监督学习处理的是没有标签的数据，目标是发现数据中的内在结构和模式。

小练习

1. 问题诊断和解决方案：根据以下情况，诊断问题并提出解决方案。

   你训练了一个模型，得到：

   • 训练误差：5%
   • 验证误差：25%

   这是什么问题？应该如何解决？

|
def diagnose_model(train_error, val_error):
    gap = val_error - train_error
    
    if train_error > 0.15:  # 高偏差
        if gap < 0.05:
            return "欠拟合（高偏差）"
        else:

2. 学习曲线分析：分析以下学习曲线，判断问题类型。

   随着训练样本数量增加：

   • 训练误差：从10%缓慢上升到18%
   • 验证误差：从60%缓慢下降到20%
   • 两条曲线在20%附近趋于平缓，但仍有差距

   这是什么问题？解决方案是什么？

|
高方差（过拟合）：
  训练误差：很低且平
  验证误差：高且有大gap
  解决：更多数据有帮助
  
高偏差（欠拟合）：
  训练误差：高且平
  验证误差：高且gap小
  解决：更多数据帮助不大，需要更复杂模型
  
理想状态：
  两条曲线都低且接近
  差距很小