词向量进阶 - 负采样与GloVe | 自在学词向量进阶
在上一部分中,我们学习了Word2Vec的基本框架,特别是Skip-gram模型。该模型通过最大化对数似然来学习词向量:
J(θ)=T1t=1∑T−m≤j≤mj=0∑logP(wt+j∣wt)
其中条件概率使用Softmax函数定义:
P(o∣c)=∑w∈Vexp(
然而,这个公式存在一个严重的计算瓶颈:分母需要对整个词汇表求和。对于包含10万词的词汇表,每次更新参数都需要计算10万次指数和点积,这在大规模语料训练中是不可接受的。
面对朴素Softmax的计算困境,研究者们开发了多种巧妙的优化策略。负采样(Negative Sampling)将多分类问题转化为多个二分类,每次只需要计算少量词的概率,而非整个词汇表——这使得Word2Vec能在数十亿词的语料上高效训练。
**分层Softmax(Hierarchical Softmax)**则利用树结构,将计算复杂度从O(∣V∣)降至O(log∣V∣),就像用二叉搜索代替线性搜索一样高效。
而GloVe算法提供了一个全新的视角——与其用神经网络在局部窗口上学习,为什么不先统计全局的词共现信息,然后直接对共现矩阵进行因式分解?这种“全局统计+局部上下文”的思想让GloVe在许多任务上与Word2Vec效果相当甚至更好。
这部分我们将深入探讨词向量的评估方法——如何量化测量词向量的质量?词类比任务(“国王-男人+女人=女王”)能否真正反映语义理解?词向量空间有什么几何性质?这些问题的答案将帮助我们更深入地理解词嵌入的本质。
负采样
在原始的Skip-gram模型中,对于每个训练样本(中心词 c,上下文词 o),损失函数为:
L=−logP(o∣c)=−log∑
让我们分析这个公式的计算代价。在前向传播中,分母需要对整个词汇表的∣V∣个词计算点积和指数运算。在反向传播中,梯度会流向所有∣V∣个上下文词向量,每个都需要更新。因此,每个训练样本的总复杂度是O(∣V∣)——对于一个包含10万词的词汇表,每次参数更新都要计算10万次!
当我们在包含数十亿词的大规模语料上训练时,这种复杂度完全不可接受。假设语料有10亿词,窗口大小为10,那么训练样本数量约为100亿(10亿词×10个上下文位置)。如果每个样本需要O(105)次运算,总计算量达到1015次运算——即使在现代GPU上也需要数月时间。这就是Word2Vec面临的计算瓶颈。
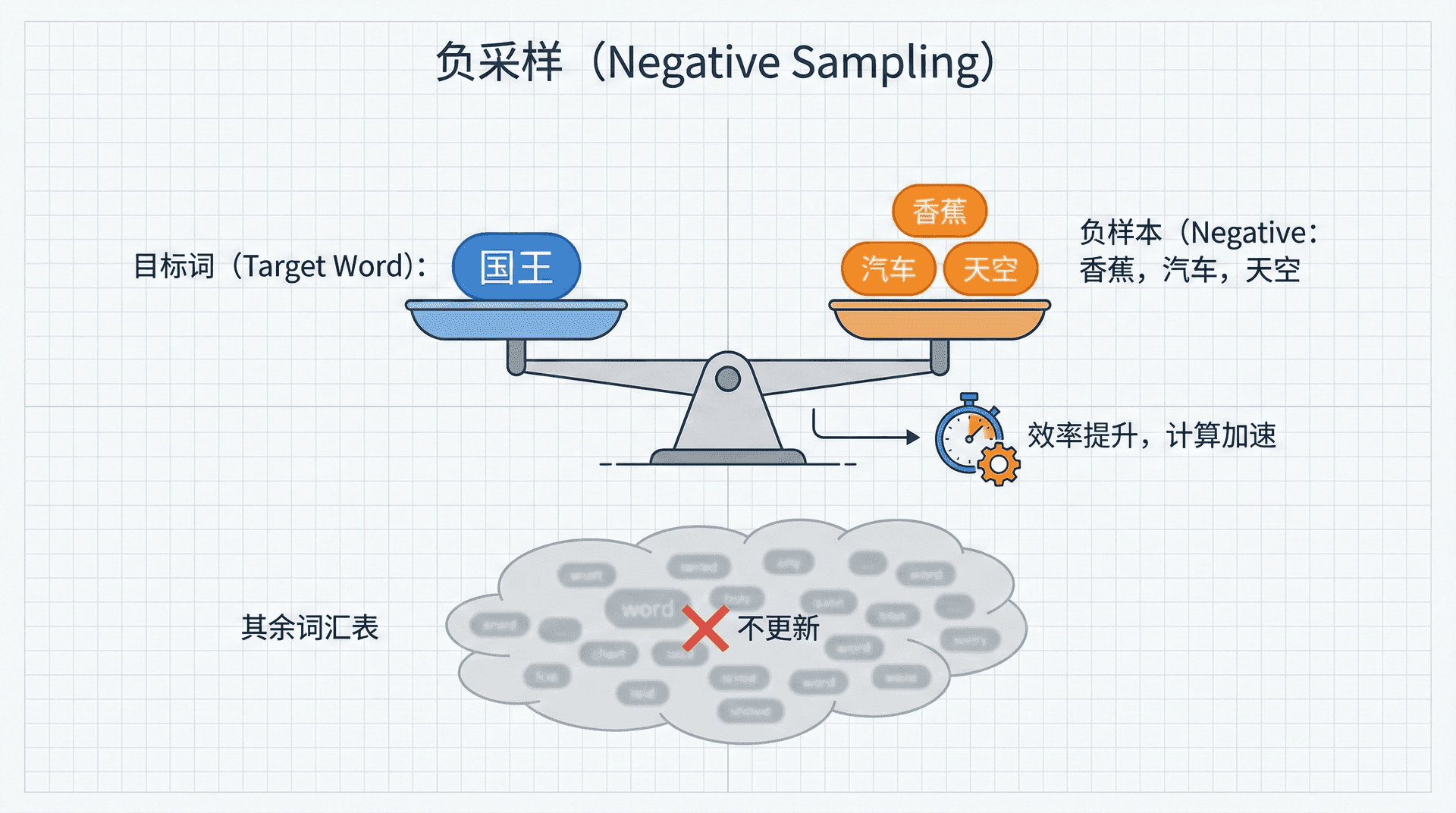
负采样(Negative Sampling)由Mikolov等人在2013年提出,核心思想是将多分类问题转化为二分类问题。
原问题是一个多分类任务:在∣V∣个候选词中找出正确的上下文词。负采样将其转化为更简单的二分类任务:判断给定的词对(c,w)是否真正来自语料中的上下文窗口。
具体来说,对于每个真实的词对——中心词c和其上下文词o——我们标记为正样本(标签为1)。然后随机采样k个词(通常k=5到k=20),这些词不是c的真实上下文,标记为负样本(标签为0)。现在任务变成了训练一个二分类模型,学习区分真实共现和随机组合。
这个转化的妙处在于:我们不再需要归一化整个词汇表,只需要对k+1个词(1个正样本+k个负样本)计算概率。计算复杂度从O(∣V∣)降到O(k),而k通常远小于——这带来了数千倍的加速!
数学推导
目标函数
对于中心词 c 和词 w,定义它们共现的概率为:
P(D=1∣c,w)=σ(u
其中 σ 是sigmoid函数,D=1 表示 (c,w) 是真实共现对。
相应地,不共现的概率为:
P(D=0∣c,w)=1−σ(u
负采样目标函数
对于中心词c和上下文词o,我们希望达到两个目标:让模型认为真实的词对(c,o)确实共现(最大化其概率),同时让模型认为随机采样的k个负样本(c,wi不太可能共现(最小化其概率)。这两个目标可以用一个统一的目标函数表达:
JNEG(c,o)=−log
其中:
- Pn(w) 是负采样分布
- k 是负样本数量,通常取5-20
直观地理解这个目标函数:第一项−logσ(uoTv鼓励真实上下文词的sigmoid输出接近1,即应该是一个大的正数。第二项鼓励负样本词的sigmoid输出接近0,即应该是负数或接近0。通过最小化这个目标,模型学会让语义相关的词向量相近(点积大),不相关的词向量疏远(点积小)。
梯度计算
对中心词向量 vc 求偏导:
∂v
利用sigmoid函数的导数性质 dxdlogσ(x)=1−σ(x):
∂v
=(σ(u
从计算复杂度看,这是一个巨大的胜利。原始Softmax每次更新需要O(∣V∣)次运算——对10万词的词汇表就是10万次。负采样只需要O(k)次运算,而k通常取5到20,比∣V∣小几千倍甚至上万倍。这不仅加速了训练,也使得在普通硬件上训练大规模词向量成为可能——Mikolov等人在一台机器上用一天时间训练了包含数十亿词的语料,这在Softmax时代是不可想象的。
负采样分布的选择
如何选择负样本至关重要。Mikolov等人提出使用单词频率的43次方:
Pn(w)=∑w
其中 f(w) 是词 w 在语料中的频率。
为什么使用43次方?
-
均匀分布 (Pn(w)=∣V∣1):所有词被采样的概率相同,但这会导致高频词(如"的"、"了")被过度采样
-
原始频率 ():按词频采样,但高频词占主导,低频词几乎不被采样
数值示例:
假设三个词的频率分布为:
- f(的)=0.1
- f(学习)=0.001
- f(量子)=0.0001
不同采样策略下的概率:
可见,43次方显著提升了低频词的采样概率。
分层Softmax
分层Softmax(Hierarchical Softmax)是另一种加速训练的方法,通过将词汇表组织成二叉树结构,将 O(∣V∣) 的复杂度降至 O(log∣V∣)。
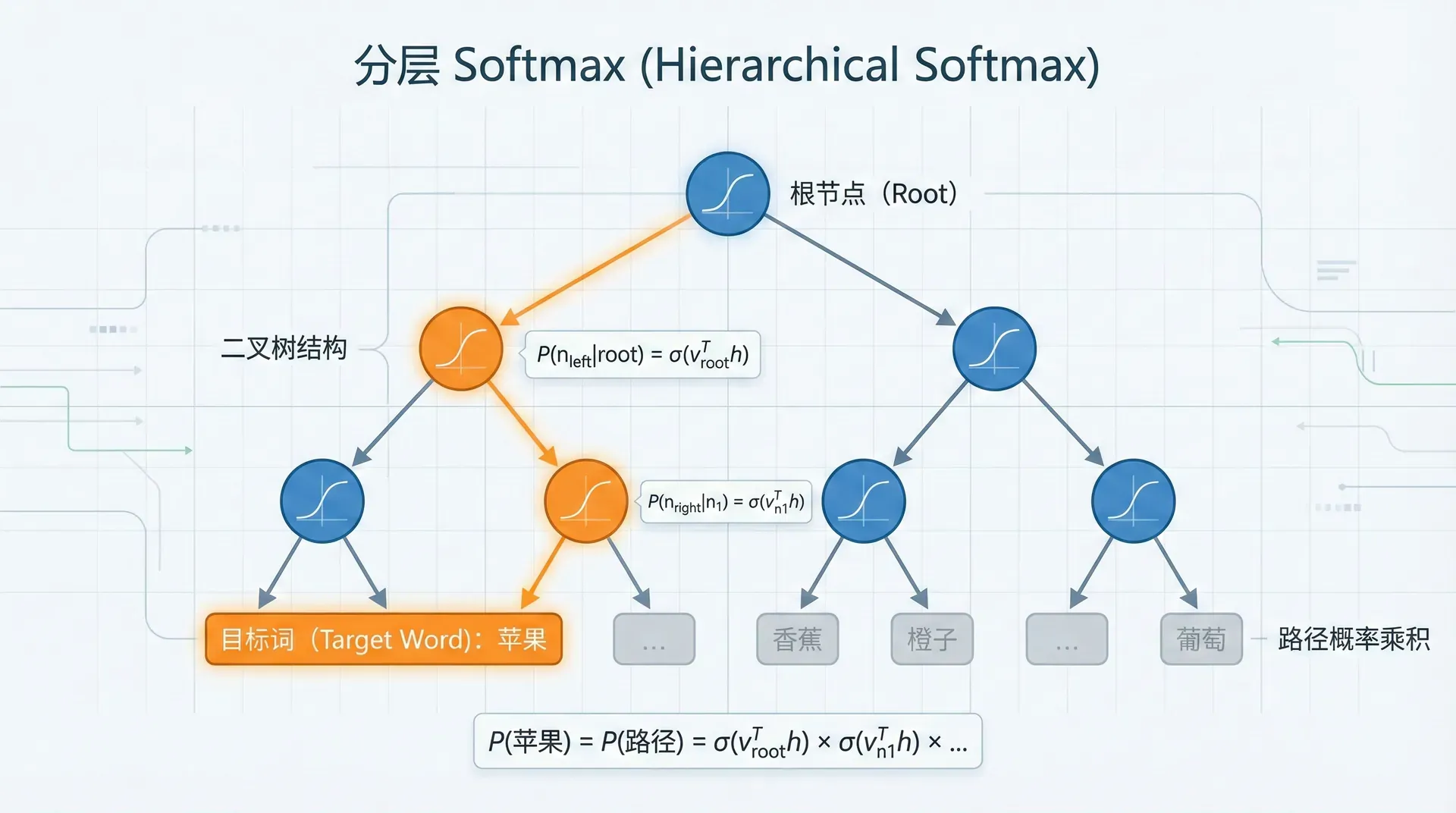
树结构设计
哈夫曼树:根据词频构建哈夫曼树,高频词距离根节点更近。
- 每个词是叶子节点
- 每个内部节点对应一个向量(称为路径向量)
- 从根到叶子的路径唯一确定一个词
示例树结构:
根(θ₁)
/ \
(θ₂) (θ₃)
/ \ / \
w₁ w₂ w₃ w₄
概率计算
对于词 w,定义从根到 w 的路径为 path(w)=(n1,n2,其中 是根, 是 的父节点。
在每个内部节点 n,做一个二分类决策:
- 向左走:概率 σ(θnTv
词 w 的概率是路径上所有决策概率的乘积:
P(w∣c)=i=1∏L−1σ
其中 [[条件]] 是指示函数,条件为真时为1,否则为-1。
优缺点分析
优势:
- 计算复杂度显著降低:O(log∣V∣)
- 不需要负采样
- 理论上严格的概率模型
劣势:
- 需要预先构建树结构
- 更新路径向量的梯度计算较复杂
- 实践中负采样通常更受欢迎(更简单、效果相当)
GloVe算法
动机与核心思想
GloVe(Global Vectors for Word Representation)由斯坦福团队(Pennington, Socher, Manning, 2014)提出,旨在结合两类方法的优势:
计数方法(如LSA):
- 利用全局共现统计信息
- 训练速度快
- 但在词类比任务上表现较差
预测方法(如Word2Vec):
- 利用局部窗口信息
- 词类比任务表现好
- 但未充分利用全局统计
GloVe模型推导
共现矩阵
首先构建词-词共现矩阵 X:
- Xij:词 i 和词 j 在窗口内共现的次数
- Xi=:词 的总共现次数
目标函数设计
我们希望学习词向量,使得它们的点积与共现概率的比值相关。设计函数 F:
F(wi,w
为了使向量空间具有线性结构,要求 F 满足:
F(wi−
进一步,假设 F 只依赖于向量点积:
F((w
解这个函数方程,得到 F=exp,因此:
wiT
最终目标函数
引入偏置项 bi 和 b~k 来吸收 logX:
wiT
加入权重函数 f(Xij) 来处理不同频率的共现对,最终目标函数为:
J=i,j=1∑∣V∣f(
权重函数 f(Xij):
f(x)={(x/xmax)
通常取 xmax=100,α=0.75。
权重函数的作用:
- 稀有共现(Xij 很小):权重较小,避免噪声影响
- 极高频共现(如停用词):权重被截断,避免主导训练
- 中等频率共现:权重较大,是学习的主要信号
GloVe训练算法
算法:GloVe训练
输入:共现矩阵 X, 向量维度 d, 迭代次数 epochs
输出:词向量 W, W̃
1. 初始化 W, W̃, b, b̃ 为小随机值
2. for epoch = 1 to epochs:
3. for (i, j) where X_ij > 0:
4. 计算权重 w_ij = f(X_ij)
5. 计算梯度:
GloVe vs. Word2Vec
代码实现
带负采样的Skip-gram实现
import torch
import torch.nn as nn
import numpy as np
from collections import Counter
class SkipGramNegSampling(nn.Module):
"""带负采样的Skip-gram模型"""
def __init__(self, vocab_size, embedding_dim):
super(SkipGramNegSampling, self).__init__()
self.vocab_size = vocab_size
简单的GloVe实现
import torch
import torch.nn as nn
import numpy as np
from scipy import sparse
class GloVeModel(nn.Module):
"""GloVe模型实现"""
def __init__(self, vocab_size, embedding_dim):
super(GloVeModel, self).__init__()
self.vocab_size = vocab_size
self
词向量评估
内在评估方法
词类比任务
任务定义:给定词对 (a,b) 和词 c,找出词 d 使得“a 之于 b 正如 c 之于 d”。
示例:
- 语义类比:“国王” - “男人” + “女人” ≈ “女王”
- 句法类比:“慢” - “慢慢” + “快” ≈ “快快”
评估方法:
d∗=argd∈V
排除 a,b,c 本身,计算余弦相似度最高的词。
标准数据集:
- Google Analogy Dataset:19,544个语义和句法类比
- BATS(Bigger Analogy Test Set)
词相似度任务
任务定义:计算词对之间的相似度,与人类标注相似度比较。
评估指标:Spearman相关系数
标准数据集:
- WordSim-353
- SimLex-999
- 中文:WordSim-296 (Chinese)
计算方法:
similarity(w1,w2)=
外在评估方法
将词向量作为特征用于下游任务,评估任务性能:
- 命名实体识别(NER):识别人名、地名、组织名等
- 词性标注(POS Tagging):标注词的语法类别
- 情感分析:判断文本的情感倾向
- 文本分类:将文本分配到预定义类别
评估指标:准确率、F1分数等
评估代码示例
import numpy as np
from scipy.stats import spearmanr
def evaluate_analogy(word_vectors, vocab, test_cases):
"""
评估词类比任务
Args:
word_vectors: 词向量矩阵 (vocab_size, embedding_dim)
vocab: 词到索引的字典
test_cases: [(a, b, c, d)] 类比测试用例
Returns:
准确率
"""
correct = 0
total = 0
for a, b, c, d in test_cases:
练习与思考
-
解释为什么负采样能够大幅降低计算复杂度。从目标函数的角度分析原始Softmax和负采样的区别。
-
在负采样中,为什么使用 f(w)0.75 而不是原始词频 f(w) 作为采样分布?这对高频词和低频词的训练有什么影响?
-
GloVe的权重函数 f(Xij 在 时递增,在 时截断为1。解释这种设计的合理性。
dxdlogσ(x)=1−σ(x)
- 实现一个高效的负采样器,使用别名采样(Alias Sampling)方法,将采样复杂度从 O(∣V∣) 降至 O(1)。
class AliasNegativeSampler:
"""使用别名采样的高效负采样器"""
def __init__(self, word_counts, power=0.75):
# 你的实现
pass
def sample(self, k):
"""O(1)复杂度采样k个负样本"""
pass
- 在实际数据集上训练并比较Word2Vec和GloVe:
- 使用中文维基百科语料
- 在词类比和词相似度任务上评估
- 分析两种方法的性能差异
- 实现一个词向量可视化工具,使用t-SNE将高维词向量投影到2D平面,观察词聚类现象。
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
def visualize_embeddings(word_vectors, words, output_file='embeddings.png'):
"""
可视化词向量
Args:
word_vectors: 词向量数组 (n, dim)
words: 词列表
output_file: 输出图片路径
"""
# 你的实现
pass
接下来
这节课我们总结了词向量学习的核心优化方法,包括负采样、分层Softmax和GloVe等技术,它们大幅降低了模型计算复杂度并提升了训练效率。
这些方法实际上都在利用词语的共现统计信息,通过合适的采样分布设计、合理的模型结构或全局统计,优化词向量的表达能力,并通过词类比、词相似度等任务进行评估。
然而,传统静态词向量存在一些局限,如无法区分一词多义、难以处理未登录词(OOV)及缺乏对句子和文档级别语义的建模。因此,子词模型和上下文动态建模成为后续研究方向。下一节我们将回顾一些神经网络的基础知识,为深入学习RNN、LSTM等更强大的序列建模方法奠定基础。
u
wT
)
w∈V
exp
(
)
∣V∣
wT
)
=
wT
)
=
)
σ
(
)
−
i=1∑kEwi∼Pn(w)[logσ(−uwiTvc)] c
)
uoTvc −∑ilogσ(−uwiTvc) uwiTvc c
∂JNEG
=
i=1∑k∂vc∂logσ(−uwiTvc) c
∂JNEG
=
−(1−
i=1∑k(1−
o
T
)
−
′
∈
V
f
(
w′
)3/4
f(w)3/4
Pn(w)=f(w)
43次方 (Pn(w)∝f(w)3/4):折中方案,既考虑频率,又给低频词更多机会
,
…
,
nL
)
c
)
向右走:概率 1−σ(θnTvc)
([[ni+1=left(ni)]]⋅θniTvc)
∑kXik
Pij=P(j∣i)=Xij/Xi:条件概率 j
,
)
=
PjkPik
w
j
,
)
=
PjkPik
i
−
~
k
=
logPik=
logXik−
logXi
i
w
~
k
+
bi+
b~k=
logXik
X
ij
)
(wiTw~j+bi+b~j−logXij)2 α
1
if x<xmaxotherwise
6. diff = w_i^T w̃_j + b_i + b̃_j - log(X_ij)
7. ∇J_w_i = w_ij * diff * w̃_j
8. ∇J_w̃_j = w_ij * diff * w_i
9. ∇J_b_i = w_ij * diff
10. ∇J_b̃_j = w_ij * diff
11. 更新参数(使用AdaGrad等优化器)
12. 返回 W 和 W̃ 的平均作为最终词向量
self.embedding_dim = embedding_dim
# 中心词嵌入
self.center_embeddings = nn.Embedding(vocab_size, embedding_dim)
# 上下文词嵌入
self.context_embeddings = nn.Embedding(vocab_size, embedding_dim)
# 初始化
self._init_weights()
def _init_weights(self):
"""初始化权重"""
init_range = 0.5 / self.embedding_dim
self.center_embeddings.weight.data.uniform_(-init_range, init_range)
self.context_embeddings.weight.data.uniform_(-init_range, init_range)
def forward(self, center_words, pos_contexts, neg_contexts):
"""
Args:
center_words: (batch_size,) 中心词索引
pos_contexts: (batch_size,) 正样本上下文词索引
neg_contexts: (batch_size, k) k个负样本索引
Returns:
loss: 负采样损失
"""
batch_size, k = neg_contexts.shape
# 获取词向量
# (batch_size, embedding_dim)
center_embeds = self.center_embeddings(center_words)
# (batch_size, embedding_dim)
pos_embeds = self.context_embeddings(pos_contexts)
# (batch_size, k, embedding_dim)
neg_embeds = self.context_embeddings(neg_contexts)
# 计算正样本得分
# (batch_size,)
pos_score = torch.sum(center_embeds * pos_embeds, dim=1)
pos_loss = -torch.log(torch.sigmoid(pos_score))
# 计算负样本得分
# (batch_size, k)
neg_score = torch.bmm(neg_embeds, center_embeds.unsqueeze(2)).squeeze(2)
neg_loss = -torch.sum(torch.log(torch.sigmoid(-neg_score)), dim=1)
# 总损失
loss = torch.mean(pos_loss + neg_loss)
return loss
def get_embedding(self, word_idx):
"""获取词向量(中心词+上下文词的平均)"""
center_vec = self.center_embeddings.weight[word_idx].detach().cpu().numpy()
context_vec = self.context_embeddings.weight[word_idx].detach().cpu().numpy()
return (center_vec + context_vec) / 2
class NegativeSampler:
"""负采样器"""
def __init__(self, word_counts, power=0.75):
"""
Args:
word_counts: 词频字典 {word_idx: count}
power: 词频的幂次,默认0.75
"""
# 计算采样概率
vocab_size = len(word_counts)
self.vocab_size = vocab_size
# 构建概率分布
word_freqs = np.array([word_counts.get(i, 0) for i in range(vocab_size)])
word_freqs = np.power(word_freqs, power)
self.probs = word_freqs / np.sum(word_freqs)
def sample(self, batch_size, k):
"""
采样负样本
Args:
batch_size: 批次大小
k: 每个样本的负样本数量
Returns:
(batch_size, k) 负样本索引
"""
neg_samples = np.random.choice(
self.vocab_size,
size=(batch_size, k),
p=self.probs,
replace=True
)
return torch.LongTensor(neg_samples)
# 训练示例
def train_skipgram_neg_sampling(model, data_loader, neg_sampler, epochs=10, lr=0.01, k=5):
"""
训练带负采样的Skip-gram
Args:
model: SkipGramNegSampling模型
data_loader: 数据加载器,返回(center_words, context_words)
neg_sampler: 负采样器
epochs: 训练轮数
lr: 学习率
k: 负样本数量
"""
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
for epoch in range(epochs):
total_loss = 0
num_batches = 0
for center_words, pos_contexts in data_loader:
batch_size = center_words.size(0)
# 采样负样本
neg_contexts = neg_sampler.sample(batch_size, k)
# 前向传播
optimizer.zero_grad()
loss = model(center_words, pos_contexts, neg_contexts)
# 反向传播
loss.backward()
optimizer.step()
total_loss += loss.item()
num_batches += 1
avg_loss = total_loss / num_batches
print(f"Epoch {epoch + 1}/{epochs}, Loss: {avg_loss:.4f}")
# 使用示例
if __name__ == "__main__":
# 假设已经预处理好数据
vocab_size = 10000
embedding_dim = 100
k_negative = 5
# 创建模型
model = SkipGramNegSampling(vocab_size, embedding_dim)
# 假设word_counts是词频统计
word_counts = {i: np.random.randint(1, 1000) for i in range(vocab_size)}
neg_sampler = NegativeSampler(word_counts, power=0.75)
print("模型创建成功!")
print(f"中心词嵌入维度: {model.center_embeddings.weight.shape}")
print(f"上下文词嵌入维度: {model.context_embeddings.weight.shape}")
.embedding_dim
=
embedding_dim
# 主词向量
self.w_embeddings = nn.Embedding(vocab_size, embedding_dim)
# 上下文词向量
self.w_tilde_embeddings = nn.Embedding(vocab_size, embedding_dim)
# 偏置项
self.w_biases = nn.Embedding(vocab_size, 1)
self.w_tilde_biases = nn.Embedding(vocab_size, 1)
# 初始化
self._init_weights()
def _init_weights(self):
"""随机初始化参数"""
init_range = 0.5 / self.embedding_dim
self.w_embeddings.weight.data.uniform_(-init_range, init_range)
self.w_tilde_embeddings.weight.data.uniform_(-init_range, init_range)
self.w_biases.weight.data.zero_()
self.w_tilde_biases.weight.data.zero_()
def forward(self, i_indices, j_indices, co_occurrences, weights):
"""
Args:
i_indices: (batch_size,) 词i的索引
j_indices: (batch_size,) 词j的索引
co_occurrences: (batch_size,) log(X_ij)
weights: (batch_size,) f(X_ij)权重
Returns:
loss: 加权平方损失
"""
# 获取词向量和偏置
w_i = self.w_embeddings(i_indices)
w_tilde_j = self.w_tilde_embeddings(j_indices)
b_i = self.w_biases(i_indices).squeeze()
b_tilde_j = self.w_tilde_biases(j_indices).squeeze()
# 计算内积
inner_product = torch.sum(w_i * w_tilde_j, dim=1)
# 计算差异
diff = inner_product + b_i + b_tilde_j - co_occurrences
# 加权平方损失
loss = weights * (diff ** 2)
return torch.mean(loss)
def get_embedding(self, word_idx):
"""获取最终词向量(W和W̃的平均)"""
w = self.w_embeddings.weight[word_idx].detach().cpu().numpy()
w_tilde = self.w_tilde_embeddings.weight[word_idx].detach().cpu().numpy()
return (w + w_tilde) / 2
def compute_weight(x, x_max=100, alpha=0.75):
"""
计算GloVe权重函数
Args:
x: 共现次数
x_max: 最大共现次数阈值
alpha: 幂次参数
Returns:
权重值
"""
return np.where(x < x_max, (x / x_max) ** alpha, 1.0)
def build_cooccurrence_matrix(corpus, vocab, window_size=5):
"""
构建共现矩阵
Args:
corpus: 词索引序列列表
vocab: 词汇表字典
window_size: 窗口大小
Returns:
稀疏共现矩阵
"""
vocab_size = len(vocab)
cooccur_matrix = sparse.lil_matrix((vocab_size, vocab_size), dtype=np.float32)
for sentence in corpus:
for i, center_word in enumerate(sentence):
# 左侧上下文
start = max(0, i - window_size)
for j in range(start, i):
context_word = sentence[j]
distance = i - j
cooccur_matrix[center_word, context_word] += 1.0 / distance
# 右侧上下文
end = min(len(sentence), i + window_size + 1)
for j in range(i + 1, end):
context_word = sentence[j]
distance = j - i
cooccur_matrix[center_word, context_word] += 1.0 / distance
# 转换为COO格式用于训练
return cooccur_matrix.tocoo()
# 训练函数
def train_glove(model, cooccur_matrix, epochs=50, lr=0.05, x_max=100, alpha=0.75):
"""
训练GloVe模型
Args:
model: GloVe模型
cooccur_matrix: 共现矩阵(scipy.sparse格式)
epochs: 训练轮数
lr: 学习率
x_max: 权重函数参数
alpha: 权重函数参数
"""
optimizer = torch.optim.Adagrad(model.parameters(), lr=lr)
# 提取非零元素
i_indices = torch.LongTensor(cooccur_matrix.row)
j_indices = torch.LongTensor(cooccur_matrix.col)
co_occur_values = torch.FloatTensor(cooccur_matrix.data)
log_co_occur = torch.log(co_occur_values)
# 计算权重
weights = compute_weight(co_occur_values.numpy(), x_max, alpha)
weights = torch.FloatTensor(weights)
num_samples = len(i_indices)
print("开始训练GloVe...")
for epoch in range(epochs):
# 打乱数据
perm = torch.randperm(num_samples)
i_shuffled = i_indices[perm]
j_shuffled = j_indices[perm]
log_co_shuffled = log_co_occur[perm]
weights_shuffled = weights[perm]
total_loss = 0
batch_size = 4096
num_batches = (num_samples + batch_size - 1) // batch_size
for batch_idx in range(num_batches):
start = batch_idx * batch_size
end = min((batch_idx + 1) * batch_size, num_samples)
i_batch = i_shuffled[start:end]
j_batch = j_shuffled[start:end]
log_co_batch = log_co_shuffled[start:end]
weights_batch = weights_shuffled[start:end]
optimizer.zero_grad()
loss = model(i_batch, j_batch, log_co_batch, weights_batch)
loss.backward()
optimizer.step()
total_loss += loss.item()
avg_loss = total_loss / num_batches
if (epoch + 1) % 10 == 0:
print(f"Epoch {epoch + 1}/{epochs}, Loss: {avg_loss:.4f}")
print("训练完成!")
# 使用示例
if __name__ == "__main__":
print("GloVe模型实现示例")
# 模拟数据
vocab_size = 5000
embedding_dim = 50
# 创建模型
model = GloVeModel(vocab_size, embedding_dim)
print(f"模型参数数量: {sum(p.numel() for p in model.parameters())}")
max
∣∣vb−va+vc∣∣⋅∣∣vd∣∣(vb−v
∣∣vw1∣∣⋅∣∣vw2∣∣vw1⋅v
if all(w in vocab for w in [a, b, c, d]):
# 计算 b - a + c
vec_a = word_vectors[vocab[a]]
vec_b = word_vectors[vocab[b]]
vec_c = word_vectors[vocab[c]]
target_vec = vec_b - vec_a + vec_c
# 计算与所有词的相似度
similarities = np.dot(word_vectors, target_vec)
similarities /= (np.linalg.norm(word_vectors, axis=1) * np.linalg.norm(target_vec))
# 排除输入词
for exclude_word in [a, b, c]:
similarities[vocab[exclude_word]] = -np.inf
# 找出最相似的词
predicted_idx = np.argmax(similarities)
predicted_word = list(vocab.keys())[list(vocab.values()).index(predicted_idx)]
if predicted_word == d:
correct += 1
total += 1
return correct / total if total > 0 else 0
def evaluate_similarity(word_vectors, vocab, test_pairs):
"""
评估词相似度任务
Args:
word_vectors: 词向量矩阵
vocab: 词到索引的字典
test_pairs: [(word1, word2, human_score)] 测试对
Returns:
Spearman相关系数
"""
model_scores = []
human_scores = []
for word1, word2, human_score in test_pairs:
if word1 in vocab and word2 in vocab:
vec1 = word_vectors[vocab[word1]]
vec2 = word_vectors[vocab[word2]]
# 计算余弦相似度
cos_sim = np.dot(vec1, vec2) / (np.linalg.norm(vec1) * np.linalg.norm(vec2))
model_scores.append(cos_sim)
human_scores.append(human_score)
# 计算Spearman相关系数
correlation, p_value = spearmanr(model_scores, human_scores)
return correlation
)
Xij<xmax Xij≥xmax
比较分层Softmax和负采样两种方法的优缺点。在什么情况下应该选择哪种方法?
推导负采样目标函数对上下文词向量 uo 和负样本词向量 uwi 的梯度。
证明GloVe的目标函数是凸函数还是非凸函数。如果是非凸的,讨论可能存在的局部最优问题。
推导sigmoid函数 σ(x)=1+e−x1 的导数,并证明:
~
k
)
a
+
)T
w2

