3 / 15

神经网络知识回顾 - 从感知机到深度网络 | 自在学

神经网络知识回顾

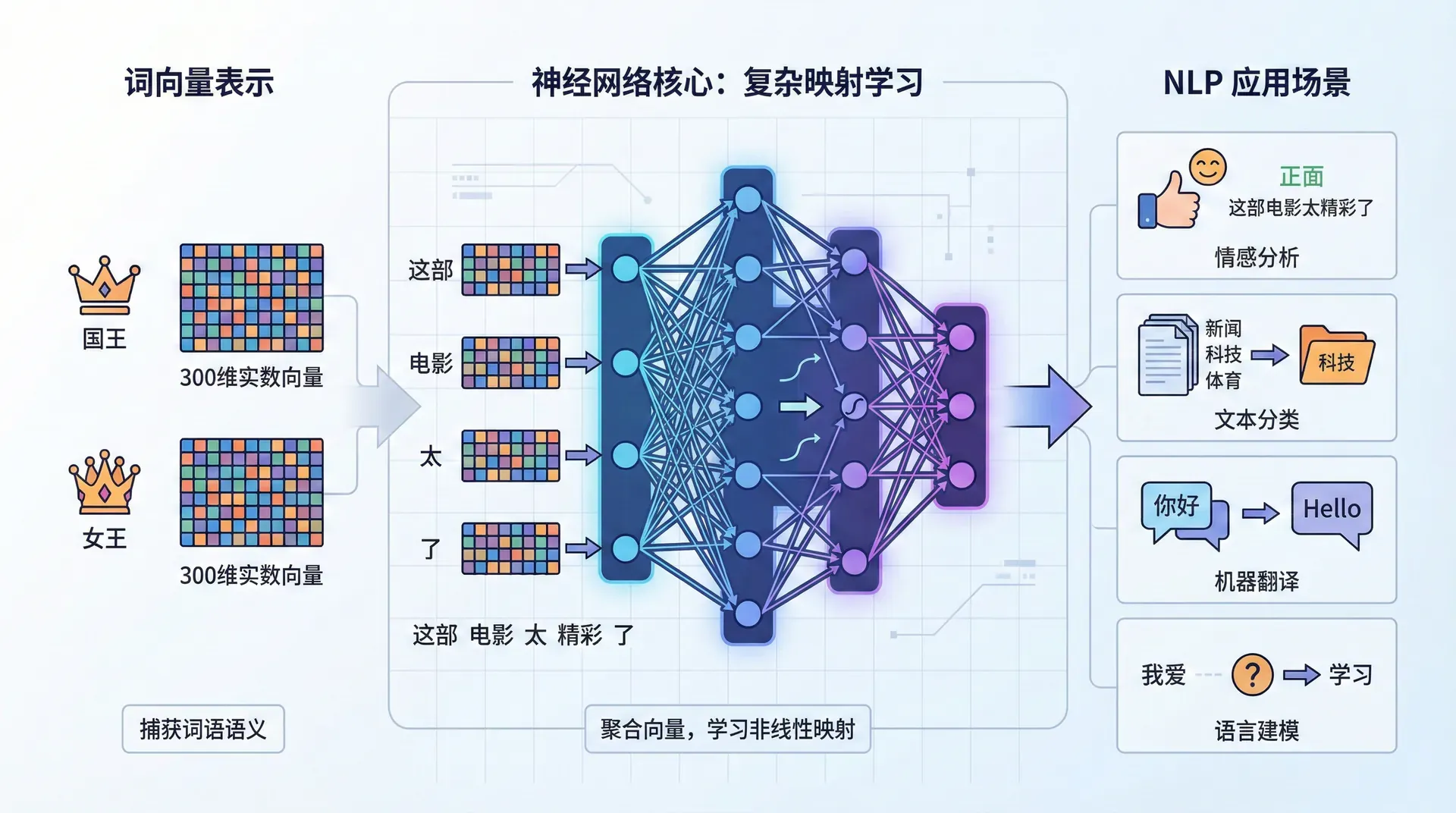
在前面两节课中，我们学习了如何将词语表示为密集的实数向量——Word2Vec让我们能够用300维向量捕获“国王”、“女王”这些词的语义。但仅有词向量还远远不够。如果你要构建一个情感分析系统，判断“这部电影太精彩了”是正面还是负面。你有了每个词的向量表示，但如何将这些向量组合起来，理解整个句子的情感？如何学习从“词向量序列”到“情感标签”的映射？

这正是神经网络要解决的问题——学习从输入到输出的复杂非线性映射。神经网络是现代深度学习的基础，在NLP领域几乎无处不在：文本分类需要神经网络聚合词向量；序列标注需要神经网络捕获上下文信息；机器翻译需要神经网络将源语言序列转换为目标语言序列；语言建模需要神经网络预测下一个词。

神经网络

从感知机到多层网络

感知机：神经网络的起点

故事要从1958年Frank Rosenblatt发明的**感知机（Perceptron）**说起。感知机是最简单的神经网络单元，可以看作一个线性分类器：

y = f\left(\sum_{i=1}^{n} w_i x_i + b\right) = f(\vec{w}^T \vec{x} + b)

这个公式虽然简单，却蕴含了深刻的思想。输入 $\vec{x}$ 是特征向量（如一个词的词向量），权重 $\vec{w}$ 决定了每个特征的重要性，偏置 $b$ 控制了决策边界的位置，激活函数引入非线性。

从几何角度看，感知机在特征空间中定义了一个超平面 $\vec{w}^T \vec{x} + b = 0$ ，将空间分为两部分。超平面一侧的点被分类为正类（），另一侧为负类（）。这就像在平面上画一条直线，把红点和蓝点分开。

但感知机有一个根本局限：它只能解决线性可分问题。最著名的反例是XOR问题——四个点 $(0,0), (0,1), (1,0), (1,1)$ ，前两个标签为0，后两个为1。无论如何画直线，都无法将它们分开。Marvin Minsky和Seymour Papert在1969年的书《Perceptrons》中严格证明了单层感知机无法解决XOR问题，这一度让神经网络研究陷入低谷（史称“AI冬天”）。

多层感知机：非线性的力量

1986年，Rumelhart、Hinton和Williams发表了反向传播算法，证明多层神经网络可以学习非线性决策边界，这彻底改变了格局。通过堆叠多层感知机，网络能够学习复杂的特征组合。

一个标准的多层前馈神经网络包含：

输入层：接收原始特征（如词向量）
隐藏层：一层或多层，进行非线性变换，提取高层特征
输出层：产生最终预测（如情感标签概率）

以两层神经网络为例：

\vec{h} = f^{(1)}(W^{(1)} \vec{x} + \vec{b}^{(1)})

\vec{y} = f^{(2)}(W^{(2)} \vec{h} + \vec{b}^{(2)})

第一层将输入 $\vec{x}$ （维度 $d_{in}$ ）通过权重矩阵 $W^{(1)}$ （维度）和激活函数映射到隐藏表示（维度）。第二层将映射到输出（维度）。

这种层次化的变换为什么有效？直觉上，每一层学习不同层次的特征。在图像识别中，第一层学习边缘、第二层学习纹理、第三层学习部件、第四层学习物体。在NLP中，第一层可能学习词的简单组合（如"not bad"），第二层学习短语结构，第三层学习句子级语义。通过层层抽象，网络能够从低层特征（词向量）构建高层理解（句子情感）。

通用逼近定理：理论保证

神经网络的强大不是经验性的，而是有严格数学保证的。Cybenko（1989）和Hornik（1991）证明了通用逼近定理：

定理：具有单个隐藏层且足够多神经元的前馈神经网络可以以任意精度逼近任意连续函数。

数学上，对于任意连续函数 $g: [0, 1]^n \rightarrow \mathbb{R}$ 和任意精度 $\epsilon > 0$ ，存在一个单隐藏层神经网络 $f$ ，使得：

\sup_{\vec{x} \in [0,1]^n} |f(\vec{x}) - g(\vec{x})| < \epsilon

这个定理从理论上保证了神经网络强大的表示能力——只要有足够多神经元，单层网络就能拟合任何函数！

但理论和实践有差距。定理保证了存在性，却没说如何找到这样的网络，也没说需要多少神经元。实践中，深层网络（多个隐藏层）通常比宽浅网络更有效——同样的参数量，深网络比浅网络性能更好。这是因为深层结构能够通过组合学习层次化特征，而宽浅网络只能学习“平坦”的特征。

激活函数

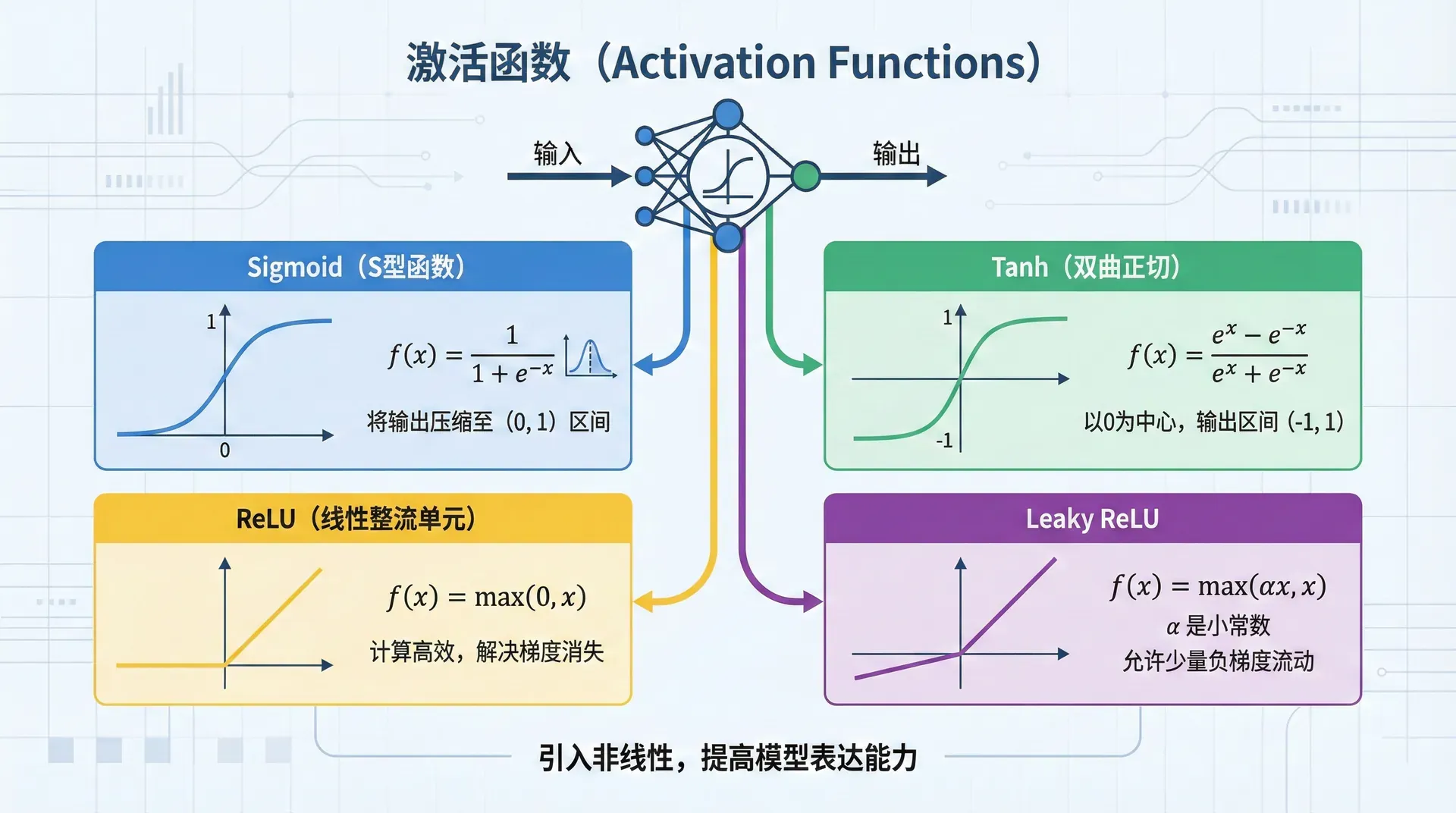
激活函数引入非线性，是神经网络能够学习复杂函数的关键。如果没有激活函数（或使用线性激活函数），多层网络等价于单层——无论堆叠多少层，最终都是输入的线性变换。激活函数打破了这个局限。

激活函数

Sigmoid：神经网络的老兵

Sigmoid函数是最早使用的激活函数之一：

\sigma(z) = \frac{1}{1 + e^{-z}}

它将任意实数映射到 $(0, 1)$ 区间，曲线呈S形。Sigmoid的优点是输出可以解释为概率（在0和1之间），而且平滑可微，导数为 $\sigma'(z) = \sigma(z)(1 - \sigma(z))$ ——这个简洁的形式让反向传播计算高效。

但Sigmoid有严重问题。梯度消失是最致命的：当 $|z|$ 很大时（如 $z=10$ 或 $z=-10$ ），sigmoid曲线变得非常平坦，导数 $\sigma'(z)$ 接近0。在反向传播中，梯度会通过链式法则连乘这些接近0的导数，经过多层后梯度变得极其微小，接近0——这就是梯度消失。结果是深层网络很难训练，底层的权重几乎不更新。

Sigmoid还有其他问题：输出不以零为中心（总是正数），可能导致梯度更新的方向问题；指数运算计算开销相对较大。因此，Sigmoid在隐藏层已经很少使用，主要用于输出层（二分类问题）和门控机制（LSTM中的门）。

Tanh：改进的S形函数

Tanh函数可以看作Sigmoid的改进版：

\tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}} = 2\sigma(2z) - 1

它将输入映射到 $(-1, 1)$ ，以零为中心，这解决了Sigmoid的"非零中心"问题。导数为 $\tanh'(z) = 1 - \tanh^2(z)$ ，在时达到最大值1。

Tanh在隐藏层比Sigmoid效果更好，因为零中心的输出让梯度更新更均衡。但它仍然存在梯度消失问题——当 $|z|$ 很大时， $\tanh'(z)$ 也接近0。在深度网络中，这个问题仍然会累积。

ReLU：深度学习的转折点

2011年，Krizhevsky等人在ImageNet竞赛上使用的AlexNet采用了ReLU（Rectified Linear Unit） 激活函数，效果惊人。ReLU的定义极其简单：

\text{ReLU}(z) = \max(0, z) = \begin{cases} z & \text{if } z > 0 \\ 0 & \text{if } z \leq 0 \end{cases}

这个简单的函数为什么革命性？首先，它大大缓解了梯度消失——当 $z > 0$ 时，导数恒为1，梯度可以无损地回传。其次，计算极快——只需要一个max操作，没有指数运算。第三，它引入了稀疏性——约50%的神经元输出为0，这种稀疏激活类似于生物神经元的工作方式，能够学习更鲁棒的特征。

但ReLU也有问题。Dead ReLU 现象：如果一个神经元的输入总是负数，那么它的输出永远是0，梯度永远是0，这个神经元就“死”了，无法再更新。这通常由不当的初始化或过大的学习率引起。

为了解决这个问题，研究者提出了多种ReLU变体：

Leaky ReLU给负数区域一个小斜率：

\text{LeakyReLU}(z) = \max(\alpha z, z), \quad \alpha \approx 0.01

这样即使 $z<0$ ，梯度也不为0，神经元不会完全死亡。

**ELU（Exponential Linear Unit）**在负数区域使用指数：

\text{ELU}(z) = \begin{cases} z & \text{if } z > 0 \\ \alpha(e^z - 1) & \text{if } z \leq 0 \end{cases}

ELU的输出均值接近零，能够加速学习，但计算成本比ReLU高。

实践建议：隐藏层默认使用ReLU，如果遇到Dead ReLU问题再尝试Leaky ReLU或ELU。输出层根据任务选择：二分类用Sigmoid，多分类用Softmax，回归不用激活函数。

损失函数

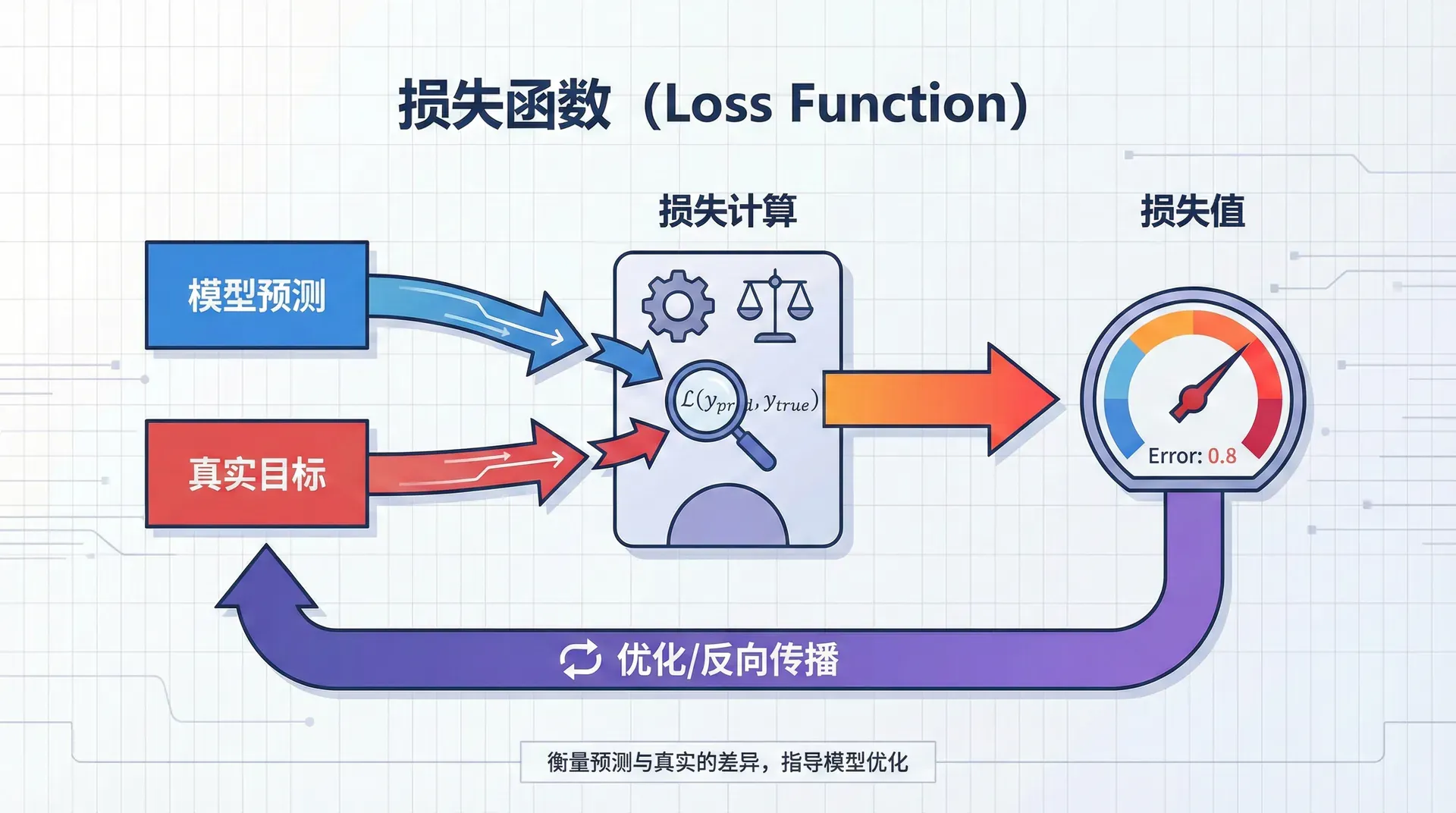
损失函数定义了“什么是好的预测”，是优化的目标。不同任务需要不同的损失函数。

损失函数

回归任务：均方误差

对于回归问题（预测连续值），**均方误差（Mean Squared Error, MSE）**是标准选择：

\mathcal{L}_{\text{MSE}} = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2

MSE惩罚预测值和真实值之间的平方差。为什么用平方而非绝对值？因为平方让大误差受到更重的惩罚（如误差10的惩罚是误差1的100倍），而且平方函数处处可微，便于梯度优化。MSE对应于假设误差服从高斯分布的最大似然估计。

分类任务：交叉熵

对于分类问题，**交叉熵损失（Cross-Entropy Loss）**是更好的选择。对于二分类：

\mathcal{L}_{\text{CE}} = -\frac{1}{N} \sum_{i=1}^{N} [y_i \log \hat{y}_i + (1 - y_i) \log(1 - \hat{y}_i)]

这里 $y_i \in \{0, 1\}$ 是真实标签， $\hat{y}_i \in (0,1)$ 是模型预测的概率。交叉熵来自信息论，度量两个概率分布的差异。

对于多分类（ $C$ 个类别），使用softmax和交叉熵的组合：

\hat{\vec{y}} = \text{softmax}(\vec{z}) = \frac{[\exp(z_1), \ldots, \exp(z_C)]}{\sum_{j=1}^{C} \exp(z_j)}

\mathcal{L}_{\text{CE}} = -\frac{1}{N} \sum_{i=1}^{N} \sum_{c=1}^{C} y_{i,c} \log \hat{y}_{i,c}

Softmax确保输出是有效的概率分布（非负且和为1），交叉熵惩罚模型对正确类别的低概率预测。

为什么分类用交叉熵而非MSE？ 交叉熵的梯度更合理。对于softmax+交叉熵，对输出 $z_c$ 的梯度是 $\hat{y}_c - y_c$ ——预测概率与真实概率的差。而MSE的梯度包含项（如果用sigmoid），当预测错误严重时，可能很小，导致学习缓慢。交叉熵没有这个问题，即使预测很错，梯度仍然大，学习快。

优化算法

有了损失函数，下一步是优化——找到让损失最小的权重。

优化算法

梯度下降

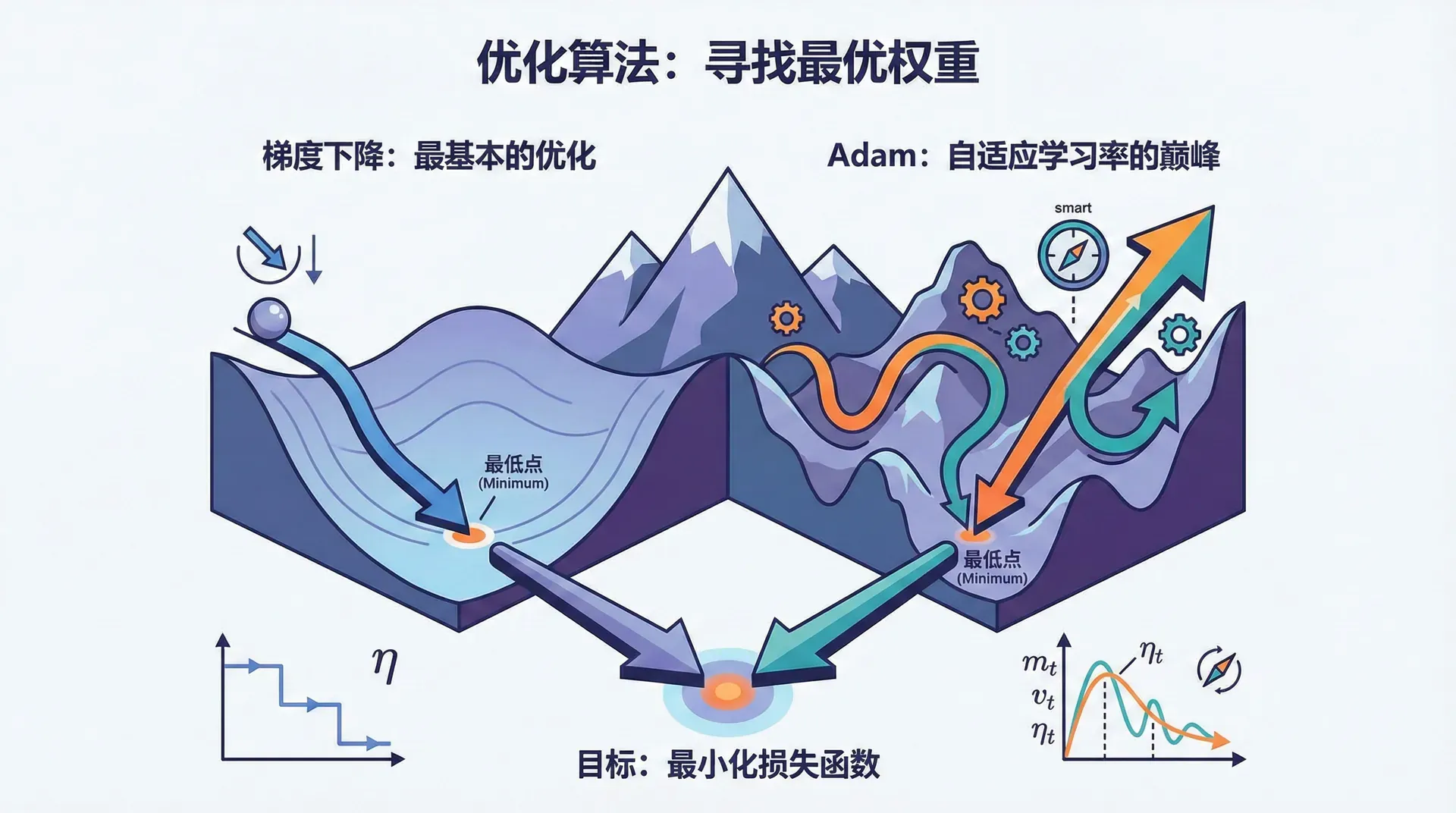
梯度下降（Gradient Descent, GD） 基于一个简单的思想：损失函数在某点的梯度指向损失增加最快的方向，那么负梯度就是损失减少最快的方向。沿着负梯度方向更新参数：

\vec{\theta}_{t+1} = \vec{\theta}_t - \eta \nabla_{\theta} \mathcal{L}(\vec{\theta}_t)

学习率 $\eta$ 控制步长。过小则收敛慢，过大则可能震荡甚至发散。

批量梯度下降（Batch GD） 在整个数据集上计算梯度。优点是梯度准确，收敛稳定；缺点是计算慢，内存开销大，对于大数据集不实用。

随机梯度下降（SGD） 每次只用一个样本计算梯度，更新频繁。优点是快，能在线学习；缺点是梯度有噪声，更新不稳定。

小批量梯度下降（Mini-batch GD） 是折中：每次用一小批样本（如32、64、128）计算梯度。这是实践中的标准选择——既利用了硬件的并行计算能力，又保持了合理的更新频率。

Adam

实践中，最常用的优化器不是朴素SGD，而是Adam（Adaptive Moment Estimation）。Adam结合了两个关键思想：

动量（Momentum）：利用历史梯度的指数移动平均，加速收敛并减少震荡：

\vec{m}_t = \beta_1 \vec{m}_{t-1} + (1 - \beta_1) \nabla_{\theta} \mathcal{L}(\vec{\theta}_t)

自适应学习率：为每个参数维度维护单独的学习率，基于梯度平方的指数移动平均：

\vec{v}_t = \beta_2 \vec{v}_{t-1} + (1 - \beta_2) (\nabla_{\theta} \mathcal{L}(\vec{\theta}_t))^2

然后进行偏差修正和参数更新：

\hat{\vec{m}}_t = \frac{\vec{m}_t}{1 - \beta_1^t}, \quad \hat{\vec{v}}_t = \frac{\vec{v}_t}{1 - \beta_2^t}

\vec{\theta}_{t+1} = \vec{\theta}_t - \eta \frac{\hat{\vec{m}}_t}{\sqrt{\hat{\vec{v}}_t} + \epsilon}

Adam的优点是对学习率不敏感，收敛快，适用范围广。默认超参数（ $\beta_1=0.9$ , $\beta_2=0.999$ , $\epsilon=10^{-8}$ ）在大多数任务上表现良好，是NLP的首选优化器。

正则化

深度网络参数众多，容易过拟合——在训练集上表现完美，但泛化能力差。正则化技术通过约束模型复杂度，提升泛化能力。

Dropout

Dropout（Hinton et al., 2012）是最有效的正则化技术之一。训练时，每个神经元以概率 $p$ （通常0.5）被随机"关闭"（输出置为0）。测试时，所有神经元都激活，但输出乘以 $p$ （或训练时除以 $1-p$ ，等价）。

为什么Dropout有效？直觉上，它强迫网络学习鲁棒的特征——因为任何神经元都可能被随机关闭，网络不能过度依赖某些特定神经元，必须学习分布式的、冗余的表示。数学上，Dropout可以看作训练指数级多个子网络的集成，测试时对它们的预测取平均。

其他正则化技术

L2正则化（权重衰减） 在损失函数中添加权重的平方和：

\mathcal{L}_{\text{total}} = \mathcal{L}_{\text{data}} + \frac{\lambda}{2} \|\vec{\theta}\|^2

这鼓励权重保持小值，防止某些权重过大导致的过拟合。

Early Stopping：监控验证集性能，当性能不再提升时停止训练，避免过度拟合训练集。

Batch Normalization：归一化每层的输入，使其均值为0、方差为1，加速训练并起到正则化作用。

实践技巧

权重初始化

不当的初始化可能导致梯度消失/爆炸，让网络无法训练。Xavier初始化（Glorot & Bengio, 2010）从均匀分布采样：

W \sim U\left(-\sqrt{\frac{6}{n_{in} + n_{out}}}, \sqrt{\frac{6}{n_{in} + n_{out}}}\right)

对于ReLU，He初始化（He et al., 2015）更好：

W \sim N\left(0, \sqrt{\frac{2}{n_{in}}}\right)

PyTorch的nn.Linear默认使用合理的初始化，通常不需要手动设置。

学习率调度

固定学习率可能不是最优的。学习率衰减：训练初期用大学习率快速接近最优点，后期用小学习率精细调整。常见策略包括阶梯衰减、指数衰减、余弦退火等。

梯度裁剪

训练RNN时，梯度爆炸是常见问题。梯度裁剪限制梯度的范数：

|
torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=5.0)

这确保梯度不会过大，稳定训练。

PyTorch实现：文本分类示例

让我们用PyTorch实现一个简单的文本分类器，综合应用我们到目前为止学到的所有知识：

|
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
 
class TextClassifier(nn.Module):
    """简单的文本分类器"""
    
    def __init__(self, vocab_size, embedding_dim, hidden_dim, output_dim, 
                 dropout=0.5):
        super(TextClassifier, self).__init__()

这个示例展示了完整的训练流程：定义模型、设置优化器和损失函数、训练和评估循环、梯度裁剪、准确率统计等。虽然这个模型很简单（只用平均池化聚合词向量），但它体现了神经网络训练的核心流程。

练习与思考

解释为什么没有激活函数（或使用线性激活函数），多层神经网络等价于单层网络。
证明Sigmoid函数的导数 $\sigma'(z) = \sigma(z)(1 - \sigma(z))$ 。利用这个结果，分析为什么Sigmoid会导致梯度消失。
在一个三层神经网络中，如果每层的梯度都是0.1，经过反向传播后输入层的梯度是多少？如果换成ReLU（导数为1），结果如何？
实现一个包含Batch Normalization的神经网络，比较有无BN对训练速度和最终性能的影响。
为什么分类任务用交叉熵而非MSE？用一个具体例子说明MSE在分类任务上的问题。

z=0