二叉搜索树
在基础数据结构之上,我们现在来了解一下一个特殊的树结构,它能高效地支持动态集合的全部字典操作:SEARCH, MINIMUM, MAXIMUM, PREDECESSOR, SUCCESSOR, INSERT 和 DELETE。这种结构就是二叉搜索树(Binary Search Tree, BST)。
二叉搜索树上所有基本操作的时间复杂度都与树的高度 成正比,即 。对于一个包含 个节点的随机创建的二叉搜索树,其期望高度为 ,因此平均性能非常出色。 然而,在最坏情况下,它可能退化成一条长度为 的链,此时性能会降至 。在后续部分,我们还会学习红黑树等高级结构,它们通过特定的约束来保证树的高度始终维持在 ,从而确保了操作的最坏情况性能。
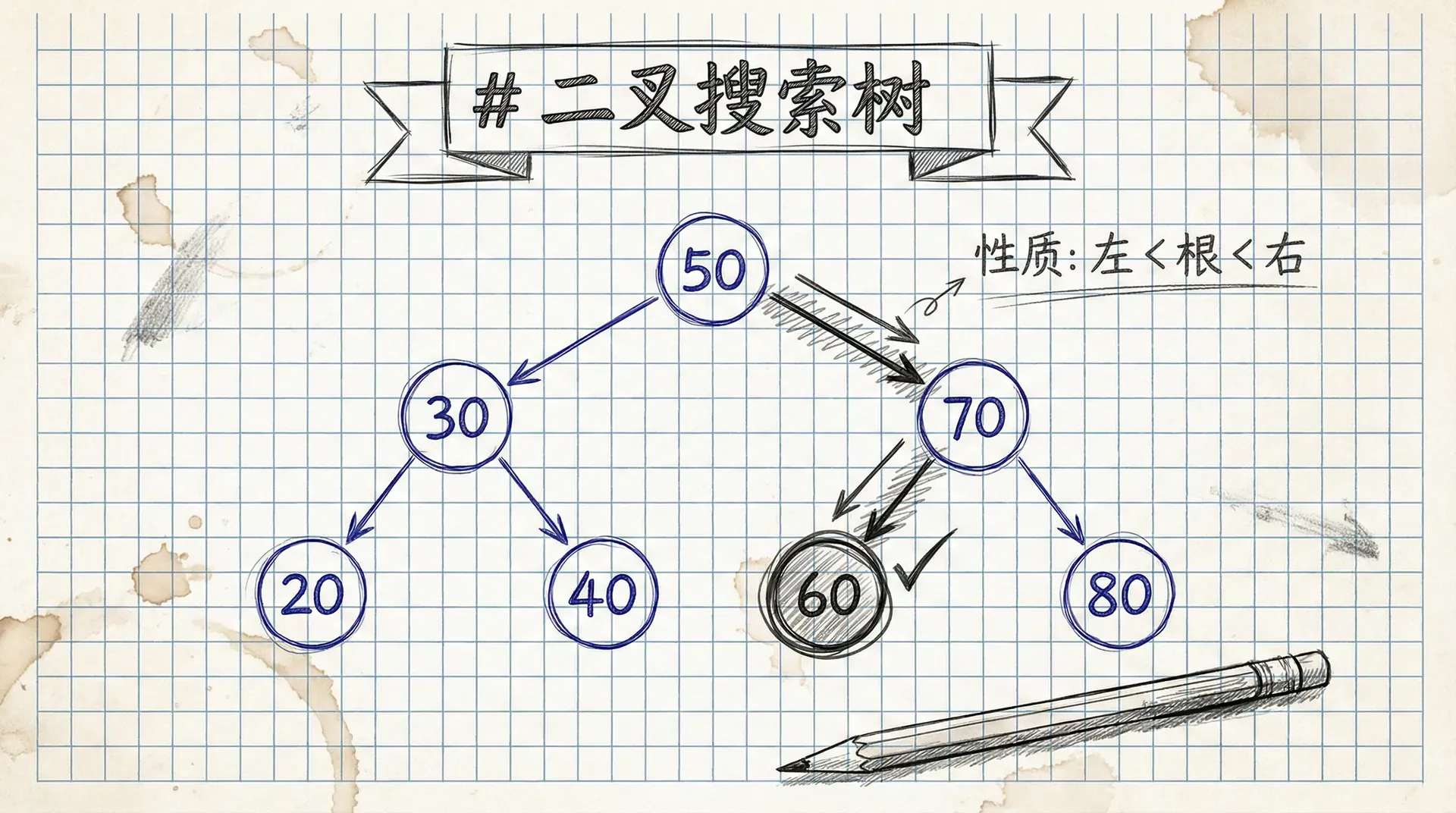
什么是二叉搜索树?
顾名思义,二叉搜索树是一棵二叉树,但它额外满足一个重要的性质,对于树中的任意节点 x:
- 其左子树中的所有节点的键值,都小于或等于
x的键值。 - 其右子树中的所有节点的键值,都大于或等于
x的键值。
这个性质是二叉搜索树所有操作的基础。它保证了我们可以通过比较键值来快速地缩小搜索范围。
中序遍历
二叉搜索树有一个不错的特性,那就是通过一种称为**中序遍历(Inorder Tree Walk)**的方法,我们能够以从小到大的顺序,逐一访问并打印出树中所有节点的键值。 这种遍历方式不仅让我们能够轻松获取所有节点的信息,还能保证这些信息是按顺序排列的,就像在图书馆中找到一本书时,我们总是能在正确的位置找到它。
|INORDER-TREE-WALK(x) if x != NIL INORDER-TREE-WALK(x.left) print x.key INORDER-TREE-WALK(x.right)
这个递归过程保证了先访问左子树(所有较小的值),再访问根节点,最后访问右子树(所有较大的值),从而得到一个有序的序列。对于一棵有 个节点的树,中序遍历的时间复杂度为 。
查询二叉搜索树
查找元素
TREE-SEARCH(x, k) 从根节点 x 开始,查找键值为 k 的节点。
如果 k 等于当前节点的键值,查找成功。
如果 k 小于当前节点的键值,则在左子树中继续查找。
如果 k 大于当前节点的键值,则在右子树中继续查找。
查找最大/最小值
- 最小值:从根节点开始,一直沿着左子节点的指针走,直到尽头,最后一个节点就是最小值所在。
- 最大值:从根节点开始,一直沿着右子节点的指针走,直到尽头。
查找后继与前驱
-
后继(Successor):一个节点
x的后继,是在中序遍历中紧跟在x后面的那个节点。- 如果
x有右子树,那么它的后继就是其右子树中的最小值。 - 如果
x没有右子树,那么它的后继是其“最低的、且x在其左子树中的那个祖先”。
- 如果
-
前驱(Predecessor):与后继对称。
- 如果
x有左子树,那么它的前驱就是其左子树中的最大值。 - 如果
x没有左子树,那么它的前驱是其“最低的、且x在其右子树中的那个祖先”。
- 如果
上述操作的时间复杂度都是 。
插入与删除
插入
TREE-INSERT(T, z) 的过程与搜索类似。我们从根节点开始,沿着一条路径向下,为新节点 z 寻找一个合适的空位(NIL),然后将 z 插入。这个过程同样是 的。
|TREE-INSERT(T, z) y = NIL x = T.root while x != NIL y = x if z.key < x.key x = x.left else x = x.right z.p = y if y == NIL T.root = z // tree T was empty
删除
TREE-DELETE(T, z) 是所有操作中最复杂的一个,需要分情况讨论。为了简化代码,我们通常会定义一个辅助过程 TRANSPLANT(T, u, v),它用以 v 为根的子树来替换以 u 为根的子树。
删除操作的三个核心情况:
z是叶子节点:直接删除z,并修改其父节点的指针。z只有一个子节点:将z的子节点“提拔”到z的位置,替换z。z有两个子节点:这是最复杂的情况。- 首先,找到
z的后继y(y一定在z的右子树中,并且y本身没有左子节点)。 - 用
y来替换z在树中的位置。这个过程又分为两种子情况:- 如果
y就是z的右孩子,直接用y替换z。 - 如果
y不是z的右孩子,那么先用y的右孩子替换y自身的位置,然后再用y替换z。
- 如果
- 首先,找到
整个删除操作的时间复杂度也是 。
操作可视化
随机建立的二叉搜索树
我们已经看到,二叉搜索树的所有基本操作,其运行时间都与树的高度 成正比。如果树是平衡的,则 ,性能很好;如果树是不平衡的,退化成一条链,则 ,性能很差。
那么,一个“典型”的二叉搜索树是怎样的呢?如果我们向一棵空树中,按随机顺序插入 个不同的键,所形成的随机建立的二叉搜索树(Randomly Built Binary Search Tree),其性质如何?
一个有 个不同键的随机建立的二叉搜索树,其期望高度为 。
尽管存在最坏情况,但平均来看,二叉搜索树的性能是很好的。这个结论的证明比较复杂,涉及到对树高和节点秩的概率分析,但其核心思想与快速排序的平均情况分析是相通的:随机的插入顺序,使得产生极度不平衡树的概率非常小。大多数情况下,树的形态会趋向于平衡。
虽然我们不能总保证输入是随机的,但这个定理给了我们一个重要的启示:如果输入的顺序可能导致最坏情况,我们可以通过在插入前随机打乱输入序列,来构造一棵期望高度为 的树,从而在平均意义上获得良好的性能。这与随机化快速排序的思想异曲同工。
小练习
给定以下二叉搜索树:
-
请回答以下问题:
- 执行
TREE-SEARCH(T, 7)的搜索路径是什么? - 执行
TREE-SEARCH(T, 16)的搜索路径是什么? - 插入节点 13 后,树的结构会变成什么样?
- 删除节点 6 后,树的结构会变成什么样?
- 执行
-
遍历顺序: 对于上面的二叉搜索树,请写出:
- 中序遍历的结果
- 前序遍历的结果
- 后序遍历的结果
-
时间复杂度分析: 分析以下操作在最坏情况下的时间复杂度:
- 在平衡的二叉搜索树中搜索一个元素
- 在退化成链表的二叉搜索树中搜索一个元素
- 在随机建立的二叉搜索树中搜索一个元素
-
算法实现: 实现以下函数(也可以用你熟悉的语言):
|def find_minimum(root): """找到二叉搜索树中的最小节点""" pass def find_maximum(root): """找到二叉搜索树中的最大节点""" pass def find_successor(node): """找到给定节点的后继节点""" pass def find_predecessor(node): """找到给定节点的前驱节点""" pass
-
树的构建: 给定序列
[15, 6, 18, 3, 7, 17, 20, 2, 4, 13, 9]:- 按照给定顺序插入节点,画出最终的二叉搜索树
- 计算树的高度
- 计算树中所有节点的深度之和
-
删除操作分析,对于以下二叉搜索树分析删除以下节点时会发生什么:
- 删除节点 3(叶子节点)
- 删除节点 7(只有一个子节点)
- 删除节点 10(有两个子节点)