红黑树

在前面的部分中，我们深入探讨了二叉搜索树（Binary Search Tree, BST）。我们发现 BST 是一种极为高效的数据结构，它在理想情况下能够将查找、插入和删除等操作的时间复杂度维持在令人惊叹的 $O(\log n)$ 水平。这种对数时间的性能源于其核心特性：对于树中的任意节点 $x$ ，其左子树中所有节点的值均小于或等于 $x$ 的值，而右子树中所有节点的值均大于或等于 $x$ 的值。这一特性使得我们每次比较都能排除大约一半的节点，从而实现了快速定位。

然而，二叉搜索树的卓越性能有一个致命的弱点——它严重依赖于树的“形态”或“结构”。当数据以一种相对随机的顺序插入时，我们很可能得到一棵大致平衡的树，其高度约等于 $\log_2 n$ ，从而保证了 $O(\log n)$ 的操作效率。但是，如果数据以一种有序或接近有序的方式插入，例如，我们按顺序插入数字 1, 2, 3, 4, 5，二叉搜索树就会退化成一个链表。

在上面右侧的退化情况下，树的高度不再是 $\log n$ ，而是 $n$ 。这意味着，在最坏的情况下，查找一个元素需要从根节点一直遍历到最深的叶子节点，操作的时间复杂度从 $O(\log n)$ 急剧恶化为 $O(n)$ 。这与在一个无序数组中进行线性搜索的效率相当，我们构建二叉搜索树所期望的性能优势荡然无存。对于需要处理大规模动态数据集的应用程序，例如数据库索引、操作系统任务调度或内存管理，这种性能上的不确定性是不可接受的。我们不能把系统的稳定性寄希望于输入数据的随机性。

为了解决这一根本性问题，计算机科学家们设计出了一系列“自平衡”的二叉搜索树。这些数据结构在标准的二叉搜索树的基础上，增加了一套精巧的规则和维护机制，确保在每次插入或删除操作后，树的高度始终保持在 $O(\log n)$ 的量级。无论输入数据的顺序如何，它们都能通过一系列局部调整（例如“旋转”操作）来防止树变得过于“倾斜”或“不平衡”。

红黑树

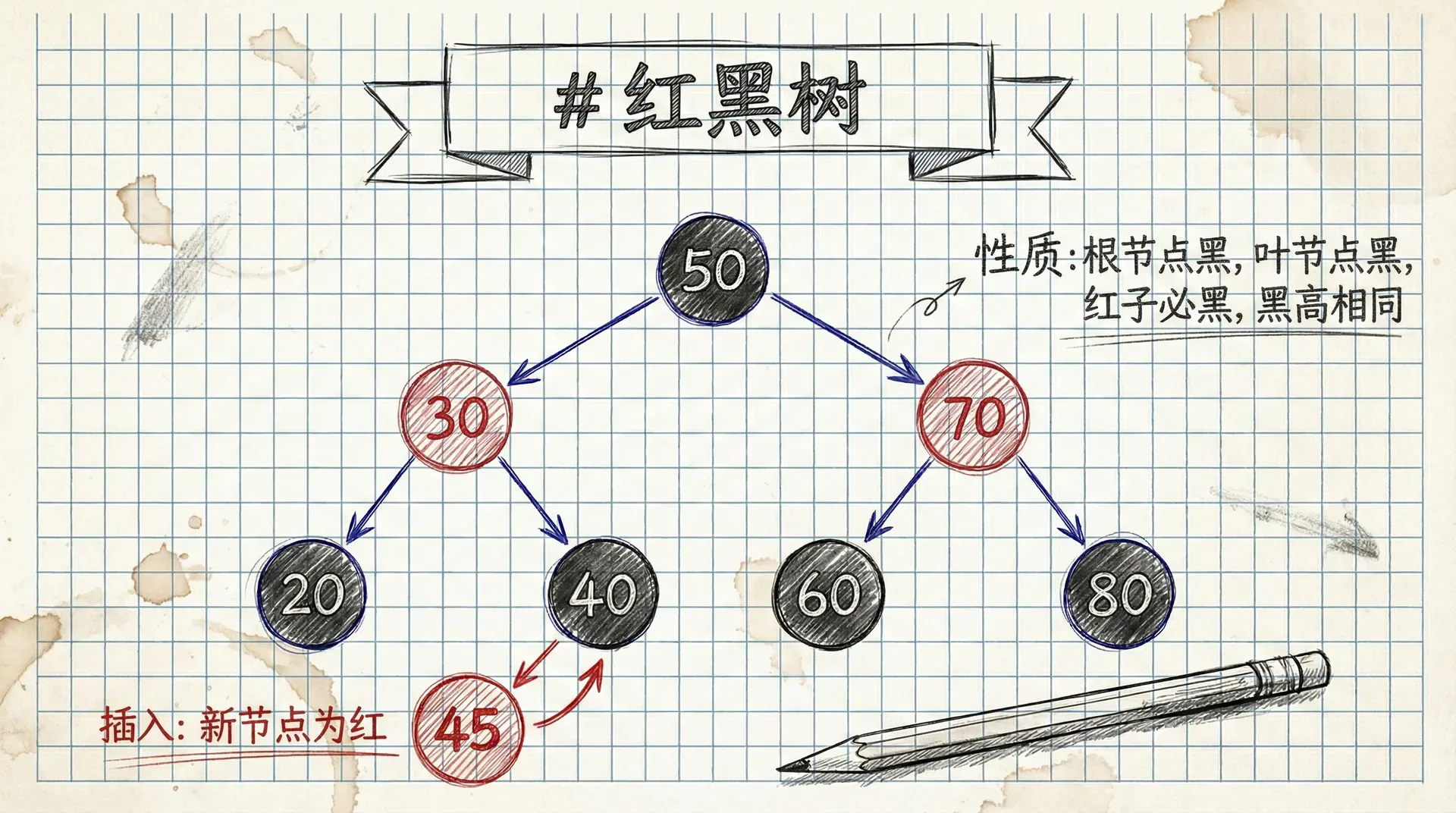
在本部分中，我们将学习其中最著名和应用最广泛的一种自平衡二叉搜索树——红黑树（Red-Black Tree）。红黑树在许多主流的软件库和系统中都扮演着核心角色，例如 C++ STL 中的 map 和 set，Java 中的 TreeMap 和 TreeSet，以及 Linux 内核中的内存管理和调度器。

红黑树的精妙之处在于，它通过为每个节点赋予“红色”或“黑色”的属性，并遵循一组简单的规则，巧妙地维持了树的近似平衡。这些规则确保了从根节点到最远叶子节点的任何路径，其长度都不会超过到最近叶子节点路径长度的两倍。这足以保证树的高度始终保持在 $O(\log n)$ ，从而为所有基本动态集合操作提供了最坏情况下的性能保证。

我们将从红黑树的基本性质入手，理解这些性质如何共同作用以维持平衡。然后，我们将详细剖析其核心维护操作——旋转，这是调整树结构而不破坏二叉搜索树性质的关键。最后，我们将一步步、抽丝剥茧地分析红黑树最复杂的部分：插入和删除操作。我们将看到，当插入或删除一个节点可能破坏红黑性质时，算法会如何通过一系列优雅的颜色变换和旋转操作，重新恢复树的平衡，确保性能的稳定。

红黑树的性质

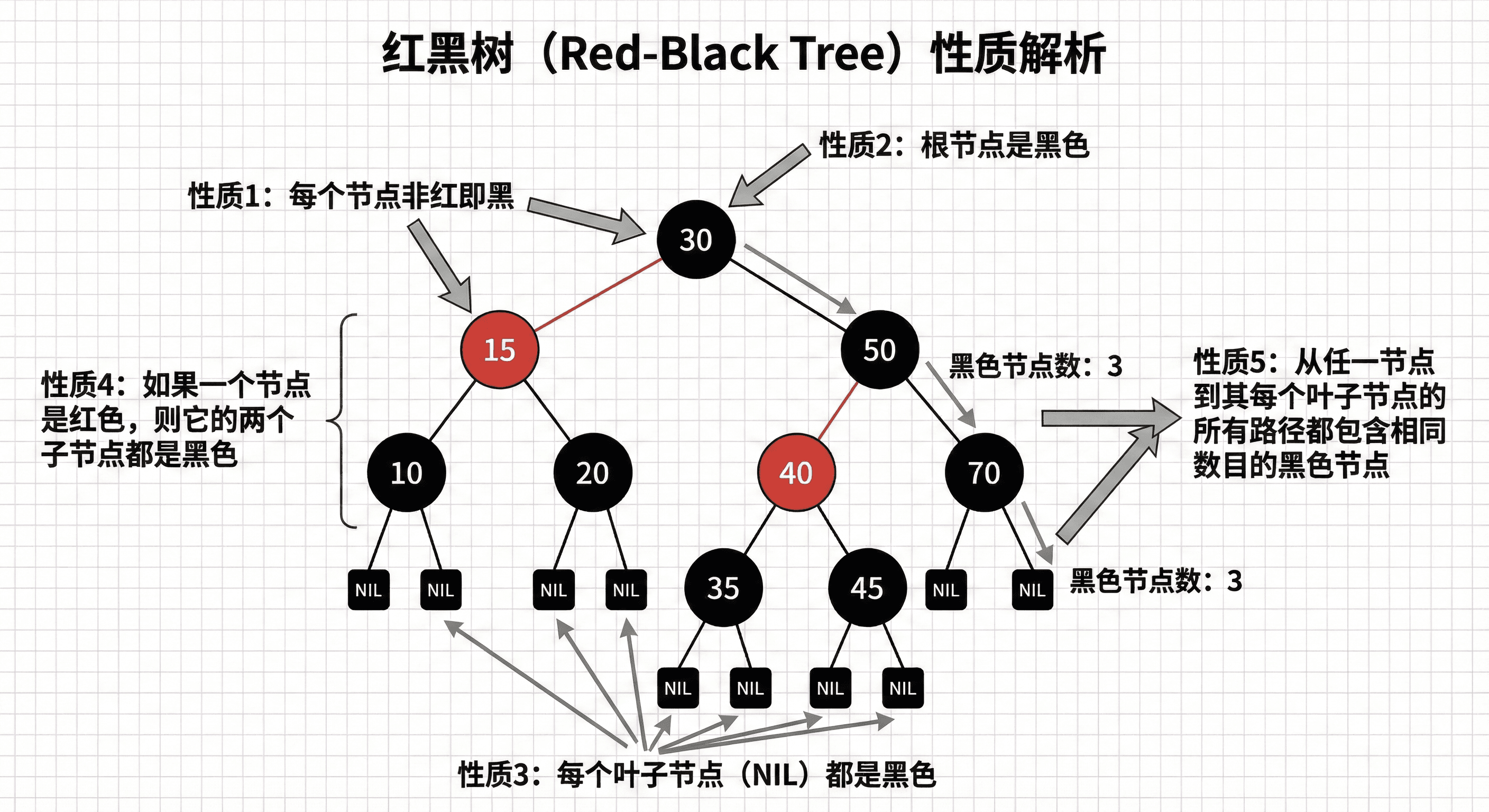
红黑树的本质是一棵二叉搜索树，但它在每个节点上增加了一个额外的存储位来表示节点的颜色，这个颜色可以是红色（RED）或黑色（BLACK）。通过对从根节点到叶子节点的任何路径上各个节点的颜色分布进行限制，红黑树确保了没有任何一条路径会比其他路径长出太多。这种巧妙的"近似平衡"策略，正是红黑树高效性能的根源。一棵标准的红黑树必须满足以下五个性质，这些性质是定义一棵树是否为"红黑树"的充要条件：

节点颜色性质 (Color Property): 每个节点要么是红色的，要么是黑色的。
根节点性质 (Root Property): 根节点是黑色的。
叶子节点性质 (Leaf Property): 每个叶子节点（NIL）是黑色的。
红色节点性质 (Red Property): 如果一个节点是红色的，则它的两个子节点都必须是黑色的。
黑色高度性质 (Black-Height Property): 对每个节点，从该节点到其所有后代叶子节点（NIL）的简单路径上，均包含相同数目的黑色节点。

这些性质，特别是第 4 和第 5 条，共同保证了一棵含有 $n$ 个内部节点的红黑树，其高度 $h$ 最大不会超过 $2 \log_2(n+1)$ 。这是一个非常重要的结论，它意味着树的高度始终是 $O(\log n)$ 。这个结论的直观理解如下：

根据性质 4，任何路径上红色节点不能相邻，所以黑色节点至少占一半。
根据性质 5，每条路径的黑色节点数量相等（我们称之为树的黑高 $bh$ ）。
考虑最短的路径：这条路径完全由黑色节点组成，其长度就是树的黑高 $bh$ 。
考虑最长的路径：由于红色节点不能相邻，这条路径最多是黑红交替的，即 B-R-B-R...。因此，其长度最多是 $2 \times bh$ 。

既然从根到叶子的最短路径长度至少是 $bh$ ，最长路径长度至多是 $2 \times bh$ ，这就意味着最长路径不会超过最短路径的两倍。这就从根本上杜绝了树变得像链表一样"细长"的可能性，保证了树的大致平衡。

旋转操作

在深入研究红黑树的插入和删除算法之前，我们必须先掌握一种能够修改树结构的基本工具——旋转（Rotation）。旋转是一种在二叉搜索树上进行的局部操作，它能够在不违反二叉搜索树性质的前提下，改变树中节点之间的父子关系。

旋转操作的核心目标是降低树中某一侧的高度，同时增加另一侧的高度，从而帮助我们重新平衡树的结构。这种操作对于维护红黑树的性质至关重要。当一次插入或删除导致红黑性质被破坏时，我们常常需要通过一次或多次旋转来重构树的局部拓扑，使其重新满足所有要求。

旋转分为两种基本类型：左旋（Left-Rotate） 和 右旋（Right-Rotate）。这两种操作是互为逆运算的。

左旋 (Left-Rotate)

假设我们要在节点 $x$ 上执行一次左旋操作。执行左旋的前提是， $x$ 的右子节点 $y$ 不能是 NIL 哨兵节点。左旋操作围绕连接 $x$ 和 $y$ 的"链"进行，可以形象地理解为"将 $y$ 向上提，同时将 $x$ 向下拉到 $y$ 的左侧"。下面是一个详细的操作步骤：

确定 y: 令 $y$ 为 $x$ 的右子节点。如前所述， $y$ 必须存在。

处理 y 的左子树 (β): $y$ 的左子树将成为 $x$ 的新的右子树。我们执行 x.right = y.left。如果 $y$ 的左子树存在（即 y.left != T.nil），我们还需要更新其父指针，使其指向 $x$ ，即 y.left.p = x。

更新 y 的父指针: $y$ 将取代 $x$ 在树中的位置。我们将 $x$ 的父节点 $p$ 赋给 $y$ 的父节点，即 y.p = x.p。

如果 $x$ 原本是根节点（x.p == T.nil），那么 $y$ 现在就成为新的根节点 (T.root = y)。
如果 $x$ 是其父节点的左孩子，那么 $y$ 就成为 $x$ 父节点的新的左孩子 (x.p.left = y)。
如果 $x$ 是其父节点的右孩子，那么 $y$ 就成为 $x$ 父节点的新的右孩子 (x.p.right = y)。

连接 x 和 y: 最后，我们将 $x$ 设置为 $y$ 的左孩子，y.left = x，并更新 $x$ 的父指针指向 $y$ ，x.p = y。

在上图中，我们可以看到左旋操作的核心变化：

节点 x（红色节点）从父节点的直接子节点变成了 y 的左子节点
节点 y（绿色节点）从 x 的右子节点变成了父节点的直接子节点
子树 β（y 的左子树）从 y 的左子树变成了 x 的右子树
子树 α 和 γ 的位置保持不变，只是它们的父节点关系发生了变化

伪代码实现：

LEFT-ROTATE(T, x)
    y = x.right                 # 步骤 1: 确定 y
    x.right = y.left            # 步骤 2: 将 y 的左子树 β 设为 x 的右子树
    if y.left != T.nil
        y.left.p = x
    y.p = x.p                     # 步骤 3: y 继承 x 的父节点
    if x.p == T.nil
        T.root = y
    else if x == x.p.left
        x.p.left = y
    else
        x.p.right = y
    y.left = x                    # 步骤 4: 将 x 设为 y 的左孩子
    x.p = y

右旋 (Right-Rotate)

右旋操作 RIGHT-ROTATE(T, y) 与左旋完全对称。它将节点 $y$ 向下拉，使其成为其原左孩子 $x$ 的右孩子。执行右旋的前提是， $y$ 的左子节点 $x$ 不能是 NIL。

伪代码实现：

RIGHT-ROTATE(T, y)
    x = y.left                  # 步骤 1: 确定 x
    y.left = x.right            # 步骤 2: 将 x 的右子树 β 设为 y 的左子树
    if x.right != T.nil
        x.right.p = y
    x.p = y.p                     # 步骤 3: x 继承 y 的父节点
    if y.p == T.nil
        T.root = x
    else if y == y.p.left
        y.p.left = x
    else
        y.p.right = x
    x.right = y                   # 步骤 4: 将 y 设为 x 的右孩子
    y.p = x

旋转操作的时间复杂度

无论是左旋还是右旋，算法都只涉及常数次指针的修改。它不会递归地深入树的其他部分，也不会遍历任何子树。因此，旋转操作本身的时间复杂度是 $O(1)$ 。

这种高效的、常数时间的结构调整能力，是红黑树能够在 $O(\log n)$ 时间内完成插入和删除操作的基础。当我们发现树的平衡被打破时，我们可以迅速地通过几次旋转来修复它，而旋转本身的开销极小。

插入操作

现在我们拥有了旋转这个强大的工具，可以开始探索红黑树的动态操作了。首先是插入。将一个新节点插入到红黑树中，同时要确保插入之后所有五个红黑性质依然被满足，这是一个精巧的过程。整个插入操作 RB-INSERT 可以分为两个主要阶段：

标准的二叉搜索树插入： 首先，我们忽略颜色，像在普通的二叉搜索树中一样，为新节点找到合适的位置并将其插入。

修复红黑性质： 插入新节点后，某些红黑性质可能会被破坏。我们需要一个修复程序，通过一系列的重新着色和旋转操作，来恢复这些性质。

RB-INSERT(T, z) 算法的概要：

使用一个指针 y (作为尾随指针) 和 x (作为遍历指针) 从根节点开始，按照二叉搜索树的规则向下查找，为新节点 z 找到一个合适的父节点 y。

将 z 作为 y 的孩子插入。

将新插入的节点 z 的左右孩子设为 T.nil。

将新节点 z 的颜色设置为红色。

调用一个辅助程序 RB-INSERT-FIXUP(T, z) 来解决可能由此引发的红黑性质冲突。

为什么将新节点涂成红色？。让我们分析一下，插入一个红色的新节点 z 会破坏哪些性质：

性质 1 (颜色): 满足，因为节点是红色或黑色。
性质 2 (根节点): 如果 z 是根节点，那么根是红色的，违反了此性质。但这很容易修复，只需在最后将根节点涂黑即可。
性质 3 (叶子): 满足，z 的叶子是黑色的 NIL 节点。
性质 4 (红色节点): 这是最可能被破坏的性质。如果 z 的父节点 p 也是红色的，那么我们就有了两个连续的红色节点，这被称为"红-红冲突"。
性质 5 (黑色高度): 这个性质一定会被满足！ 因为新插入的红色节点 z 不会改变任何路径上的黑色节点数量。所有路径的黑高都保持不变。

如果我们选择将新节点涂成黑色，性质 4 肯定不会被违反。但是，性质 5 几乎肯定会被破坏。因为将一个黑色的 z 插入后，包含 z 的路径会比其他路径多一个黑色节点，导致黑高不一致。修复黑高不一致的问题比修复红-红冲突要复杂得多。因此，选择将新节点涂成红色，并将修复的焦点放在可能出现的红-红冲突上，是更明智的策略。

`RB-INSERT-FIXUP`: 修复红-红冲突

RB-INSERT-FIXUP 的任务就是解决新插入的红色节点 z 可能与其父节点 z.p 发生的红-红冲突。它的核心逻辑是一个 while 循环，循环的条件是 z 的父节点 z.p 是红色的。只要这个条件成立，我们就知道性质 4 被违反了，需要进行处理。在循环的每次迭代中，我们关注的是 z、它的父节点 z.p 和它的祖父节点 z.p.p。我们还需要考虑 z 的"叔叔"节点，也就是 z.p 的兄弟节点。根据叔叔节点的颜色，我们分为三种主要情况来处理。为了方便讨论，我们假设 z 的父节点 z.p 是其祖父节点 z.p.p 的 左孩子。对于 z.p 是右孩子的情况，处理方式是完全对称的，我们稍后会提到。

情况 1: `z` 的叔叔节点是红色的

条件: z 的父节点 z.p 是红色的，且 z 的叔叔节点 y 也是红色的。

将 z 的父节点 z.p 涂成黑色。

将 z 的叔叔节点 y 涂成黑色。

将 z 的祖父节点 z.p.p 涂成红色。

将指针 z 移动到其祖父节点 z.p.p 上，即 z = z.p.p。

分析： 这个操作非常巧妙。通过将 z.p 和 y 变黑，z.p.p 变红，我们解决了 z 和 z.p 之间的红-红冲突。同时，由于 z.p 和 y 都从红色变成了黑色，任何通过 z.p 或 y 的路径，其黑色节点数量都增加了一。为了补偿这一点，我们将 z.p.p 从黑色变成红色，使得任何通过 z.p.p 的路径的黑色节点数量减少了一。这样一来，黑高性质（性质 5）得以保持！

然而，将祖父节点 z.p.p 涂成红色，可能会导致它与它的父节点（z 的曾祖父）产生新的红-红冲突。因此，我们需要将 z 指向 z.p.p，然后返回到 while 循环的开始，在新的 z 节点上继续检查和修复。问题被有效地"向上推"了两层。

情况 2: `z` 的叔叔是黑色，且 `z` 是一个右孩子 (形成三角关系)

将指针 z 移动到其父节点 z.p 上，即 z = z.p。

对新的 z (也就是旧的 z.p) 执行一次左旋操作。

分析： 情况 2 本身并不解决红-红冲突。它的唯一目的是通过一次旋转，将树的局部结构从"三角"关系（z.p.p -> z.p -> z 形成一个拐角）转化为"线性"关系（z.p.p -> z -> p 形成一条直线）。这样做的结果是，我们现在面对的是 情况 3。

情况 3: `z` 的叔叔是黑色，且 `z` 是一个左孩子 (形成线性关系)

将 z 的父节点 z.p 涂成黑色。

将 z 的祖父节点 z.p.p 涂成红色。

对祖父节点 z.p.p 执行一次右旋操作。

这是 终止情况。这次颜色变换和旋转彻底解决了红-红冲突。让我们分析为什么：

z.p 变成了黑色，所以 z 和 z.p 不再是红-红关系。
旋转后，新的子树根节点 z.p 是黑色的，所以它与它的父节点（原 z.p.p 的父节点）之间不会有红-红冲突。
我们还将原 z.p.p 涂成了红色，原 z.p 涂成了黑色。这看起来改变了颜色，但由于旋转，这个新的子树的黑高保持不变。所有通过这个子树的路径，之前会经过黑色的 z.p.p，现在会经过黑色的 z.p，黑高没有变化。

由于红-红冲突被完全解决，while 循环的条件 (z.p.color == RED) 将不再满足，修复过程结束。

对称情况

我们上面讨论的所有情况都假设 z.p 是 z.p.p 的左孩子。如果 z.p 是 z.p.p 的右孩子，存在三个完全对称的情况：

对称情况 1: 叔叔是红色。（处理方式完全相同）
对称情况 2: 叔叔是黑色，z 是左孩子。（通过右旋转化为对称情况 3）
对称情况 3: 叔叔是黑色，z 是右孩子。（通过左旋终止）

循环的终止和最后一步

while 循环在以下两种情况下终止：

进入情况 3（或其对称情况），问题被彻底解决。
在情况 1 中，问题被不断上推，直到 z 成为根节点。此时 z.p 为 nil，循环条件不满足。

循环结束后，我们必须执行最后一步：T.root.color = BLACK。这确保了性质 2 (根节点是黑色) 始终成立。即使在情况 1 中我们将根节点涂成了红色，这一步也会将其修正回来。这一步不会破坏其他任何性质，因为将根节点从红变黑，只会增加所有路径的黑高，并且增加量是相同的（都是 1），所以性质 5 依然保持。

插入操作的伪代码

RB-INSERT(T, z)
   y = T.nil
   x = T.root
   while x != T.nil
       y = x
       if z.key < x.key
           x = x.left
       else
           x = x.right
   z.p = y
   if y == T.nil
       T.root = z
   else if z.key < y.key
       y.left = z
   else
       y.right = z
   z.left = T.nil
   z.right = T.nil
   z.color = RED
   RB-INSERT-FIXUP(T, z)
 
RB-INSERT-FIXUP(T, z)
    while z.p.color == RED
        if z.p == z.p.p.left
            y = z.p.p.right  // y 是叔叔
            if y.color == RED      // 情况 1
                z.p.color = BLACK
                y.color = BLACK
                z.p.p.color = RED
                z = z.p.p
            else
                if z == z.p.right  // 情况 2
                    z = z.p
                    LEFT-ROTATE(T, z)
                // 情况 3
                z.p.color = BLACK
                z.p.p.color = RED
                RIGHT-ROTATE(T, T.z.p.p)
        else // 对称情况
            y = z.p.p.left   // y 是叔叔
            if y.color == RED      // 对称情况 1
                z.p.color = BLACK
                y.color = BLACK
                z.p.p.color = RED
                z = z.p.p
            else
                if z == z.p.left   // 对称情况 2
                    z = z.p
                    RIGHT-ROTATE(T, z)
                // 对称情况 3
                z.p.color = BLACK
                z.p.p.color = RED
                LEFT-ROTATE(T, z.p.p)
    T.root.color = BLACK

RB-INSERT 中，寻找插入位置的 while 循环耗时 $O(h)$ ，其中 $h$ 是树的高度。
RB-INSERT-FIXUP 中，while 循环在每次迭代中，要么通过情况 1 将 z 指针向上移动两层，要么通过情况 2 和 3 终止循环。因此，循环最多执行 $O(h)$ 次。
循环体内的操作，无论是重新着色还是旋转，都只需要 $O(1)$ 的时间。
因为红黑树的高度 $h$ 保证为 $O(\log n)$ ，所以整个插入操作的总时间复杂度是 $O(\log n)$ 。

这证明了红黑树在插入操作上的高效性，它能够在对数时间内完成插入并保持树的平衡，提供了可预测的、稳定的性能。

删除操作

如果说红黑树的插入操作是精巧的，那么它的删除操作可以说是错综复杂。删除一个节点比插入要困难得多，因为它需要处理更多可能破坏红黑性质的情况。尽管如此，通过一套同样优雅的规则，红黑树的删除操作依然能保证在 $O(\log n)$ 时间内完成，并恢复树的平衡。

与 RB-INSERT 类似，RB-DELETE 也建立在普通二叉搜索树的删除操作之上。我们将使用一个辅助过程 RB-TRANSPLANT，它用一棵子树替换另一棵子树，这与我们在基础 BST 章节中看到的移植操作非常相似。

确定哪个节点 y 是实际要从树中"移除"的节点。

如果待删除节点 z 最多只有一个孩子，那么 y就是 z 本身。
如果 z 有两个孩子，那么 y 就是 z 的后继（successor），即 z 右子树中的最小节点。在这种情况下，y 的内容（key, data）会被复制到 z 中，然后我们转而删除 y。重要的是，y 最多只有一个（右）孩子。

令 x 为 y 的唯一孩子（如果存在）或 T.nil（如果 y 没有孩子）。x 是将要移动到 y 位置的节点。

执行"移植"操作：用 x 替换 y 在树中的位置。

记录 y 的原始颜色。 这是最关键的一步。

如果 y 的原始颜色是黑色，那么树的红黑性质可能被破坏了。我们必须调用 RB-DELETE-FIXUP(T, x) 来修复。

为什么删除黑色节点会引发问题？ 当我们从树中移除一个黑色节点 y 时，所有曾经包含 y 的路径上的黑色节点数量都会减少 1，这就导致这些路径的黑高与不包含 y 的路径不一致，从而违反了黑高性质。此外，如果 y 是黑色的，而它的父节点 p 和替代者 x 都是红色的，那么在 x 替换 y 之后，p 和 x 会形成红-红冲突。更进一步，如果 y 是根节点，而它的一个红色孩子 x 成为了新的根，那么根节点将是红色的，这也违反了红黑树的性质。

相比之下，如果移除的节点 y 是红色的，红黑性质则不会被破坏。因为黑高不变，没有黑色节点被移除；也不会产生红-红冲突，因为 y 的父节点必须是黑色的；红色节点不可能是根节点，除非它是唯一的节点。因此，修复的焦点完全在于被移除的节点 y 是黑色的情况。

`RB-DELETE-FIXUP`: 恢复平衡

当被移除的物理节点 y 是黑色时，我们启动 RB-DELETE-FIXUP(T, x) 程序。x 是顶替了 y 位置的节点。为了弥补丢失的黑色节点，我们给 x 附加一重"额外"的黑色。现在 x 的颜色可以被理解为"红与黑"（如果 x 原本是红色）或"双重黑"（如果 x 原本是黑色）。

如果 x 是“红与黑”，问题很简单：我们直接把它涂成普通的黑色即可。总的黑色数量没有变化，黑高得以恢复。
如果 x 是“双重黑”，它违反了性质 1（节点要么红要么黑）。我们的任务就是通过一个 while 循环，将这重额外的黑色在树中上移或消解掉，直到：
1. x 指向一个"红与黑"节点，此时可将其涂黑并终止。
2. x 指向根节点，此时可以简单地移除这重额外黑色。
3. 通过旋转和重新着色，彻底解决问题。

while 循环的条件是：x 不是根节点，且 x 的颜色是双重黑（在实现中，我们通过一个标志或直接检查其颜色属性来追踪）。在每次迭代中，我们关注 x 和它的兄弟节点 w。

我们假设 x 是其父节点的 左孩子。对称的情况（x 是右孩子）我们稍后讨论。

情况 1: `x` 的兄弟节点 `w` 是红色的

将 w 的颜色设为黑色。

将父节点 p 的颜色设为红色。

对 p 执行一次左旋。

更新 w 为 x 的新兄弟节点。

这个操作的目的是改变局部环境，将情况 1 转化为后续更容易处理的情况。注意，x 的双重黑性质没有改变，但它的兄弟节点现在一定是黑色的了（原 w 的孩子 c）。这次变换保持了黑高性质，并将问题转化为了 x 的兄弟是黑色的情况之一（情况 2, 3, 或 4）。

情况 2: `x` 的兄弟 `w` 是黑色，且 `w` 的两个孩子都是黑色

将 w 的颜色设为红色。

将父节点 p 的颜色设为红色。

这是将问题向上传递的情况。我们将 x 的一重黑色和 w 的黑色（现在 w 变红了）合并，并将其转移到父节点 p 上。也就是说，父节点 p 现在吸收了这重额外的黑色。如果 p 原本是红色，它现在变成黑色（红与黑 -> 黑），问题解决，循环终止。如果 p 原本是黑色，它现在变成了双重黑，循环将在新的 x（即 p）上继续。

情况 3: `x` 的兄弟 `w` 是黑色，`w` 的左孩子是红色，右孩子是黑色 (三角关系)

将 w 的左孩子 c 设为黑色。

将 w 设为红色。

对 w 执行一次右旋。

更新 w 为 x 的新兄弟节点（现在是 c）。

与插入操作中的情况 2 类似，此操作的唯一目的是进行结构转换。它通过旋转和重着色，将“三角”构型转变为“线性”构型，从而将问题转化为最终可解的 情况 4。

情况 4: `x` 的兄弟 `w` 是黑色，且 `w` 的右孩子是红色 (线性关系)

将 w 的颜色设置为 p 的颜色。

将 p 的颜色设置为黑色。

将 w 的右孩子 d 的颜色设置为黑色。

对 p 执行一次左旋。

将 x 指向树的根节点，以终止循环。

这是 终止情况。通过这一系列操作，x 上的额外黑色被彻底消解。w 继承了 p 的颜色，p 变为黑色，d 也变为黑色。旋转之后，新的子树根 w 确保了黑高平衡。x 不再是双重黑，而是普通的黑色。通过将 x 指向根节点，我们确保循环在下一次检查时终止。

删除操作的伪代码

RB-TRANSPLANT(T, u, v)
    if u.p == T.nil
        T.root = v
    else if u == u.p.left
        u.p.left = v
    else
        u.p.right = v
    v.p = u.p
 
RB-DELETE(T, z)
  y = z
  y_original_color = y.color
  if z.left == T.nil
      x = z.right
      RB-TRANSPLANT(T, z, z.right)
  else if z.right == T.nil
      x = z.left
      RB-TRANSPLANT(T, z, z.left)
  else
      y = TREE-MINIMUM(z.right)
      y_original_color = y.color
      x = y.right
      if y.p == z
          x.p = y
      else
          RB-TRANSPLANT(T, y, y.right)
          y.right = z.right
          y.right.p = y
      RB-TRANSPLANT(T, z, y)
      y.left = z.left
      y.left.p = y
      y.color = z.color
  if y_original_color == BLACK
      RB-DELETE-FIXUP(T, x)
 
RB-DELETE-FIXUP(T, x)
  while x != T.root and x.color == BLACK
      if x == x.p.left
          w = x.p.right  // w 是兄弟
          if w.color == RED      // 情况 1
              w.color = BLACK
              x.p.color = RED
              LEFT-ROTATE(T, x.p)
              w = x.p.right
          if w.left.color == BLACK and w.right.color == BLACK // 情况 2
              w.color = RED
              x = x.p
          else
              if w.right.color == BLACK // 情况 3
                  w.left.color = BLACK
                  w.color = RED
                  RIGHT-ROTATE(T, w)
                  w = x.p.right
              // 情况 4
              w.color = x.p.color
              x.p.color = BLACK
              w.right.color = BLACK
              LEFT-ROTATE(T, x.p)
              x = T.root
      else // 对称情况 (x 是右孩子)
          // ... (与上面逻辑对称)
  x.color = BLACK

复杂度分析

RB-DELETE 中，确定要删除的节点 y 和执行移植操作需要 $O(h)$ 时间。
RB-DELETE-FIXUP 中，while 循环的行为决定了复杂度。
- 情况 1, 3, 4 通过常数次旋转和重着色来解决问题或转化问题，然后循环会终止。
- 情况 2 将 x 指针向上移动一层。
- 因此，循环最多执行 $O(h)$ 次。
循环体内的所有操作都是 $O(1)$ 的。
由于红黑树的高度 $h$ 保证为 $O(\log n)$ ，所以整个删除操作的总时间复杂度是 $O(\log n)$ 。

尽管删除操作的逻辑比插入要复杂得多，但它仍然维持了红黑树高效的对数时间性能保证，这正是其在高性能系统中被广泛应用的核心原因。

性能回顾

经过对红黑树内部机制的深入剖析，我们现在可以退后一步，宏观地审视这种数据结构的卓越之处。红黑树作为自平衡二叉搜索树的杰出代表，其设计哲学集中体现了在保证最坏情况性能与维持较低操作成本之间的精妙权衡。

红黑树的核心思想在于它是一种特殊的二叉搜索树，通过引入颜色属性和五条性质约束来维持树的平衡。红黑树的本质是遵循二叉搜索树的基本性质，确保元素的有序性，从而使查找操作高效。五大性质中，尤其是红色节点无红孩子和统一黑高这两条，确保了从根到叶子的最长路径不会超过最短路径的两倍，将树的高度限制在 $O(\log n)$ 。红黑树通过动态平衡维护来保持其性质，每次插入和删除操作后，都会通过重新着色和旋转这两种基本工具进行修复。重新着色用于满足红黑属性，旋转则是调整父子关系以恢复平衡。最终，这些机制为所有基本动态集操作提供了稳定的 $O(\log n)$ 的最坏情况时间复杂度，避免了普通二叉搜索树在有序数据下性能退化的问题。

为了更直观地理解红黑树的优势，下表比较了它与其他几种常见数据结构在基本操作上的性能：

数据结构	查找 (平均)	查找 (最坏)	插入 (平均)	插入 (最坏)	删除 (平均)	删除 (最坏)
无序数组	$O(n)$	$O(n)$	$O(1)$	$O(1)$	$O(n)$	$O(n)$
有序数组	$O(\log n)$	$O(\log n)$	$O(n)$	$O(n)$	$O(n)$	$O(n)$
链表	$O(n)$	$O(n)$	$O(1)$	$O(1)$	$O(n)$	$O(n)$
二叉搜索树	$O(\log n)$	$O(n)$	$O(\log n)$	$O(n)$	$O(\log n)$	$O(n)$
红黑树	$O(\log n)$	$O(\log n)$	$O(\log n)$	$O(\log n)$	$O(\log n)$	$O(\log n)$

从表中可以清晰地看到，红黑树是唯一一种在所有核心操作的最坏情况下都能维持对数时间性能的动态数据结构。这使得它成为构建数据库索引、内存管理器、调度器以及各种标准库（如 C++ std::map, Java TreeMap）的理想选择。

AVL 树

值得一提的是，红黑树并非唯一的自平衡二叉搜索树。另一种著名的实现是 AVL 树，它比红黑树的平衡条件更严格。AVL 树要求任何节点的左右子树高度差不能超过 1。这种严格的平衡性使得 AVL 树的查找性能通常略快于红黑树。

然而，天下没有免费的午餐。更严格的平衡意味着在插入和删除时，需要进行更频繁、可能更复杂的旋转操作来维护平衡。因此，对于写操作（插入、删除）密集型的应用，红黑树通常表现更好，因为它允许“适度”的不平衡，从而减少了维护开销。红黑树的这种实用主义哲学，使其在现实世界的应用中获得了更广泛的青睐。

红黑树

红黑树的性质

节点颜色性质 (Color Property): 每个节点要么是红色的，要么是黑色的。
根节点性质 (Root Property): 根节点是黑色的。
叶子节点性质 (Leaf Property): 每个叶子节点（NIL）是黑色的。
红色节点性质 (Red Property): 如果一个节点是红色的，则它的两个子节点都必须是黑色的。
黑色高度性质 (Black-Height Property): 对每个节点，从该节点到其所有后代叶子节点（NIL）的简单路径上，均包含相同数目的黑色节点。

根据性质 4，任何路径上红色节点不能相邻，所以黑色节点至少占一半。
根据性质 5，每条路径的黑色节点数量相等（我们称之为树的黑高 $bh$ ）。
考虑最短的路径：这条路径完全由黑色节点组成，其长度就是树的黑高 $bh$ 。
考虑最长的路径：由于红色节点不能相邻，这条路径最多是黑红交替的，即 B-R-B-R...。因此，其长度最多是 $2 \times bh$ 。

旋转操作

旋转分为两种基本类型：左旋（Left-Rotate） 和 右旋（Right-Rotate）。这两种操作是互为逆运算的。

左旋 (Left-Rotate)

确定 y: 令 $y$ 为 $x$ 的右子节点。如前所述， $y$ 必须存在。

更新 y 的父指针: $y$ 将取代 $x$ 在树中的位置。我们将 $x$ 的父节点 $p$ 赋给 $y$ 的父节点，即 y.p = x.p。

如果 $x$ 原本是根节点（x.p == T.nil），那么 $y$ 现在就成为新的根节点 (T.root = y)。
如果 $x$ 是其父节点的左孩子，那么 $y$ 就成为 $x$ 父节点的新的左孩子 (x.p.left = y)。
如果 $x$ 是其父节点的右孩子，那么 $y$ 就成为 $x$ 父节点的新的右孩子 (x.p.right = y)。

连接 x 和 y: 最后，我们将 $x$ 设置为 $y$ 的左孩子，y.left = x，并更新 $x$ 的父指针指向 $y$ ，x.p = y。

在上图中，我们可以看到左旋操作的核心变化：

节点 x（红色节点）从父节点的直接子节点变成了 y 的左子节点
节点 y（绿色节点）从 x 的右子节点变成了父节点的直接子节点
子树 β（y 的左子树）从 y 的左子树变成了 x 的右子树
子树 α 和 γ 的位置保持不变，只是它们的父节点关系发生了变化

伪代码实现：

LEFT-ROTATE(T, x)
    y = x.right                 # 步骤 1: 确定 y
    x.right = y.left            # 步骤 2: 将 y 的左子树 β 设为 x 的右子树
    if y.left != T.nil
        y.left.p = x
    y.p = x.p                     # 步骤 3: y 继承 x 的父节点
    if x.p == T.nil
        T.root = y
    else if x == x.p.left
        x.p.left = y
    else
        x.p.right = y
    y.left = x                    # 步骤 4: 将 x 设为 y 的左孩子
    x.p = y

右旋 (Right-Rotate)

伪代码实现：

RIGHT-ROTATE(T, y)
    x = y.left                  # 步骤 1: 确定 x
    y.left = x.right            # 步骤 2: 将 x 的右子树 β 设为 y 的左子树
    if x.right != T.nil
        x.right.p = y
    x.p = y.p                     # 步骤 3: x 继承 y 的父节点
    if y.p == T.nil
        T.root = x
    else if y == y.p.left
        y.p.left = x
    else
        y.p.right = x
    x.right = y                   # 步骤 4: 将 y 设为 x 的右孩子
    y.p = x

旋转操作的时间复杂度

插入操作

标准的二叉搜索树插入： 首先，我们忽略颜色，像在普通的二叉搜索树中一样，为新节点找到合适的位置并将其插入。

修复红黑性质： 插入新节点后，某些红黑性质可能会被破坏。我们需要一个修复程序，通过一系列的重新着色和旋转操作，来恢复这些性质。

RB-INSERT(T, z) 算法的概要：

使用一个指针 y (作为尾随指针) 和 x (作为遍历指针) 从根节点开始，按照二叉搜索树的规则向下查找，为新节点 z 找到一个合适的父节点 y。

将 z 作为 y 的孩子插入。

将新插入的节点 z 的左右孩子设为 T.nil。

将新节点 z 的颜色设置为红色。

调用一个辅助程序 RB-INSERT-FIXUP(T, z) 来解决可能由此引发的红黑性质冲突。

为什么将新节点涂成红色？。让我们分析一下，插入一个红色的新节点 z 会破坏哪些性质：

性质 1 (颜色): 满足，因为节点是红色或黑色。
性质 2 (根节点): 如果 z 是根节点，那么根是红色的，违反了此性质。但这很容易修复，只需在最后将根节点涂黑即可。
性质 3 (叶子): 满足，z 的叶子是黑色的 NIL 节点。
性质 4 (红色节点): 这是最可能被破坏的性质。如果 z 的父节点 p 也是红色的，那么我们就有了两个连续的红色节点，这被称为"红-红冲突"。
性质 5 (黑色高度): 这个性质一定会被满足！ 因为新插入的红色节点 z 不会改变任何路径上的黑色节点数量。所有路径的黑高都保持不变。

`RB-INSERT-FIXUP`: 修复红-红冲突

情况 1: `z` 的叔叔节点是红色的

条件: z 的父节点 z.p 是红色的，且 z 的叔叔节点 y 也是红色的。

将 z 的父节点 z.p 涂成黑色。

将 z 的叔叔节点 y 涂成黑色。

将 z 的祖父节点 z.p.p 涂成红色。

将指针 z 移动到其祖父节点 z.p.p 上，即 z = z.p.p。

情况 2: `z` 的叔叔是黑色，且 `z` 是一个右孩子 (形成三角关系)

将指针 z 移动到其父节点 z.p 上，即 z = z.p。

对新的 z (也就是旧的 z.p) 执行一次左旋操作。

情况 3: `z` 的叔叔是黑色，且 `z` 是一个左孩子 (形成线性关系)

将 z 的父节点 z.p 涂成黑色。

将 z 的祖父节点 z.p.p 涂成红色。

对祖父节点 z.p.p 执行一次右旋操作。

这是 终止情况。这次颜色变换和旋转彻底解决了红-红冲突。让我们分析为什么：

z.p 变成了黑色，所以 z 和 z.p 不再是红-红关系。
旋转后，新的子树根节点 z.p 是黑色的，所以它与它的父节点（原 z.p.p 的父节点）之间不会有红-红冲突。
我们还将原 z.p.p 涂成了红色，原 z.p 涂成了黑色。这看起来改变了颜色，但由于旋转，这个新的子树的黑高保持不变。所有通过这个子树的路径，之前会经过黑色的 z.p.p，现在会经过黑色的 z.p，黑高没有变化。

由于红-红冲突被完全解决，while 循环的条件 (z.p.color == RED) 将不再满足，修复过程结束。

对称情况

我们上面讨论的所有情况都假设 z.p 是 z.p.p 的左孩子。如果 z.p 是 z.p.p 的右孩子，存在三个完全对称的情况：

对称情况 1: 叔叔是红色。（处理方式完全相同）
对称情况 2: 叔叔是黑色，z 是左孩子。（通过右旋转化为对称情况 3）
对称情况 3: 叔叔是黑色，z 是右孩子。（通过左旋终止）

循环的终止和最后一步

while 循环在以下两种情况下终止：

进入情况 3（或其对称情况），问题被彻底解决。
在情况 1 中，问题被不断上推，直到 z 成为根节点。此时 z.p 为 nil，循环条件不满足。

插入操作的伪代码

RB-INSERT(T, z)
   y = T.nil
   x = T.root
   while x != T.nil
       y = x
       if z.key < x.key
           x = x.left
       else
           x = x.right
   z.p = y
   if y == T.nil
       T.root = z
   else if z.key < y.key
       y.left = z
   else
       y.right = z
   z.left = T.nil
   z.right = T.nil
   z.color = RED
   RB-INSERT-FIXUP(T, z)
 
RB-INSERT-FIXUP(T, z)
    while z.p.color == RED
        if z.p == z.p.p.left
            y = z.p.p.right  // y 是叔叔
            if y.color == RED      // 情况 1
                z.p.color = BLACK
                y.color = BLACK
                z.p.p.color = RED
                z = z.p.p
            else
                if z == z.p.right  // 情况 2
                    z = z.p
                    LEFT-ROTATE(T, z)
                // 情况 3
                z.p.color = BLACK
                z.p.p.color = RED
                RIGHT-ROTATE(T, T.z.p.p)
        else // 对称情况
            y = z.p.p.left   // y 是叔叔
            if y.color == RED      // 对称情况 1
                z.p.color = BLACK
                y.color = BLACK
                z.p.p.color = RED
                z = z.p.p
            else
                if z == z.p.left   // 对称情况 2
                    z = z.p
                    RIGHT-ROTATE(T, z)
                // 对称情况 3
                z.p.color = BLACK
                z.p.p.color = RED
                LEFT-ROTATE(T, z.p.p)
    T.root.color = BLACK

RB-INSERT 中，寻找插入位置的 while 循环耗时 $O(h)$ ，其中 $h$ 是树的高度。
RB-INSERT-FIXUP 中，while 循环在每次迭代中，要么通过情况 1 将 z 指针向上移动两层，要么通过情况 2 和 3 终止循环。因此，循环最多执行 $O(h)$ 次。
循环体内的操作，无论是重新着色还是旋转，都只需要 $O(1)$ 的时间。
因为红黑树的高度 $h$ 保证为 $O(\log n)$ ，所以整个插入操作的总时间复杂度是 $O(\log n)$ 。

这证明了红黑树在插入操作上的高效性，它能够在对数时间内完成插入并保持树的平衡，提供了可预测的、稳定的性能。

删除操作

确定哪个节点 y 是实际要从树中"移除"的节点。

如果待删除节点 z 最多只有一个孩子，那么 y就是 z 本身。
如果 z 有两个孩子，那么 y 就是 z 的后继（successor），即 z 右子树中的最小节点。在这种情况下，y 的内容（key, data）会被复制到 z 中，然后我们转而删除 y。重要的是，y 最多只有一个（右）孩子。

令 x 为 y 的唯一孩子（如果存在）或 T.nil（如果 y 没有孩子）。x 是将要移动到 y 位置的节点。

执行"移植"操作：用 x 替换 y 在树中的位置。

记录 y 的原始颜色。 这是最关键的一步。

如果 y 的原始颜色是黑色，那么树的红黑性质可能被破坏了。我们必须调用 RB-DELETE-FIXUP(T, x) 来修复。

`RB-DELETE-FIXUP`: 恢复平衡

如果 x 是“红与黑”，问题很简单：我们直接把它涂成普通的黑色即可。总的黑色数量没有变化，黑高得以恢复。
如果 x 是“双重黑”，它违反了性质 1（节点要么红要么黑）。我们的任务就是通过一个 while 循环，将这重额外的黑色在树中上移或消解掉，直到：
1. x 指向一个"红与黑"节点，此时可将其涂黑并终止。
2. x 指向根节点，此时可以简单地移除这重额外黑色。
3. 通过旋转和重新着色，彻底解决问题。

我们假设 x 是其父节点的 左孩子。对称的情况（x 是右孩子）我们稍后讨论。

情况 1: `x` 的兄弟节点 `w` 是红色的

将 w 的颜色设为黑色。

将父节点 p 的颜色设为红色。

对 p 执行一次左旋。

更新 w 为 x 的新兄弟节点。

情况 2: `x` 的兄弟 `w` 是黑色，且 `w` 的两个孩子都是黑色

将 w 的颜色设为红色。

将父节点 p 的颜色设为红色。

情况 3: `x` 的兄弟 `w` 是黑色，`w` 的左孩子是红色，右孩子是黑色 (三角关系)

将 w 的左孩子 c 设为黑色。

将 w 设为红色。

对 w 执行一次右旋。

更新 w 为 x 的新兄弟节点（现在是 c）。

情况 4: `x` 的兄弟 `w` 是黑色，且 `w` 的右孩子是红色 (线性关系)

将 w 的颜色设置为 p 的颜色。

将 p 的颜色设置为黑色。

将 w 的右孩子 d 的颜色设置为黑色。

对 p 执行一次左旋。

将 x 指向树的根节点，以终止循环。

删除操作的伪代码

RB-TRANSPLANT(T, u, v)
    if u.p == T.nil
        T.root = v
    else if u == u.p.left
        u.p.left = v
    else
        u.p.right = v
    v.p = u.p
 
RB-DELETE(T, z)
  y = z
  y_original_color = y.color
  if z.left == T.nil
      x = z.right
      RB-TRANSPLANT(T, z, z.right)
  else if z.right == T.nil
      x = z.left
      RB-TRANSPLANT(T, z, z.left)
  else
      y = TREE-MINIMUM(z.right)
      y_original_color = y.color
      x = y.right
      if y.p == z
          x.p = y
      else
          RB-TRANSPLANT(T, y, y.right)
          y.right = z.right
          y.right.p = y
      RB-TRANSPLANT(T, z, y)
      y.left = z.left
      y.left.p = y
      y.color = z.color
  if y_original_color == BLACK
      RB-DELETE-FIXUP(T, x)
 
RB-DELETE-FIXUP(T, x)
  while x != T.root and x.color == BLACK
      if x == x.p.left
          w = x.p.right  // w 是兄弟
          if w.color == RED      // 情况 1
              w.color = BLACK
              x.p.color = RED
              LEFT-ROTATE(T, x.p)
              w = x.p.right
          if w.left.color == BLACK and w.right.color == BLACK // 情况 2
              w.color = RED
              x = x.p
          else
              if w.right.color == BLACK // 情况 3
                  w.left.color = BLACK
                  w.color = RED
                  RIGHT-ROTATE(T, w)
                  w = x.p.right
              // 情况 4
              w.color = x.p.color
              x.p.color = BLACK
              w.right.color = BLACK
              LEFT-ROTATE(T, x.p)
              x = T.root
      else // 对称情况 (x 是右孩子)
          // ... (与上面逻辑对称)
  x.color = BLACK

复杂度分析

RB-DELETE 中，确定要删除的节点 y 和执行移植操作需要 $O(h)$ 时间。
RB-DELETE-FIXUP 中，while 循环的行为决定了复杂度。
- 情况 1, 3, 4 通过常数次旋转和重着色来解决问题或转化问题，然后循环会终止。
- 情况 2 将 x 指针向上移动一层。
- 因此，循环最多执行 $O(h)$ 次。
循环体内的所有操作都是 $O(1)$ 的。
由于红黑树的高度 $h$ 保证为 $O(\log n)$ ，所以整个删除操作的总时间复杂度是 $O(\log n)$ 。

尽管删除操作的逻辑比插入要复杂得多，但它仍然维持了红黑树高效的对数时间性能保证，这正是其在高性能系统中被广泛应用的核心原因。

性能回顾

为了更直观地理解红黑树的优势，下表比较了它与其他几种常见数据结构在基本操作上的性能：

数据结构	查找 (平均)	查找 (最坏)	插入 (平均)	插入 (最坏)	删除 (平均)	删除 (最坏)
无序数组	$O(n)$	$O(n)$	$O(1)$	$O(1)$	$O(n)$	$O(n)$
有序数组	$O(\log n)$	$O(\log n)$	$O(n)$	$O(n)$	$O(n)$	$O(n)$
链表	$O(n)$	$O(n)$	$O(1)$	$O(1)$	$O(n)$	$O(n)$
二叉搜索树	$O(\log n)$	$O(n)$	$O(\log n)$	$O(n)$	$O(\log n)$	$O(n)$
红黑树	$O(\log n)$	$O(\log n)$	$O(\log n)$	$O(\log n)$	$O(\log n)$	$O(\log n)$

红黑树

红黑树的性质

旋转操作

左旋 (Left-Rotate)

右旋 (Right-Rotate)

旋转操作的时间复杂度

插入操作

RB-INSERT-FIXUP: 修复红-红冲突

情况 1: z 的叔叔节点是红色的

情况 2: z 的叔叔是黑色，且 z 是一个右孩子 (形成三角关系)

情况 3: z 的叔叔是黑色，且 z 是一个左孩子 (形成线性关系)

对称情况

循环的终止和最后一步

插入操作的伪代码

删除操作

RB-DELETE-FIXUP: 恢复平衡

情况 1: x 的兄弟节点 w 是红色的

情况 2: x 的兄弟 w 是黑色，且 w 的两个孩子都是黑色

情况 3: x 的兄弟 w 是黑色，w 的左孩子是红色，右孩子是黑色 (三角关系)

情况 4: x 的兄弟 w 是黑色，且 w 的右孩子是红色 (线性关系)

删除操作的伪代码

复杂度分析

性能回顾

AVL 树

红黑树

红黑树的性质

旋转操作

左旋 (Left-Rotate)

右旋 (Right-Rotate)

旋转操作的时间复杂度

插入操作

RB-INSERT-FIXUP: 修复红-红冲突

情况 1: z 的叔叔节点是红色的

情况 2: z 的叔叔是黑色，且 z 是一个右孩子 (形成三角关系)

情况 3: z 的叔叔是黑色，且 z 是一个左孩子 (形成线性关系)

对称情况

循环的终止和最后一步

插入操作的伪代码

删除操作

RB-DELETE-FIXUP: 恢复平衡

情况 1: x 的兄弟节点 w 是红色的

情况 2: x 的兄弟 w 是黑色，且 w 的两个孩子都是黑色

情况 3: x 的兄弟 w 是黑色，w 的左孩子是红色，右孩子是黑色 (三角关系)

情况 4: x 的兄弟 w 是黑色，且 w 的右孩子是红色 (线性关系)

删除操作的伪代码

复杂度分析

性能回顾

AVL 树

`RB-INSERT-FIXUP`: 修复红-红冲突

情况 1: `z` 的叔叔节点是红色的

情况 2: `z` 的叔叔是黑色，且 `z` 是一个右孩子 (形成三角关系)

情况 3: `z` 的叔叔是黑色，且 `z` 是一个左孩子 (形成线性关系)

`RB-DELETE-FIXUP`: 恢复平衡

情况 1: `x` 的兄弟节点 `w` 是红色的

情况 2: `x` 的兄弟 `w` 是黑色，且 `w` 的两个孩子都是黑色

情况 3: `x` 的兄弟 `w` 是黑色，`w` 的左孩子是红色，右孩子是黑色 (三角关系)

情况 4: `x` 的兄弟 `w` 是黑色，且 `w` 的右孩子是红色 (线性关系)

`RB-INSERT-FIXUP`: 修复红-红冲突

情况 1: `z` 的叔叔节点是红色的

情况 2: `z` 的叔叔是黑色，且 `z` 是一个右孩子 (形成三角关系)

情况 3: `z` 的叔叔是黑色，且 `z` 是一个左孩子 (形成线性关系)

`RB-DELETE-FIXUP`: 恢复平衡

情况 1: `x` 的兄弟节点 `w` 是红色的

情况 2: `x` 的兄弟 `w` 是黑色，且 `w` 的两个孩子都是黑色

情况 3: `x` 的兄弟 `w` 是黑色，`w` 的左孩子是红色，右孩子是黑色 (三角关系)

情况 4: `x` 的兄弟 `w` 是黑色，且 `w` 的右孩子是红色 (线性关系)