数据结构

数据结构是算法的基石，就像建筑需要钢筋水泥一样，优秀的算法离不开高效的数据结构支撑。本部分我们将探讨最核心的数据结构，当然学过我们数据结构内容的可以跳过这个部分。

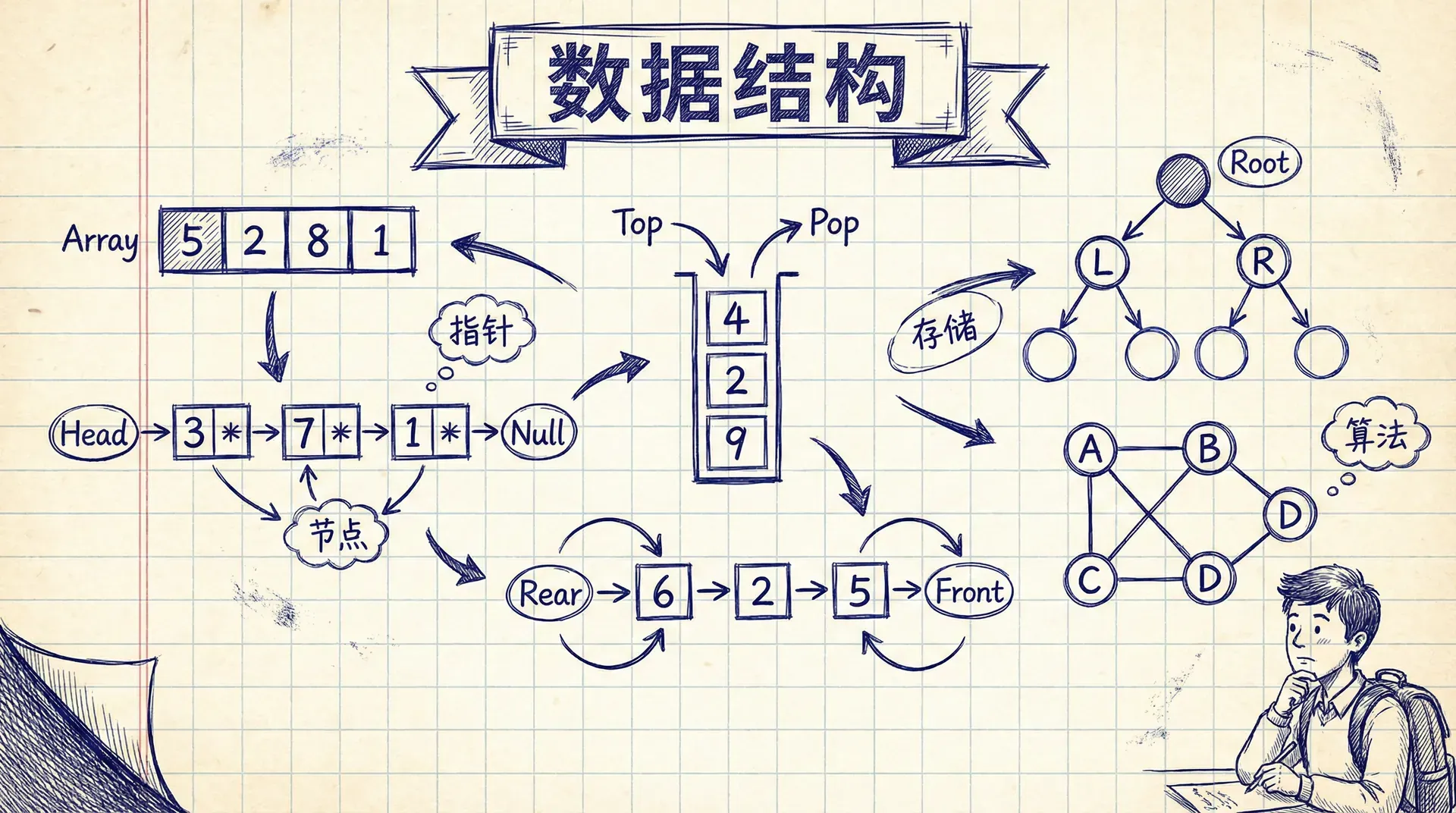
栈与队列

栈和队列是两种最基本的动态集合，它们的特殊之处在于删除操作是预先规定的——你无法选择删除哪个元素，只能按照特定的规则进行。

栈：后进先出（LIFO）

栈是一种遵循“后进先出”（LIFO）原则的线性数据结构。可以将其想象成一摞盘子或一个子弹夹，最后放入的元素总是第一个被取出。 这种特性使得栈在某些应用场景中非常有用，例如在函数调用中，最新的调用需要最先返回。栈的操作主要包括压入（PUSH）、弹出（POP）和查看栈顶元素（TOP），这些操作都遵循LIFO原则。

核心操作：

• PUSH(S, x): 将元素 x 压入栈顶
• POP(S): 弹出栈顶元素
• TOP(S): 查看栈顶元素（不删除）
• IS_EMPTY(S): 检查栈是否为空

|
class Stack:
    def __init__(self):
        self.items = []
        self.top = -1  # 栈顶指针
    
    def push(self, x):
        self.top += 1
        self.items.append(x)
    
    def pop(self):
        if self.is_empty():
            raise Exception("Stack underflow")
        self.top -= 1
        return self.items.pop()
    
    def peek(self):
        if self.is_empty():
            return None
        return self.items[self.top]
    
    def is_empty(self):
        return self.top == -1

• 所有操作的时间复杂度：$O(1)$
• 空间复杂度：$O(n)$

栈在计算机科学中有着广泛的应用。它用于管理函数调用的顺序，确保最新的调用最先返回。此外，栈在括号匹配检查中用于追踪未闭合的括号，确保表达式的正确性。 在图的深度优先搜索（DFS）中，栈用于记录访问路径，帮助算法回溯。栈还在表达式求值中用于处理操作数和运算符的优先级，确保计算的正确性。

队列

队列操作遵循“先进先出”（FIFO）的原则。这意味着在队列中，最先进入队列的元素会最先被处理， 就像在售票窗口排队一样，最早到达的人会最先买到票。队列的这种特性使其非常适合用于需要按顺序处理任务的场景。

核心操作：

• ENQUEUE(Q, x): 将元素 x 加入队尾
• DEQUEUE(Q): 从队头取出元素
• FRONT(Q): 查看队头元素
• IS_EMPTY(Q): 检查队列是否为空

|
class Queue:
    def __init__(self, capacity=10):
        self.items = [None] * capacity
        self.head = 0  # 队头指针
        self.tail = 0  # 队尾指针
        self.size = 0
        self.capacity = capacity
    
    def enqueue(self, x):
        if

• 基本操作：$O(1)$ 均摊时间
• 空间复杂度：$O(n)$

队列是一种非常重要的数据结构，广泛应用于多种计算机科学和工程领域：

1. 广度优先搜索（BFS）：在图论中，队列用于实现广度优先搜索算法。BFS是一种遍历或搜索图的算法，通常用于寻找最短路径或在无权图中查找所有节点。
2. 任务调度：在操作系统中，队列用于管理任务的调度。任务按照到达的顺序排队等待处理，确保公平和高效的资源分配。
3. 消息传递：在分布式系统中，队列用于消息传递机制。消息队列可以在不同的系统或进程之间传递信息，确保消息的有序传递和可靠性。
4. 缓冲管理：在计算机网络和多媒体应用中，队列用于缓冲管理。数据包或多媒体流在传输过程中被暂时存储在队列中，以应对网络延迟或带宽波动。

栈与队列的比较

链表

数组是一种线性数据结构，允许通过索引快速访问元素，这使得查找操作非常高效。 然而，数组在插入和删除元素时效率较低，因为这些操作可能需要移动大量元素。 此外，数组的大小在初始化时是固定的，无法动态调整。相比之下，链表是一种更灵活的数据结构。 链表由一系列节点组成，每个节点包含数据和指向下一个节点的指针。 通过这种方式，链表可以轻松地进行插入和删除操作，因为只需调整指针即可，不需要移动其他元素。 链表的大小也可以根据需要动态增长或缩小。

单向链表

单向链表是链表中最简单的形式。在这种结构中，每个节点都包含一个数据部分和一个指向下一个节点的指针。 由于每个节点只指向下一个节点，因此链表的遍历只能从头节点开始，逐个访问到链表的末尾。 这种结构使得在链表头部插入新节点非常高效，但在链表中间或尾部插入和删除节点时，可能需要遍历多个节点。

|
class Node:
    def __init__(self, key):
        self.key = key
        self.next = None
 
class SinglyLinkedList:
    def __init__(self):
        self.head = None
    
    def insert_front(self, key):
        """在链表头部插入新节点"""
        new_node = Node(key)
        new_node.next = self.head
        self

双向链表

在双向链表中，每个节点都包含两个指针：一个指向前一个节点（prev），另一个指向后一个节点（next）。 这种结构使得我们可以从任意节点开始，轻松地向前或向后遍历整个链表。 此外，双向链表的这种双向指针特性使得删除操作更加高效，因为我们可以直接访问要删除节点的前驱节点， 从而在常数时间内更新指针，避免了单向链表中需要从头遍历以找到前驱节点的情况。

|
class DoublyNode:
    def __init__(self, key):
        self.key = key
        self.prev = None
        self.next = None
 
class DoublyLinkedList:
    def __init__(self):
        self.head = None
        self.tail = None
    
    def insert_front(self, key):
        """在链表头部插入"""

• 搜索：$O(n)$
• 插入（已知位置）：$O(1)$
• 删除（已知位置）：$O(1)$
• 空间复杂度：$O(n)$

链表可视化

哈希表

哈希表是一种高效的数据结构，通过使用哈希函数将键映射到数组中的特定索引位置。 这个过程使得哈希表能够在平均情况下以常数时间复杂度 $O(1)$ 进行查找、插入和删除操作。 哈希表的核心在于哈希函数，它负责将输入的键转换为数组的索引，从而快速定位存储的数据。 由于哈希表的这种特性，它在需要快速数据访问的场景中非常有用。

哈希函数设计

一个理想的哈希函数需要具备以下特性：首先，它应当能够将键值均匀地分布在整个数组中，以避免聚集。 其次，计算过程应当简便，以确保高效的性能。最后，它应当尽量减少不同键值映射到相同位置的概率，从而降低冲突的发生。

|
def hash_function(key, size):
    """简单的哈希函数示例"""
    return hash(key) % size
 
def hash_string(s, size):
    """字符串哈希函数"""
    hash_val = 0
    for char in s:
        hash_val = (hash_val * 31 + ord(char)) % size
    return hash_val

冲突解决策略

链地址法（Separate Chaining）

链地址法（Separate Chaining）是一种用于解决哈希表中冲突的策略。 当多个键被映射到同一个索引时，链地址法通过在该索引处维护一个链表来存储所有冲突的键值对。 这种方法的优点是简单易实现，并且在负载因子较低时性能较好。 然而，当链表变长时，查找和删除操作的性能可能会下降，因此需要合理设计哈希函数以减少冲突的发生。

|
class HashTable:
    def __init__(self, size=100):
        self.size = size
        self.table = [[] for _ in range(size)]
    
    def insert(self, key, value):
        index = hash_function(key, self.size)
        # 检查是否已存在
        for item in self.table[index]:
            if item[

开放寻址法（Open Addressing）

开放寻址法（Open Addressing）是一种解决哈希表冲突的策略。与链地址法不同，开放寻址法在哈希表内部寻找空闲位置来存储冲突的键值对。 常见的开放寻址策略包括线性探测、二次探测和双重哈希。开放寻址法的优点是避免了链表的额外空间开销，但在负载因子较高时，性能可能会下降。

在开放寻址法中，删除操作需要特别注意，因为直接删除可能会导致查找失败。 因此，通常使用一个标记数组来标识被删除的位置，以便后续的查找操作能够继续进行。 开放寻址法适用于需要高效利用内存的场景，但需要合理设计哈希函数和探测策略以减少冲突和探测次数。

|
class HashTableOpenAddressing:
    def __init__(self, size=100):
        self.size = size
        self.table = [None] * size
        self.deleted = [False] * size
    
    def insert(self, key, value):
        for i in range(self.size):

• 平均情况：$O(1)$ 查找、插入、删除
• 最坏情况：$O(n)$（所有元素哈希到同一位置）
• 空间复杂度：$O(n)$

在数据库系统中，哈希表常用于实现索引，以加速数据的检索过程。在缓存系统中，哈希表用于快速存取缓存数据，从而提高系统的响应速度。 此外，哈希表是字典或映射数据结构的基础，实现键值对的高效存储和查找。同时在去重算法中，哈希表通过快速检测重复元素，帮助实现数据的唯一性检查。

树

树是一种非线性的层次结构数据结构。在树中，每个节点可以有多个子节点，但只有一个父节点，根节点是 唯一没有父节点的节点。树的这种层次结构使其非常适合表示具有层级关系的数据。例如，在文件系统中，目 录和文件可以用树来表示，其中目录是节点，文件是叶子节点。在组织结构中，树可以用来表示员工的层级关系，根节点可能是CEO，其他节点是各级管理人员和员工。 此外，表达式树用于表示数学表达式，其中每个节点是一个操作符或操作数，子节点是操作数或子表达式。

二叉树

在二叉树这种数据结构中，每个节点最多可以拥有两个子节点，分别称为左子节点和右子节点。 这种结构使得二叉树在许多应用中非常有用，例如在搜索算法中，二叉搜索树可以通过其有序的结构快速查找元素。 此外，二叉树还可以用于表达式解析、堆排序等场景。二叉树的层次结构使其适合表示具有分支特性的关系。

|
class TreeNode:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None
        self.parent = None
 
class BinaryTree:
    def __init__(self):
        self.root = None
    
    def insert(self, key):
        """插入新节点"""

树的遍历方式：

|
def preorder_traversal(node):
    """前序遍历：根-左-右"""
    if node:
        print(node.key, end=" ")
        preorder_traversal(node.left)
        preorder_traversal(node.right)
 
def inorder_traversal(node):
    """中序遍历：左-根-右"""
    if node:
        inorder_traversal(node.left)
        print(node.key, end=" ")
        inorder_traversal(node.right)
 
def postorder_traversal(node):
    """后序遍历：左-右-根"""
    if node:

堆：特殊的完全二叉树

堆是一种特殊的完全二叉树，具有以下特性：

1. 完全二叉树结构：堆总是保持完全二叉树的形态，这意味着每一层都被完全填满，除了最后一层，节点从左到右依次填充。

2. 堆性质：

   • 最大堆：在最大堆中，每个父节点的值都大于或等于其子节点的值。这意味着根节点包含整个堆中的最大值。
   • 最小堆：在最小堆中，每个父节点的值都小于或等于其子节点的值。这意味着根节点包含整个堆中的最小值。

这种结构和性质使得堆在实现优先队列等数据结构时非常高效，能够在对数时间内完成插入和删除操作。

|
class MaxHeap:
    def __init__(self):
        self.heap = []
    
    def parent(self, i):
        return (i - 1) // 2
    
    def left_child(self, i):
        return 2 * i + 1
    
    def right_child(self, i):
        return 2 * i 

• 插入：$O(\log n)$
• 删除最大值：$O(\log n)$
• 获取最大值：$O(1)$
• 建堆：$O(n)$

堆在计算机科学中有着广泛的应用。它被用于实现优先队列，支持高效的插入和删除最大值操作。 此外，我们之前学过的堆排序是一种基于堆的数据排序算法，能够在 $O(n \log n)$ 时间内对数据进行排序。 在图算法中，堆被用于优化Dijkstra和Prim算法的性能，帮助快速找到最短路径或最小生成树。 堆还在任务调度中用于管理任务的优先级，确保高效的资源分配。

左孩子-右兄弟表示法

在计算机科学中，“左孩子-右兄弟”表示法是一种将多叉树（即每个节点可以有多个子节点的树）转换为二叉树（即每个节点最多有两个子节点的树）的方法。 具体来说，对于每个节点，我们将其第一个子节点作为左孩子，其他子节点依次作为右兄弟连接。 这样，原本的多叉树结构就可以通过二叉树来表示。这种表示法在实现和操作复杂树结构时非常有用，因为二叉树的操作通常比多叉树更简单和高效。

|
class TreeNode:
    def __init__(self, key):
        self.key = key
        self.left_child = None    # 第一个子节点
        self.right_sibling = None # 右兄弟节点
 
class Tree:
    def __init__(self):
        self.root = None
    
    def add_child(self, parent, key):
        """为父节点添加子节点"""
        new_node =

这里我们简单探讨了栈、队列、链表、哈希表和树等基础数据结构，它们各自适用于不同场景，如LIFO、FIFO、快速查找和层次化结构，理解这些特性和复杂度是设计高效算法的基础。

以下是一些常见场景的推荐：

在实际应用中，我们常常需要在时间和空间之间做出权衡。例如，哈希表提供快速查找但需要额外空间，而链表节省空间但查找较慢。选择时需要考虑具体的使用场景和性能要求。