线性时间排序

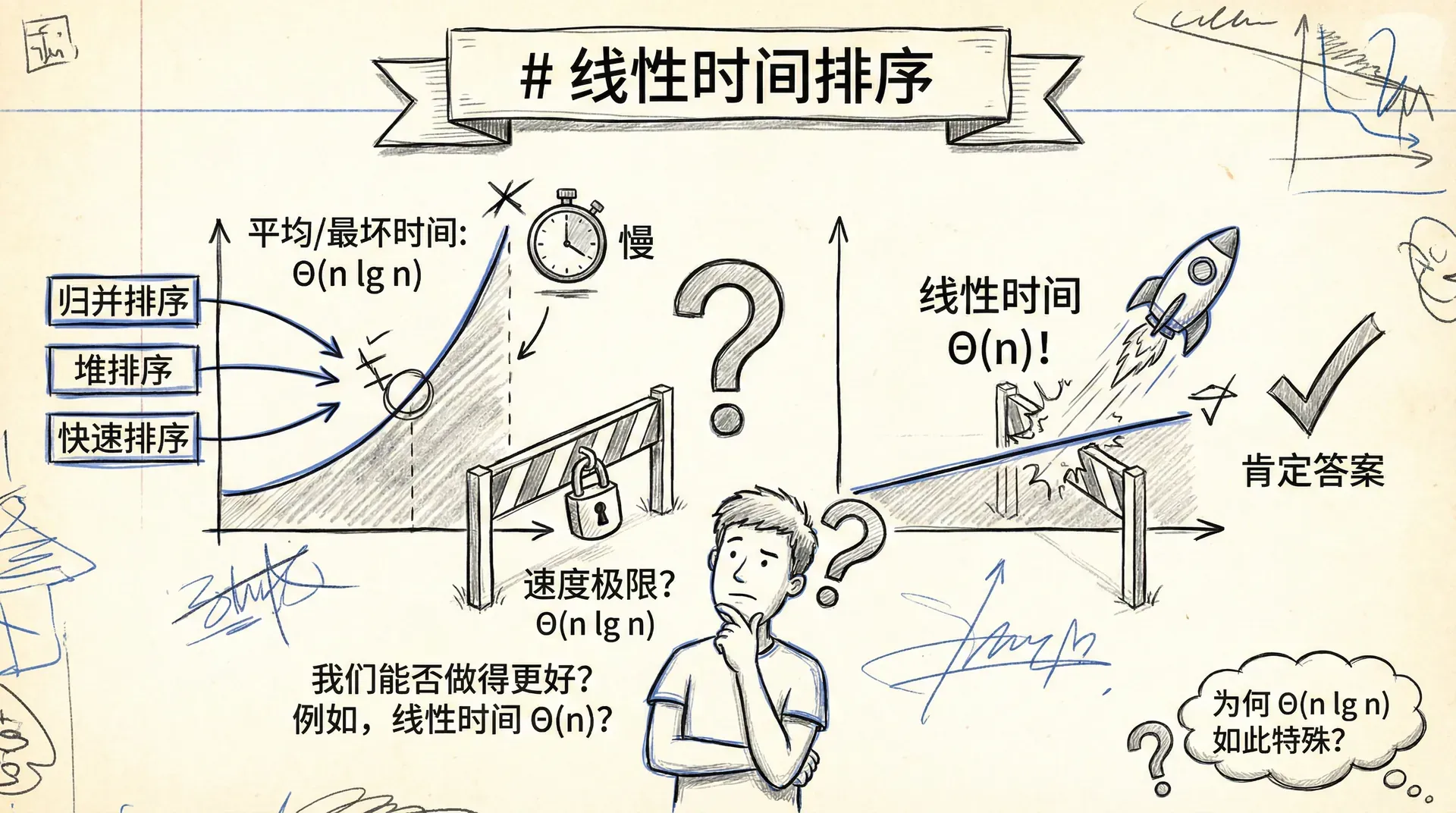
到目前为止，我们所学习的归并排序、堆排序和快速排序等算法，其最快的运行时间（无论是平均还是最坏情况）都达到了 $\Theta(n \lg n)$。 这引出了一个深刻的问题：排序算法的速度极限就是 $\Theta(n \lg n)$ 吗？我们能否做得更好，例如，在线性时间 $\Theta(n)$ 内完成排序？ 这里我们将给出肯定的答案。但在此之前，我们首先需要理解为何 $\Theta(n \lg n)$ 如此特殊。

比较排序的下界

我们目前接触的所有排序算法，都有一个共同点：它们通过比较元素之间的大小来确定最终的顺序。我们称这类算法为比较排序（Comparison Sort）。 为了理解比较排序的极限，我们可以引入一个抽象的模型——决策树（Decision Tree）。一棵决策树能够表示一个比较排序算法在处理一个特定规模（例如 $n=3$）的输入时，所做的全部比较序列。

• 树的每个内部节点代表一次 a[i] 与 a[j] 的比较。
• 节点的两个分支分别对应比较结果的两种可能。
• 树的每个叶子节点代表一种可能的排序结果，即输入元素的一种排列。

对于一个包含 $n$ 个元素的输入，总共有 $n!$ 种可能的排列。一个正确的排序算法必须能够区分并产出这 $n!$ 种排列中的任何一种。因此，它的决策树必须至少有 $n!$ 个叶子节点。

在一棵高度为 $h$ 的二叉树中，叶子节点的数量最多为 $2^h$。所以，我们有： $n! \le 2^h$

两边取对数，得到： $h \ge \lg(n!)$

根据近似公式，我们知道 $\lg(n!) = \Theta(n \lg n)$。

因此，任何基于比较的排序算法，在最坏情况下，都需要进行至少 $\Omega(n \lg n)$ 次比较。

这个定理为比较排序算法的速度设定了一个无法逾越的理论下界。归并排序和堆排序达到了这个下界，因此它们是渐进最优的比较排序算法。 那么，如何才能打破这个“音障”，实现线性时间排序呢？答案是：不使用比较。 接下来的几种算法，通过对输入数据做出一些特殊的假设，绕过了比较的限制，从而实现了惊人的线性时间效率。

计数排序

计数排序（Counting Sort）是一种简单而高效的非比较排序算法。它的核心思想是：如果我知道有多少个元素比我小，那我不就知道我的位置了吗？ 计数排序要求输入数据是在某个确定范围内的整数。例如，对一个由 0 到 k 之间整数组成的数组进行排序。

假设输入数组 $A = \langle 2, 5, 3, 0, 2, 3, 0, 3 \rangle$，其中 $k=5$。

最终得到 B = <0, 0, 2, 2, 3, 3, 3, 5>。

时间复杂度：如果输入范围是 $k$，输入规模是 $n$，则时间复杂度为 $\Theta(n+k)$。当 $k = O(n)$ 时，计数排序就是线性时间的。

基数排序

如果需要排序的整数范围很大（例如 32 位整数），计数排序就不适用了，因为它需要一个巨大的计数数组。基数排序（Radix Sort）巧妙地解决了这个问题。 基数排序模拟了老式卡片分拣机的工作方式。它不是一次性比较整个数字，而是逐位地进行排序，从最低位（最不重要位）开始，一直到最高位。

假设我们现在对数字 $\langle 329, 457, 657, 839, 436, 720, 355 \rangle$ 排序:

时间复杂度：如果数字有 $d$ 位，每一位有 $k$ 种可能（例如十进制是 10，二进制是 2），并且使用计数排序作为子程序，则总时间复杂度为 $\Theta(d(n+k))$。 通过巧妙地选择基数（例如，将 32 位整数看作 4 个 8 位数），基数排序通常可以在线性时间内完成。

桶排序

桶排序（Bucket Sort）是一种高效的线性时间排序算法，特别适用于特定类型的数据集。 它的高效性依赖于一个重要的假设，即输入数据是独立且均匀地分布在一个已知的范围内。通常，这个范围被设定为 [0, 1)，这意味着所有待排序的元素都是在 0 和 1 之间的实数。 桶排序通过将数据分配到多个桶中，并在每个桶内进行排序来实现整体排序。由于数据的均匀分布，每个桶内的元素数量相对较少，从而使得桶内排序的过程非常快速。

由于数据是均匀分布的，我们期望每个桶里的元素数量会很少。如果每个桶里只有常数个元素，那么对每个桶的排序就会非常快。

假设输入数组 $A = \langle 0.78, 0.17, 0.39, 0.26, 0.72, 0.94, 0.21, 0.12, 0.23, 0.68 \rangle$，其中 $n=10$。

在输入数据满足均匀分布的假设下，桶排序的平均时间复杂度是 $\Theta(n)$。尽管它的最坏情况时间复杂度是 $\Theta(n^2)$（例如所有元素都掉进同一个桶里），但在实践中，对于符合其假设的数据，它的性能非常出色。

小练习

1. 比较排序下界

   • 为什么任何基于比较的排序算法在最坏情况下都需要至少 $\Omega(n \lg n)$ 次比较？
   • 决策树的高度与排序算法性能有什么关系？

2. 计数排序

   • 计数排序为什么要求输入数据在确定范围内？
   • 为什么计数排序是稳定的？稳定性有什么重要性？

3. 基数排序

   • 为什么基数排序必须使用稳定的排序算法作为子程序？
   • 如果从高位到低位排序，会发生什么问题？

4. 桶排序

   • 桶排序为什么要求数据均匀分布？
   • 如果所有元素都掉进同一个桶里，时间复杂度会变成什么？

5. 计数排序实现

   |
   # 请实现计数排序算法
   def counting_sort(A, k):
       # 你的代码 here
       pass

6. 基数排序实现

   |
   # 请实现基数排序算法（假设输入是正整数）
   def radix_sort(A):
       # 你的代码 here
   

桶内排序：对每个非空桶内的元素进行排序（使用插入排序）：

• 桶1: [0.12, 0.17]
• 桶2: [0.21, 0.23, 0.26]
• 桶3: [0.39]
• 桶6: [0.68]
• 桶7: [0.72, 0.78]
• 桶9: [0.94]