3 / 11

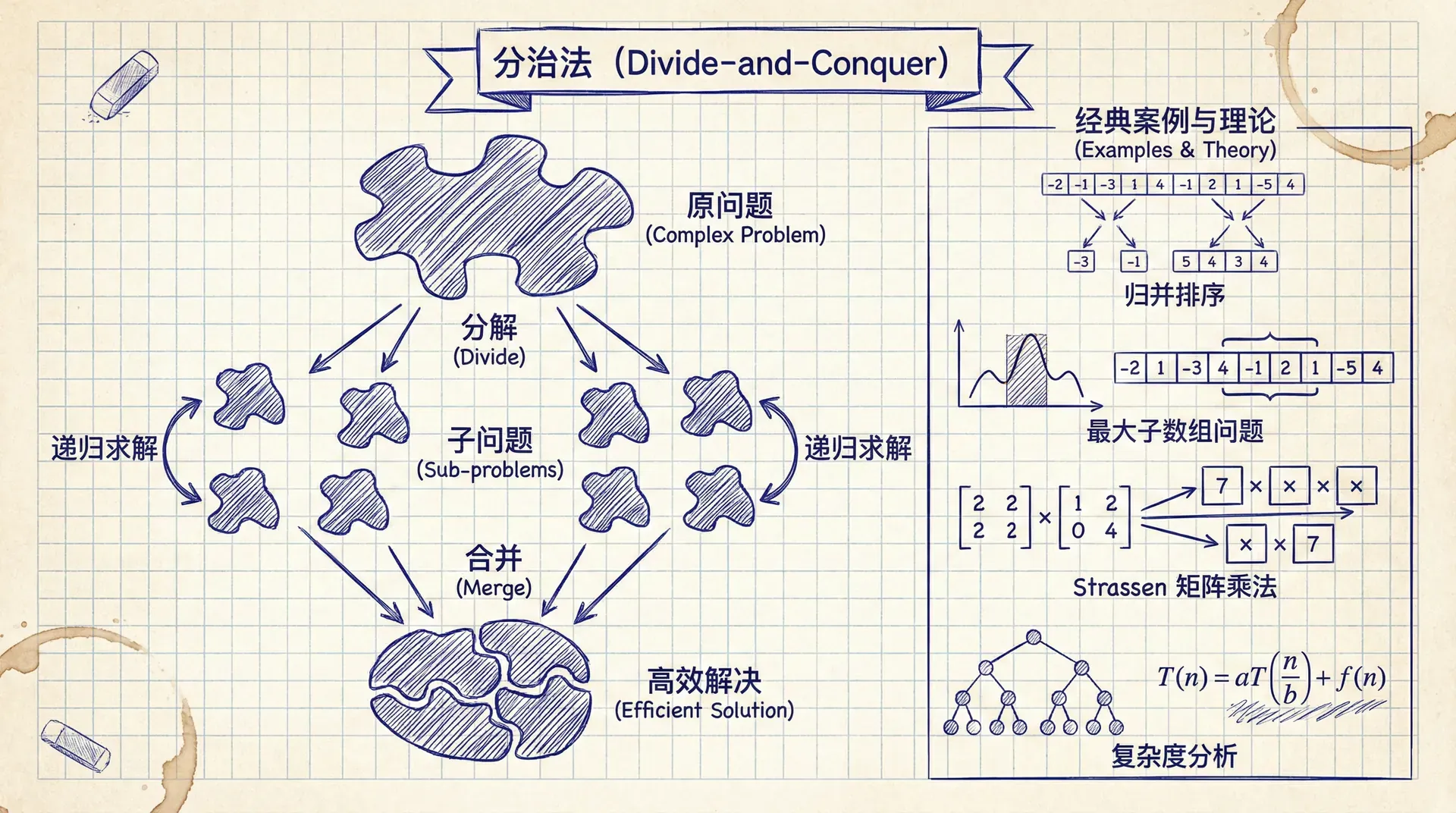
分治法

分治法（Divide-and-Conquer）是算法设计中的核心范式之一，通过将复杂问题分解为结构相似的子问题，递归求解后合并结果，从而高效地解决原问题。在算法入门部分，我们已通过归并排序初步了解了分治法的基本思想。本章将系统阐述分治法的理论框架，并通过最大子数组问题和 Strassen 矩阵乘法两个经典案例，深入探讨分治法在算法设计中的应用及其复杂度分析。

分治法

分治法的核心思想

分治法采用递归策略，其执行过程可形式化为三个基本阶段：

分解（Divide）：将原问题 $P$ 分解为 $k$ 个规模更小的子问题 $P_1, P_2, \ldots, P_k$ ，其中每个子问题 $P_i$ 的结构与原问题 $P$ 相同，但规模更小。

解决（Conquer）：递归地求解各子问题。若子问题规模足够小，可直接求解（称为基本情况，Base Case）；否则继续递归分解（称为递归情形，Recursive Case）。

合并（Combine）：将各子问题的解 $S_1, S_2, \ldots, S_k$ 合并，构造原问题的解。

分治法并非适用于所有问题。一个问题能够有效应用分治法，需满足以下必要条件：

可分解性：问题可分解为规模更小的同类型子问题，且子问题规模严格小于原问题规模
子问题独立性：子问题之间相互独立，求解一个子问题不影响其他子问题的求解过程
合并可行性：子问题的解可在多项式时间内合并为原问题的解
规模递减性：子问题规模必须严格递减，确保递归过程在有限步内终止

分治法的优势与局限

优势	局限
将复杂问题转化为简单子问题，降低求解难度	递归调用产生的函数调用栈开销可能抵消分治带来的性能收益
天然支持并行化处理，子问题可独立并行求解	合并步骤可能成为算法性能瓶颈，影响整体效率
算法结构清晰，易于理解、实现和维护	对于某些问题，分治法的时间复杂度可能不如其他算法设计方法

最大子数组问题

最大子数组问题（Maximum Subarray Problem）是算法设计中的经典问题。给定一个包含 $n$ 个元素的数组 $A[1..n]$ ，其中每个元素 $A[i]$ 表示第 $i$ 个元素的值，目标是找到数组 $A$ 中元素和最大的连续子数组，并返回该子数组的起始位置、结束位置及其元素和。

形式化地，我们需要找到索引 $i$ 和 $j$ （ $1 \leq i \leq j \leq n$ ），使得 $\sum_{k=i}^{j} A[k]$ 达到最大值。

例如，对于数组 $A = [13, -3, -25, 20, -3, -16, -23, 18, 20, -7, 12, -5, -22, 15, -4, 7]$ ，最大子数组为，其元素和为。

暴力求解方法需要检查所有可能的子数组，共有 $\binom{n+1}{2} = \frac{n(n+1)}{2}$ 个子数组，时间复杂度为。采用分治法可将时间复杂度降低至。

分治求解策略

对于数组 $A[\text{low}..\text{high}]$ ，设其中点索引为 $\text{mid} = \lfloor(\text{low} + \text{high})/2\rfloor$ 。最大子数组的位置存在三种可能情形：

完全位于左子数组 $A[\text{low}..\text{mid}]$ 中
完全位于右子数组 $A[\text{mid}+1..\text{high}]$ 中
跨越中点 $\text{mid}$ ，即包含 $A[\text{mid}]$ 和 $A [$

前两种情形可通过递归求解。第三种情形"跨越中点"是合并步骤的关键。跨越中点的最大子数组必然由两部分组成：左半部分 $A[i..\text{mid}]$ 和右半部分 $A[\text{mid}+1..j]$ ，其中 $i \in [\text{low}, \text{mid}]$ ， $j \in [mid +$ 。

我们可在 $\Theta(\text{high} - \text{low})$ 时间内找到这样的索引对 $(i, j)$ ，方法是从 $\text{mid}$ 开始分别向左、向右扫描，寻找和最大的子数组。

以下是寻找跨越中点的最大子数组的算法：

|
FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high)
1  left-sum = -∞                    // 初始化左半部分最大和
2  sum = 0                          // 当前累加和
3  for i = mid downto low          // 从mid向左扫描
4      sum = sum + A[i]             // 累加当前元素
5      if sum > left-

基于上述辅助函数，可构造完整的分治算法：

|
FIND-MAXIMUM-SUBARRAY(A, low, high)
1  if high == low                   // 基本情况：只有一个元素
2      return (low, high, A[low])   // 返回该元素本身
3  else
4      mid = floor((low + high) / 2)  // 计算中点
5      (left-low, left-high, left-sum) = FIND-

时间复杂度分析：设 $T(n)$ 表示算法处理长度为 $n$ 的数组的运行时间。算法将问题分解为两个规模为 $n/2$ 的子问题，合并步骤（寻找跨越中点的最大子数组）需要 $\Theta(n)$ 时间。因此，递推关系为：

$T(n) = 2T(n/2) + \Theta(n)$

根据主方法（Master Method），该递推式的解为 $T(n) = \Theta(n \lg n)$ ，优于暴力解法的 $\Theta(n^2)$ 。

线性时间解法：Kadane 算法

尽管分治法将最大子数组问题的时间复杂度从 $\Theta(n^2)$ 降低至 $\Theta(n \lg n)$ ，但存在更优的线性时间算法——Kadane 算法。

Kadane 算法的核心思想基于动态规划：维护两个变量，max_ending_here 表示以当前位置结尾的最大子数组和，max_so_far 表示迄今为止找到的最大子数组和。算法的关键洞察是：若以位置 $i-1$ 结尾的最大子数组和为负，则将其丢弃，从位置 $i$ 重新开始计算，因为负的子数组和不可能对后续结果产生正贡献。

|
KADANE-MAXIMUM-SUBARRAY(A)
1  max-so-far = A[1]                // 全局最大和，初始化为第一个元素
2  max-ending-here = A[1]            // 以当前位置结尾的最大和
3  start = 1                         // 最大子数组起始位置
4  end = 1                           // 最大子数组结束位置
5

复杂度分析：Kadane 算法的时间复杂度为 $\Theta(n)$ ，空间复杂度为 $\Theta(1)$ ，是解决最大子数组问题的最优算法。

Strassen 矩阵乘法

矩阵乘法是线性代数中的基本运算，在科学计算、机器学习、图像处理等领域有广泛应用。给定两个 $n \times n$ 矩阵 $A$ 和 $B$ ，其乘积 $C = A \cdot B$ 是一个 $n \times n$ 矩阵，其中元素定义为：

$c_{ij} = \sum_{k=1}^{n} a_{ik} b_{kj}$

标准矩阵乘法算法需要计算 $n^2$ 个元素，每个元素需要 $n$ 次乘法和 $n-1$ 次加法，因此时间复杂度为 $\Theta(n^3)$ 。

朴素的分治解法

采用分治法，将 $n \times n$ 矩阵分解为 4 个 $(n/2) \times (n/2)$ 的子矩阵。设：

C = \begin{pmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{pmatrix}, \quad A = \begin{pmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{pmatrix}, \quad B = \begin{pmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{pmatrix}

则矩阵乘法可表示为：

\begin{pmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{pmatrix} = \begin{pmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{pmatrix} \begin{pmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{pmatrix}

展开后得到：

\begin{align} C_{11} &= A_{11}B_{11} + A_{12}B_{21} \\ C_{12} &= A_{11}B_{12} + A_{12}B_{22} \\ C_{21} &= A_{21}B_{11} + A_{22}B_{21} \\ C_{22} &= A_{21}B_{12} + A_{22}B_{22} \end{align}

该分治策略需要 8 次 $(n/2) \times (n/2)$ 规模的矩阵乘法和 4 次矩阵加法。矩阵加法的时间复杂度为 $\Theta(n^2)$ ，因此递推关系为：

$T(n) = 8T(n/2) + \Theta(n^2)$

根据主方法， $a = 8$ ， $b = 2$ ， $f(n) = \Theta(n^2)$ 。计算 $\log_{b} a = \log_{2}$ ，因此。由于（其中），属于主方法的情况一，因此。这表明朴素的分治策略并未带来性能提升。

Strassen 算法

1969 年，Volker Strassen 提出了一种突破性的矩阵乘法算法，通过巧妙的代数变换，将子问题的矩阵乘法次数从 8 次减少至 7 次，代价是增加了加法和减法运算次数（共 18 次）。其递推关系为：

$T(n) = 7T(n/2) + \Theta(n^2)$

复杂度分析：根据主方法， $a = 7$ ， $b = 2$ ， $f(n) = \Theta(n^2)$ 。计算 $\log_{b} a = \log_{}$ ，因此。由于（其中），属于主方法的情况一，因此：

$T(n) = \Theta(n^{\log_2 7}) = \Theta(n^{2.81})$

与标准算法的 $\Theta(n^3)$ 相比，Strassen 算法在理论上实现了更优的时间复杂度。对于大规模矩阵运算，这种改进尤为显著。

Strassen 算法的执行步骤：

分解阶段：将矩阵 $A$ 、 $B$ 、 $C$ 分别分解为 4 个 $(n/2) \times (n/2)$ 的子矩阵、、、和、、、。

求解递推式的方法

分治算法的时间复杂度通常由形如 $T(n) = aT(n/b) + f(n)$ 的递推关系描述，其中 $a \geq 1$ ， $b > 1$ ，为渐近非负函数。本节系统介绍求解此类递推关系的三种主要方法。

代入法

代入法（Substitution Method）是一种严格的证明技术，通过数学归纳法验证对递推式解的猜测。其基本步骤为：

猜测解的形式：基于递归树、经验或类似问题的解，猜测 $T(n)$ 的渐近界
验证猜测：使用数学归纳法证明猜测的正确性，通常需要确定合适的常数

示例：证明 $T(n) = 2T(n/2) + n$ 的解为 $T(n) = O(n \lg n)$

猜测：存在常数 $c > 0$ ，使得 $T(n) \leq cn \lg n$ 对所有足够大的 $n$ 成立。

归纳证明：假设对于所有 $m < n$ ， $T(m) \leq cm \lg m$ 成立。则：

\begin{aligned} T (n) & = 2 T (n / 2) + n \\ \leq 2 \cdot c (n / 2) \lg (n / 2) + n \\ = c n \lg (n / 2) + n \\ = c n (\lg n - \lg 2) + n \\ = c n \lg n - c n + n \\ = c n \lg n - ( \end{aligned}

为使 $T(n) \leq cn \lg n$ 成立，需要 $(c-1)n \geq 0$ ，即 $c \geq 1$ 。选择，并验证基本情况，即可完成证明。

在应用代入法时，必须严格导出所假设的不等式形式。有时需要强化归纳假设，即从猜测中减去一个低阶项（如 $T(n) \leq cn \lg n - dn$ ），以确保归纳步骤能够成立。

递归树法

递归树法（Recursion-Tree Method）通过可视化递推关系来生成解的猜测，特别适用于分析复杂递推式。在递归树中，每个节点表示一个子问题的成本，树的深度对应递归的层数。

示例：分析 $T(n) = 3T(n/4) + cn^2$ 的递归树

分析过程：

树的高度：递归在 $n/4^i = 1$ 时终止，即 $i = \log_4 n$ ，因此树的高度为 $\log_4 n$

$T(n) = \sum_{i=0}^{\log_4 n} cn^2\left(\frac{3}{16}\right)^i = cn^2 \sum_{i=0}^{\log_4 n} \left(\frac{3}{16}\right)^i$

由于 $3/16 < 1$ ，该几何级数收敛，其和的上界为常数。因此 $T(n) = O(n^2)$ 。进一步分析可证明 $T(n) = \Theta(n^2)$ 。

递归树法的一般步骤：

构造递归树，标注每个节点的成本

计算树的高度（递归深度）

计算每一层的总成本

对所有层的成本求和，得到总成本的表达式

主方法

主方法（Master Method）提供了求解形如 $T(n) = aT(n/b) + f(n)$ 的递推关系的系统化方法，其中 $a \geq 1$ ， $b > 1$ ，为渐近非负函数。

主定理：设 $T(n) = aT(n/b) + f(n)$ ，其中 $a \geq 1$ ， $b > 1$ ，为渐近非负函数。定义，则的渐近行为如下：

情况一：若 $f(n) = O(n^{\log_b a - \varepsilon})$ ，其中 $\varepsilon > 0$ ，则。

主方法为分治算法的时间复杂度分析提供了系统化的工具。通过比较 $f(n)$ 与 $n^{\log_b a}$ 的渐近关系，可快速确定算法的复杂度，而无需构造递归树或进行复杂的归纳证明。

应用主方法的步骤

识别参数：确定 $a$ （子问题个数）、 $b$ （问题规模缩小比例）和 $f(n)$ （分解与合并的成本）
计算关键值：计算 $\log_b a$ ，得到 $n^{\log_b a}$

经典应用示例

示例 1：归并排序

递推式： $T(n) = 2T(n/2) + n$
参数： $a = 2$ ， $b = 2$ ， $f(n) = n$

示例 2：二分查找

递推式： $T(n) = T(n/2) + 1$
参数： $a = 1$ ， $b = 2$ ， $f(n) = 1$

示例 3：Strassen 矩阵乘法

递推式： $T(n) = 7T(n/2) + \Theta(n^2)$
参数： $a = 7$ ， $b = 2$ ，

主方法仅适用于特定形式的递推关系。若递推式不符合 $T(n) = aT(n/b) + f(n)$ 的形式，或 $f(n)$ 不满足主定理的条件，则需使用递归树法或代入法等其他方法。

小练习

分治法的适用性分析：判断以下问题是否适合采用分治法求解，并给出理论依据：
- 计算斐波那契数列的第 $n$ 项
- 寻找数组中的最大值
- 判断一个字符串是否为回文串
- 计算两个大整数的乘积
- 寻找数组中的众数（出现次数最多的元素）
分治算法设计：设计一个分治算法寻找数组中的第二大元素。要求：
- 时间复杂度为 $O(n)$
- 空间复杂度为 $O(\lg n)$ （递归栈空间）
最近点对问题：给定平面上 $n$ 个点，找到距离最近的两个点。
- 设计一个基于分治的算法
- 分析算法的时间复杂度
- 实现算法的关键步骤
逆序对计数：给定一个数组 $A[1..n]$ ，计算其中逆序对的数量。逆序对定义为：若且，则是一个逆序对。

mid

+

1

]

A[\text{mid}+1]

1

,

high

]

j \in [\text{mid}+1, \text{high}]

8

=

3

\log_b a = \log_2 8 = 3

2

7

\approx

2.81

\log_b a = \log_2 7 \approx 2.81

c

-

1

)

n

\begin{align} T(n) &= 2T(n/2) + n \\ &\leq 2 \cdot c(n/2) \lg(n/2) + n \\ &= cn \lg(n/2) + n \\ &= cn(\lg n - \lg 2) + n \\ &= cn \lg n - cn + n \\ &= cn \lg n - (c-1)n \end{align}

c = 1

分治 | 自在学

S_{8} & = B_{21} + B_{22}

S_{9} & = A_{11} - A_{21}

S_{10} & = B_{11} + B_{12}

\begin{align} S_1 &= B_{12} - B_{22} \\ S_2 &= A_{11} + A_{12} \\ S_3 &= A_{21} + A_{22} \\ S_4 &= B_{21} - B_{11} \\ S_5 &= A_{11} + A_{22} \\ S_6 &= B_{11} + B_{22} \\ S_7 &= A_{12} - A_{22} \\ S_8 &= B_{21} + B_{22} \\ S_9 &= A_{11} - A_{21} \\ S_{10} &= B_{11} + B_{12} \end{align}

5

\cdot

S_{6}

=

(

A_{11}

+

A_{22}

)

(

B_{11}

+

B_{22}

)

P_{6} & = S_{7} \cdot S_{8} = (A_{12} - A_{22}) (B_{21} + B_{22})

P_{7} & = S_{9} \cdot S_{10} = (A_{11} - A_{21}) (B_{11} + B_{12})

\begin{align} P_1 &= A_{11} \cdot S_1 = A_{11}(B_{12} - B_{22}) \\ P_2 &= S_2 \cdot B_{22} = (A_{11} + A_{12})B_{22} \\ P_3 &= S_3 \cdot B_{11} = (A_{21} + A_{22})B_{11} \\ P_4 &= A_{22} \cdot S_4 = A_{22}(B_{21} - B_{11}) \\ P_5 &= S_5 \cdot S_6 = (A_{11} + A_{22})(B_{11} + B_{22}) \\ P_6 &= S_7 \cdot S_8 = (A_{12} - A_{22})(B_{21} + B_{22}) \\ P_7 &= S_9 \cdot S_{10} = (A_{11} - A_{21})(B_{11} + B_{12}) \end{align}