动态规划
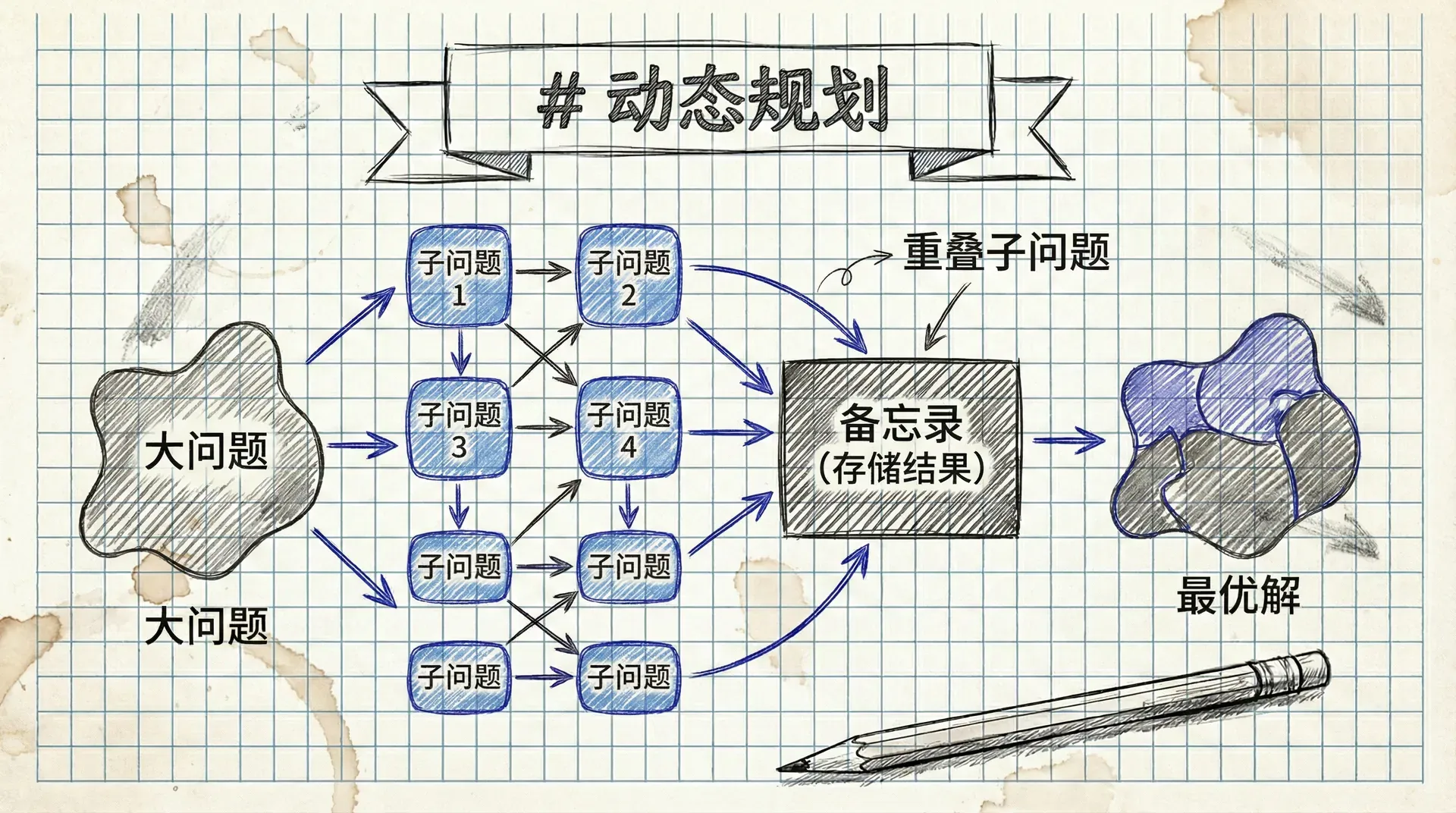
一种解决问题的强大思想
在算法设计的世界里,动态规划(Dynamic Programming, DP)是一种极其强大和重要的思想。它通常用于解决最优化问题(optimization problems), 这类问题要求我们在众多可能的解中,找到那个最优的(最大、最小、最长、最短等)。例如,在地图上找到两个城市之间的最短路径,或者在给定背包容量和一系列物品的情况下,装入价值最高的物品组合。
动态规划与我们之前学习过的“分治法”(Divide and Conquer)有一定的相似之处,因为它们都试图将一个大问题分解为若干个小规模的子问题来求解。然而,它们之间有一个本质的区别:
- 分治法 所处理的子问题通常是相互独立的。例如,在归并排序中,排序左半部分数组和排序右半部分数组是两个完全不相干的任务。
- 动态规划 所处理的子问题往往是相互重叠、相互依赖的。一个子问题的解可能会被其他多个父问题反复使用。
如果用朴素的递归来解决这类问题,我们会发现大量的计算被浪费在反复求解相同的子问题上。动态规划的核心精髓就在于,它能够聪明地“记住”已经解决过的子问题的答案,并在需要时直接取用,从而避免了这种冗余计算。
为了更直观地理解这一点,让我们来看一个经典的例子:计算斐波那契数列。其递归定义如下:
,其中 。
一个简单的递归计算斐波那契数列的实现如下:
|RECURSIVE-FIB(n) if n <= 1 return n else return RECURSIVE-FIB(n - 1) + RECURSIVE-FIB(n - 2)
让我们分析一下计算 RECURSIVE-FIB(6) 时的递归调用树:
观察上图可以发现惊人的浪费:
F_4被计算了 2 次。F_3被计算了 3 次。F_2被计算了 5 次。
... 随着 n 的增大,这种重复计算会呈指数级增长,算法的时间复杂度高达 。
动态规划正是为了解决这类**“重叠子问题”(Overlapping Subproblems)**而生的。它通过存储(缓存)子问题的解,确保每个子问题只被计算一次。一个问题能够用动态规划解决,通常具备两个清晰的标志:
- 最优子结构 (Optimal Substructure): 一个问题的最优解包含其子问题的最优解。这意味着我们可以通过组合子问题的最优解,来构造出整个问题的最优解。
- 重叠子问题 (Overlapping Subproblems): 在问题的求解过程中,许多相同的子问题会被反复计算。
在本部分中,我们将系统学习设计动态规划算法的两种主要方法,并通过一系列经典的案例,深入剖析如何运用动态规划思想来解决复杂的优化问题。
动态规划的实现方法
实现动态规划算法通常有两种途径:带备忘录的自顶向下法,和自底向上的列表法。尽管思路略有不同,但它们都利用了“重叠子问题”的特性,有着相同的渐进时间复杂度。
方法一:带备忘录的自顶向下法 (Top-down with Memoization)
这种方法保留了自然的递归形式,但做了一个简单的增强:备忘(Memoization)。我们可以将其理解为一种“聪明的递归”。 其工作流程如下:
设置一个“备忘录”(memo),通常是一个数组或哈希表,用于存储已经计算出的子问题的解。初始化时,备忘录中填充一个特殊值,表示该问题尚未被求解。
在递归函数中,我们首先检查备忘录。
- 如果当前子问题的解已经存在于备忘录中,直接返回该解,不再进行任何计算。
- 如果不存在,则按照常规的递归方式计算该子问题的解。
在计算出解之后,将其存入备忘录,然后再返回。
让我们用这种方法来改造斐波那契数列的计算(伪代码):
|MEMOIZED-FIB(n) # 1. 初始化一个大小为 n+1 的备忘录数组 memo,填充特殊值(如 -1) let memo[0...n] be a new array for i = 0 to n memo[i] = -1 return LOOKUP-FIB(n, memo) LOOKUP-FIB(n, memo) # 2. 检查备忘录 if memo[n] >= 0 return memo[n] # 3. 如果不在备忘录中,则计算 if n <= 1 result = n else
通过备忘录,LOOKUP-FIB(k) 对于每个 k 只会真正计算一次。所有后续的调用都将直接从备忘录中以 的时间复杂度获取结果。因此,算法的总时间复杂度从 急剧下降到 。
方法二:自底向上的列表法 (Bottom-up Tabulation)
这种方法完全摒弃了递归,采用一种更直接的迭代方式。它通常被称为列表法(Tabulation),因为它需要填充一张表格(通常是一维或二维数组),按顺序计算子问题的解。 其工作流程如下:
确定子问题求解的顺序。对于一个规模为 n 的问题,我们通常需要求解规模为 1, 2, ..., n-1 的所有子问题。
创建一个表格(列表),用于存储从最小到最大的所有子问题的解。
按照预定的顺序,从最小的子问题开始,依次计算并填充表格。计算当前问题的解时,我们会利用表格中已经存好的、更小子问题的解。
再次以斐波那契数列为例:
为了计算 F_n,我们需要 F_{n-1} 和 F_{n-2}。而为了计算 F_{n-1},我们需要 F_{n-2} 和 F_{n-3},以此类推。这揭示了求解的自然顺序:从 F_0, F_1 开始,依次计算 F_2, F_3, ..., 直到 F_n。
伪代码:
|BOTTOM-UP-FIB(n) if n <= 1 return n # 1. 创建一个表格 dp,大小为 n+1 let dp[0...n] be a new array # 2. 初始化最小子问题的解 dp[0] = 0 dp[1] = 1 # 3. 按照顺序,自底向上填充表格 for i = 2 to n dp[i] = dp[i-1] + dp[i-
这种方法同样保证了每个子问题只计算一次,时间复杂度为 。在实践中,由于它避免了递归调用的开销,其运行速度通常比备忘录法要快一些,空间复杂度也可能更优。
两种方法的比较
设计动态规划算法的步骤
虽然动态规划问题千变万化,但解决它们的过程通常遵循一个固定的模式。我们可以将这个模式总结为以下四个步骤,它为我们提供了一个清晰的路线图:
- 刻画最优解的结构 (Characterize the structure of an optimal solution):
- 首先,你需要分析问题的最优解,并理解它与子问题的最优解之间存在何种关系。
- 你需要证明该问题具有“最优子结构”性质,即一个问题的最优解是由其子问题的最优解构成的。
- 递归地定义最优解的值 (Recursively define the value of an optimal solution):
- 基于第一步的分析,写出一个数学上的递归关系式(也称为状态转移方程)。
- 这个关系式应该根据子问题的解来定义原问题的解。例如,
value(problem) = f(value(subproblem_1), value(subproblem_2), ...)。
- 自底向上地计算最优解的值 (Compute the value of an optimal solution, typically in a bottom-up fashion):
- 一旦有了递归关系式,我们就可以用列表法(tabulation)来实现它。
- 创建一个或多个表格(通常是一维或二维数组)来存储子问题的解。
- 按照子问题“由小到大”的顺序,依次计算并填充表格,直到最终计算出原问题的解。
案例研究:钢条切割
这是一个经典的动态规划问题,非常适合用来演练我们的四步法。 给定一段长度为 英寸的钢条和一个价格表 (),其中 是长度为 英寸的钢条的价格。 求解如何切割钢条,使得销售总收益 最大。注意,如果长度为 的钢条不切割直接售卖的价格 足够大,那么最优解可能就是完全不切割。
价格表示例:
例如,对于一段长度为 4 的钢条,我们可以有多种切割方案:
- 不切割,收益为 。
- 切割成两段 2 英寸的,收益为 。
应用四步法求解(钢条切割)
第一步:刻画最优解的结构(钢条切割)
考虑长度为 的钢条。如果我们决定要切割,我们可以切下长度为 () 的第一段,然后还剩下一段长度为 的钢条。对于剩下的这段长度为 的钢条,我们可以继续切割,也可以不切。
这里的关键洞察是,一旦我们切下了第一段长度为 的钢条,我们对于剩余部分(长度为 )所做的决策,应该也是一个最优决策。如果我们能找到切割 的最优方案,那么将它与第一段的收益 相加,就有可能成为整个长度为 的钢条的最优解。
这就揭示了最优子结构:长度为 的钢条的最优切割方案,是由第一段的切割,以及对剩余部分的最优切割方案构成的。
第二步:递归地定义最优解的值(钢条切割)
令 表示切割长度为 的钢条所能获得的最大收益。我们可以将 表示为: 这个公式表示,最大收益是在“完全不切割”(收益 )和“切割成 和 两部分,并对 部分进行最优切割”的所有可能性中取最大值。
我们可以简化这个递归式。考虑第一刀切下长度为 的一段,我们直接卖掉它获得 ,然后对剩下的 部分进行最优切割,获得 。那么,总收益就是 。我们只需要遍历所有可能的 (从 1 到 ),就能找到最优解。 因此,递归关系式可以写作: 其中,我们定义 ,表示长度为 0 的钢条没有收益。
第三步:自底向上地计算最优解的值(钢条切割)
现在我们使用列表法,自底向上地计算 。我们创建一个数组 r[0...n] 来存储长度为 的钢条的最优解。
伪代码:
|BOTTOM-UP-CUT-ROD(p, n) # 创建一个数组 r 来存储最大收益 let r[0...n] be a new array r[0] = 0 # 长度为 0 的钢条收益为 0 # 外层循环,依次求解长度 j = 1, 2, ..., n 的最优解 for j = 1 to n max_val = -∞ # 内层循环,尝试所有可能的第一刀切割长度 i for i = 1 to j max_val = max(max_val, p[i] + r[j - i]) r[j] = max_val
示例演练 (n=4):
假设价格表 p 如上。我们来填充收益表 r,如下表所示:
最终返回 r[4] = 10,与我们之前的分析一致。
第四步:构造一个最优解(钢条切割)
上面的算法只给出了最大收益值,但没有告诉我们如何切割。为了得到切割方案,我们需要扩展算法,额外记录每一步的“最优决策”。
我们引入一个额外的数组 s[1...n],其中 s[j] 存储的是切割长度为 j 的钢条时,第一段的最优切割长度。
伪代码:
|EXTENDED-BOTTOM-UP-CUT-ROD(p, n) let r[0...n] and s[1...n] be new arrays r[0] = 0 for j = 1 to n max_val = -∞ best_cut = -1 for i = 1 to j if p[i] + r[j - i]
运行这个扩展算法后,我们会得到收益表 r 和决策表 s。例如,对于我们的价格表,计算到 n=10 时,得到的 s 表可能是:
有了决策表 s,我们就可以通过一个简单的回溯过程来打印出切割方案(伪代码):
|PRINT-CUT-ROD-SOLUTION(s, n) while n > 0 print s[n] # 打印出第一段的切割长度 n = n - s[n] # 更新剩余钢条的长度
通过这四个步骤,我们不仅找到了问题的最优解值,还成功地重构出了最优解本身。这是解决动态规划问题的完整流程。
案例研究:最长公共子序列 (LCS)
最长公共子序列问题是另一个动态规划的经典应用,在生物信息学(如 DNA 序列比对)和版本控制系统(如 diff 命令)等领域有着广泛的应用。
首先,我们需要理解“子序列”(subsequence)的概念。给定一个序列 ,另一个序列 是 的一个子序列,如果存在一个严格递增的下标序列 of 使得对于所有的 ,都有 。 简单来说,子序列就是从原序列中删除零个或多个元素后得到的序列。它。 例如,对于序列 , 是它的一个子序列,但 不是。
最长公共子序列(Longest Common Subsequence, LCS)问题:给定两个序列 和 ,找到它们共有的、长度最长的子序列。
例如,如果 且 ,那么 是它们的一个最长公共子序列,长度为 4。 也是一个,LCS 可能不唯一。
应用四步法求解(LCS)
第一步:刻画最优解的结构(LCS)
令 和 为两个序列,令 为它们的任意一个 LCS。 我们可以观察 和 的最后一个元素来分析 LCS 的最优子结构:
-
如果 :如果两个序列的最后一个元素相同,那么这个共同的元素必然是其 LCS 的最后一个元素。为什么?如果不是,我们可以将这个共同元素添加到 LCS 的末尾,得到一个更长的公共子序列,这与 LCS 的定义矛盾。因此,如果 ,那么 ,并且 (Z的前k-1个元素)是 (X的前m-1个元素)和 的一个 LCS。
因此,当 时,LCS 要么是 ,要么是 ,具体是哪一个,取决于哪个更长。
这清晰地揭示了 LCS 问题的最优子结构。一个大问题的解依赖于更小子问题的解。
第二步:递归地定义最优解的值(LCS)
令 表示序列 和 的 LCS 的。根据上面的分析,我们可以得出如下的递归关系式:
第三步:自底向上地计算最优解的值(LCS)
我们可以使用一个二维表格 c[0...m, 0...n] 来存储 LCS 的长度。为了方便第四步重构解,我们通常还会使用一个辅助表格 b[1...m, 1...n],用于记录计算每个 时所做的“选择”。我们用 "↖" 表示选择了 ,用 "↑" 表示选择了 ,用 "←" 表示选择了 。
伪代码:
|LCS-LENGTH(X, Y) m = X.length n = Y.length let b[1...m, 1...n] and c[0...m, 0...n] be new tables # 初始化边界 for i = 0 to m c[i, 0] = 0 for j = 0 to n c[0, j] = 0 # 填充表格 for
示例演练: ,
计算完成后,得到的 c 和 b 表格如下所示 (只显示 b 表中的箭头):
表格右下角的 c[7, 6] = 4 就是 LCS 的长度。
第四步:构造一个最优解(LCS)
有了记录决策的 b 表,我们可以从 b[m, n] 开始,沿着箭头方向回溯,轻松地构造出 LCS。
当我们遇到 "↖" 时,意味着 和 是 LCS 的一部分,我们记录下这个字符,然后移动到 b[i-1, j-1]。
这个过程一直持续到我们到达表格的边界(i=0 或 j=0)。
伪代码:
|PRINT-LCS(b, X, i, j) if i == 0 or j == 0 return if b[i, j] == "↖" PRINT-LCS(b, X, i - 1, j - 1) print X[i] else if b[i, j] == "↑" PRINT-LCS(b, X, i - 1, j) else PRINT
示例回溯:
从 b[7, 6] 开始:
b[7, 6]是 "↑",移动到b[6, 6]。b[6, 6]是 "↖",意味着X[6]=A是 LCS 的一部分。递归调用PRINT-LCS(b, X, 5, 5),之后打印 'A'。b[5, 5]是 "↑",移动到b[4, 5]。b[4, 5]是 "↖",意味着X[4]=B是 LCS 的一部分。递归调用PRINT-LCS(b, X, 3, 4),之后打印 'B'。b[3, 4]是 "←",移动到b[3, 3]。b[3, 3]是 "↖",意味着X[3]=C是 LCS 的一部分。递归调用PRINT-LCS(b, X, 2, 2),之后打印 'C'。b[2, 2]是 "←",移动到b[2, 1]。b[2, 1]是 "↖",意味着X[2]=B是 LCS 的一部分。递归调用PRINT-LCS(b, X, 1, 0),之后打印 'B'。i=1, j=0,递归终止。
将打印的字符反向(因为递归是反向打印的),我们得到 B C B A,这正是长度为 4 的一个最长公共子序列。
可视化演示
一个“听起来很厉害”的名字
动态规划是由美国数学家理查德·贝尔曼(Richard Bellman)在 20 世纪 50 年代发明的。它最初被应用于解决多阶段决策过程的优化问题,这是运筹学领域的一个核心课题。 关于“动态规划”这个名字的由来,有一段有趣的轶事。贝尔曼在他 1984 年的自传中解释了为什么他要选择一个听起来如此“高深莫测”的名字。 当时,他在为美国空军资助的兰德公司工作,他的上司对数学研究这个词本身抱有反感。为了让自己的研究项目听起来更重要、更不容易被拒绝,贝尔曼精心挑选了词语。
- 他选择 “规划”(Programming) 是因为它听起来很正面,意指“计划”或“决策”,并且当时线性规划(Linear Programming)是一个备受推崇的领域。
- 他选择 “动态”(Dynamic) 是因为它能准确地描述问题的时间多变性,而且这个词听起来总是比“静态”更吸引人。
贝尔曼开玩笑说,这个名字的另一个好处是,它很难给出一个精确的、一句话的定义,这使得项目更难被外行主管轻易地否定。 最终,这个为了“包装”研究项目而创造的名字,成为了计算机科学和运筹学中最强大的算法思想之一的代名词,并一直沿用至今。
小练习
-
假设你正在爬楼梯。需要 n 阶才能到达楼顶。每次你可以爬 1 或 2 个台阶。问:有多少种不同的方法可以爬到楼顶?
-
给定不同面额的硬币 coins 和一个总金额 amount,编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
|输入:coins = [1, 2, 5], amount = 11 输出:3 解释:11 = 5 + 5 + 1
- 给定一个整数数组 nums,找到其中最长严格递增子序列的长度。
|输入:nums = [10, 9, 2, 5, 3, 7, 101, 18] 输出:4 解释:最长递增子序列是 [2, 5, 7, 101],因此长度为 4。
- 有 n 个物品,第 i 个物品的重量是 weight[i],价值是 value[i]。现在有一个容量为 W 的背包,问:在不超过背包容量的前提下,能装入背包的物品的最大价值是多少?
|输入:weight = [2, 1, 3, 2], value = [12, 10, 20, 15], W = 5 输出:37 解释:选择物品 0, 1, 3,总重量 = 2 + 1 + 2 = 5,总价值 = 12 + 10 + 15 = 37
- 给定一个字符串 s,找到 s 中最长的回文子串。
|输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。