快速排序

快速排序（Quicksort）是由英国计算机科学家 Tony Hoare 于 1959 年提出的一种高效的排序算法。作为分治算法的典型代表，快速排序在理论和实践中都占据着重要地位。 该算法被广泛采用于各种编程语言的标准库实现中，包括 C++ 的 std::sort、Java 的 Arrays.sort()、以及 Python 的 sorted() 函数，这些实现都借鉴了快速排序的核心思想。

从算法复杂度的角度来看，快速排序在最坏情况下的时间复杂度为 $\Theta(n^2)$，这一情况发生在每次分区操作都产生极度不平衡的划分时。然而，在平均情况下，快速排序展现出卓越的性能，其期望时间复杂度为 $\Theta(n \lg n)$。更重要的是，快速排序的常数因子通常比归并排序更小，这使得它在实际应用中往往具有更好的性能表现。

快速排序的一个重要特性是它是一种 原地（in-place） 排序算法，这意味着除了输入数组本身，算法只需要 $O(\lg n)$ 的额外空间，这部分空间主要用于递归调用栈。在最坏情况下，递归深度可能达到 $O(n)$，此时空间复杂度为 $O(n)$，但在平均情况下，递归深度为 $O(\lg n)$，因此平均空间复杂度为 $O(\lg n)$。

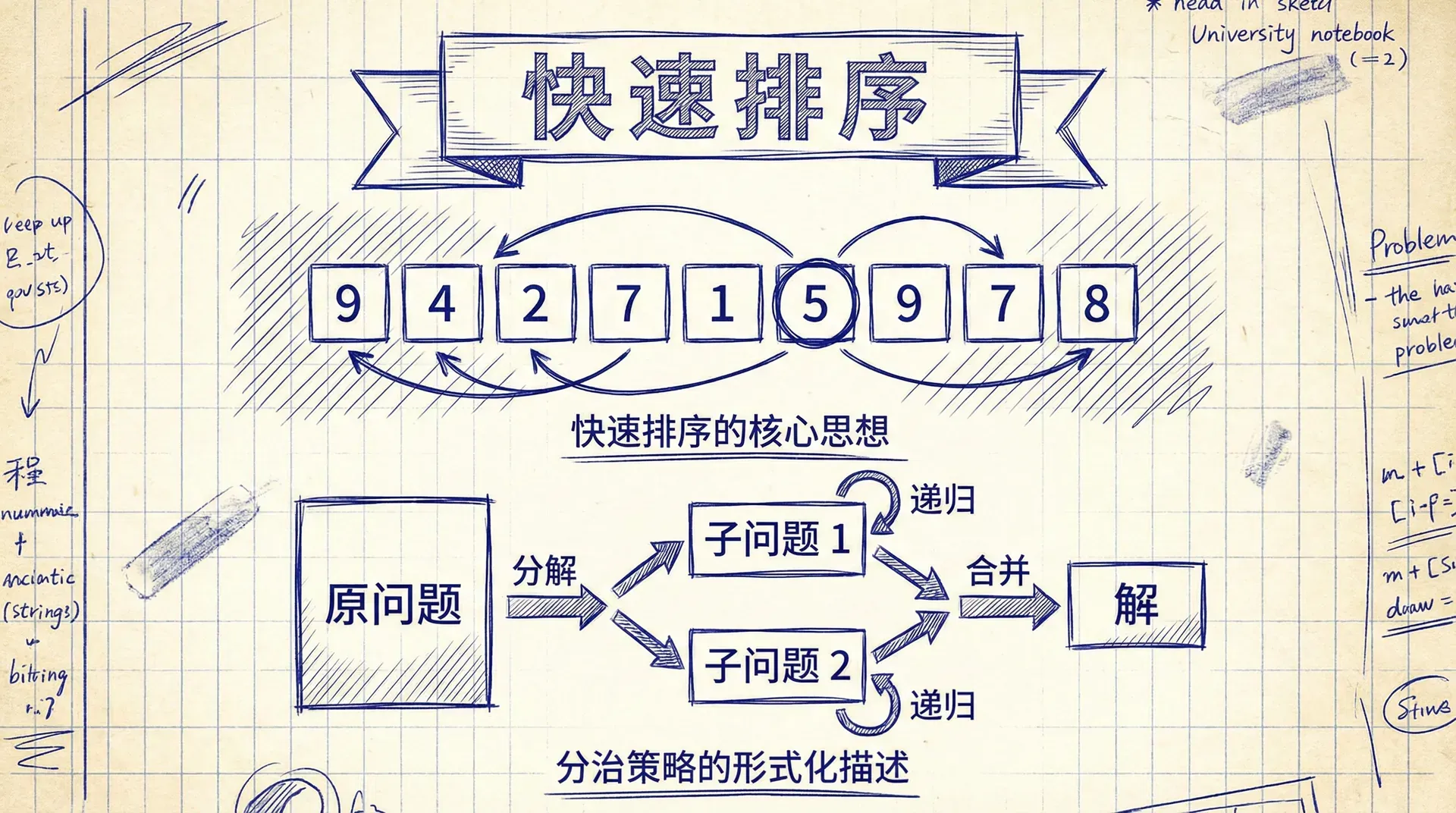
快速排序的核心思想

快速排序采用分治（divide-and-conquer）策略，但与归并排序不同，快速排序的“分”和“治”具有本质区别。在快速排序中，我们通过一个称为分区（partition） 的操作来实现分解，这个操作不仅将数组划分为两个子数组，还确保了主元（pivot）元素已经位于其在最终排序数组中的正确位置。

分治策略的形式化描述

让我们从数学的角度来理解快速排序的分治过程。给定数组 $A[p..r]$，快速排序的分治策略可以形式化地描述为：

前置条件（Precondition）：数组 $A[p..r]$ 包含 $n = r - p + 1$ 个元素。

分解（Divide）：选择一个主元元素 $x = A[q]$（其中 $q \in [p, r]$），通过分区操作将数组重新排列，使得：

• 对于所有 $i \in [p, q-1]$，有 $A[i] \leq x$
• 对于所有 $i \in [q+1, r]$，有

解决（Conquer）：递归地对子数组 $A[p..q-1]$ 和 $A[q+1..r]$ 进行快速排序。

合并（Combine）：由于分区操作已经确保了主元位于正确位置，且左右子数组在递归完成后自然有序，因此合并步骤是“免费的”，无需额外操作。

|
def quicksort(A, p, r):
    """
    快速排序主过程
    
    参数:
        A: 待排序数组
        p: 子数组起始索引
        r: 子数组结束索引
    
    后置条件:
        A[p..r] 已按非降序排列
    """
    if p < r:
        q = partition(A, p, r)  # 分区操作，返回主元最终位置
        quicksort(A, p, q - 1)  # 递归排序左子数组
        quicksort(A, q + 1, r)  # 递归排序右子数组

快速排序算法的正确性依赖于分区操作的正确性。如果我们能够证明分区操作能够正确地重新排列数组并返回主元的正确位置，那么通过数学归纳法，我们可以证明整个快速排序算法的正确性。

分区策略

分区操作是快速排序的核心，不同的分区策略在性能特征上存在显著差异。我们将在本节中详细分析两种经典的分区方案：Lomuto 分区和 Hoare 分区。

Lomuto 分区方案

Lomuto 分区方案由 Nico Lomuto 提出，是一种直观且易于理解的分区方法。该方案选择数组的最后一个元素作为主元，然后通过单次遍历将数组划分为两个区域。

算法描述：Lomuto 分区方案

Lomuto 分区维护一个重要的循环不变式（Loop Invariant），这是证明算法正确性的关键。在每次循环迭代开始时，我们保证以下性质成立：

循环不变式：对于数组 $A[p..r]$，在 for 循环的每次迭代开始时（即检查 $A[j]$ 之前），以下条件成立：

1. 对于所有 $k \in [p, i]$，有 $A[k] \leq x$（其中 $x = A[r]$ 是主元）
2. 对于所有 $k\in [i+1,j$，有

初始化：在第一次迭代之前，$i = p - 1$，$j = p$。此时区间 $[p, i]$ 为空，区间 $[i+1, j-1]$ 也为空，因此不变式在初始状态下成立。

保持：假设在第 $j$ 次迭代开始时不变式成立。我们检查 $A[j]$：

• 如果 $A[j] \leq x$，则执行 $i = i + 1$，然后交换 $A[i]$ 和 $A[j]$。交换后，$$，且区间 中的所有元素仍然 。同时，由于 （原 ）现在 ，而 （原 ）现在 （如果 ），区间 中的所有元素都 。因此不变式得以保持。

终止：当 $j = r$ 时循环终止。此时，根据不变式：

• 区间 $[p, i]$ 中的所有元素 $\leq x$
• 区间 $[i+1, r-1]$ 中的所有元素 $> x$

最后，我们将 $A[i+1]$ 与 $A[r]$ 交换，使得 $A[i+1] = x$，且所有小于等于 $x$ 的元素都在 $$ 中，所有大于 的元素都在 中。因此， 就是主元的正确位置。

|
def lomuto_partition(A, p, r):
    """
    Lomuto 分区方案
    
    参数:
        A: 数组
        p: 子数组起始索引
        r: 子数组结束索引（主元位置）
    
    返回:
        主元在分区后的最终位置
    
    时间复杂度: O(n)，其中 n = r - p + 1
    比较次数: 恰好 n - 1 次
    交换次数: 最多 n 次（当所有元素都小于等于主元时）
    """
    x = A[r]  # 选择最后一个元素作为主元
    i = p - 1  # 小于等于主元区域的右边界
    
    # 循环不变式：A[p..i] <= x, A[i+1..j-1] > x
    for j 

性能分析

Lomuto 分区的时间复杂度为 $\Theta(n)$，其中 $n = r - p + 1$。算法执行恰好 $n - 1$ 次比较操作。交换次数取决于输入数据：在最坏情况下（所有元素都小于等于主元），需要执行 $n$ 次交换；在最好情况下（所有元素都大于主元），不需要任何交换。

让我们通过一个具体例子来理解 Lomuto 分区的工作过程。考虑数组 $A = [2, 8, 7, 1, 3, 5, 6, 4]$，其中主元 $x = A[7] = 4$：

Hoare 分区方案

Hoare 分区方案由快速排序的发明者 Tony Hoare 提出，是原始快速排序算法中使用的分区方法。与 Lomuto 分区相比，Hoare 分区通常具有更好的性能特征，特别是在处理包含大量重复元素的数组时。

算法描述：Hoare 分区方案

Hoare 分区使用两个指针从数组两端向中间扫描，这种方法的核心思想是找到需要交换的元素对，从而减少不必要的操作。该算法同样维护一个重要的循环不变式：

循环不变式：在 while True 循环的每次迭代中，以下条件成立：

1. $A[p] = x$（主元，在算法开始时选择）
2. 对于所有 $k \in [p+1, i]$，有 $A[k] < x$
3. 对于所有 ，有

初始化：在第一次迭代前，$i = p - 1$，$j = r + 1$。由于区间 $[p+1, p-1]$ 和 都为空，不变式在初始状态下成立。

保持：在每次迭代中：

• 首先从右向左扫描，找到第一个 $A[j] \leq x$ 的元素
• 然后从左向右扫描，找到第一个 $A[i] \geq x$ 的元素
• 如果 $i < j$，交换 $A[i]$ 和 ，此时 且 ，不变式得以保持

终止：当 $i \geq j$ 时循环终止。此时，根据不变式，所有 $A[p+1..j]$ 中的元素都 $\leq x$，所有 $A[j+1..r]$ 中的元素都 。注意， 可能不在其最终位置，但 是划分点，使得 且 。

|
def hoare_partition(A, p, r):
    """
    Hoare 分区方案
    
    参数:
        A: 数组
        p: 子数组起始索引（主元位置）
        r: 子数组结束索引
    
    返回:
        划分点 j，使得 A[p..j] <= x 且 A[j+1..r] >= x
    
    时间复杂度: O(n)
    比较次数: 最多 n + 1 次
    交换次数: 通常比 Lomuto 分区更少
    """
    x = A[p]  # 选择第一个元素作为主元
    i = p - 1
    j = r + 1
    

性能对比分析

Hoare 分区与 Lomuto 分区在性能上存在显著差异。首先，在交换次数方面，Hoare 分区通常执行更少的交换操作，因为它在找到需要交换的元素对时才进行交换，而 Lomuto 分区可能会对已经正确位置的元素进行不必要的交换。

其次，在处理包含大量重复元素的数组时，Hoare 分区表现更好。在 Lomuto 分区中，所有等于主元的元素都会被交换到左侧，这可能导致大量的交换操作。而在 Hoare 分区中，等于主元的元素可以被分散到两侧，从而减少交换次数。

然而，需要注意的是，Hoare 分区返回的划分点 $j$ 并不一定是主元的最终位置，这与 Lomuto 分区不同。在 Lomuto 分区中，返回的位置就是主元的最终位置，而在 Hoare 分区中，主元 $A[p]$ 可能位于划分点 $j$ 的任意一侧。

时间复杂度分析

快速排序的时间复杂度分析是算法分析中的一个经典问题。我们将在本节中详细分析最坏情况、最好情况和平均情况下的时间复杂度，并给出严格的数学证明。

最坏情况：$\Theta(n^2)$

最坏情况发生在每次分区操作都产生极度不平衡的划分时。具体而言，如果每次分区都将数组划分为一个包含 $n-1$ 个元素的子数组和一个空子数组，那么快速排序的性能会严重退化。

递推关系：假设 $T(n)$ 表示对 $n$ 个元素进行快速排序的最坏情况时间复杂度。在最坏情况下，我们有： $T(n) = T(n-1) + T(0) + \Theta(n) = T(n-1) + \Theta(n)$

其中 $T(0) = \Theta(1)$ 表示对空数组排序的常数时间。

求解递推关系：通过展开递推关系，我们得到： $T(n) = T(n-1) + \Theta(n) = T(n-2) + \Theta(n-1) + \Theta(n) = \cdots = T(1) + \sum_{i=2}^{n} \Theta(i)$

由于 $\sum_{i=2}^{n} i = \frac{n(n+1)}{2} - 1 = \Theta(n^2)$，我们有：

典型场景：最坏情况的一个典型例子是输入数组已经按升序或降序排列。例如，对于已排序数组 $[1, 2, 3, 4, 5]$，如果每次选择最后一个元素作为主元，那么每次分区都会产生 $[1, 2, 3, 4]$ 和 $[]$ 的划分，导致 $\Theta(n^2)$ 的时间复杂度。

最好情况：$\Theta(n \lg n)$

最好情况发生在每次分区操作都产生完全平衡的划分时，即每次都将数组划分为两个大小大致相等的子数组。

递推关系：在最好情况下，我们有： $T(n) = 2T(n/2) + \Theta(n)$

这个递推关系与归并排序相同。

求解递推关系：根据主定理（Master Theorem），对于 $T(n) = aT(n/b) + f(n)$，其中 $a = 2$，$b = 2$，。由于 ，我们处于情况 2，因此：

平均情况：$\Theta(n \lg n)$

快速排序的平均情况分析是算法分析中的一个重要结果。关键在于理解，即使分区不是完全平衡的，只要不是极度不平衡，快速排序仍然能够保持 $\Theta(n \lg n)$ 的时间复杂度。

平衡划分的容忍度：考虑一个 9:1 的划分，即一个子数组包含 $9n/10$ 个元素，另一个包含 $n/10$ 个元素。此时的递推关系为： $T(n) = T(9n/10) + T(n/10) + \Theta(n)$

通过递归树方法，我们可以证明这个递推关系的解仍然是 $\Theta(n \lg n)$。递归树的深度为 $\log_{10/9} n = \Theta(\lg n)$，每一层的总代价为 $\Theta(n)$，因此总代价为 。

更一般的分析：实际上，对于任何常数比例的划分（如 99:1），只要比例是常数，快速排序的时间复杂度仍然是 $\Theta(n \lg n)$。这是因为递归树的深度仍然是 $\Theta(\lg n)$，只是底数不同。

概率分析：如果我们假设所有可能的划分都是等概率的，那么平均情况下，划分点会接近数组的中间位置。通过概率分析，我们可以证明快速排序的期望时间复杂度为 $\Theta(n \lg n)$。具体而言，期望的比较次数约为 $2n \ln n \approx 1.39n \lg n$，这比归并排序的 $n \lg n$ 略多，但由于快速排序的常数因子更小，实际性能往往更好。

随机化快速排序

为了克服最坏情况下的性能退化问题，我们可以采用随机化策略。随机化快速排序通过在每次分区时随机选择主元，从而以高概率避免最坏情况的发生。

随机化策略

随机化快速排序的核心思想是：通过随机选择主元，我们打破了输入数据的顺序性，使得算法对输入数据的分布不敏感。即使输入是已排序的数组，随机化后的算法仍然能够以高概率产生平衡的划分。

算法实现：随机化快速排序的实现非常简单，我们只需要在分区之前随机选择一个元素作为主元，然后将其交换到分区函数期望的位置（对于 Lomuto 分区，交换到最后一个位置；对于 Hoare 分区，交换到第一个位置）。

|
import random
 
def randomized_partition(A, p, r):
    """
    随机化分区操作
    
    通过随机选择主元，避免最坏情况的发生
    """
    i = random.randint(p, r)  # 在 [p, r] 范围内随机选择索引
    A[r], A[i] = A[i], A[r]  # 将随机主元交换到最后一个位置
    return lomuto_partition(A, p, r)
 
def randomized_quicksort(A, p, r):
    """
    随机化快速排序
    
    期望时间复杂度: O(n lg n)
    最坏情况时间复杂度: O(n²)（概率极低）
    """
    if p < r:

期望时间复杂度分析

随机化快速排序的期望时间复杂度分析是概率算法分析中的一个经典结果。关键在于理解，随机选择主元使得每个元素成为划分点的概率相等。

关键引理：在随机化快速排序中，对于任意两个元素 $A[i]$ 和 $A[j]$（其中 $i < j$），$A[i]$ 和 $A[j]$ 在算法执行过程中最多比较一次。而且， 和 被比较当且仅当在包含 和 的子数组中， 或 被选为主元。

概率计算：考虑包含 $A[i]$ 和 $A[j]$ 的最小子数组。该子数组包含 $j - i + 1$ 个元素。$A[i]$ 和 $A[j]$ 被比较的概率等于 或 在该子数组中被选为主元的概率，即 。

期望比较次数：设 $X_{ij}$ 为指示随机变量，当 $A[i]$ 和 $A[j]$ 被比较时 $X_{ij} = 1$，否则 。总的比较次数为：

期望比较次数为： $E[X] = E\left[\sum_{i=1}^{n-1} \sum_{j=i+1}^{n} X_{ij}\right] = \sum_{i=1}^{n-1} \sum_{j=i+1}^{n} E[X_{ij}] = \sum_{i=1}^{n-1} \sum_{j=i+1}^{n} \frac{2}{j-i+1}$

通过变量替换 $k = j - i$，我们得到： $E[X] = \sum_{i=1}^{n-1} \sum_{k=1}^{n-i} \frac{2}{k+1} < \sum_{i=1}^{n-1} \sum_{k=1}^{n} \frac{2}{k} = 2(n-1) \sum_{k=1}^{n} \frac{1}{k}$

由于调和级数 $H_n = \sum_{k=1}^{n} \frac{1}{k} = \Theta(\lg n)$，我们有：

类似地，我们可以证明 $E[X] = \Omega(n \lg n)$，因此 $E[X] = \Theta(n \lg n)$。

由于分区操作的时间复杂度与比较次数成正比，随机化快速排序的期望时间复杂度为 $\Theta(n \lg n)$。

三路快速排序

当输入数组包含大量重复元素时，传统的快速排序算法可能会因为频繁的重复比较而导致效率下降。三路快速排序（Three-way Quicksort）通过将数组划分为三个部分来优化这一情况：小于主元的部分、等于主元的部分和大于主元的部分。

算法思想

三路快速排序的核心思想是：在分区过程中，我们将所有等于主元的元素集中到数组的中间区域，这样在递归调用时，我们只需要对小于主元和大于主元的两个子数组进行排序，而无需处理等于主元的元素。这种方法在处理包含大量重复元素的数组时特别有效。

时间复杂度优势：当数组中所有元素都相等时，三路快速排序只需要一次遍历就能完成排序，时间复杂度为 $\Theta(n)$，而传统的快速排序仍然需要 $\Theta(n^2)$ 的时间。

算法实现

三路快速排序的分区操作维护三个区域：

• $A[p..lt-1]$：所有小于主元的元素
• $A[lt..gt]$：所有等于主元的元素
• $A[gt+1..r]$：所有大于主元的元素

其中 $lt$ 是小于区域的右边界，$gt$ 是大于区域的左边界。

|
def three_way_quicksort(A, p, r):
    """
    三路快速排序
    
    特别适用于包含大量重复元素的数组
    当所有元素相等时，时间复杂度为 O(n)
    """
    if p < r:
        lt, gt = three_way_partition(A, p, r)
        three_way_quicksort(A, p, lt - 1)  # 递归排序小于主元的部分
        three_way_quicksort(A, gt + 1, r)  # 递归排序大于主元的部分
        # 注意：等于主元的部分已经有序，无需递归
 
def three_way_partition(A, p, r):
    """
    三路分区操作
    
    将数组划分为三个部分：< x, = x, > x

三路快速排序的时间复杂度分析需要考虑重复元素的比例。设 $d$ 为数组中不同元素的数量，$n$ 为数组的总长度。

最坏情况：当所有元素都相等时，三路快速排序只需要一次遍历，时间复杂度为 $\Theta(n)$。

一般情况：当数组中存在重复元素时，三路快速排序的性能优于传统的快速排序。具体而言，如果数组中有 $k$ 个不同的值，每个值出现 $n/k$ 次，那么三路快速排序的时间复杂度为 $O(n \lg k)$，这比传统的 $O(n \lg n)$ 更好。

平均情况：通过概率分析，我们可以证明三路快速排序的平均时间复杂度仍然为 $\Theta(n \lg n)$，但在包含大量重复元素的情况下，其常数因子通常更小。

工程实践中的优化技巧

在实际应用中，快速排序的实现通常会结合多种优化技巧，以在保持算法简洁性的同时获得更好的性能。我们将在本节中详细分析这些优化技巧及其理论基础。

小数组使用插入排序

当子数组的规模较小时，快速排序的递归开销可能会超过排序本身的开销。因此，一个常见的优化是在子数组规模小于某个阈值（通常为 10 到 20）时，切换到插入排序。

理论分析：插入排序在小规模数据上的时间复杂度为 $O(k^2)$，其中 $k$ 是子数组的大小。快速排序的递归开销包括函数调用、栈帧分配等，这些开销在小规模数据上可能占主导地位。

阈值选择：最优阈值的选择取决于具体的实现和硬件环境。通过实验，通常选择 10 到 20 之间的值。理论上，我们可以通过分析递归开销和插入排序的开销来确定最优阈值，但这需要考虑具体的实现细节和硬件特性。

|
def insertion_sort(A, p, r):
    """插入排序，用于小规模子数组"""
    for i in range(p + 1, r + 1):
        key = A[i]
        j = i - 1
        while j >= p and A[j] > key:
            A[j + 1] = A[j]
            j -= 1
        A[j 

性能提升：通过使用插入排序处理小数组，我们可以减少约 10% 到 20% 的运行时间，同时代码的复杂度增加很少。

三数取中法选择主元

三数取中法（Median-of-Three）是一种选择主元的启发式方法，通过选择数组首元素、中间元素和尾元素的中位数作为主元，可以在大多数情况下获得更平衡的划分。

算法实现：三数取中法的实现需要比较三个元素并选择中位数。为了减少比较次数，我们可以使用特定的比较序列。

|
def median_of_three(A, p, r):
    """
    三数取中法选择主元
    
    选择 A[p], A[mid], A[r] 的中位数作为主元
    并将中位数交换到 A[r-1] 位置
    """
    mid = (p + r) // 2
    
    # 对三个元素进行排序（使用特定的比较序列以最小化比较次数）
    if A[p] > A[mid]:
        A[p], A[mid] = A[mid], A[p]
    if A[p] > A[r]:
        A[p], A[r] = A[r], A[p]
    if A[mid] > A[r]:

概率分析：三数取中法能够以更高的概率产生平衡的划分。具体而言，通过选择三个元素的中位数，我们避免了选择极端值（最小值或最大值）作为主元的情况，从而提高了产生平衡划分的概率。

性能影响：虽然三数取中法增加了少量的比较和交换开销，但它通常能够减少递归深度，从而在整体上提高性能。实验表明，三数取中法可以将快速排序的性能提升约 5% 到 10%。

尾递归优化

尾递归优化是一种减少递归调用栈空间的技术。在快速排序中，我们可以通过总是先递归处理较小的子数组，然后使用迭代处理较大的子数组，来将空间复杂度从 $O(n)$（最坏情况）降低到 $O(\lg n)$。

理论基础：尾递归优化的关键在于理解递归调用栈的行为。当我们总是先处理较小的子数组时，递归栈的最大深度为 $O(\lg n)$，因为每次递归调用处理的子数组大小至少减半。

|
def tail_recursive_quicksort(A, p, r):
    """
    尾递归优化的快速排序
    
    空间复杂度: O(lg n)（最坏情况）
    通过总是先处理较小的子数组，限制递归栈深度
    """
    while p < r:
        q = partition(A, p, r)
        
        # 总是先递归处理较小的子数组
        if q - p < r - q:
            tail_recursive_quicksort(A, p, q - 1)
            p = q + 1  # 使用迭代处理较大的子数组

空间复杂度分析：在尾递归优化版本中，递归栈的最大深度等于较小子数组的递归深度。由于每次划分后，较小子数组的大小最多为原数组的一半，递归深度最多为 $\lg n$，因此空间复杂度为 $O(\lg n)$。

性能影响：尾递归优化主要影响空间复杂度，对时间复杂度的改善有限。但在内存受限的环境中，这种优化可能非常重要。

算法可视化

小练习

1. 循环不变式证明：为 Hoare 分区方案编写完整的循环不变式证明，包括初始化、保持和终止三个部分。

2. 性能实验：实现 Lomuto 分区和 Hoare 分区的快速排序，比较它们在处理不同输入（已排序、逆序、随机、包含重复元素）时的性能差异，包括比较次数和交换次数。

3. 三路快排分析：分析三路快速排序在处理包含 $k$ 个不同值、每个值出现 $n/k$ 次的数组时的时间复杂度，并给出严格的数学证明。

4. 优化组合：实现一个结合了随机化、三数取中、小数组插入排序和尾递归优化的快速排序版本，并分析各种优化技巧对性能的贡献。

5. 期望时间复杂度：使用指示随机变量的方法，严格证明随机化快速排序的期望时间复杂度为 $\Theta(n \lg n)$。

此时循环不变式成立：区间 $[p, i] = \emptyset$，区间 $[i+1, j-1] = \emptyset$。