高级树 | 自在学高级树
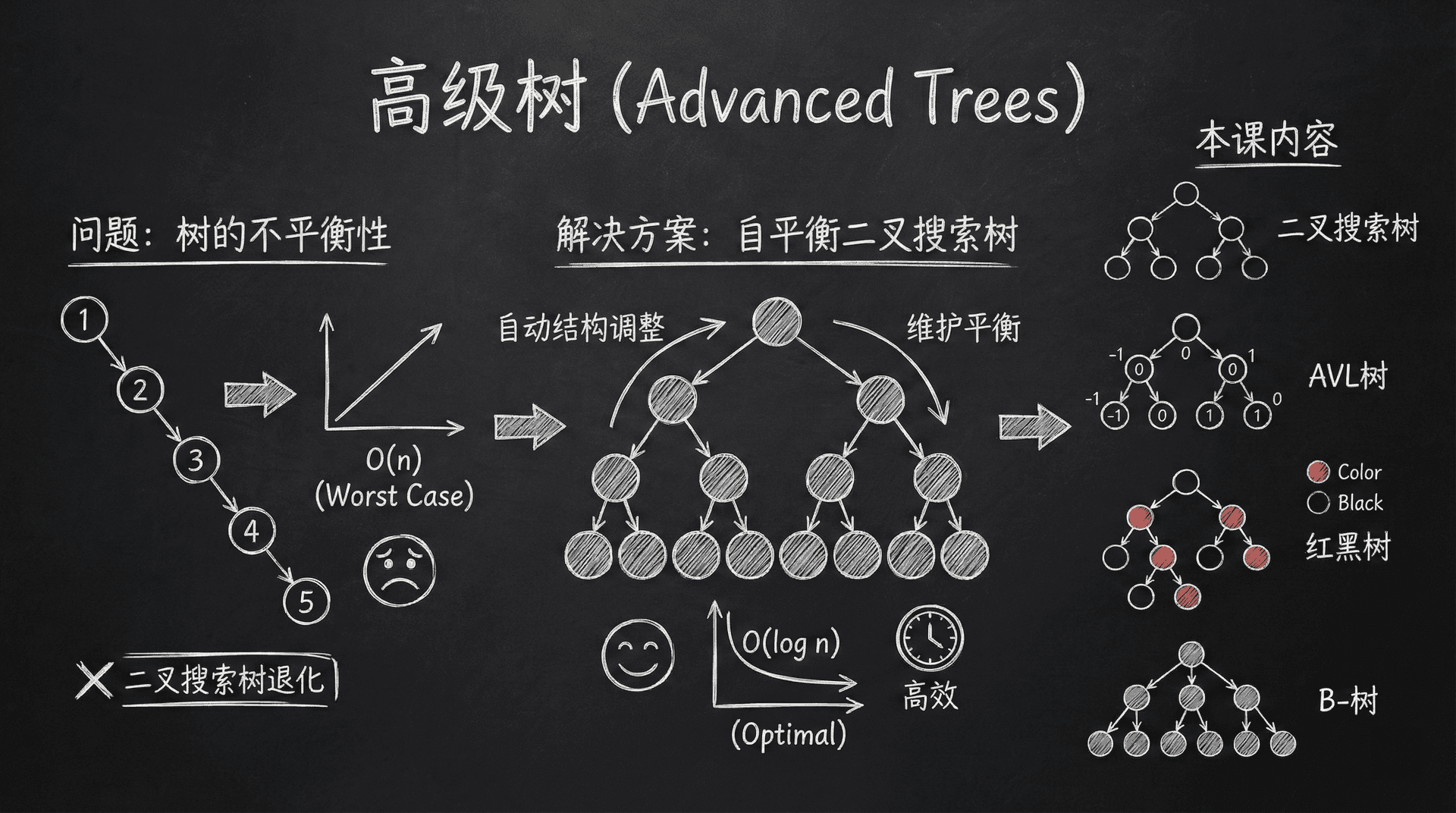
在之前的学习中,我们认识了二叉树这一基础数据结构,它通过层次化的节点组织方式为我们提供了高效的数据管理能力。然而,普通的二叉搜索树存在一个严重的性能问题:树的不平衡性。
当我们将有序序列(如 1, 2, 3, 4, 5...)依次插入一个标准的二叉搜索树时,树会退化为线性链表结构。这种退化导致树的高度从理想的 ⌈log2(n+1)⌉ 增长到 n,使得查找、插入和删除操作的时间复杂度从最优的 O(logn) 恶化到最坏的 O(n),完全丧失了二叉搜索树的分治优势。
为了解决这一根本性问题,计算机科学家们设计了一系列自平衡二叉搜索树(Self-Balancing Binary Search Trees)。这些数据结构通过维护特定的结构不变性(structural invariants),在每次插入或删除操作后自动进行结构调整,确保树的高度始终保持在 O(logn) 的量级,从而保证所有基本操作的时间复杂度为 O(logn)。
这节课,我们将系统学习四种重要的自平衡树结构:二叉搜索树(作为基础)、AVL树、红黑树和B-树,深入理解它们的设计原理、平衡维护机制以及在不同应用场景下的性能特征。
二叉搜索树 (Binary Search Tree, BST)
在学习自平衡树结构之前,我们需要深入理解二叉搜索树(BST)这一基础数据结构。虽然BST本身不具备自平衡能力,但它所遵循的BST不变性(BST Invariant) 是所有自平衡树结构的理论基础。
BST 不变性定义
二叉搜索树必须满足以下BST不变性:
对于树中的任意节点 v,设其存储的键值为 k(v),则:
- 左子树不变性:对于 v 的左子树中的任意节点 u,有 k(u)<k(v)
- 右子树不变性:对于 v 的右子树中的任意节点 w,有
这一不变性确保了BST具有有序性(ordering property),使得我们可以通过比较操作在树中进行高效的二分查找。
BST不变性赋予了树结构高效的查找能力。查找算法从根节点开始,通过比较目标键值与当前节点键值的大小关系,决定向左子树或右子树递归搜索。每一步比较都能排除掉一半的搜索空间,这与二分查找算法的思想完全一致。在平衡的BST中,查找操作的时间复杂度为 O(logn),其中 n 为树中节点的数量。
BST 的 C++ 实现
下面我们给出一个完整的、生产级别的BST实现,包含错误处理、内存管理和完整的接口设计。
#include <iostream>
#include <functional>
#include <stdexcept>
#include <algorithm>
/**
* BST节点结构
* @tparam T 节点存储的数据类型,必须支持比较操作(<, >, ==)
*/
template <typename T>
struct Node {
T data; // 节点存储的键值
Node* left; // 左子树指针
Node* right; // 右子树指针
explicit Node(const
删除操作的算法分析
删除操作是BST中最复杂的操作,需要维护BST不变性。删除算法根据目标节点的子节点数量分为三种情况:
情况1:叶子节点删除
当目标节点 v 没有子节点时,直接将其从父节点中移除并释放内存。时间复杂度为 O(1)。
情况2:单子节点删除
当目标节点 v 只有一个子节点时,用其唯一的子节点替换 v 的位置。这一操作保持BST不变性,因为 v 的子节点必然满足BST性质。时间复杂度为 O(1)。
情况3:双子节点删除
当目标节点 v 有两个子节点时,算法采用中序后继替换策略:
- 在 v 的右子树中找到最小节点 s(中序后继),满足 s=min{u∈right(v)}
- 将 s 的键值复制到 v:
这一策略的正确性基于以下事实:
- 中序后继 s 是右子树中的最小节点,因此 s 最多只有一个右子节点
- 用 s 的值替换 v 的值后,BST不变性仍然成立
- 删除 s 的问题转化为情况1或情况2,可以高效处理
时间复杂度为 O(h),其中 h 为树高。
二叉搜索树演示
AVL树:严格平衡的自平衡二叉搜索树
AVL树(Adelson-Velsky和Landis树)是最早被提出的自平衡二叉搜索树,由G. M. Adelson-Velsky和E. M. Landis在1962年发明。AVL树通过维护严格的平衡条件,确保树的高度始终为 O(logn)。
AVL树的平衡条件
AVL树要求对于树中的任意节点 v,其**平衡因子(Balance Factor)**的绝对值不超过1。平衡因子定义为:
BF(v)=h(left(v))−h(right(v))
其中 h(⋅) 表示子树的高度。因此,AVL树的平衡条件为:
∣BF(v)∣≤1,∀v∈V
这一条件确保了AVL树的高度上界。设 Nh 表示高度为 h 的AVL树的最少节点数,则有递推关系:
Nh=Nh−1+Nh−2+
其中 N0=1,N1=2。这一递推关系与斐波那契数列相关,可以证明 h,因此AVL树的高度为 。
平衡维护机制 - 旋转操作
当插入或删除操作导致某个节点的平衡因子变为 −2 或 +2 时,AVL树通过**旋转操作(Rotation)**来恢复平衡。旋转操作在保持BST不变性的同时,调整树的结构以降低高度。
旋转操作的类型与实现
旋转操作是AVL树平衡维护的核心机制。根据不平衡节点的子节点结构,存在四种不平衡情况,对应不同的旋转策略:
1. 左-左(LL)不平衡:右旋转(Right Rotation)
当节点 v 的平衡因子为 +2,且其左子节点 u 的平衡因子为 +1 或 0 时,发生LL不平衡。此时左子树过高,需要执行右旋转。
设 u=left(v),T1、T2、 分别为 的左子树、 的右子树和 的右子树。右旋转操作将 提升为新的根节点, 成为 的右子节点, 成为 的左子树。旋转后,树的高度降低1,平衡因子得到修正。
2. 右-右(RR)不平衡:左旋转(Left Rotation)
当节点 v 的平衡因子为 −2,且其右子节点 w 的平衡因子为 −1 或 0 时,发生RR不平衡。此时右子树过高,需要执行左旋转。
设 w=right(v),T1、T2、 分别为 的左子树、 的左子树和 的右子树。左旋转操作将 提升为新的根节点, 成为 的左子节点, 成为 的右子树。
3. 左-右(LR)不平衡:先左旋子树,再右旋根节点
当节点 v 的平衡因子为 +2,但其左子节点 u 的平衡因子为 −1 时,发生LR不平衡。此时左子树的右子树过高,需要执行双旋转。
首先对 u 执行左旋转,将LR不平衡转化为LL不平衡。然后对 v 执行右旋转,恢复平衡。两次旋转的时间复杂度均为 O(1),总时间复杂度为 O(1)。
4. 右-左(RL)不平衡:先右旋子树,再左旋根节点
当节点 v 的平衡因子为 −2,但其右子节点 w 的平衡因子为 +1 时,发生RL不平衡。此时右子树的左子树过高,需要执行双旋转。
首先对 w 执行右旋转,将RL不平衡转化为RR不平衡。然后对 v 执行左旋转,恢复平衡。
旋转操作保证了AVL树在每次插入或删除后都能恢复平衡,从而维持 O(logn) 的高度。虽然严格的平衡条件使得插入和删除操作可能需要 O(logn) 次旋转,但查询操作始终保持在 O(logn) 的时间复杂度,且常数因子较小。
AVL树的C++实现
#include <iostream>
#include <algorithm>
#include <stdexcept>
/**
* AVL树节点结构
*/
struct AVLNode {
int data; // 节点存储的键值
int height; // 节点的高度(用于计算平衡因子)
AVLNode* left; // 左子树指针
AVLNode* right; // 右子树指针
explicit AVLNode(int val)
: data(val),
AVL树可视化
红黑树
红黑树是一种近似平衡的二叉搜索树,由Rudolf Bayer在1972年发明。与AVL树的严格平衡策略不同,红黑树采用放宽的平衡条件,通过颜色属性和结构约束来维持树的平衡性。这种设计使得红黑树在修改密集型应用场景中具有更好的性能表现。
红黑树的高度上界
红黑树通过约束确保最长路径长度不超过最短路径长度的2倍。设 h 为树的高度,bh 为从根节点到任意叶节点的黑高(black height)(即路径上黑色节点的数量),则有:
bh≥⌈h/2⌉
由于黑高的一致性,可以证明红黑树的高度满足:
h≤2log2(n+1)
因此,红黑树的所有基本操作时间复杂度为 O(logn),虽然常数因子略大于AVL树,但修改操作的摊销成本更低。
红黑树的性质定义
红黑树必须满足以下五个不变性质(Invariant Properties):
- 节点着色:每个节点要么是红色,要么是黑色。
- 根节点约束:根节点必须是黑色。
- 叶节点约束:所有NIL节点(外部节点)为黑色。
- 红色节点约束:红色节点的子节点必须是黑色。
- 黑高一致性:从任意节点到其后代叶节点的简单路径上,黑色节点数量相同。
红黑树结构示例
平衡维护机制
红黑树通过重新着色(Recoloring) 和旋转操作(Rotation) 来维护五个不变性质。当插入或删除操作违反红黑树性质时,算法通过以下策略修复:
插入修复策略:
插入操作将新节点着色为红色(保持性质5),然后通过以下情况修复可能的违反:
-
情况1:父节点和叔节点均为红色
将父节点和叔节点着色为黑色,祖父节点着色为红色,然后递归向上检查。
-
情况2:父节点为红色,叔节点为黑色,且新节点与父节点方向不一致
通过旋转将情况转化为情况3。
-
情况3:父节点为红色,叔节点为黑色,且新节点与父节点方向一致
将父节点着色为黑色,祖父节点着色为红色,然后执行旋转。
删除修复策略:
删除操作可能引入双重黑色节点,通过重新着色和旋转逐步向上修复,最多需要 O(logn) 次操作。
旋转操作与AVL树类似,但需要同时调整节点颜色以维护红黑树性质。
性能分析与应用场景
时间复杂度分析:
- 查找操作:O(logn),由树高上界 h≤2log2(n+1) 保证
- 插入操作:,最多需要 次重新着色和最多2次旋转
空间复杂度: O(n),每个节点需要额外的1位存储颜色信息。
实际应用:
- C++ STL:
std::map、std::set、std::multimap、std::multiset 的底层实现
- Java 集合框架:
TreeMap、TreeSet 的实现
- Linux 内核:完全公平调度器(CFS)的运行队列、虚拟内存管理
- 数据库系统:某些内存索引结构、B+树的内部节点实现
工程价值:
红黑树在插入/删除密集型场景下表现优异。虽然其查找性能的常数因子略大于AVL树,但其修改操作的摊销成本更低,且实现相对简单,这使得它成为许多实际系统中平衡二叉搜索树的首选实现。
红黑树的C++实现
#include <iostream>
#include <functional>
#include <stdexcept>
/**
* 节点颜色枚举
*/
enum class Color { RED, BLACK };
/**
* 红黑树节点结构
*/
struct RBNode {
int data; // 节点存储的键值
Color color; // 节点颜色
RBNode* left; // 左子树指针
RBNode* right; // 右子树指针
B-树
前面讨论的BST、AVL树和红黑树都是内存数据结构,假设所有数据都存储在快速访问的内存中。然而,当数据规模达到TB甚至PB级别时,数据必须存储在外部存储设备(如磁盘) 中。
磁盘I/O的性能瓶颈
磁盘访问与内存访问存在数量级的性能差异:
- 内存访问延迟:约 100 纳秒
- 磁盘访问延迟:约 10 毫秒(包括寻道时间、旋转延迟和传输时间)
这意味着一次磁盘I/O操作的时间相当于约 105 次内存访问。因此,对于外部存储数据结构,优化目标从减少比较次数转变为最小化磁盘I/O次数。
B-树的设计原理
B-树(Bayer和McCreight,1972)是一种专为外部存储设计的多路平衡搜索树。与二叉搜索树不同,B-树的每个节点可以存储多个键值和多个子节点指针,这种设计使得B-树具有以下特征:
- 高分支因子(High Branching Factor):每个内部节点有 t 到 2t 个子节点,其中 t≥2 称为B-树的最小度数(minimum degree)
- 低树高(Low Height):由于高分支因子,B-树的高度被极大压缩。对于存储 n 个键的B-树,其高度 h 满足:
h≤logt2n+1
对于典型的 t=256 的B-树,即使存储 109 条记录,树高也仅为 3-4 层。这意味着查找任意记录最多只需要 3-4 次磁盘I/O操作。
- 节点大小优化:B-树节点的大小通常设计为磁盘页大小(如4KB),使得每次磁盘读取都能获取最大量的决策信息。
B-树的结构定义
B-树必须满足以下性质:
- 节点键值数量:每个节点最多存储 2t−1 个键,最少存储 t−1 个键(根节点除外,根节点至少1个键)
- 节点子节点数量:每个内部节点最多有 2t 个子节点,最少有 t 个子节点(根节点除外)
- 有序性:节点内的键值按升序排列
- BST性质:对于节点中的键 k,其左子树的所有键小于 ,右子树的所有键大于
B-树的操作策略
查找操作:
从根节点开始,在节点内使用二分查找定位键值范围,然后递归进入相应的子节点。由于节点大小与磁盘页匹配,每次磁盘读取都能获取大量键值信息,从而最小化磁盘I/O次数。
插入操作:
采用自顶向下分裂策略:在向下遍历路径中,如果遇到满节点(2t−1 个键),先进行分裂,然后再继续插入。这确保了插入路径上的所有节点都有空间,避免了回溯操作。
删除操作:
删除操作需要处理节点键值数量不足的情况,可能涉及键值合并和重新分配,但保证最多需要 O(logtn) 次磁盘I/O。
B-树的应用
B-树及其变体(如B+树)是现代数据库系统和文件系统的核心数据结构:
- 关系型数据库:MySQL、PostgreSQL、Oracle等使用B+树作为索引结构
- 文件系统:NTFS、ext4等使用B-树变体管理文件元数据
- NoSQL数据库:MongoDB、CouchDB等使用B-树管理文档索引
B-树通过优化磁盘I/O模式,使得大规模数据管理成为可能,是现代数据系统的基石。
B-树的C++实现
#include <iostream>
#include <vector>
#include <algorithm>
#include <stdexcept>
/**
* B-树节点类
*
* 节点约束:
* - 最多存储 2t-1 个键(根节点除外)
* - 最多有 2t 个子节点
* - 内部节点至少有 t 个子节点(根节点除外)
*/
class BTreeNode {
public:
std::vector<int> keys; // 键值数组(有序)
std::vector<BTreeNode*> children; // 子节点指针数组
bool isLeaf; // 是否为叶子节点
数据结构选择指南
在实际应用中,选择合适的树结构需要综合考虑数据规模、访问模式、存储介质和性能要求。下面我们系统分析各种树结构的适用场景。
二叉搜索树的适用场景 (BST)
适用场景:
- 教学和原型开发
- 数据规模小(< 1000 个元素)
- 数据插入顺序随机
- 对性能要求不严格的场景
局限性:
- 最坏情况时间复杂度为 O(n)(退化为链表)
- 不适合生产环境
结论: BST主要用于理解树结构的基本原理,不推荐用于生产环境。
AVL树的适用场景
适用场景:
- 读密集型应用:查询操作远多于插入和删除
- 对查询性能要求极高的场景
- 数据规模中等(内存可容纳)
- 需要保证最坏情况性能的场景
性能特征:
- 查询性能最优(树高最小,常数因子小)
- 插入/删除操作可能需要 O(logn) 次旋转
- 适合静态或半静态数据集
实际应用: 某些数据库索引、内存中的有序集合(当查询频率远高于修改频率时)
红黑树的适用场景
适用场景:
- 修改密集型应用:插入和删除操作频繁
- 需要平衡的读写性能
- 通用目的的有序数据结构
- 标准库实现(如C++ STL、Java集合框架)
性能特征:
- 查询性能略逊于AVL树(树高上界为 2log2(n+1))
- 插入/删除操作的摊销成本更低
- 实现相对简单,维护成本低
实际应用: std::map、std::set、TreeMap、TreeSet、Linux内核调度器
B-树的适用场景
适用场景:
- 外部存储数据结构:数据存储在磁盘上
- 大规模数据管理(TB级及以上)
- 数据库索引和文件系统
- 需要最小化磁盘I/O的场景
性能特征:
- 通过高分支因子最小化磁盘I/O次数
- 节点大小匹配磁盘页大小(如4KB)
- 树高极低(即使存储 109 条记录,树高也仅为3-4层)
实际应用: MySQL、PostgreSQL、Oracle等数据库的索引,NTFS、ext4等文件系统
选择决策树
总结:
- 内存小规模数据 + 读多写少 → AVL树
- 内存小规模数据 + 读写平衡 → 红黑树(推荐)
- 磁盘大规模数据 → B-树或B+树
- 教学和原型 → BST(仅用于理解)
小练习
- 在一个AVL树中,节点v的左子树高度为3,右子树高度为4,平衡因子BF(v)是多少?
- 在红黑树中,如果节点v为红色,其父节点p(v)也为红色,这违反了哪条性质?
k(w)>k(v)
递归性:v 的每个子节点及其所有后代节点都必须递归地满足上述不变性 T
&
val
) :
data
(val),
left
(
nullptr
),
right
(
nullptr
) {}
};
/**
* 二叉搜索树实现
* @tparam T 元素类型,必须支持比较操作
*
* 时间复杂度:
* - 查找:O(h),其中 h 为树高,最坏情况 O(n),最好情况 O(log n)
* - 插入:O(h)
* - 删除:O(h)
*
* 空间复杂度:O(n) 用于存储节点
*/
template <typename T>
class BST {
private:
Node<T>* root; // 根节点指针
/**
* 递归插入节点
* @param node 当前子树根节点
* @param value 要插入的值
* @return 更新后的子树根节点
* @throws std::bad_alloc 当内存分配失败时
*/
Node<T>* insertRecursive(Node<T>* node, const T& value) {
if (node == nullptr) {
return new Node<T>(value);
}
if (value < node->data) {
node->left = insertRecursive(node->left, value);
} else if (value > node->data) {
node->right = insertRecursive(node->right, value);
}
// 如果 value == node->data,不插入重复值,保持BST的唯一性
return node;
}
/**
* 递归搜索节点
* @param node 当前子树根节点
* @param value 要搜索的值
* @return 如果找到返回 true,否则返回 false
*/
bool searchRecursive(const Node<T>* node, const T& value) const {
if (node == nullptr) {
return false;
}
if (value == node->data) {
return true;
}
return value < node->data
? searchRecursive(node->left, value)
: searchRecursive(node->right, value);
}
/**
* 查找子树中的最小节点(中序后继的前驱)
* @param node 子树根节点
* @return 最小节点的指针,如果子树为空返回 nullptr
*/
Node<T>* findMin(Node<T>* node) const {
if (node == nullptr) {
return nullptr;
}
while (node->left != nullptr) {
node = node->left;
}
return node;
}
/**
* 查找子树中的最大节点
* @param node 子树根节点
* @return 最大节点的指针,如果子树为空返回 nullptr
*/
Node<T>* findMax(Node<T>* node) const {
if (node == nullptr) {
return nullptr;
}
while (node->right != nullptr) {
node = node->right;
}
return node;
}
/**
* 递归删除节点
* @param node 当前子树根节点
* @param value 要删除的值
* @return 更新后的子树根节点
*
* 删除策略:
* 1. 叶子节点或单子节点:直接用子节点替换
* 2. 双子节点:用中序后继的值替换,然后递归删除中序后继节点
*/
Node<T>* removeRecursive(Node<T>* node, const T& value) {
if (node == nullptr) {
return nullptr; // 未找到要删除的节点
}
// 定位要删除的节点
if (value < node->data) {
node->left = removeRecursive(node->left, value);
} else if (value > node->data) {
node->right = removeRecursive(node->right, value);
} else {
// 找到要删除的节点
// 情况1:左子树为空
if (node->left == nullptr) {
Node<T>* temp = node->right;
delete node;
return temp;
}
// 情况2:右子树为空
else if (node->right == nullptr) {
Node<T>* temp = node->left;
delete node;
return temp;
}
// 情况3:左右子树均非空
else {
// 找到右子树中的最小节点(中序后继)
Node<T>* successor = findMin(node->right);
// 用中序后继的值替换当前节点的值
node->data = successor->data;
// 递归删除中序后继节点(该节点最多只有一个右子节点)
node->right = removeRecursive(node->right, successor->data);
}
}
return node;
}
/**
* 后序遍历释放所有节点内存
* @param node 当前子树根节点
*/
void destroyRecursive(Node<T>* node) {
if (node != nullptr) {
destroyRecursive(node->left);
destroyRecursive(node->right);
delete node;
}
}
/**
* 中序遍历,按升序访问所有节点
* @param node 当前子树根节点
* @param visit 访问函数,对每个节点调用 visit(node->data)
*/
void inorderRecursive(const Node<T>* node, std::function<void(const T&)> visit) const {
if (node != nullptr) {
inorderRecursive(node->left, visit);
visit(node->data);
inorderRecursive(node->right, visit);
}
}
/**
* 计算树的高度
* @param node 当前子树根节点
* @return 树的高度(空树高度为0)
*/
int getHeight(const Node<T>* node) const {
if (node == nullptr) {
return 0;
}
return 1 + std::max(getHeight(node->left), getHeight(node->right));
}
/**
* 验证BST不变性
* @param node 当前子树根节点
* @param minVal 允许的最小值(用于验证)
* @param maxVal 允许的最大值(用于验证)
* @return 如果满足BST性质返回 true
*/
bool isValidBST(const Node<T>* node, const T* minVal, const T* maxVal) const {
if (node == nullptr) {
return true;
}
if ((minVal != nullptr && node->data <= *minVal) ||
(maxVal != nullptr && node->data >= *maxVal)) {
return false;
}
return isValidBST(node->left, minVal, &node->data) &&
isValidBST(node->right, &node->data, maxVal);
}
// 禁用拷贝构造和赋值操作(简化实现,生产环境应实现深拷贝)
BST(const BST&) = delete;
BST& operator=(const BST&) = delete;
public:
/**
* 构造函数:创建空BST
*/
BST() : root(nullptr) {}
/**
* 析构函数:释放所有节点内存
*/
~BST() {
destroyRecursive(root);
}
/**
* 插入元素
* @param value 要插入的值
* @throws std::bad_alloc 当内存分配失败时
*/
void insert(const T& value) {
root = insertRecursive(root, value);
}
/**
* 查找元素
* @param value 要查找的值
* @return 如果找到返回 true,否则返回 false
*/
bool search(const T& value) const {
return searchRecursive(root, value);
}
/**
* 删除元素
* @param value 要删除的值
*/
void remove(const T& value) {
root = removeRecursive(root, value);
}
/**
* 中序遍历
* @param visit 访问函数
*/
void inorderTraversal(std::function<void(const T&)> visit) const {
inorderRecursive(root, visit);
}
/**
* 获取树的高度
* @return 树的高度
*/
int height() const {
return getHeight(root);
}
/**
* 验证BST不变性
* @return 如果满足BST性质返回 true
*/
bool isValid() const {
return isValidBST(root, nullptr, nullptr);
}
/**
* 检查树是否为空
* @return 如果树为空返回 true
*/
bool empty() const {
return root == nullptr;
}
};
k(v)←k(s)
1
≤
1.44log2(n+
2)−
0.328
T3
T3
height
(
1
),
left
(
nullptr
),
right
(
nullptr
) {}
};
/**
* AVL树实现
*
* 时间复杂度:
* - 查找:O(log n)
* - 插入:O(log n),最多需要 O(log n) 次旋转
* - 删除:O(log n),最多需要 O(log n) 次旋转
*
* 空间复杂度:O(n)
*/
class AVLTree {
private:
AVLNode* root;
/**
* 获取节点高度(空节点高度为0)
*/
int getHeight(const AVLNode* node) const {
return node ? node->height : 0;
}
/**
* 计算平衡因子
* @return 左子树高度 - 右子树高度
*/
int getBalanceFactor(const AVLNode* node) const {
if (node == nullptr) {
return 0;
}
return getHeight(node->left) - getHeight(node->right);
}
/**
* 更新节点高度
* 高度 = 1 + max(左子树高度, 右子树高度)
*/
void updateHeight(AVLNode* node) {
if (node != nullptr) {
node->height = 1 + std::max(
getHeight(node->left),
getHeight(node->right)
);
}
}
/**
* 右旋转:解决LL不平衡
*
* y x
* / \ / \
* x T3 => T1 y
* / \ / \
* T1 T2 T2 T3
*
* @param y 不平衡节点
* @return 旋转后的新根节点
*/
AVLNode* rotateRight(AVLNode* y) {
AVLNode* x = y->left;
AVLNode* T2 = x->right;
// 执行旋转
x->right = y;
y->left = T2;
// 更新高度(先更新子树,再更新根)
updateHeight(y);
updateHeight(x);
return x; // 返回新的根节点
}
/**
* 左旋转:解决RR不平衡
*
* x y
* / \ / \
* T1 y => x T3
* / \ / \
* T2 T3 T1 T2
*
* @param x 不平衡节点
* @return 旋转后的新根节点
*/
AVLNode* rotateLeft(AVLNode* x) {
AVLNode* y = x->right;
AVLNode* T2 = y->left;
// 执行旋转
y->left = x;
x->right = T2;
// 更新高度
updateHeight(x);
updateHeight(y);
return y; // 返回新的根节点
}
/**
* 递归插入节点
* @param node 当前子树根节点
* @param data 要插入的值
* @return 更新后的子树根节点
*/
AVLNode* insertRecursive(AVLNode* node, int data) {
// 1. 执行标准BST插入
if (node == nullptr) {
return new AVLNode(data);
}
if (data < node->data) {
node->left = insertRecursive(node->left, data);
} else if (data > node->data) {
node->right = insertRecursive(node->right, data);
} else {
return node; // 不允许重复值
}
// 2. 更新当前节点的高度
updateHeight(node);
// 3. 计算平衡因子
int balance = getBalanceFactor(node);
// 4. 根据不平衡类型执行相应的旋转
// LL情况:左子树左子节点导致不平衡
if (balance > 1 && data < node->left->data) {
return rotateRight(node);
}
// RR情况:右子树右子节点导致不平衡
if (balance < -1 && data > node->right->data) {
return rotateLeft(node);
}
// LR情况:左子树右子节点导致不平衡
if (balance > 1 && data > node->left->data) {
node->left = rotateLeft(node->left); // 先左旋左子树
return rotateRight(node); // 再右旋当前节点
}
// RL情况:右子树左子节点导致不平衡
if (balance < -1 && data < node->right->data) {
node->right = rotateRight(node->right); // 先右旋右子树
return rotateLeft(node); // 再左旋当前节点
}
return node; // 树已平衡,无需旋转
}
/**
* 验证AVL树性质
* @param node 当前子树根节点
* @return 如果满足AVL性质返回 true
*/
bool isValidAVL(const AVLNode* node) const {
if (node == nullptr) {
return true;
}
int balance = getBalanceFactor(node);
if (balance < -1 || balance > 1) {
return false; // 平衡因子超出范围
}
return isValidAVL(node->left) && isValidAVL(node->right);
}
/**
* 后序遍历释放内存
*/
void destroyRecursive(AVLNode* node) {
if (node != nullptr) {
destroyRecursive(node->left);
destroyRecursive(node->right);
delete node;
}
}
/**
* 中序遍历
*/
void inorderRecursive(const AVLNode* node,
std::function<void(int)> visit) const {
if (node != nullptr) {
inorderRecursive(node->left, visit);
visit(node->data);
inorderRecursive(node->right, visit);
}
}
// 禁用拷贝构造和赋值
AVLTree(const AVLTree&) = delete;
AVLTree& operator=(const AVLTree&) = delete;
public:
AVLTree() : root(nullptr) {}
~AVLTree() {
destroyRecursive(root);
}
/**
* 插入元素
* @param data 要插入的值
*/
void insert(int data) {
root = insertRecursive(root, data);
}
/**
* 验证AVL树性质
*/
bool isValid() const {
return isValidAVL(root);
}
/**
* 获取树的高度
*/
int height() const {
return getHeight(root);
}
/**
* 中序遍历
*/
void inorderTraversal(std::function<void(int)> visit) const {
inorderRecursive(root, visit);
}
/**
* 检查树是否为空
*/
bool empty() const {
return root == nullptr;
}
};
// 使用示例
int main() {
AVLTree avl;
// 插入数据,演示自动平衡
avl.insert(10);
avl.insert(20);
avl.insert(30); // 触发RR不平衡,执行左旋转
avl.insert(40);
avl.insert(50); // 触发RR不平衡,执行左旋转
avl.insert(25); // 触发RL不平衡,执行双旋转
// 验证AVL性质
std::cout << "AVL树是否有效: " << (avl.isValid() ? "是" : "否") << std::endl;
std::cout << "树的高度: " << avl.height() << std::endl;
// 中序遍历(输出有序序列)
std::cout << "中序遍历: ";
avl.inorderTraversal([](int val) { std::cout << val << " "; });
std::cout << std::endl;
return 0;
}
O
(
log
n
)
删除操作:O(logn),最多需要 O(logn) 次重新着色和最多3次旋转 RBNode* parent; // 父节点指针(用于旋转和修复)
explicit RBNode(int val)
: data(val), color(Color::RED),
left(nullptr), right(nullptr), parent(nullptr) {}
};
/**
* 红黑树实现
*
* 时间复杂度:所有操作均为 O(log n)
* 空间复杂度:O(n)
*/
class RedBlackTree {
private:
RBNode* root; // 根节点指针
RBNode* NIL; // 哨兵节点(代表所有NIL叶子节点)
/**
* 左旋转
*
* x y
* / \ / \
* T1 y => x T3
* / \ / \
* T2 T3 T1 T2
*/
void rotateLeft(RBNode* x) {
RBNode* y = x->right;
x->right = y->left;
if (y->left != NIL) {
y->left->parent = x;
}
y->parent = x->parent;
if (x->parent == nullptr) {
root = y;
} else if (x == x->parent->left) {
x->parent->left = y;
} else {
x->parent->right = y;
}
y->left = x;
x->parent = y;
}
/**
* 右旋转
*
* y x
* / \ / \
* x T3 => T1 y
* / \ / \
* T1 T2 T2 T3
*/
void rotateRight(RBNode* y) {
RBNode* x = y->left;
y->left = x->right;
if (x->right != NIL) {
x->right->parent = y;
}
x->parent = y->parent;
if (y->parent == nullptr) {
root = x;
} else if (y == y->parent->right) {
y->parent->right = x;
} else {
y->parent->left = x;
}
x->right = y;
y->parent = x;
}
/**
* 插入后修复红黑树性质
* 修复违反的性质4(红色节点的子节点必须是黑色)
*
* @param z 新插入的节点
*/
void insertFixup(RBNode* z) {
while (z->parent != nullptr && z->parent->color == Color::RED) {
if (z->parent == z->parent->parent->left) {
// 父节点是祖父节点的左子节点
RBNode* uncle = z->parent->parent->right;
if (uncle->color == Color::RED) {
// 情况1:叔节点为红色
// 重新着色:父节点和叔节点变黑,祖父节点变红
z->parent->color = Color::BLACK;
uncle->color = Color::BLACK;
z->parent->parent->color = Color::RED;
z = z->parent->parent; // 向上检查
} else {
// 情况2和3:叔节点为黑色
if (z == z->parent->right) {
// 情况2:z是右子节点,转换为情况3
z = z->parent;
rotateLeft(z);
}
// 情况3:z是左子节点
z->parent->color = Color::BLACK;
z->parent->parent->color = Color::RED;
rotateRight(z->parent->parent);
}
} else {
// 对称情况:父节点是祖父节点的右子节点
RBNode* uncle = z->parent->parent->left;
if (uncle->color == Color::RED) {
z->parent->color = Color::BLACK;
uncle->color = Color::BLACK;
z->parent->parent->color = Color::RED;
z = z->parent->parent;
} else {
if (z == z->parent->left) {
z = z->parent;
rotateRight(z);
}
z->parent->color = Color::BLACK;
z->parent->parent->color = Color::RED;
rotateLeft(z->parent->parent);
}
}
}
// 确保根节点为黑色(性质2)
root->color = Color::BLACK;
}
/**
* 验证红黑树性质
* @param node 当前节点
* @param blackCount 当前路径的黑高
* @param pathBlackCount 参考路径的黑高(用于验证性质5)
* @return 如果满足所有性质返回 true
*/
bool isValidRB(const RBNode* node, int blackCount, int& pathBlackCount) const {
if (node == NIL) {
if (pathBlackCount == -1) {
pathBlackCount = blackCount;
}
return blackCount == pathBlackCount; // 验证性质5
}
// 验证性质4:红色节点的子节点必须是黑色
if (node->color == Color::RED) {
if ((node->left != NIL && node->left->color == Color::RED) ||
(node->right != NIL && node->right->color == Color::RED)) {
return false;
}
}
// 递归验证左右子树
int nextBlackCount = blackCount +
(node->color == Color::BLACK ? 1 : 0);
return isValidRB(node->left, nextBlackCount, pathBlackCount) &&
isValidRB(node->right, nextBlackCount, pathBlackCount);
}
/**
* 后序遍历释放内存
*/
void destroyRecursive(RBNode* node) {
if (node != NIL && node != nullptr) {
destroyRecursive(node->left);
destroyRecursive(node->right);
delete node;
}
}
/**
* 中序遍历
*/
void inorderRecursive(const RBNode* node,
std::function<void(int, Color)> visit) const {
if (node != NIL) {
inorderRecursive(node->left, visit);
visit(node->data, node->color);
inorderRecursive(node->right, visit);
}
}
// 禁用拷贝构造和赋值
RedBlackTree(const RedBlackTree&) = delete;
RedBlackTree& operator=(const RedBlackTree&) = delete;
public:
/**
* 构造函数:初始化空树和NIL节点
*/
RedBlackTree() {
NIL = new RBNode(0);
NIL->color = Color::BLACK; // NIL节点为黑色(性质3)
NIL->left = NIL->right = NIL->parent = nullptr;
root = NIL;
}
/**
* 析构函数:释放所有节点内存
*/
~RedBlackTree() {
destroyRecursive(root);
delete NIL;
}
/**
* 插入节点
* @param data 要插入的值
*/
void insert(int data) {
RBNode* newNode = new RBNode(data);
newNode->left = newNode->right = NIL;
RBNode* parent = nullptr;
RBNode* current = root;
// 标准BST插入:找到插入位置
while (current != NIL) {
parent = current;
if (data < current->data) {
current = current->left;
} else if (data > current->data) {
current = current->right;
} else {
// 不允许重复值
delete newNode;
return;
}
}
newNode->parent = parent;
if (parent == nullptr) {
root = newNode; // 插入根节点
} else if (data < parent->data) {
parent->left = newNode;
} else {
parent->right = newNode;
}
// 修复红黑树性质
insertFixup(newNode);
}
/**
* 验证红黑树性质
* @return 如果满足所有性质返回 true
*/
bool isValid() const {
if (root == NIL) {
return true; // 空树满足所有性质
}
// 验证性质2:根节点为黑色
if (root->color != Color::BLACK) {
return false;
}
int pathBlackCount = -1;
return isValidRB(root, 0, pathBlackCount);
}
/**
* 中序遍历
* @param visit 访问函数,参数为 (键值, 颜色)
*/
void inorderTraversal(std::function<void(int, Color)> visit) const {
inorderRecursive(root, visit);
}
/**
* 检查树是否为空
*/
bool empty() const {
return root == NIL;
}
};
// 使用示例
int main() {
RedBlackTree rbt;
// 插入数据
rbt.insert(10);
rbt.insert(20);
rbt.insert(30);
rbt.insert(15);
rbt.insert(25);
rbt.insert(5);
// 验证红黑树性质
std::cout << "红黑树是否有效: " << (rbt.isValid() ? "是" : "否") << std::endl;
// 中序遍历
std::cout << "中序遍历: ";
rbt.inorderTraversal([](int val, Color color) {
std::cout << val << "(" << (color == Color::RED ? "R" : "B") << ") ";
});
std::cout << std::endl;
return 0;
}
i
平衡性:所有叶节点位于同一层 int minDegree; // 最小度数 t
/**
* 构造函数
* @param degree 最小度数 t
* @param leaf 是否为叶子节点
*/
BTreeNode(int degree, bool leaf)
: minDegree(degree), isLeaf(leaf) {
keys.reserve(2 * degree - 1);
children.reserve(2 * degree);
}
/**
* 在非满节点中插入键值
* @param key 要插入的键值
*/
void insertNonFull(int key) {
int i = static_cast<int>(keys.size()) - 1;
if (isLeaf) {
// 叶子节点:直接插入并保持有序
keys.push_back(0); // 扩展空间
while (i >= 0 && keys[i] > key) {
keys[i + 1] = keys[i];
i--;
}
keys[i + 1] = key;
} else {
// 内部节点:找到应该插入的子节点
while (i >= 0 && keys[i] > key) {
i--;
}
i++;
// 如果子节点已满,先分裂
if (children[i]->keys.size() == 2 * minDegree - 1) {
splitChild(i, children[i]);
// 分裂后,中间键值提升到当前节点
if (keys[i] < key) {
i++;
}
}
children[i]->insertNonFull(key);
}
}
/**
* 分裂满的子节点
*
* 将满节点(2t-1个键)分裂为两个节点(各t-1个键),
* 中间键值提升到父节点
*
* @param index 子节点在children数组中的索引
* @param fullChild 要分裂的满子节点
*/
void splitChild(int index, BTreeNode* fullChild) {
// 创建新节点(右半部分)
BTreeNode* newChild = new BTreeNode(fullChild->minDegree,
fullChild->isLeaf);
// 移动后半部分键值(索引 t 到 2t-2)
for (int j = 0; j < minDegree - 1; j++) {
newChild->keys.push_back(fullChild->keys[j + minDegree]);
}
// 如果不是叶子节点,移动后半部分子节点指针
if (!fullChild->isLeaf) {
for (int j = 0; j < minDegree; j++) {
newChild->children.push_back(fullChild->children[j + minDegree]);
}
fullChild->children.resize(minDegree);
}
// 提取中间键值(索引 t-1)
int midKey = fullChild->keys[minDegree - 1];
fullChild->keys.resize(minDegree - 1);
// 在当前节点中插入中间键值和新子节点
children.insert(children.begin() + index + 1, newChild);
keys.insert(keys.begin() + index, midKey);
}
/**
* 搜索键值
* @param key 要搜索的键值
* @return 如果找到返回 true
*/
bool search(int key) {
// 在节点内查找键值位置
size_t i = 0;
while (i < keys.size() && key > keys[i]) {
i++;
}
// 如果找到键值
if (i < keys.size() && keys[i] == key) {
return true;
}
// 如果是叶子节点且未找到,返回false
if (isLeaf) {
return false;
}
// 在相应的子节点中继续搜索
return children[i]->search(key);
}
/**
* 中序遍历(按升序输出所有键值)
* @param visit 访问函数
*/
void traverse(std::function<void(int)> visit) {
size_t i;
for (i = 0; i < keys.size(); i++) {
// 先遍历左子树
if (!isLeaf) {
children[i]->traverse(visit);
}
// 访问当前键值
visit(keys[i]);
}
// 遍历最后一个子树
if (!isLeaf) {
children[i]->traverse(visit);
}
}
/**
* 析构函数:递归释放所有子节点
*/
~BTreeNode() {
if (!isLeaf) {
for (BTreeNode* child : children) {
delete child;
}
}
}
// 禁用拷贝构造和赋值
BTreeNode(const BTreeNode&) = delete;
BTreeNode& operator=(const BTreeNode&) = delete;
};
/**
* B-树类
*
* 时间复杂度:
* - 查找:O(log_t n),其中 t 为最小度数
* - 插入:O(log_t n)
* - 删除:O(log_t n)
*
* 空间复杂度:O(n)
*/
class BTree {
private:
BTreeNode* root; // 根节点指针
int minDegree; // 最小度数 t
public:
/**
* 构造函数
* @param degree 最小度数 t(必须 >= 2)
*/
explicit BTree(int degree) : root(nullptr), minDegree(degree) {
if (degree < 2) {
throw std::invalid_argument("最小度数必须 >= 2");
}
}
/**
* 析构函数
*/
~BTree() {
delete root;
}
/**
* 搜索键值
* @param key 要搜索的键值
* @return 如果找到返回 true
*/
bool search(int key) const {
return root ? root->search(key) : false;
}
/**
* 插入键值
* @param key 要插入的键值
*/
void insert(int key) {
if (root == nullptr) {
// 创建根节点(叶子节点)
root = new BTreeNode(minDegree, true);
root->keys.push_back(key);
} else {
// 如果根节点已满,需要分裂并创建新根
if (root->keys.size() == 2 * minDegree - 1) {
BTreeNode* newRoot = new BTreeNode(minDegree, false);
newRoot->children.push_back(root);
newRoot->splitChild(0, root);
// 确定新键值应该插入哪个子节点
int i = 0;
if (newRoot->keys[0] < key) {
i++;
}
newRoot->children[i]->insertNonFull(key);
root = newRoot;
} else {
root->insertNonFull(key);
}
}
}
/**
* 中序遍历
* @param visit 访问函数
*/
void traverse(std::function<void(int)> visit) const {
if (root) {
root->traverse(visit);
}
}
/**
* 检查树是否为空
*/
bool empty() const {
return root == nullptr;
}
};
// 使用示例
int main() {
BTree btree(3); // 创建最小度数为3的B-树
// 插入数据
std::vector<int> data = {10, 20, 5, 6, 12, 30, 7, 17, 1, 25, 40, 50};
std::cout << "插入数据: ";
for (int val : data) {
std::cout << val << " ";
btree.insert(val);
}
std::cout << std::endl;
// 中序遍历(输出有序序列)
std::cout << "B-树中序遍历: ";
btree.traverse([](int key) { std::cout << key << " "; });
std::cout << std::endl;
// 搜索测试
std::cout << "\n搜索测试:" << std::endl;
std::cout << "搜索 6: " << (btree.search(6) ? "找到" : "未找到") << std::endl;
std::cout << "搜索 15: " << (btree.search(15) ? "找到" : "未找到") << std::endl;
std::cout << "搜索 30: " << (btree.search(30) ? "找到" : "未找到") << std::endl;
return 0;
}
