堆 | 自在学堆
堆(Heap)是一种特殊的完全二叉树数据结构,它在有序和无序之间找到了一个精妙的平衡点。与完全有序的数组不同,堆只要求父节点与子节点之间满足特定的关系;与完全无序的普通树不同,堆通过这种局部有序性,能够高效地维护元素的优先级关系。
这种“半有序”的特性,使得堆在处理优先级问题时表现出色。在任务调度、事件模拟、图算法中的最短路径计算,以及经典的优先队列实现中,堆都是不可或缺的核心数据结构。
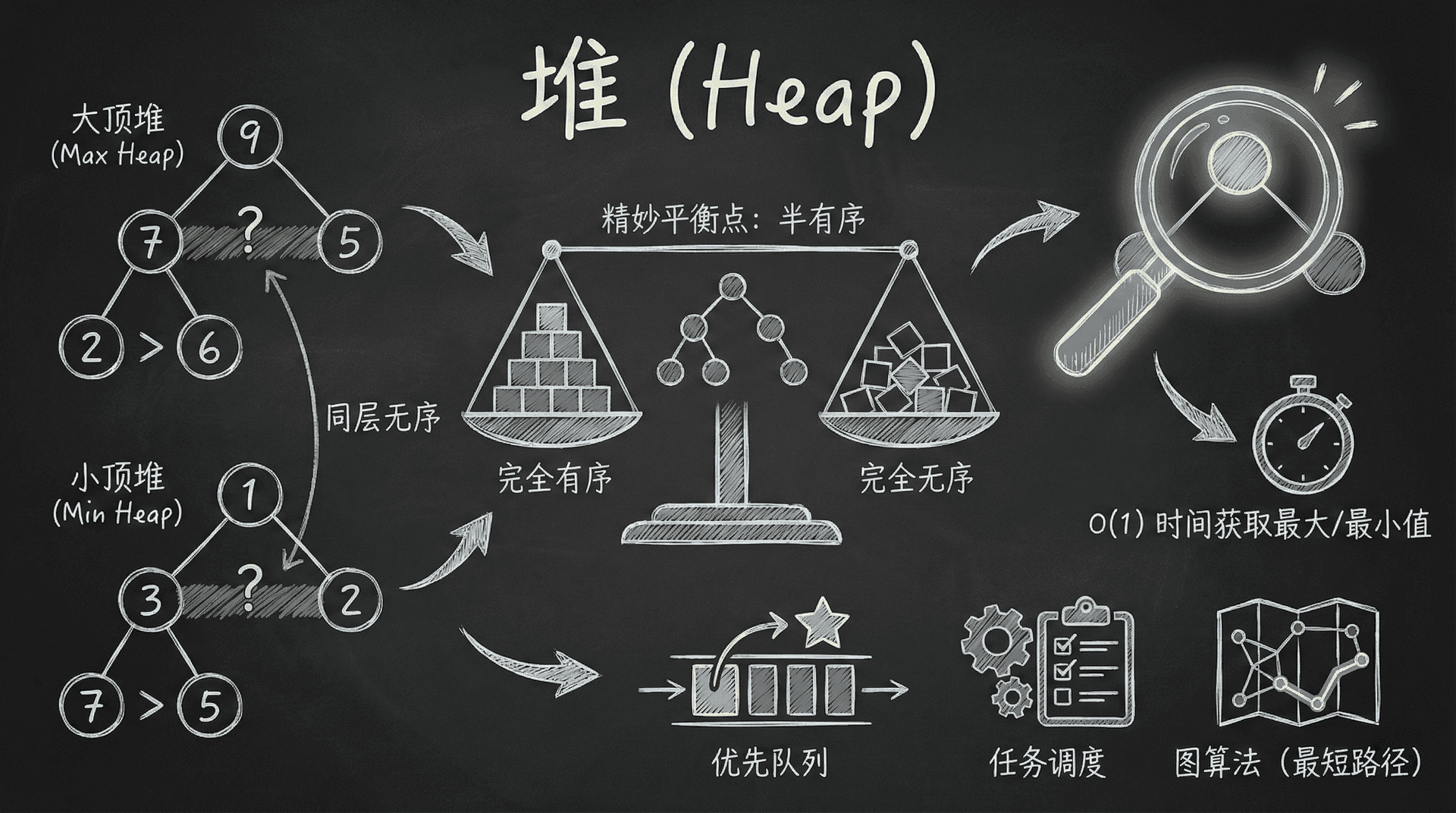
堆的一个关键特性是:通过查看根节点,我们可以在常数时间内找到堆中的最大(或最小)元素。然而,堆并不保证同一层级的节点之间有任何特定的顺序关系,这种设计在保持高效操作的同时,避免了完全排序带来的额外开销。
堆的本质
一个有效的堆结构必须同时满足两个核心条件:
首先,堆在结构上必须是一棵完全二叉树(Complete Binary Tree)。完全二叉树的定义是:除了最后一层外,所有层的节点都是满的;如果最后一层不满,则所有节点必须尽可能靠左排列。这个结构特性保证了堆的紧凑性,避免了树结构中的"空洞",为后续的数组实现奠定了基础。
其次,堆必须满足堆属性(Heap Property)。堆属性规定了父节点与子节点之间的键值关系。根据这种关系的不同,堆可以分为两种类型:
- 最大堆(Max-Heap):对于最大堆中的任意节点,其键值都大于或等于其所有子节点的键值。这意味着根节点存储的是整个堆中的最大值。最大堆适用于需要频繁获取最大元素的场景。
- 最小堆(Min-Heap):对于最小堆中的任意节点,其键值都小于或等于其所有子节点的键值。根节点存储的是整个堆中的最小值。最小堆在需要频繁获取最小元素的场景中非常有用。
在接下来的讨论中,我们主要以最大堆为例来阐述堆的原理和实现。
用数组实现
堆的完全二叉树特性使得我们可以用数组来高效地实现它,而无需使用指针来维护节点之间的连接关系。这种实现方式不仅节省了内存空间,还因为数据的连续存储特性,提高了缓存局部性,从而提升了访问效率。
我们可以按照层次遍历的顺序,将堆中的节点依次存储在数组中。具体来说,从根节点开始,按照从上到下、从左到右的顺序,将每个节点的值存入数组的连续位置。
当堆以数组形式存储后,我们可以通过简单的数学公式,在常数时间内计算出任意节点的父节点和子节点的索引位置,而无需遍历树结构:
- 父节点索引:对于索引为
i 的节点,其父节点的索引为 ⌊(i - 1) / 2⌋,在整数除法下等价于 (i - 1) / 2
- 左子节点索引:
2 * i + 1
- 右子节点索引:
2 * i + 2
例如,对于索引为 2 的节点(键值为80),其父节点索引为 (2-1)/2 = 0(根节点),左子节点索引为 2*2+1 = 5。这种基于索引的计算方式,使得堆的所有操作都能在数组上高效实现。
下面是用C++实现的最大堆类:
#include <iostream>
#include <vector>
#include <stdexcept>
#include <algorithm> // for std::swap
// 最大堆的模板类实现
template <typename T>
class MaxHeap {
private:
// 使用vector存储堆的元素
std::vector<T> heap;
// 获取父节点索引
int getParentIndex(int index) {
return (index - 1) / 2;
}
// 获取左子节点索引
int getLeftChildIndex(int index) {
return 2 * index + 1;
}
// 获取右子节点索引
int getRightChildIndex(int index) {
return 2 * index + 2;
}
public:
// 接下来我们将实现堆的各种操作
};
堆的操作
插入操作与上浮调整 (heapifyUp)
向堆中插入新元素时,我们首先将新元素添加到数组的末尾,即完全二叉树的最后一个位置。这个新元素可能会违反堆属性:如果它的键值大于其父节点的键值(在最大堆中),那么堆属性就被破坏了。
为了恢复堆属性,我们需要执行上浮(heapifyUp 或 siftUp) 操作。上浮过程将新插入的元素与其父节点进行比较,如果新元素更大,则交换它们的位置。这个过程递归地向上进行,直到新元素到达一个满足堆属性的位置,或者成为新的根节点。
// 在 MaxHeap 类中添加
public:
// 上浮调整:从指定索引开始向上调整堆
void heapifyUp(int index) {
// 当节点不是根节点,且其值大于父节点时,继续上浮
while (index > 0 && heap[index] > heap[getParentIndex(index)]) {
// 交换当前节点与父节点
std::swap(heap[index], heap[getParentIndex(index)]);
// 更新索引,继续向上检查
index = getParentIndex(index);
}
}
// 插入新元素
由于堆是完全二叉树,其高度为 O(logn),其中 n 是堆中元素的数量。上浮操作最多需要从叶子节点遍历到根节点,因此插入操作的时间复杂度为 O(logn)。
提取最大值与下沉调整 (heapifyDown)
堆的一个核心操作是提取最大值(在最大堆中)或最小值(在最小堆中)。对于最大堆,最大值总是位于根节点,我们可以直接访问它。但提取后,我们需要维护堆的结构和属性。
一个直观的方法是遍历所有子节点来找到新的最大值,但这种方法的时间复杂度为 O(n),效率不高。堆采用了一种更高效的策略:将数组末尾的元素移动到根节点位置,然后执行**下沉(heapifyDown 或 siftDown)**操作来恢复堆属性。
下沉过程将当前节点与其子节点进行比较,如果子节点中存在更大的值(在最大堆中),则与最大的子节点交换位置。这个过程递归地向下进行,直到当前节点到达一个满足堆属性的位置,或者成为叶子节点。
// 在 MaxHeap 类中添加
public:
// 下沉调整:从指定索引开始向下调整堆
void heapifyDown(int index) {
int largestIndex = index; // 假设当前节点是最大值
int leftChild = getLeftChildIndex(index);
int rightChild = getRightChildIndex(index);
int heapSize = heap.size();
// 比较左子节点与当前最大值
if (leftChild < heapSize && heap[leftChild]
与上浮操作类似,下沉操作最多需要从根节点遍历到叶子节点,因此时间复杂度同样为 O(logn)。
堆的构建
给定一个无序的数组,我们需要将其转换为一个满足堆属性的堆结构。一个直接的方法是创建一个空堆,然后依次将数组中的每个元素插入堆中。每次插入的时间复杂度为 O(logk),其中 k 是当前堆的大小,因此总时间复杂度为 O(nlogn)。
然而,存在一种更高效的自底向上建堆方法,其时间复杂度为 O(n)。这种方法基于一个重要的观察:堆中所有的叶子节点(没有子节点的节点)天然地满足堆属性,因为它们没有子节点需要比较。
因此,我们只需要从最后一个非叶子节点开始,自底向上地对每个节点执行下沉操作。最后一个非叶子节点的索引为 ⌊n/2⌋ - 1,其中 n 是数组的长度。
// 在 MaxHeap 类中添加构造函数,用于从数组构建堆
public:
// 从现有数组构建堆
MaxHeap(const std::vector<T>& array) {
heap = array; // 复制数组
// 从最后一个非叶子节点开始,自底向上执行下沉操作
for (int i = (heap.size() / 2) - 1; i >= 0; --i) {
heapifyDown(i);
}
为什么这种建堆方法的时间复杂度是 O(n) 而不是 O(nlogn)?虽然我们调用了 n/2 次 heapifyDown,但大部分调用都发生在堆的底层,这些节点只需要下沉很少的层数,操作成本很低。只有顶层的少数节点需要下沉较多的层数。通过摊还分析(Amortized Analysis),可以严格证明这个建堆过程的总时间复杂度是线性的。
堆排序与优先队列
堆排序
堆排序(Heapsort)是一种基于堆数据结构的比较排序算法。它利用堆能够高效获取最大(或最小)元素的特性,实现了一个时间复杂度为 O(nlogn) 的原地排序算法。
堆排序分为两个主要阶段:
-
建堆阶段:将无序数组转换为最大堆(或最小堆)。使用自底向上建堆方法,时间复杂度为 O(n)。
-
排序阶段:重复执行以下操作 n−1 次:
a. 交换根节点(当前最大值)与数组末尾的元素。此时,最大值已经位于其最终排序位置。
b. 将堆的有效大小减一(不再考虑已排序的部分)。
c. 对新的根节点执行下沉操作,恢复堆属性。
// 堆排序的独立实现
void heapSort(std::vector<int>& arr) {
int n = arr.size();
// --- 阶段一:建堆 (原地构建最大堆) ---
// 从最后一个非叶子节点开始,对每个节点执行下沉
for (int i = n / 2 - 1; i >= 0; --i) {
// 对 arr[i] 及其子树执行下沉操作
// (需要实现一个接受数组和范围的heapifyDown版本)
堆排序的总时间复杂度为建堆的 O(n) 加上排序阶段的 O(nlogn),因此整体时间复杂度为 O(nlogn)。堆排序与快速排序、归并排序一样,是最高效的通用排序算法之一。此外,堆排序是原地排序算法,空间复杂度为 O(1),这是它的一个重要优势。
优先队列
优先队列(Priority Queue)是一种抽象数据类型,它支持两种主要操作:插入元素和提取优先级最高(或最低)的元素。与普通队列的"先进先出"(FIFO)原则不同,优先队列遵循"优先级优先"的原则。
堆是实现优先队列的理想数据结构。最大堆可以用于实现最大优先队列,最小堆可以用于实现最小优先队列。优先队列在计算机科学中有广泛的应用,包括:
- 任务调度:操作系统中的进程调度器使用优先队列来管理不同优先级的任务。
- 图算法:Dijkstra最短路径算法和Prim最小生成树算法都依赖优先队列。
- 事件驱动模拟:按照事件发生的时间顺序处理事件。
- 数据流处理:从大量数据流中实时获取最值。
使用最大堆实现优先队列的核心操作:
小练习
4. 堆的构建过程练习
给定数组 [3, 10, 1, 8, 5, 12]。
要求:
- 将这个数组逐个插入到一个空的最小堆后,写出最终的数组表示
- 对这个数组使用线性时间建堆法(从最后一个非叶子节点开始执行
heapifyDown)构建一个最大堆后,写出最终的数组表示
#include <iostream>
#include <vector>
#include <sstream>
using namespace std;
// 辅助函数:打印整数向量
string vectorToString(const vector<int>& vec)
{
if (vec.empty()) return "[]";
stringstream ss;
ss << "[";
for (size_t
5. 堆的概念辨析练习
请回答以下问题:
- 在一个最大堆中,最小的元素可能出现在什么位置?请举例说明。
- 为什么说堆排序是一种不稳定的排序算法?
#include <iostream>
using namespace std;
int main()
{
cout << "=== 问题1:最大堆中最小元素的位置 ===" << endl;
cout << "在最大堆中,最小的元素可能出现在任意位置,包括叶子节点。" << endl;
cout << "堆只保证父节点大于子节点,不保证兄弟节点之间的大小关系。" << endl;
cout << endl;
cout << "示例:" << endl;
cout << " 10" << endl;
6. 完善 MaxHeap 类练习
完善 MaxHeap 类,添加以下功能,并分析它们的时间复杂度:
Peek(): 查看根节点的值(最大值),但不删除它IsEmpty(): 检查堆是否为空GetSize(): 获取堆中元素的数量
#include <iostream>
#include <vector>
#include <sstream>
#include <stdexcept>
using namespace std;
// 辅助函数:打印整数向量
string vectorToString(const vector<int>& vec)
{
if (vec.empty()) return "[]";
stringstream ss;
ss << "[";
for
7. 堆的实际应用:任务调度系统练习
假设你正在设计一个任务调度系统。每个任务都有一个优先级(数字越大,优先级越高)。请描述如何使用 MaxHeap 类来管理这些任务,使得每次都能取出优先级最高的任务来执行。
要求:
- 当一个新任务被创建时,应该调用哪个方法?
- 当系统需要执行下一个任务时,应该调用哪个方法?
- 实现一个简单的任务调度系统示例
#include <iostream>
#include <vector>
#include <string>
#include <functional>
#include <stdexcept>
using namespace std;
// 任务类
class Task
{
public:
string name;
int priority;
Task(const string& name, int priority) : name(name), priority(priority)
void insert(const T& value) {
// 将新元素添加到数组末尾
heap.push_back(value);
// 对新插入的元素执行上浮操作,恢复堆属性
heapifyUp(heap.size() - 1);
}
>
heap[largestIndex]) {
largestIndex = leftChild;
}
// 比较右子节点与当前最大值
if (rightChild < heapSize && heap[rightChild] > heap[largestIndex]) {
largestIndex = rightChild;
}
// 如果最大值不是当前节点,需要交换并继续下沉
if (index != largestIndex) {
std::swap(heap[index], heap[largestIndex]);
// 递归地对交换后的位置继续执行下沉操作
heapifyDown(largestIndex);
}
}
// 提取并删除最大值
T extractMax() {
// 检查堆是否为空
if (heap.empty()) {
throw std::out_of_range("堆为空,无法提取最大值");
}
// 保存根节点的值(最大值)
T maxValue = heap[0];
// 将最后一个元素移动到根节点
heap[0] = heap.back();
// 删除最后一个元素
heap.pop_back();
// 对根节点执行下沉操作,恢复堆属性
heapifyDown(0);
// 返回最大值
return maxValue;
}
}
}
// --- 阶段二:排序 ---
for (int i = n - 1; i > 0; --i) {
// 将当前最大值(根节点)交换到其最终位置
std::swap(arr[0], arr[i]);
// 对新的根节点在缩小后的堆上执行下沉操作
// (堆的有效大小为 i)
}
}
i
=
0
; i
<
vec.
size
(); i
++
)
{
ss << vec[i];
if (i < vec.size() - 1) ss << ", ";
}
ss << "]";
return ss.str();
}
class MinHeap
{
private:
vector<int> heap;
public:
MinHeap()
{
// vector 会自动初始化
}
// 插入元素
void insert(int value)
{
heap.push_back(value);
heapifyUp(heap.size() - 1);
}
// 向上调整
void heapifyUp(int index)
{
while (index > 0)
{
int parent = (index - 1) / 2;
if (heap[index] >= heap[parent])
break;
// 交换
swap(heap[index], heap[parent]);
index = parent;
}
}
void printHeap()
{
cout << "堆数组: " << vectorToString(heap) << endl;
}
};
class MaxHeap
{
private:
vector<int> heap;
public:
MaxHeap(const vector<int>& arr)
{
heap = arr;
buildHeap();
}
// 线性时间建堆
void buildHeap()
{
// 从最后一个非叶子节点开始,向上执行 heapifyDown
for (int i = (heap.size() - 2) / 2; i >= 0; i--)
{
heapifyDown(i);
}
}
// 向下调整
void heapifyDown(int index)
{
while (true)
{
int largest = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
if (left < static_cast<int>(heap.size()) && heap[left] > heap[largest])
largest = left;
if (right < static_cast<int>(heap.size()) && heap[right] > heap[largest])
largest = right;
if (largest == index)
break;
// 交换
swap(heap[index], heap[largest]);
index = largest;
}
}
void printHeap()
{
cout << "堆数组: " << vectorToString(heap) << endl;
}
};
int main()
{
vector<int> arr = { 3, 10, 1, 8, 5, 12 };
cout << "原始数组: " << vectorToString(arr) << endl;
cout << endl;
// 1. 逐个插入最小堆
cout << "=== 逐个插入最小堆 ===" << endl;
MinHeap minHeap;
for (int num : arr)
{
minHeap.insert(num);
cout << "插入 " << num << " 后:" << endl;
minHeap.printHeap();
}
// 2. 线性时间建最大堆
cout << "\n=== 线性时间建最大堆 ===" << endl;
MaxHeap maxHeap(arr);
cout << "最终最大堆:" << endl;
maxHeap.printHeap();
return 0;
}
- 逐个插入最小堆:
- 线性时间建最大堆:
- 两种方法的比较:
- 逐个插入:简单直观,但时间复杂度高 O(n log n)
- 线性建堆:效率高 O(n),适合已知所有元素的情况
cout << " / \\" << endl;
cout << " 8 9" << endl;
cout << " / \\ / \\" << endl;
cout << " 7 1 6 5" << endl;
cout << endl;
cout << "这是一个最大堆,最小元素 1 出现在叶子节点。" << endl;
cout << "堆的性质:" << endl;
cout << " - 父节点 >= 子节点(最大堆)" << endl;
cout << " - 但不保证兄弟节点之间的大小关系" << endl;
cout << " - 因此最小元素可能在任意位置" << endl;
cout << endl;
cout << "=== 问题2:堆排序的不稳定性 ===" << endl;
cout << "堆排序是不稳定的排序算法,原因如下:" << endl;
cout << endl;
cout << "1. 堆调整过程中的交换:" << endl;
cout << " 在 heapifyDown 过程中,可能会交换相同值的元素" << endl;
cout << " 例如:两个值为 5 的元素,在堆调整后可能改变相对位置" << endl;
cout << endl;
cout << "2. 具体例子:" << endl;
cout << " 原始数组: [5a, 3, 5b, 1]" << endl;
cout << " 构建最大堆后: [5a, 3, 5b, 1]" << endl;
cout << " 排序过程中,5a 和 5b 的相对位置可能改变" << endl;
cout << " 排序后: [1, 3, 5b, 5a] 或 [1, 3, 5a, 5b]" << endl;
cout << endl;
cout << "3. 不稳定的定义:" << endl;
cout << " 如果排序算法能够保持相同值元素的相对位置,则称为稳定" << endl;
cout << " 堆排序无法保证这一点,因此是不稳定的" << endl;
return 0;
}
=== 问题1:最大堆中最小元素的位置 ===
在最大堆中,最小的元素可能出现在任意位置,包括叶子节点。
堆只保证父节点大于子节点,不保证兄弟节点之间的大小关系。
示例:
10
/ \
8 9
/ \ / \
7 1 6 5
这是一个最大堆,最小元素 1 出现在叶子节点。
堆的性质:
- 父节点 >= 子节点(最大堆)
- 但不保证兄弟节点之间的大小关系
- 因此最小元素可能在任意位置
=== 问题2:堆排序的不稳定性 ===
堆排序是不稳定的排序算法,原因如下:
1. 堆调整过程中的交换:
在 heapifyDown 过程中,可能会交换相同值的元素
例如:两个值为 5 的元素,在堆调整后可能改变相对位置
2. 具体例子:
原始数组: [5a, 3, 5b, 1]
构建最大堆后: [5a, 3, 5b, 1]
排序过程中,5a 和 5b 的相对位置可能改变
排序后: [1, 3, 5b, 5a] 或 [1, 3, 5a, 5b]
3. 不稳定的定义:
如果排序算法能够保持相同值元素的相对位置,则称为稳定
堆排序无法保证这一点,因此是不稳定的
- 最大堆中最小元素的位置:
- 可能出现在任意位置,包括叶子节点
- 堆只保证父节点大于子节点,不保证兄弟节点之间的大小关系
- 示例中最小元素 1 出现在叶子节点
- 堆排序的不稳定性:
- 在堆调整过程中,可能会交换相同值的元素
- 相同值的元素在排序后可能改变相对位置
- 因此堆排序是不稳定的排序算法
(
size_t
i
=
0
; i
<
vec.
size
(); i
++
)
{
ss << vec[i];
if (i < vec.size() - 1) ss << ", ";
}
ss << "]";
return ss.str();
}
class MaxHeap
{
private:
vector<int> heap;
public:
MaxHeap()
{
// vector 会自动初始化
}
// 插入元素 - O(log n)
void insert(int value)
{
heap.push_back(value);
heapifyUp(heap.size() - 1);
}
// 向上调整
void heapifyUp(int index)
{
while (index > 0)
{
int parent = (index - 1) / 2;
if (heap[index] <= heap[parent])
break;
swap(heap[index], heap[parent]);
index = parent;
}
}
// 查看根节点的值(最大值),但不删除 - O(1)
int peek()
{
if (heap.empty())
throw runtime_error("堆为空");
return heap[0];
}
// 检查堆是否为空 - O(1)
bool isEmpty()
{
return heap.empty();
}
// 获取堆中元素的数量 - O(1)
int getSize()
{
return heap.size();
}
// 删除并返回最大值 - O(log n)
int extractMax()
{
if (heap.empty())
throw runtime_error("堆为空");
int max = heap[0];
heap[0] = heap[heap.size() - 1];
heap.pop_back();
if (!heap.empty())
{
heapifyDown(0);
}
return max;
}
// 向下调整
void heapifyDown(int index)
{
while (true)
{
int largest = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
if (left < static_cast<int>(heap.size()) && heap[left] > heap[largest])
largest = left;
if (right < static_cast<int>(heap.size()) && heap[right] > heap[largest])
largest = right;
if (largest == index)
break;
swap(heap[index], heap[largest]);
index = largest;
}
}
void printHeap()
{
cout << "堆数组: " << vectorToString(heap) << endl;
}
};
int main()
{
MaxHeap heap;
cout << "创建最大堆并插入元素:" << endl;
heap.insert(10);
heap.insert(5);
heap.insert(15);
heap.insert(8);
heap.insert(20);
heap.printHeap();
cout << "\n堆的大小: " << heap.getSize() << endl;
cout << "堆是否为空: " << (heap.isEmpty() ? "true" : "false") << endl;
cout << "堆顶元素(最大值): " << heap.peek() << endl;
cout << "\n删除最大值:" << endl;
int max = heap.extractMax();
cout << "删除的元素: " << max << endl;
heap.printHeap();
cout << "删除后堆的大小: " << heap.getSize() << endl;
cout << "\n时间复杂度分析:" << endl;
cout << " - Peek(): O(1) - 直接访问根节点" << endl;
cout << " - IsEmpty(): O(1) - 检查列表大小" << endl;
cout << " - GetSize(): O(1) - 返回列表大小" << endl;
cout << " - Insert(): O(log n) - 需要向上调整" << endl;
cout << " - ExtractMax(): O(log n) - 需要向下调整" << endl;
return 0;
}
创建最大堆并插入元素:
堆数组: [20, 15, 10, 5, 8]
堆的大小: 5
堆是否为空: False
堆顶元素(最大值): 20
删除最大值:
删除的元素: 20
堆数组: [15, 8, 10, 5]
删除后堆的大小: 4
时间复杂度分析:
- Peek(): O(1) - 直接访问根节点
- IsEmpty(): O(1) - 检查列表大小
- GetSize(): O(1) - 返回列表大小
- Insert(): O(log n) - 需要向上调整
- ExtractMax(): O(log n) - 需要向下调整
- Peek():时间复杂度 O(1),直接访问根节点(索引0)
- IsEmpty():时间复杂度 O(1),检查列表大小是否为0
- GetSize():时间复杂度 O(1),返回列表的大小
- 关键点:
- 这三个方法都是 O(1) 操作,因为只需要访问或检查列表的大小
- 不需要调整堆的结构
- 实现简单高效
{
}
string toString() const
{
return name + " (优先级: " + to_string(priority) + ")";
}
};
// 通用最大堆(使用函数对象)
template<typename T>
class MaxHeap
{
private:
vector<T> heap;
function<bool(const T&, const T&)> compare; // 返回 true 表示第一个元素优先级更高
public:
MaxHeap(function<bool(const T&, const T&)> comp) : compare(comp)
{
// vector 会自动初始化
}
void insert(const T& item)
{
heap.push_back(item);
heapifyUp(heap.size() - 1);
}
T extractMax()
{
if (heap.empty())
throw runtime_error("堆为空");
T max = heap[0];
heap[0] = heap[heap.size() - 1];
heap.pop_back();
if (!heap.empty())
heapifyDown(0);
return max;
}
T peek()
{
if (heap.empty())
throw runtime_error("堆为空");
return heap[0];
}
bool isEmpty()
{
return heap.empty();
}
private:
void heapifyUp(int index)
{
while (index > 0)
{
int parent = (index - 1) / 2;
if (!compare(heap[index], heap[parent]))
break;
swap(heap[index], heap[parent]);
index = parent;
}
}
void heapifyDown(int index)
{
while (true)
{
int largest = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
if (left < static_cast<int>(heap.size()) && compare(heap[left], heap[largest]))
largest = left;
if (right < static_cast<int>(heap.size()) && compare(heap[right], heap[largest]))
largest = right;
if (largest == index)
break;
swap(heap[index], heap[largest]);
index = largest;
}
}
};
// 任务调度系统
class TaskScheduler
{
private:
MaxHeap<Task> taskHeap;
public:
TaskScheduler() : taskHeap([](const Task& a, const Task& b) {
return a.priority > b.priority; // 优先级高的在前
})
{
}
// 添加新任务 - O(log n)
void addTask(const Task& task)
{
taskHeap.insert(task);
cout << "添加任务: " << task.toString() << endl;
}
// 执行下一个任务(优先级最高的) - O(log n)
bool executeNextTask()
{
if (taskHeap.isEmpty())
{
cout << "没有待执行的任务" << endl;
return false;
}
Task task = taskHeap.extractMax();
cout << "执行任务: " << task.toString() << endl;
return true;
}
// 查看下一个要执行的任务(不删除) - O(1)
bool peekNextTask(string& taskName)
{
if (taskHeap.isEmpty())
return false;
Task task = taskHeap.peek();
taskName = task.toString();
return true;
}
bool hasTasks()
{
return !taskHeap.isEmpty();
}
};
int main()
{
TaskScheduler scheduler;
cout << "=== 任务调度系统 ===" << endl << endl;
// 添加任务
cout << "1. 添加新任务:" << endl;
scheduler.addTask(Task("任务A", 5));
scheduler.addTask(Task("任务B", 10));
scheduler.addTask(Task("任务C", 3));
scheduler.addTask(Task("任务D", 8));
scheduler.addTask(Task("任务E", 12));
cout << "\n2. 查看下一个要执行的任务:" << endl;
string nextTask;
if (scheduler.peekNextTask(nextTask))
{
cout << "下一个任务: " << nextTask << endl;
}
cout << "\n3. 执行任务(按优先级从高到低):" << endl;
while (scheduler.hasTasks())
{
scheduler.executeNextTask();
}
cout << "\n总结:" << endl;
cout << " - 新任务创建时: 调用 addTask() 方法(内部调用 insert())" << endl;
cout << " - 执行下一个任务时: 调用 executeNextTask() 方法(内部调用 extractMax())" << endl;
cout << " - 时间复杂度: 添加和执行都是 O(log n)" << endl;
cout << " - 优势: 总是能快速获取优先级最高的任务" << endl;
return 0;
}
=== 任务调度系统 ===
1. 添加新任务:
添加任务: 任务A (优先级: 5)
添加任务: 任务B (优先级: 10)
添加任务: 任务C (优先级: 3)
添加任务: 任务D (优先级: 8)
添加任务: 任务E (优先级: 12)
2. 查看下一个要执行的任务:
下一个任务: 任务E (优先级: 12)
3. 执行任务(按优先级从高到低):
执行任务: 任务E (优先级: 12)
执行任务: 任务B (优先级: 10)
执行任务: 任务D (优先级: 8)
执行任务: 任务A (优先级: 5)
执行任务: 任务C (优先级: 3)
总结:
- 新任务创建时: 调用 AddTask() 方法(内部调用 Insert())
- 执行下一个任务时: 调用 ExecuteNextTask() 方法(内部调用 ExtractMax())
- 时间复杂度: 添加和执行都是 O(log n)
- 优势: 总是能快速获取优先级最高的任务
- 新任务创建时:调用
AddTask() 方法(内部调用 Insert())
- 时间复杂度:O(log n)
- 将任务插入堆中,自动维护堆的性质
- 执行下一个任务时:调用
ExecuteNextTask() 方法(内部调用 ExtractMax())
- 时间复杂度:O(log n)
- 取出优先级最高的任务(堆顶),并调整堆
- 优势:
- 总是能快速获取优先级最高的任务
- 插入和执行操作都是 O(log n),效率高
- 适合动态任务调度场景
