图 | 自在学
图
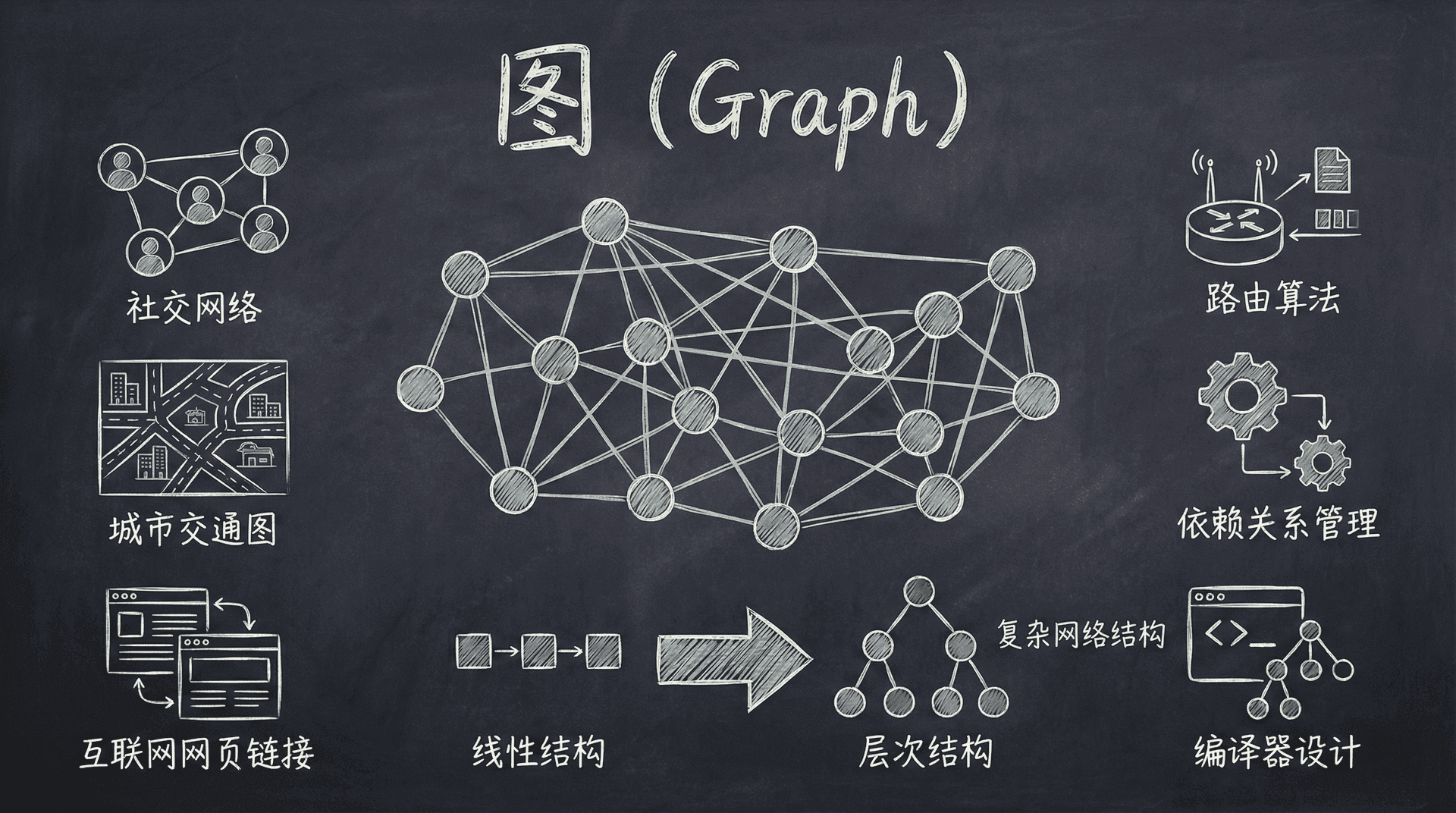
在数据结构的学习中,我们已经掌握了数组、链表等线性结构,以及树这样的层次结构。然而,许多实际问题中的关系无法用简单的线性或层次关系表示,需要更复杂的网络结构来描述实体之间的多对多关系。
图(Graph) 是一种重要的非线性数据结构,用于表示具有复杂关系的数据集合。图结构在计算机科学中应用广泛,包括社交网络分析、路由算法、依赖关系管理、编译器设计等领域。
从社交网络中的用户关系、城市交通图中的道路连接,到互联网中的网页链接,图无处不在,它能够精确地模拟现实世界中任何复杂的多对多关系。
图的定义与基本概念
形式化定义
设 G = ( V , E ) G = (V, E) G = ( V , E ) V V V E ⊆ V × V E \subseteq V \times V E ⊆ V × V ( u , v ) (u, v) ( u , v ) u u u v v v ( u , v ) (u, v) ( u , v ) u u u v v v
图 G = ( V , E ) G = (V, E) G = ( V , E )
顶点(Vertex) ,也称为节点(Node) ,是图中的基本实体,用 v ∈ V v \in V v ∈ V 边(Edge) ,也称为弧(Arc) ,是连接两个顶点的关系,用 e = ( u , v ) ∈ E e = (u, v) \in E e = ( u , v ) ∈ E ( u , v ) (u, v) ( u , v )
图的分类
根据边的性质和权重的存在性,图可以分为不同的类型,每种类型适用于不同的应用场景。
无向图(Undirected Graph) :图中的边是无序的,即边 ( u , v ) (u, v) ( u , v ) ( v , u ) (v, u) ( v , u ) ( u , v ) (u, v) ( u , v ) u u u v v v 相邻(Adjacent) 的,边
理解了图的这些基本分类,我们就能开始思考如何在计算机程序中高效地表示和操作这些复杂的网络结构。
图的表示方法
要在程序中表示一张图,我们主要有两种经典的方法:邻接矩阵(Adjacency Matrix)和 邻接表(Adjacency List) 。选择哪一种表示方法,取决于图的密度(边的数量相对于顶点的数量)、需要频繁执行的操作类型,以及可用的存储空间。
邻接矩阵
邻接矩阵(Adjacency Matrix) 是一种直观的图表示方法。对于包含 ∣ V ∣ |V| ∣ V ∣ G = ( V , E ) G = (V, E) G = ( V , E ) ∣ V ∣ × ∣ V ∣ |V| \times |V| ∣ V ∣ × ∣ V ∣ A A A
对于无权图,如果存在边 ( i , j ) (i, j) ( i , j ) A [ i ] [ j ] = 1 A[i][j] = 1 A [ i ] [ j ] = 1 A [ i ] [ j ] = 0 A[i][j] = 0 A [ i ] [ j ] = 0 A [ i ] [ j
对于加权图,A [ i ] [ j ] A[i][j] A [ i ] [ j ] ( i , j ) (i, j) ( i , j ) ∞ \infty ∞ − 1 -1 − 1
空间复杂度 :邻接矩阵的空间复杂度为 O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ 2 ) n n n n 2 n^2 n 2
时间复杂度分析 :
查询操作 :判断顶点 i i i j j j O ( 1 ) O(1) O ( 1 ) A [ i ] [ j ] A[i][j] A [ i ] [ j ] 遍历邻接顶点 :获取顶点 i i i i i i
优点 :
查询效率高 :判断两个顶点之间是否存在边的操作时间复杂度为 O ( 1 ) O(1) O ( 1 ) 实现简单 :使用二维数组即可实现,代码结构清晰,易于理解和维护。适合稠密图 :对于边数接近 ∣ V ∣ 2 |V|^2 ∣ V ∣ 2 缺点 :
空间复杂度高 :空间复杂度为 O ( ∣ V ∣ 2 ) O(|V|^2) O ( ∣ V ∣ #include <iostream> #include <vector>
// 使用邻接矩阵表示一个简单的无向无权图 class GraphMatrix { private: // adjMatrix 是一个二维向量,用来存储邻接矩阵 std ::vector < std ::vector <int>> adjMatrix; // numVertices 存储顶点的数量 int numVertices;
public: // 构造函数,初始化一个有 V 个顶点的图 GraphMatrix ( int V ) { numVertices = V; // 将二维向量的大小调整为 V x V,并用0填充 adjMatrix. resize (V, 邻接表
邻接表(Adjacency List) 是针对邻接矩阵空间浪费问题的有效解决方案。邻接表为每个顶点维护一个列表,该列表只存储与该顶点相邻的顶点,而不是存储所有可能的顶点对。
具体来说,我们创建一个大小为 ∣ V ∣ |V| ∣ V ∣ i i i i i i i i i
空间复杂度 :邻接表的空间复杂度为 O ( ∣ V ∣ + ∣ E ∣ ) O(|V| + |E|) O ( ∣ V ∣ + ∣ E ∣ ) n n n m m m n n n m m m ∣ E ∣ ≪ ∣
时间复杂度分析 :
查询操作 :判断顶点 i i i j j j i i i O ( deg ( i ) ) O(\text{deg}(i)) O ( deg ( i )) deg ( i ) \text{deg}(i) deg ( i ) i i i
优点 :
空间高效 :空间复杂度为 O ( ∣ V ∣ + ∣ E ∣ ) O(|V| + |E|) O ( ∣ V ∣ + ∣ E ∣ ) 遍历邻接顶点效率高 :获取顶点 i i i O ( deg ( i ) ) O(\text{deg}(i)) O ( deg ( i )) 适合稀疏图 :对于边数远小于 ∣ V ∣ 2 |V|^2 在实际应用中,大多数图都是稀疏图(边的数量远小于 ∣ V ∣ 2 |V|^2 ∣ V ∣ 2 邻接表是实际应用中最常用、最高效的图表示方法 。大多数图算法库和数据结构实现都采用邻接表作为默认的图表示方法。
#include <iostream> #include <vector> #include <list>
// 使用邻接表表示一个简单的无向无权图 class GraphList { private: // adjList 是一个向量,每个元素是一个存储整数的链表 // 数组的索引代表顶点,链表中的元素代表该顶点的邻接顶点 std ::vector < std ::list <int>> adjList; // numVertices 存储顶点的数量 int numVertices;
public: // 构造函数,初始化一个有 V 个顶点的图 GraphList ( int V ) { numVertices = V; // 将向量的大小调整为 V,每个位置都是一个空的链表 图的遍历算法
图的遍历是指系统性地访问图中的每一个顶点,确保每个顶点被访问且仅被访问一次的过程。遍历算法是图算法的基础,许多复杂的图算法都建立在遍历算法之上。
最经典、最重要的两种遍历策略是广度优先搜索(BFS)和 深度优先搜索(DFS) 。这两种算法采用不同的访问策略,适用于不同的应用场景。
广度优先搜索 (BFS)
**广度优先搜索(Breadth-First Search, BFS)**采用层次遍历的策略,从起始顶点开始,先访问距离起始顶点最近的顶点(第一层),然后访问距离起始顶点次近的顶点(第二层),以此类推,逐层向外扩展。
为了实现这种层次访问顺序,BFS 使用**队列(Queue)**这种先进先出(FIFO)的数据结构来维护待访问的顶点序列。
算法描述 :
设图 G = ( V , E ) G = (V, E) G = ( V , E ) s ∈ V s \in V s ∈ V
BFS(G, s): 初始化 visited 数组,标记所有顶点为未访问 创建队列 Q visited[s] = true Q.enqueue(s) while Q 不为空: u = Q.dequeue() 访问顶点 u for each 顶点 v in adjList[u]: // 遍历 u 的所有邻接顶点 if visited[v] == false: visited[v] = true Q.enqueue(v) 算法正确性 :BFS 算法能够访问从起始顶点 s s s k k k s s s k k k
时间复杂度分析 :对于包含 ∣ V ∣ |V| ∣ V ∣ ∣ E ∣ |E| ∣ E ∣ O ( ∣ V ∣ + ∣ E ∣ ) O(|V| + |E|) O ( ∣ V ∣ + ∣ E ∣ )
空间复杂度分析 :BFS 的空间复杂度为 O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) visited 数组需要 O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ )
重要应用 :BFS 的一个重要应用是在无权图中寻找最短路径 。由于 BFS 按照距离起始顶点的远近逐层访问,它找到的从起始顶点到目标顶点的第一条路径,必然是经过边数最少的最短路径。这个性质使得 BFS 成为解决无权图最短路径问题的标准算法。
#include <iostream> #include <vector> #include <list> #include <queue>
class Graph { private: int numVertices; std ::vector < std ::list <int>> adjList;
public: Graph ( int V ) : numVertices (V) { adjList. resize (V); }
void addEdge ( int 深度优先搜索 (DFS)
深度优先搜索(Depth-First Search, DFS) 采用深度优先的策略,从起始顶点开始,选择一条路径尽可能深地探索,直到无法继续前进(到达没有未访问邻接顶点的顶点),然后回溯到上一个顶点,选择另一条路径继续探索。
DFS 可以使用递归 实现,也可以使用显式栈 实现。递归实现简洁直观,直接反映了 DFS 的递归性质;显式栈实现避免了递归调用的函数调用开销,在某些情况下性能更好。
算法描述 :
设图 G = ( V , E ) G = (V, E) G = ( V , E ) s ∈ V s \in V s ∈ V
DFS(G, s): 初始化 visited 数组,标记所有顶点为未访问 DFS_Visit(G, s, visited)
DFS_Visit(G, u, visited): visited[u] = true 访问顶点 u for each 顶点 v in adjList[u]: // 遍历 u 的所有邻接顶点 if visited[v] == false: DFS_Visit(G, v, visited) // 递归访问未访问的邻接顶点 算法正确性 :DFS 算法能够访问从起始顶点 s s s s s s v v v v v v
时间复杂度分析 :对于包含 ∣ V ∣ |V| ∣ V ∣ ∣ E ∣ |E| ∣ E ∣ O ( ∣ V ∣ + ∣ E ∣ ) O(|V| + |E|) O ( ∣ V ∣ + ∣ E ∣ )
空间复杂度分析 :DFS 的空间复杂度取决于实现方式。对于递归实现,空间复杂度为 O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) ∣ V ∣ |V| ∣ V ∣ O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ )
重要应用 :DFS 在图算法中应用广泛,包括检测图中是否存在环路 、进行拓扑排序 (确定有向无环图中顶点的线性顺序)、寻找连通分量 (找出图中所有相互连通的顶点集合)、强连通分量分解 (找出有向图中所有强连通的子图)等。
#include <iostream> #include <vector> #include <list>
class GraphDFS { private: int numVertices; std ::vector < std ::list <int>> adjList;
// DFS 的辅助递归函数 // 时间复杂度: O(|V| + |E|),空间复杂度: O(|V|) void DFSUtil ( int u , std :: vector < bool > & visited ) { // 标记当前顶点为已访问并访问它 小练习
A. O(n²)
B. O(n + m)
C. O(n)
D. O(m)
A. O(n²)
B. O(n + m)
C. O(n)
D. O(m)
A. DFS
B. BFS
C. 两者都可以
D. 两者都不可以
4. 图的表示方法复杂度分析练习
设图 G = (V, E) 包含 n 个顶点和 m 条边。请分析以下问题:
使用邻接矩阵表示图 G 时,空间复杂度是多少?如果 m << n²(稀疏图),这种表示方法的主要缺点是什么?
使用邻接表表示图 G 时,空间复杂度是多少?对于稀疏图,为什么邻接表比邻接矩阵更高效?
在无权图中,为什么 BFS 能够找到从起始顶点到目标顶点的最短路径?
#include <iostream> using namespace std ;
int main () { cout << "=== 图的表示方法复杂度分析 ===" << endl << endl;
cout << "1. 邻接矩阵:" << endl; cout << " - 空间复杂度: O(n²)" << endl; cout << " - 原因: 使用 n×n 的二维数组存储所有可能的边" << endl; cout << " - 稀疏图的缺点:" << endl; cout 5. 图的遍历模拟练习
给定以下有向图,顶点编号为 0 到 5(A=0, B=1, C=2, D=3, E=4, F=5):
A -> B, A -> C
B -> D, B -> E
C -> E
D -> F
E -> F
要求:
手动模拟从顶点 0(A)开始的 BFS 遍历,写出访问顶点的顺序
手动模拟从顶点 0(A)开始的 DFS 遍历,写出访问顶点的顺序
#include <iostream> #include <vector> #include <queue> #include <sstream> using namespace std ;
// 辅助函数:打印整数向量 string vectorToString ( const vector < int > & vec ) { if (vec. empty ()) return "[]" ; stringstream ss; ss << "[" ; for 6. 检测有向图中的环路练习
实现一个 HasCycle() 方法,用于检测一个有向图中是否存在环路。
要求:使用 DFS 实现,在 DFS 遍历时,除了 visited 数组,还需要一个 recursionStack 数组来跟踪当前递归路径上的顶点。如果访问到一个已经在当前递归路径中的顶点,则说明存在环路。
#include <iostream> #include <vector> using namespace std ;
class Graph { private: int vertices; vector < vector <int>> adjList;
public: Graph ( int v ) : vertices (v) { adjList. resize (v); }
void addEdge ( int ( v , u ) (v, u) ( v , u )
度(Degree)是描述顶点连接数量的重要概念。对于无向图,顶点 v v v deg ( v ) \text{deg}(v) deg ( v ) v v v v v v 入度(In-degree) deg − ( v ) \text{deg}^-(v) deg − ( v ) v v v 出度(Out-degree) deg + ( v ) \text{deg}^+(v) deg + ( v ) v v v ( u , v )
关联(Incident)
有向图(Directed Graph) :图中的边是有序的,边 ( u , v ) (u, v) ( u , v ) u u u v v v ( v , u ) (v, u) ( v , u ) ( u , v ) (u, v) ( u , v ) u u u v v v 前驱(Predecessor) ,v v v u u u 后继(Successor) 。加权图(Weighted Graph) :图中的每条边都被赋予一个数值,称为权重(Weight) 。权重可以表示距离、成本、时间、容量等不同的度量。对于加权图,边可以表示为三元组 ( u , v , w ) (u, v, w) ( u , v , w ) w w w
无权图(Unweighted Graph) :图中的所有边都没有权重,或者可以认为所有边的权重都相等。无权图适用于只关心连接关系存在性而不关心关系强度的场景。A [ i ] [ j ] A[i][j] A [ i ] [ j ]
] = 1 A[i][j] = 1 A [ i ] [ j ] = 1
A [ i ] [ j ] = A [ j ] [ i ] A[i][j] = A[j][i] A [ i ] [ j ] = A [ j ] [ i ] i
添加或删除边 :对于无权图,添加或删除边的时间复杂度为 O ( 1 ) O(1) O ( 1 ) O ( 1 ) O(1) O ( 1 ) 2
)
遍历邻接顶点效率低 :获取顶点 i i i i i i O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) ∣ V ∣ |V| ∣ V ∣ 不适合稀疏图 :对于边数远小于 ∣ V ∣ 2 |V|^2 ∣ V ∣ 2 0 0 0 std
::
vector
<
int
>(V,
0
));
}
// 添加一条从顶点 u 到顶点 v 的边
void addEdge ( int u , int v ) {
// 检查顶点是否在有效范围内
if (u >= 0 && u < numVertices && v >= 0 && v < numVertices) {
// 在邻接矩阵中标记边的存在
adjMatrix[u][v] = 1 ;
// 因为是无向图,所以两个方向都要标记
adjMatrix[v][u] = 1 ;
}
}
// 查询顶点 u 和 v 之间是否存在边,时间复杂度 O(1)
bool hasEdge ( int u , int v ) {
if (u >= 0 && u < numVertices && v >= 0 && v < numVertices) {
return adjMatrix[u][v] == 1 ;
}
return false ;
}
// 打印邻接矩阵,方便我们观察图的结构
void printGraph () {
std ::cout << "Adjacency Matrix:" << std ::endl;
for ( int i = 0 ; i < numVertices; ++ i) {
for ( int j = 0 ; j < numVertices; ++ j) {
// 打印矩阵的每个元素,并在后面加一个空格
std ::cout << adjMatrix[i][j] << " " ;
}
// 每打印完一行后换行
std ::cout << std ::endl;
}
}
};
int main_matrix () {
// 创建一个有4个顶点的图
GraphMatrix g ( 4 );
// 添加边,连接各个顶点
g. addEdge ( 0 , 1 ); // 添加边 (0, 1)
g. addEdge ( 0 , 2 ); // 添加边 (0, 2)
g. addEdge ( 1 , 2 ); // 添加边 (1, 2)
g. addEdge ( 2 , 3 ); // 添加边 (2, 3)
// 打印图的邻接矩阵表示
g. printGraph ();
return 0 ;
}
V ∣ 2 |E| \ll |V|^2 ∣ E ∣ ≪ ∣ V ∣ 2
i
遍历邻接顶点 :获取顶点 i i i i i i O ( deg ( i ) ) O(\text{deg}(i)) O ( deg ( i )) 添加边 :在顶点 i i i j j j O ( 1 ) O(1) O ( 1 ) O ( 1 ) O(1) O ( 1 ) 删除边 :从顶点 i i i j j j O ( deg ( i ) ) O(\text{deg}(i)) O ( deg ( i )) ∣ V ∣ 2
查询效率较低 :判断两个顶点之间是否存在边,需要遍历其中一个顶点的邻接表,时间复杂度为 O ( deg ( i ) ) O(\text{deg}(i)) O ( deg ( i )) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) 实现相对复杂 :需要使用动态数据结构(链表或向量),代码实现比邻接矩阵稍复杂。 adjList. resize (V);
}
// 添加一条从顶点 u 到顶点 v 的边,时间复杂度 O(1)
void addEdge ( int u , int v ) {
// 检查顶点是否在有效范围内
if (u >= 0 && u < numVertices && v >= 0 && v < numVertices) {
// 在 u 的邻接表中添加 v
adjList[u]. push_back (v);
// 因为是无向图,所以也要在 v 的邻接表中添加 u
adjList[v]. push_back (u);
}
}
// 查询顶点 u 和 v 之间是否存在边,时间复杂度 O(deg(u))
bool hasEdge ( int u , int v ) {
if (u >= 0 && u < numVertices && v >= 0 && v < numVertices) {
// 遍历顶点 u 的邻接表,查找顶点 v
for ( int neighbor : adjList[u]) {
if (neighbor == v) {
return true ;
}
}
}
return false ;
}
// 打印邻接表,方便我们观察图的结构
void printGraph () {
std ::cout << "Adjacency List:" << std ::endl;
for ( int i = 0 ; i < numVertices; ++ i) {
// 打印当前顶点
std ::cout << "Vertex " << i << ":" ;
// 遍历该顶点的邻接表
for ( int neighbor : adjList[i]) {
// 打印每个邻接顶点
std ::cout << " -> " << neighbor;
}
// 打印完一个顶点的所有邻接顶点后换行
std ::cout << std ::endl;
}
}
};
int main_list () {
// 创建一个有4个顶点的图
GraphList g ( 4 );
// 添加边,连接各个顶点
g. addEdge ( 0 , 1 );
g. addEdge ( 0 , 2 );
g. addEdge ( 1 , 2 );
g. addEdge ( 2 , 3 );
// 打印图的邻接表表示
g. printGraph ();
return 0 ;
}
u
,
int
v
) {
adjList[u]. push_back (v);
// adjList[v].push_back(u); // 如果是无向图,取消注释
}
// 从指定的 startVertex 开始执行广度优先搜索
// 时间复杂度: O(|V| + |E|),空间复杂度: O(|V|)
void BFS ( int startVertex ) {
// visited 数组用于跟踪哪些顶点已经被访问过
std ::vector <bool> visited (numVertices, false );
// 创建一个队列用于 BFS
std ::queue <int> q;
// 将起始顶点标记为已访问并将其入队
visited[startVertex] = true ;
q. push (startVertex);
std ::cout << "BFS starting from vertex " << startVertex << ": " ;
// 当队列不为空时,循环继续
while ( ! q. empty ()) {
// 从队列中取出一个顶点并访问它
int u = q. front ();
q. pop ();
std ::cout << u << " " ;
// 遍历当前顶点的所有邻接顶点
for ( int v : adjList[u]) {
// 如果邻接顶点尚未被访问
if ( ! visited[v]) {
// 将其标记为已访问并入队
visited[v] = true ;
q. push (v);
}
}
}
std ::cout << std ::endl;
}
};
int main_bfs () {
// 创建一个有向图
Graph g ( 6 );
g. addEdge ( 0 , 1 );
g. addEdge ( 0 , 2 );
g. addEdge ( 1 , 3 );
g. addEdge ( 1 , 4 );
g. addEdge ( 2 , 4 );
g. addEdge ( 3 , 5 );
g. addEdge ( 4 , 5 );
g. BFS ( 0 ); // 从顶点0开始BFS
return 0 ;
}
visited[u] = true ;
std ::cout << u << " " ;
// 遍历当前顶点的所有邻接顶点
for ( int v : adjList[u]) {
// 如果邻接顶点尚未被访问,则递归地对它进行DFS
if ( ! visited[v]) {
DFSUtil (v, visited);
}
}
}
public:
GraphDFS ( int V ) : numVertices (V) {
adjList. resize (V);
}
void addEdge ( int u , int v ) {
adjList[u]. push_back (v);
}
// 从指定的 startVertex 开始执行深度优先搜索
// 时间复杂度: O(|V| + |E|),空间复杂度: O(|V|)
void DFS ( int startVertex ) {
// visited 数组用于跟踪哪些顶点已经被访问过
std ::vector <bool> visited (numVertices, false );
std ::cout << "DFS starting from vertex " << startVertex << ": " ;
// 调用辅助函数开始递归
DFSUtil (startVertex, visited);
std ::cout << std ::endl;
}
};
int main_dfs () {
GraphDFS g ( 6 );
g. addEdge ( 0 , 1 );
g. addEdge ( 0 , 2 );
g. addEdge ( 1 , 3 );
g. addEdge ( 1 , 4 );
g. addEdge ( 2 , 4 );
g. addEdge ( 3 , 5 );
g. addEdge ( 4 , 5 );
g. DFS ( 0 ); // 从顶点0开始DFS
return 0 ;
}
<<
" * 浪费大量空间存储不存在的边"
<<
endl;
cout << " * 例如:n=1000, m=1000 时,需要 1,000,000 个存储单元" << endl;
cout << " * 但实际只需要存储 1000 条边" << endl;
cout << endl;
cout << "2. 邻接表:" << endl;
cout << " - 空间复杂度: O(n + m)" << endl;
cout << " - 原因: 使用数组存储顶点,每个顶点对应一个链表存储邻接边" << endl;
cout << " - 稀疏图的优势:" << endl;
cout << " * 只存储实际存在的边" << endl;
cout << " * 空间利用率高,适合稀疏图" << endl;
cout << " * 例如:n=1000, m=1000 时,只需要约 2000 个存储单元" << endl;
cout << endl;
cout << "3. BFS 找最短路径:" << endl;
cout << " - BFS 按层遍历,先访问的顶点距离更近" << endl;
cout << " - 在无权图中,边的权重都是1" << endl;
cout << " - BFS 保证第一次访问某个顶点时,路径最短" << endl;
cout << " - 例如:从 A 到 F 的最短路径,BFS 会先找到" << endl;
cout << endl;
cout << "比较总结:" << endl;
cout << " - 邻接矩阵: 适合稠密图,查询边是否存在 O(1)" << endl;
cout << " - 邻接表: 适合稀疏图,空间效率高" << endl;
cout << " - 选择依据: 根据图的密度(m 与 n² 的关系)选择" << endl;
return 0 ;
}
=== 图的表示方法复杂度分析 ===
1. 邻接矩阵: - 空间复杂度: O(n²) - 原因: 使用 n×n 的二维数组存储所有可能的边 - 稀疏图的缺点: * 浪费大量空间存储不存在的边 * 例如:n=1000, m=1000 时,需要 1,000,000 个存储单元 * 但实际只需要存储 1000 条边
2. 邻接表: - 空间复杂度: O(n + m) - 原因: 使用数组存储顶点,每个顶点对应一个链表存储邻接边 - 稀疏图的优势: * 只存储实际存在的边 * 空间利用率高,适合稀疏图 * 例如:n=1000, m=1000 时,只需要约 2000 个存储单元
3. BFS 找最短路径: - BFS 按层遍历,先访问的顶点距离更近 - 在无权图中,边的权重都是1 - BFS 保证第一次访问某个顶点时,路径最短 - 例如:从 A 到 F 的最短路径,BFS 会先找到
比较总结: - 邻接矩阵: 适合稠密图,查询边是否存在 O(1) - 邻接表: 适合稀疏图,空间效率高 - 选择依据: 根据图的密度(m 与 n² 的关系)选择
邻接矩阵 :
空间复杂度:O(n²)
优点:查询边是否存在 O(1)
缺点:对于稀疏图浪费空间
邻接表 :
空间复杂度:O(n + m)
优点:只存储实际存在的边,空间效率高
缺点:查询边是否存在需要 O(度)
BFS 找最短路径 :
BFS 按层遍历,保证第一次访问某个顶点时路径最短
在无权图中,BFS 能找到最短路径
时间复杂度:O(n + m)
(
size_t
i
=
0
; i
<
vec.
size
(); i
++
)
{
ss << vec[i];
if (i < vec. size () - 1 ) ss << ", " ;
}
ss << "]" ;
return ss. str ();
}
// 辅助函数:打印队列(通过复制)
string queueToString ( queue < int > q )
{
if (q. empty ()) return "[]" ;
stringstream ss;
ss << "[" ;
bool first = true ;
while ( ! q. empty ())
{
if ( ! first) ss << ", " ;
ss << q. front ();
q. pop ();
first = false ;
}
ss << "]" ;
return ss. str ();
}
class Graph
{
private:
int vertices;
vector < vector <int>> adjList;
public:
Graph ( int v ) : vertices (v)
{
adjList. resize (v);
}
void addEdge ( int u , int v )
{
adjList[u]. push_back (v);
}
// BFS 遍历
void bfs ( int start )
{
vector <bool> visited (vertices, false );
queue <int> que;
vector <int> result;
visited[start] = true ;
que. push (start);
cout << "BFS 从顶点 " << start << " 开始:" << endl;
cout << "初始状态: 队列=[" << start << "], 访问顺序=[]" << endl;
int step = 1 ;
while ( ! que. empty ())
{
int current = que. front ();
que. pop ();
result. push_back (current);
cout << " \n 步骤 " << step << ": 出队顶点 " << current << endl;
cout << " 访问顺序: " << vectorToString (result) << endl;
for ( int neighbor : adjList[current])
{
if ( ! visited[neighbor])
{
visited[neighbor] = true ;
que. push (neighbor);
cout << " 入队顶点 " << neighbor << endl;
}
}
cout << " 队列状态: " << queueToString (que) << endl;
step ++ ;
}
cout << " \n BFS 遍历完成,访问顺序: " << vectorToString (result) << endl;
}
// DFS 遍历
void dfs ( int start )
{
vector <bool> visited (vertices, false );
vector <int> result;
int step = 1 ;
cout << " \n DFS 从顶点 " << start << " 开始:" << endl;
dfsHelper (start, visited, result, step);
cout << " \n DFS 遍历完成,访问顺序: " << vectorToString (result) << endl;
}
private:
void dfsHelper ( int v , vector < bool > & visited , vector < int > & result , int& step )
{
visited[v] = true ;
result. push_back (v);
cout << "步骤 " << step << ": 访问顶点 " << v
<< ", 访问顺序: " << vectorToString (result) << endl;
step ++ ;
for ( int neighbor : adjList[v])
{
if ( ! visited[neighbor])
{
cout << " 递归访问顶点 " << neighbor << endl;
dfsHelper (neighbor, visited, result, step);
}
}
}
};
int main ()
{
// 顶点映射: A=0, B=1, C=2, D=3, E=4, F=5
Graph g ( 6 );
g. addEdge ( 0 , 1 ); // A -> B
g. addEdge ( 0 , 2 ); // A -> C
g. addEdge ( 1 , 3 ); // B -> D
g. addEdge ( 1 , 4 ); // B -> E
g. addEdge ( 2 , 4 ); // C -> E
g. addEdge ( 3 , 5 ); // D -> F
g. addEdge ( 4 , 5 ); // E -> F
cout << "有向图结构:" << endl;
cout << " A -> B, A -> C" << endl;
cout << " B -> D, B -> E" << endl;
cout << " C -> E" << endl;
cout << " D -> F" << endl;
cout << " E -> F" << endl;
cout << endl;
g. bfs ( 0 );
g. dfs ( 0 );
return 0 ;
}
有向图结构: A -> B, A -> C B -> D, B -> E C -> E D -> F E -> F
BFS 从顶点 0 开始: 初始状态: 队列=[0], 访问顺序=[]
步骤 1: 出队顶点 0 访问顺序: [0] 入队顶点 1 入队顶点 2 队列状态: [1, 2]
步骤 2: 出队顶点 1 访问顺序: [0, 1] 入队顶点 3 入队顶点 4 队列状态: [2, 3, 4]
步骤 3: 出队顶点 2 访问顺序: [0, 1, 2] 队列状态: [3, 4]
步骤 4: 出队顶点 3 访问顺序: [0, 1, 2, 3] 入队顶点 5 队列状态: [4, 5]
步骤 5: 出队顶点 4 访问顺序: [0, 1, 2, 3, 4] 队列状态: [5]
步骤 6: 出队顶点 5 访问顺序: [0, 1, 2, 3, 4, 5]
BFS 遍历完成,访问顺序: [0, 1, 2, 3, 4, 5]
DFS 从顶点 0 开始: 步骤 1: 访问顶点 0, 访问顺序: [0] 递归访问顶点 1 步骤 2: 访问顶点 1, 访问顺序: [0, 1] 递归访问顶点 3 步骤 3: 访问顶点 3, 访问顺序: [0, 1, 3] 递归访问顶点 5 步骤 4: 访问顶点 5, 访问顺序: [0, 1, 3, 5] 递归访问顶点 4 步骤 5: 访问顶点 4, 访问顺序: [0, 1, 3, 5, 4] 递归访问顶点 2 步骤 6: 访问顶点 2, 访问顺序: [0, 1, 3, 5, 4, 2]
DFS 遍历完成,访问顺序: [0, 1, 3, 5, 4, 2]
BFS 遍历顺序 :0, 1, 2, 3, 4, 5(A, B, C, D, E, F)
按层遍历,先访问距离起点近的顶点
使用队列实现,保证先入队的先访问
DFS 遍历顺序 :0, 1, 3, 5, 4, 2(A, B, D, F, E, C)
深度优先,尽可能深入再回溯
使用递归实现,递归调用栈模拟遍历过程
关键区别 :
BFS:按层遍历,适合找最短路径
DFS:深度优先,适合遍历所有路径
u
,
int
v
)
{
adjList[u]. push_back (v);
}
// 检测有向图中是否存在环路
bool hasCycle ()
{
vector <bool> visited (vertices, false );
vector <bool> recursionStack (vertices, false );
// 对每个未访问的顶点进行DFS
for ( int i = 0 ; i < vertices; i ++ )
{
if ( ! visited[i])
{
if ( hasCycleHelper (i, visited, recursionStack))
{
return true ;
}
}
}
return false ;
}
private:
bool hasCycleHelper ( int v , vector < bool > & visited , vector < bool > & recursionStack )
{
// 标记当前顶点为已访问
visited[v] = true ;
// 将当前顶点加入递归栈(当前路径)
recursionStack[v] = true ;
// 遍历所有邻接顶点
for ( int neighbor : adjList[v])
{
// 如果邻接顶点未被访问,递归检查
if ( ! visited[neighbor])
{
if ( hasCycleHelper (neighbor, visited, recursionStack))
{
return true ;
}
}
// 如果邻接顶点在当前递归路径中,说明存在环路
else if (recursionStack[neighbor])
{
return true ;
}
}
// 回溯:将当前顶点从递归栈中移除
recursionStack[v] = false ;
return false ;
}
};
int main ()
{
// 测试1:无环图
cout << "测试1:无环图" << endl;
Graph g1 ( 4 );
g1. addEdge ( 0 , 1 );
g1. addEdge ( 0 , 2 );
g1. addEdge ( 1 , 3 );
cout << "是否存在环路: " << (g1. hasCycle () ? "true" : "false" ) << endl; // false
// 测试2:有环图
cout << " \n 测试2:有环图" << endl;
Graph g2 ( 4 );
g2. addEdge ( 0 , 1 );
g2. addEdge ( 1 , 2 );
g2. addEdge ( 2 , 0 ); // 形成环路 0 -> 1 -> 2 -> 0
g2. addEdge ( 2 , 3 );
cout << "是否存在环路: " << (g2. hasCycle () ? "true" : "false" ) << endl; // true
// 测试3:自环
cout << " \n 测试3:自环" << endl;
Graph g3 ( 3 );
g3. addEdge ( 0 , 1 );
g3. addEdge ( 1 , 1 ); // 自环
cout << "是否存在环路: " << (g3. hasCycle () ? "true" : "false" ) << endl; // true
cout << " \n 复杂度分析:" << endl;
cout << " - 时间复杂度: O(V + E)" << endl;
cout << " 原因: 需要遍历所有顶点和边" << endl;
cout << " - 空间复杂度: O(V)" << endl;
cout << " 原因: visited 和 recursionStack 数组各需要 O(V) 空间" << endl;
cout << " 递归调用栈在最坏情况下深度为 O(V)" << endl;
return 0 ;
}
测试1:无环图 是否存在环路: False
测试2:有环图 是否存在环路: True
测试3:自环 是否存在环路: True
复杂度分析: - 时间复杂度: O(V + E) 原因: 需要遍历所有顶点和边 - 空间复杂度: O(V) 原因: visited 和 recursionStack 数组各需要 O(V) 空间 递归调用栈在最坏情况下深度为 O(V)
算法思路 :
使用 DFS 遍历图
visited 数组标记已访问的顶点recursionStack 数组跟踪当前递归路径上的顶点如果访问到一个已经在 recursionStack 中的顶点,说明存在环路
关键点 :
回溯时需要将顶点从 recursionStack 中移除
只有当前递归路径中的顶点才算环路,已访问但不在当前路径中的不算
时间复杂度 :O(V + E),需要遍历所有顶点和边空间复杂度 :O(V),需要 visited 和 recursionStack 数组,递归调用栈深度为 O(V)与遍历算法的比较 :
时间复杂度相同:O(V + E)
空间复杂度相同:O(V)
但需要额外的 recursionStack 数组来跟踪当前路径