树 | 自在学
树
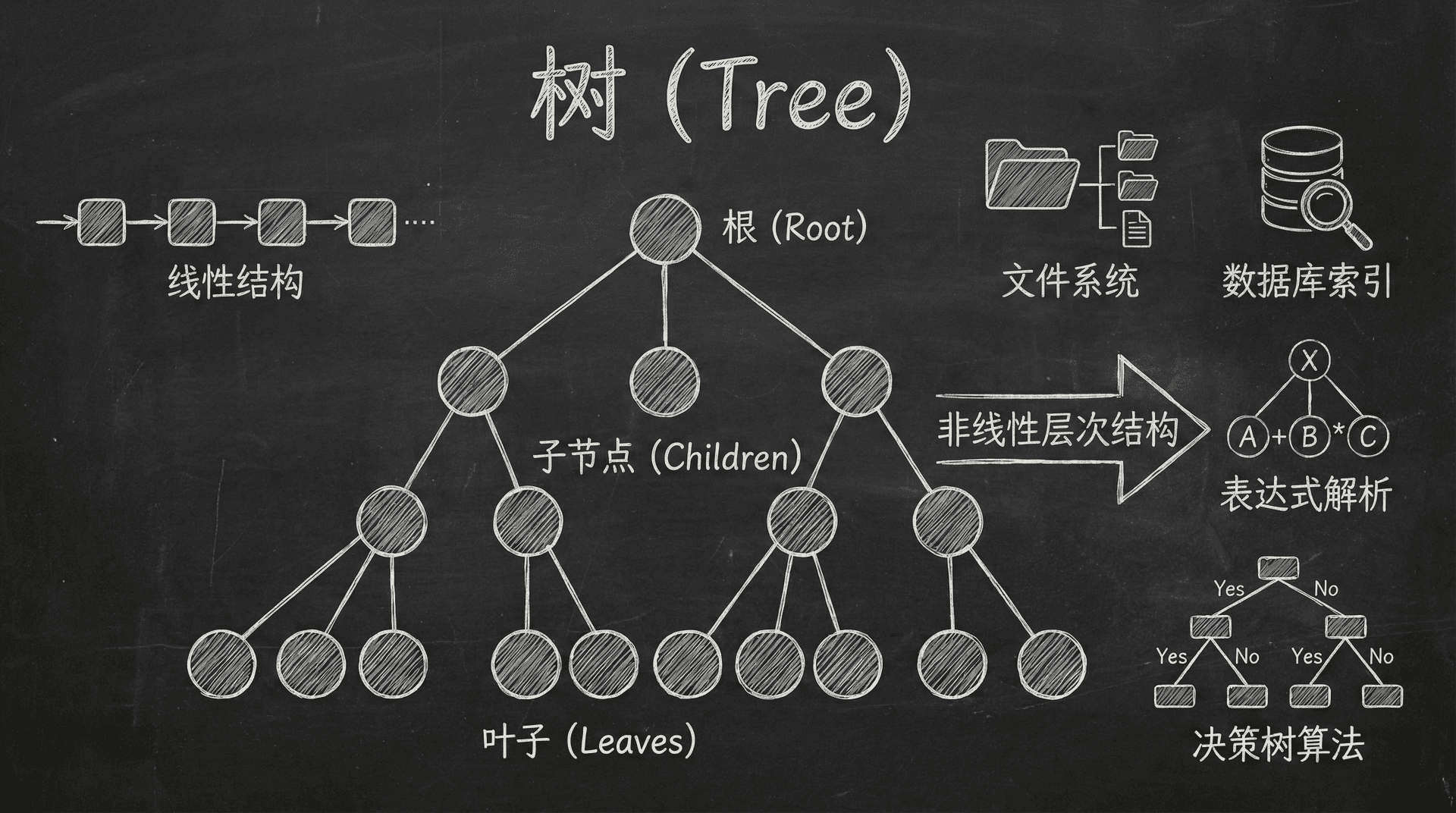
在数据结构的学习中,我们已经掌握了数组、链表、栈和队列等线性数据结构。这些结构中的元素按照线性顺序排列,每个元素(除首尾外)都有唯一的前驱和后继。然而,许多实际问题中的关系无法用简单的线性关系表示,需要更复杂的层次化结构。
树(Tree) 是一种重要的非线性数据结构,用于表示具有层次关系的数据集合。树结构在计算机科学中应用广泛,包括文件系统、数据库索引、表达式解析、决策树算法等领域。
树的定义与基本概念
形式化定义
设 T = ( V , E ) T = (V, E) T = ( V , E ) V V V E ⊆ V × V E \subseteq V \times V E ⊆ V × V T T T T T T
连通性 :对于任意两个节点 u , v ∈ V u, v \in V u , v ∈ V u u u v v v 无环性 :T T T 根节点存在性 :存在唯一的节点 r ∈ V r \in V r ∈ V
在树 T = ( V , E ) T = (V, E) T = ( V , E ) ( u , v ) ∈ E (u, v) \in E ( u , v ) ∈ E u u u v v v 父节点(Parent) ,v v
基本术语
对于树 T = ( V , E ) T = (V, E) T = ( V , E )
根节点(Root) :入度为 0 的唯一节点,记为 r r r 叶子节点(Leaf) :出度为 0 的节点集合,即 L = { v ∈ V : deg + ( v ) = 0 } L = \{v \in V : \text{deg}^+(v) = 0\} L = { v ∈ V : deg + ( v ) = 0 } 内部节点(Internal Node) :非叶子节点的集合,即 V ∖ L
路径与距离
路径(Path) :从节点 u u u v v v P = ( v 0 , v 1 , … , v k ) P = (v_0, v_1, \ldots, v_k) P = ( v 0 , v 1 ,
深度(Depth) :节点 v v v depth ( v ) \text{depth}(v) depth ( v ) r r r v v v depth ( r ) = 0 \text{depth}(r) = 0 depth ( r ) = 0
高度(Height) :树 T T T height ( T ) \text{height}(T) height ( T ) ‘ height ( T ) = max v ∈ V depth ( v ) ‘ `\text{height}(T) = \max_{v \in V} \text{depth}(v)` ‘ height ( T ) = max v ∈ V depth
子树(Subtree) :对于节点 v ∈ V v \in V v ∈ V v v v T v = ( V v , E v ) T_v = (V_v, E_v) T v = ( V v
树的基本性质
定理 1 :对于包含 n n n T = ( V , E ) T = (V, E) T = ( V , E ) ∣ E ∣ = ∣ V ∣ − 1 |E| = |V| - 1 ∣ E ∣ = ∣ V ∣ − 1
证明 :使用数学归纳法。当 n = 1 n = 1 n = 1 n = k n = k n = k n = k + 1 n = k + 1 n = k + 1 k k k k − 1 k - 1
二叉树
定义
二叉树(Binary Tree)是一种特殊的树结构,其中每个节点最多有两个子节点,分别称为 左子节点(Left Child)和 右子节点(Right Child) 。
形式化地,二叉树 T = ( V , E ) T = (V, E) T = ( V , E ) v ∈ V v \in V v ∈ V ∣ children ( v ) ∣ ≤ 2 |\text{children}(v)| \leq 2 ∣ children ( v ) ∣ ≤ 2
二叉树的分类
完美二叉树(Perfect Binary Tree)
定义 :高度为 h h h
所有内部节点都有两个子节点。
所有叶子节点都在第 h h h
性质 :高度为 h h h 2 h + 1 − 1 2^{h+1} - 1 2 h + 1 − 1 i i i 0 ≤ i ≤ h 0 \leq i \leq h 0 ≤ i ≤ h
满二叉树(Full Binary Tree)
定义 :满二叉树满足:对于任意节点 v v v ∣ children ( v ) ∣ = 0 |\text{children}(v)| = 0 ∣ children ( v ) ∣ = 0 ∣ children ( v ) ∣ = 2 |\text{children}(v)| = 2 ∣ children ( v ) ∣ = 2
性质 :满二叉树不要求所有叶子节点在同一层,但要求所有非叶子节点都有两个子节点。
完全二叉树(Complete Binary Tree)
定义 :高度为 h h h
前 h h h h − 1 h-1 h − 1
第 h h h
性质 :完全二叉树适合用数组表示。对于索引为 i i i
左子节点索引:2 i + 1 2i + 1 2 i + 1
右子节点索引:2 i + 2 2i + 2 2 i + 2
父节点索引:⌊ ( i − 1 ) / 2 ⌋ \lfloor (i - 1) / 2 \rfloor ⌊( i − 1 ) /2 ⌋
树的遍历
树的遍历(Tree Traversal)是指按照某种规则访问树中每个节点且仅访问一次的过程。根据访问顺序的不同,遍历算法可分为两大类:深度优先遍历(Depth-First Search, DFS)和 广度优先遍历(Breadth-First Search, BFS) 。
深度优先遍历(DFS)
深度优先遍历采用递归策略,优先访问深层节点。对于二叉树,根据根节点访问时机的不同,DFS 可分为三种标准遍历方式。
前序遍历(Pre-order Traversal)
定义 :对于以节点 v v v
访问根节点 v v v
递归遍历左子树
递归遍历右子树
算法正确性 :使用结构归纳法可证明前序遍历访问每个节点恰好一次。对于空树,算法正确。假设对于高度小于 h h h h h h h h h
应用场景 :
树的序列化:前序遍历序列可用于重建树结构
表达式求值:前缀表达式(波兰表示法)对应表达式树的前序遍历
目录结构复制:需要先创建目录再复制子目录
中序遍历(In-order Traversal)
定义 :对于以节点 v v v
递归遍历左子树
访问根节点 v v v
递归遍历右子树
重要性质 :对于二叉搜索树(BST),中序遍历产生严格递增的有序序列。
应用场景 :
二叉搜索树排序:中序遍历 BST 得到有序序列,时间复杂度 O ( n ) O(n) O ( n )
表达式树:中序遍历对应中缀表达式,需考虑运算符优先级
BST 性质验证:验证树是否为有效的二叉搜索树
后序遍历(Post-order Traversal)
定义 :对于以节点 v v v
递归遍历左子树
递归遍历右子树
访问根节点 v v v
应用场景 :
内存管理:删除树结构时必须采用后序遍历,确保子节点先于父节点释放
目录大小计算:需要先计算子目录大小再计算父目录
表达式求值:后缀表达式(逆波兰表示法)对应表达式树的后序遍历
树高计算:递归计算子树高度的标准方法
广度优先遍历(BFS)
广度优先遍历,也称为层序遍历(Level-order Traversal) ,按照树的层次逐层访问节点。
算法描述 :
初始化队列 Q Q Q
当 Q Q Q
出队节点 v v v
将 v v v
重复步骤 2 直到 Q Q Q
形式化描述 :设 Q Q Q levelorder ( T ) \text{levelorder}(T) levelorder ( T )
Q. enqueue ( root (T)) while not Q. empty (): v = Q. dequeue () visit (v) for each child c of v: Q. enqueue (c) 复杂度分析
时间复杂度 :对于包含 n n n O ( n ) O(n) O ( n )
空间复杂度分析 :
深度优先遍历(递归实现) :
最坏情况:树退化为链状结构,递归深度为 n n n O ( n ) O(n) O ( n )
最好情况:平衡二叉树,高度 h = ⌊ log 2 n ⌋ h = \lfloor \log_2 n \rfloor h = ⌊ log 2 n ⌋ O ( log n ) O(\log n) O (
深度优先遍历(迭代实现) :
广度优先遍历 :
最坏情况:完美二叉树,最后一层包含 ⌈ n / 2 ⌉ \lceil n/2 \rceil ⌈ n /2 ⌉ O ( n ) O(n) O ( n )
最好情况:链状树,队列最大大小为 1,空间复杂度 O ( 1 ) O(1) O ( 1 )
平均情况:对于随机树,空间复杂度 O ( n ) O(n) O ( n )
定理 2 :对于包含 n n n Ω ( n ) \Omega(n) Ω ( n ) O ( n ) O(n) O ( n )
证明 :考虑完美二叉树,最后一层包含 ⌈ n / 2 ⌉ \lceil n/2 \rceil ⌈ n /2 ⌉ Ω ( n ) \Omega(n) Ω ( n ) O ( n ) O(n) O ( n ) □ \square □
遍历可视化
遍历算法的实现
递归实现
递归实现简洁直观,直接反映遍历的数学定义。
#include <iostream> #include <queue> #include <stack> #include <string> #include <vector>
using namespace std ;
// 二叉树节点定义 template < typename T > struct TreeNode { T data; TreeNode * left; TreeNode * right;
TreeNode ( T val ) : data (val), 迭代实现
迭代实现使用显式栈模拟递归调用,避免递归调用的函数调用开销。
// 前序遍历(迭代) template < typename T > void preorderIterative ( TreeNode < T > * root , vector < T > & result ) { if (root == nullptr ) return ; stack < TreeNode < T >*> stk; stk. push (root); 主函数示例
int main () { // 构建示例树: // F // / \ // B G // / \ \ // A D I // / \ / // C E H TreeNode < string >* root = new TreeNode < string >( "F" ); root->left = new TreeNode < string >( "B" ); root->right = 小练习
A. 根 -> 左 -> 右
B. 左 -> 根 -> 右
C. 左 -> 右 -> 根
D. 按层从左到右
A. O(1)
B. O(log n)
C. O(n)
D. O(n²)
A. O(1)
B. O(log n)
C. O(n)
D. O(n²)
4. 二叉树遍历序列推导练习
给定以下二叉树,请写出四种遍历方式的访问序列:
要求:分别写出前序遍历、中序遍历、后序遍历和层序遍历的序列。
#include <iostream> #include <vector> #include <queue> #include <sstream> using namespace std ;
// 二叉树节点 struct TreeNode { char val; TreeNode * left; TreeNode * right;
TreeNode ( char v ) : val (v), left ( nullptr ), right ( 5. 根据遍历序列重建树练习
已知某二叉树的遍历序列如下:
前序遍历 :1, 2, 4, 5, 3, 6, 7中序遍历 :4, 2, 5, 1, 6, 3, 7
要求:
根据前序和中序遍历序列重建二叉树
推导后序遍历序列
推导层序遍历序列
#include <iostream> #include <vector> #include <queue> #include <unordered_map> #include <sstream> using namespace std ;
struct TreeNode { int val; TreeNode * left; TreeNode * right;
TreeNode ( int v ) : val (v), left ( nullptr ), right 6. 二叉树遍历的复杂度分析练习
分析以下三种特殊形状的二叉树在不同遍历方式下的空间复杂度:
情况A :链状树(高度 n-1)情况B :完全二叉树(高度 ⌊log₂n⌋)情况C :满二叉树(高度 ⌊log₂n⌋)
要求:对于每种情况,分别分析DFS(递归实现)、DFS(迭代实现)和BFS的空间复杂度。
#include <iostream> using namespace std ;
int main () { cout << "=== 二叉树遍历的空间复杂度分析 ===" << endl << endl;
cout << "情况A:链状树(高度 n-1)" << endl; cout << " - DFS(递归实现): O(n)" << endl; cout << " 原因:递归调用栈的深度等于树的高度 n-1" << endl; cout << " - DFS(迭代实现): O(n)" << endl; v ∈ V ∖ { r } v \in V \setminus \{r\} v ∈ V ∖ { r }
v
子节点(Child)
根节点(Root)
V \setminus L V ∖ L
兄弟节点(Sibling) :具有相同父节点的节点集合。对于节点 v v v { u ∈ V : parent ( u ) = parent ( v ) , u ≠ v } \{u \in V : \text{parent}(u) = \text{parent}(v), u \neq v\} { u ∈ V : parent ( u ) = parent ( v ) , u = v } 祖先节点(Ancestor) :从根节点到节点 v v v v v v 后代节点(Descendant) :以节点 v v v v v v …
,
v k
)
( v i , v i + 1 ) ∈ E (v_i, v_{i+1}) \in E ( v i , v i + 1 ) ∈ E (
v
)
‘
,
E v
)
k
−
1
( k − 1 ) + 1 = k (k - 1) + 1 = k ( k − 1 ) + 1 = k ∣ E ∣ = ∣ V ∣ − 1 |E| = |V| - 1 ∣ E ∣ = ∣ V ∣ − 1 2 i 2^i 2 i
log
n
)
平均情况:对于随机树,空间复杂度 O ( log n ) O(\log n) O ( log n ) left
(
nullptr
),
right
(
nullptr
) {}
// 析构函数:后序遍历删除子树
~TreeNode () {
if (left) delete left;
if (right) delete right;
}
};
// 前序遍历(递归)
template < typename T >
void preorderRecursive ( TreeNode < T > * root , vector < T > & result ) {
if (root == nullptr ) return ;
result. push_back (root->data); // 访问根节点
preorderRecursive (root->left, result); // 遍历左子树
preorderRecursive (root->right, result); // 遍历右子树
}
// 中序遍历(递归)
template < typename T >
void inorderRecursive ( TreeNode < T > * root , vector < T > & result ) {
if (root == nullptr ) return ;
inorderRecursive (root->left, result); // 遍历左子树
result. push_back (root->data); // 访问根节点
inorderRecursive (root->right, result); // 遍历右子树
}
// 后序遍历(递归)
template < typename T >
void postorderRecursive ( TreeNode < T > * root , vector < T > & result ) {
if (root == nullptr ) return ;
postorderRecursive (root->left, result); // 遍历左子树
postorderRecursive (root->right, result); // 遍历右子树
result. push_back (root->data); // 访问根节点
}
// 层序遍历(使用队列)
template < typename T >
void levelorderTraversal ( TreeNode < T > * root , vector < T > & result ) {
if (root == nullptr ) return ;
queue < TreeNode < T >*> q;
q. push (root);
while ( ! q. empty ()) {
TreeNode < T >* current = q. front ();
q. pop ();
result. push_back (current->data);
if (current->left != nullptr ) {
q. push (current->left);
}
if (current->right != nullptr ) {
q. push (current->right);
}
}
}
while ( ! stk. empty ()) {
TreeNode < T >* node = stk. top ();
stk. pop ();
result. push_back (node->data);
// 注意:先压入右子树,再压入左子树,保证左子树先出栈
if (node->right != nullptr ) {
stk. push (node->right);
}
if (node->left != nullptr ) {
stk. push (node->left);
}
}
}
// 中序遍历(迭代)
template < typename T >
void inorderIterative ( TreeNode < T > * root , vector < T > & result ) {
stack < TreeNode < T >*> stk;
TreeNode < T >* current = root;
while (current != nullptr || ! stk. empty ()) {
// 一直向左走到底
while (current != nullptr ) {
stk. push (current);
current = current->left;
}
// 回溯到父节点
current = stk. top ();
stk. pop ();
result. push_back (current->data);
// 转向右子树
current = current->right;
}
}
// 后序遍历(迭代)
template < typename T >
void postorderIterative ( TreeNode < T > * root , vector < T > & result ) {
if (root == nullptr ) return ;
stack < TreeNode < T >*> stk;
TreeNode < T >* lastVisited = nullptr ;
TreeNode < T >* current = root;
while (current != nullptr || ! stk. empty ()) {
// 一直向左走到底
while (current != nullptr ) {
stk. push (current);
current = current->left;
}
TreeNode < T >* peekNode = stk. top ();
// 如果右子树存在且未被访问,转向右子树
if (peekNode->right != nullptr && peekNode->right != lastVisited) {
current = peekNode->right;
} else {
// 访问当前节点
result. push_back (peekNode->data);
lastVisited = stk. top ();
stk. pop ();
}
}
}
new
TreeNode
<
string
>(
"G"
);
root->left->left = new TreeNode < string >( "A" );
root->left->right = new TreeNode < string >( "D" );
root->left->right->left = new TreeNode < string >( "C" );
root->left->right->right = new TreeNode < string >( "E" );
root->right->right = new TreeNode < string >( "I" );
root->right->right->left = new TreeNode < string >( "H" );
vector < string > result;
cout << "递归实现:" << endl;
preorderRecursive (root, result);
cout << "前序遍历: " ;
for ( const auto& val : result) cout << val << " " ;
cout << endl;
result. clear ();
inorderRecursive (root, result);
cout << "中序遍历: " ;
for ( const auto& val : result) cout << val << " " ;
cout << endl;
result. clear ();
postorderRecursive (root, result);
cout << "后序遍历: " ;
for ( const auto& val : result) cout << val << " " ;
cout << endl;
result. clear ();
levelorderTraversal (root, result);
cout << "层序遍历: " ;
for ( const auto& val : result) cout << val << " " ;
cout << endl;
cout << " \n 迭代实现:" << endl;
result. clear ();
preorderIterative (root, result);
cout << "前序遍历: " ;
for ( const auto& val : result) cout << val << " " ;
cout << endl;
result. clear ();
inorderIterative (root, result);
cout << "中序遍历: " ;
for ( const auto& val : result) cout << val << " " ;
cout << endl;
result. clear ();
postorderIterative (root, result);
cout << "后序遍历: " ;
for ( const auto& val : result) cout << val << " " ;
cout << endl;
// 使用析构函数自动释放内存
delete root;
return 0 ;
}
nullptr
) {}
};
// 辅助函数:打印字符向量
string vectorToString ( const vector < char > & vec )
{
if (vec. empty ()) return "[]" ;
stringstream ss;
ss << "[" ;
for ( size_t i = 0 ; i < vec. size (); i ++ )
{
ss << vec[i];
if (i < vec. size () - 1 ) ss << ", " ;
}
ss << "]" ;
return ss. str ();
}
// 前序遍历:根 -> 左 -> 右
void preOrder ( TreeNode * root , vector < char > & result )
{
if (root == nullptr ) return ;
result. push_back (root->val); // 访问根节点
preOrder (root->left, result); // 遍历左子树
preOrder (root->right, result); // 遍历右子树
}
// 中序遍历:左 -> 根 -> 右
void inOrder ( TreeNode * root , vector < char > & result )
{
if (root == nullptr ) return ;
inOrder (root->left, result); // 遍历左子树
result. push_back (root->val); // 访问根节点
inOrder (root->right, result); // 遍历右子树
}
// 后序遍历:左 -> 右 -> 根
void postOrder ( TreeNode * root , vector < char > & result )
{
if (root == nullptr ) return ;
postOrder (root->left, result); // 遍历左子树
postOrder (root->right, result); // 遍历右子树
result. push_back (root->val); // 访问根节点
}
// 层序遍历:按层从左到右
void levelOrder ( TreeNode * root , vector < char > & result )
{
if (root == nullptr ) return ;
queue < TreeNode *> que;
que. push (root);
while ( ! que. empty ())
{
TreeNode * node = que. front ();
que. pop ();
result. push_back (node->val);
if (node->left != nullptr )
que. push (node->left);
if (node->right != nullptr )
que. push (node->right);
}
}
// 释放二叉树内存
void deleteTree ( TreeNode * root )
{
if (root == nullptr ) return ;
deleteTree (root->left);
deleteTree (root->right);
delete root;
}
int main ()
{
// 构建二叉树
// F
// / \
// B G
// / \ / \
// A D I H
// / \
// C E
TreeNode * root = new TreeNode ( 'F' );
root->left = new TreeNode ( 'B' );
root->right = new TreeNode ( 'G' );
root->left->left = new TreeNode ( 'A' );
root->left->right = new TreeNode ( 'D' );
root->left->right->left = new TreeNode ( 'C' );
root->left->right->right = new TreeNode ( 'E' );
root->right->left = new TreeNode ( 'I' );
root->right->right = new TreeNode ( 'H' );
// 前序遍历
vector <char> preOrderResult;
preOrder (root, preOrderResult);
cout << "前序遍历: " << vectorToString (preOrderResult) << endl;
// 中序遍历
vector <char> inOrderResult;
inOrder (root, inOrderResult);
cout << "中序遍历: " << vectorToString (inOrderResult) << endl;
// 后序遍历
vector <char> postOrderResult;
postOrder (root, postOrderResult);
cout << "后序遍历: " << vectorToString (postOrderResult) << endl;
// 层序遍历
vector <char> levelOrderResult;
levelOrder (root, levelOrderResult);
cout << "层序遍历: " << vectorToString (levelOrderResult) << endl;
// 释放内存
deleteTree (root);
return 0 ;
}
前序遍历: [F, B, A, D, C, E, G, I, H] 中序遍历: [A, B, C, D, E, F, I, G, H] 后序遍历: [A, C, E, D, B, I, H, G, F] 层序遍历: [F, B, G, A, D, I, H, C, E]
前序遍历(PreOrder) :F, B, A, D, C, E, G, I, H
访问顺序:根 -> 左 -> 右
先访问根节点F,然后遍历左子树,最后遍历右子树
中序遍历(InOrder) :A, B, C, D, E, F, I, G, H
访问顺序:左 -> 根 -> 右
先遍历左子树,然后访问根节点,最后遍历右子树
后序遍历(PostOrder) :A, C, E, D, B, I, H, G, F
访问顺序:左 -> 右 -> 根
先遍历左子树,然后遍历右子树,最后访问根节点
层序遍历(LevelOrder) :F, B, G, A, D, I, H, C, E
访问顺序:按层从左到右
使用队列实现,先访问根节点,然后逐层访问
(
nullptr
) {}
};
// 辅助函数:打印整数向量
string vectorToString ( const vector < int > & vec )
{
if (vec. empty ()) return "[]" ;
stringstream ss;
ss << "[" ;
for ( size_t i = 0 ; i < vec. size (); i ++ )
{
ss << vec[i];
if (i < vec. size () - 1 ) ss << ", " ;
}
ss << "]" ;
return ss. str ();
}
// 根据前序和中序遍历序列重建二叉树
TreeNode * buildTree ( const vector < int > & preorder , const vector < int > & inorder ,
int preStart , int preEnd ,
int inStart , int inEnd ,
const unordered_map < int , int > & inMap )
{
if (preStart > preEnd || inStart > inEnd)
return nullptr ;
// 前序遍历的第一个元素是根节点
int rootVal = preorder[preStart];
TreeNode * root = new TreeNode (rootVal);
// 在中序遍历中找到根节点的位置
int rootIndex = inMap. at (rootVal);
int leftSize = rootIndex - inStart;
// 递归构建左子树和右子树
root->left = buildTree (preorder, inorder,
preStart + 1 , preStart + leftSize,
inStart, rootIndex - 1 , inMap);
root->right = buildTree (preorder, inorder,
preStart + leftSize + 1 , preEnd,
rootIndex + 1 , inEnd, inMap);
return root;
}
TreeNode * buildTreeFromPreIn ( const vector < int > & preorder , const vector < int > & inorder )
{
// 创建中序遍历的索引映射,加速查找
unordered_map <int , int> inMap;
for ( size_t i = 0 ; i < inorder. size (); i ++ )
{
inMap[inorder[i]] = i;
}
return buildTree (preorder, inorder, 0 , preorder. size () - 1 ,
0 , inorder. size () - 1 , inMap);
}
// 后序遍历
void postOrder ( TreeNode * root , vector < int > & result )
{
if (root == nullptr ) return ;
postOrder (root->left, result);
postOrder (root->right, result);
result. push_back (root->val);
}
// 层序遍历
void levelOrder ( TreeNode * root , vector < int > & result )
{
if (root == nullptr ) return ;
queue < TreeNode *> que;
que. push (root);
while ( ! que. empty ())
{
TreeNode * node = que. front ();
que. pop ();
result. push_back (node->val);
if (node->left != nullptr )
que. push (node->left);
if (node->right != nullptr )
que. push (node->right);
}
}
// 释放二叉树内存
void deleteTree ( TreeNode * root )
{
if (root == nullptr ) return ;
deleteTree (root->left);
deleteTree (root->right);
delete root;
}
int main ()
{
vector <int> preorder = { 1 , 2 , 4 , 5 , 3 , 6 , 7 };
vector <int> inorder = { 4 , 2 , 5 , 1 , 6 , 3 , 7 };
cout << "前序遍历: " << vectorToString (preorder) << endl;
cout << "中序遍历: " << vectorToString (inorder) << endl;
cout << endl;
// 重建二叉树
TreeNode * root = buildTreeFromPreIn (preorder, inorder);
// 推导后序遍历
vector <int> postOrderResult;
postOrder (root, postOrderResult);
cout << "后序遍历: " << vectorToString (postOrderResult) << endl;
// 推导层序遍历
vector <int> levelOrderResult;
levelOrder (root, levelOrderResult);
cout << "层序遍历: " << vectorToString (levelOrderResult) << endl;
cout << endl;
cout << "二叉树结构:" << endl;
cout << " 1" << endl;
cout << " / \\ " << endl;
cout << " 2 3" << endl;
cout << " / \\ / \\ " << endl;
cout << " 4 5 6 7" << endl;
// 释放内存
deleteTree (root);
return 0 ;
}
前序遍历: [1, 2, 4, 5, 3, 6, 7] 中序遍历: [4, 2, 5, 1, 6, 3, 7]
后序遍历: [4, 5, 2, 6, 7, 3, 1] 层序遍历: [1, 2, 3, 4, 5, 6, 7]
二叉树结构: 1 / \ 2 3 / \ / \ 4 5 6 7
重建过程 :
前序遍历的第一个元素 1 是根节点
在中序遍历中找到 1 的位置,左边 [4, 2, 5] 是左子树,右边 [6, 3, 7] 是右子树
递归构建左子树和右子树
后序遍历序列 :4, 5, 2, 6, 7, 3, 1
左子树:4, 5, 2
右子树:6, 7, 3
根节点:1
层序遍历序列 :1, 2, 3, 4, 5, 6, 7
唯一性 :前序遍历和中序遍历序列可以唯一确定二叉树的结构
cout
<<
" 原因:显式栈需要存储所有节点"
<<
endl;
cout << " - BFS: O(n)" << endl;
cout << " 原因:队列在最坏情况下需要存储所有节点" << endl;
cout << endl;
cout << "情况B:完全二叉树(高度 ⌊log₂n⌋)" << endl;
cout << " - DFS(递归实现): O(log n)" << endl;
cout << " 原因:递归调用栈的深度等于树的高度 ⌊log₂n⌋" << endl;
cout << " - DFS(迭代实现): O(log n)" << endl;
cout << " 原因:显式栈在最坏情况下存储一条路径,长度为树的高度" << endl;
cout << " - BFS: O(n)" << endl;
cout << " 原因:队列在最坏情况下需要存储最后一层的所有节点(约 n/2 个)" << endl;
cout << endl;
cout << "情况C:满二叉树(高度 ⌊log₂n⌋)" << endl;
cout << " - DFS(递归实现): O(log n)" << endl;
cout << " 原因:递归调用栈的深度等于树的高度 ⌊log₂n⌋" << endl;
cout << " - DFS(迭代实现): O(log n)" << endl;
cout << " 原因:显式栈在最坏情况下存储一条路径,长度为树的高度" << endl;
cout << " - BFS: O(n)" << endl;
cout << " 原因:队列在最坏情况下需要存储最后一层的所有节点(约 n/2 个)" << endl;
cout << endl;
cout << "总结:" << endl;
cout << " - 递归DFS的空间复杂度主要取决于树的高度" << endl;
cout << " - 迭代DFS的空间复杂度也取决于树的高度(显式栈)" << endl;
cout << " - BFS的空间复杂度主要取决于最宽层的节点数" << endl;
return 0 ;
}
=== 二叉树遍历的空间复杂度分析 ===
情况A:链状树(高度 n-1) - DFS(递归实现): O(n) 原因:递归调用栈的深度等于树的高度 n-1 - DFS(迭代实现): O(n) 原因:显式栈需要存储所有节点 - BFS: O(n) 原因:队列在最坏情况下需要存储所有节点
情况B:完全二叉树(高度 ⌊log₂n⌋) - DFS(递归实现): O(log n) 原因:递归调用栈的深度等于树的高度 ⌊log₂n⌋ - DFS(迭代实现): O(log n) 原因:显式栈在最坏情况下存储一条路径,长度为树的高度 - BFS: O(n) 原因:队列在最坏情况下需要存储最后一层的所有节点(约 n/2 个)
情况C:满二叉树(高度 ⌊log₂n⌋) - DFS(递归实现): O(log n) 原因:递归调用栈的深度等于树的高度 ⌊log₂n⌋ - DFS(迭代实现): O(log n) 原因:显式栈在最坏情况下存储一条路径,长度为树的高度 - BFS: O(n) 原因:队列在最坏情况下需要存储最后一层的所有节点(约 n/2 个)
总结: - 递归DFS的空间复杂度主要取决于树的高度 - 迭代DFS的空间复杂度也取决于树的高度(显式栈) - BFS的空间复杂度主要取决于最宽层的节点数
链状树(情况A) :
DFS(递归):O(n),递归调用栈深度为 n-1
DFS(迭代):O(n),显式栈需要存储所有节点
BFS:O(n),队列需要存储所有节点
完全二叉树(情况B) :
DFS(递归):O(log n),递归调用栈深度为树的高度
DFS(迭代):O(log n),显式栈存储一条路径
BFS:O(n),队列需要存储最后一层的所有节点
满二叉树(情况C) :
关键点 :
DFS的空间复杂度主要取决于树的高度
BFS的空间复杂度主要取决于最宽层的节点数
对于平衡树,DFS的空间复杂度更优(O(log n) vs O(n))