4 / 15

深层神经网络 - L层网络的构建 | 自在学

深层神经网络

2012年，AlexNet以压倒性优势赢得ImageNet图像识别竞赛，错误率比第二名低10个百分点。这个网络有8层。2015年，ResNet将层数推到152层，错误率降到3.6%，超越了人类水平。同年，Google的Inception v3有48层。深度学习的“深度”不是修辞，而是字面意义——更深的网络带来更强的表达能力。

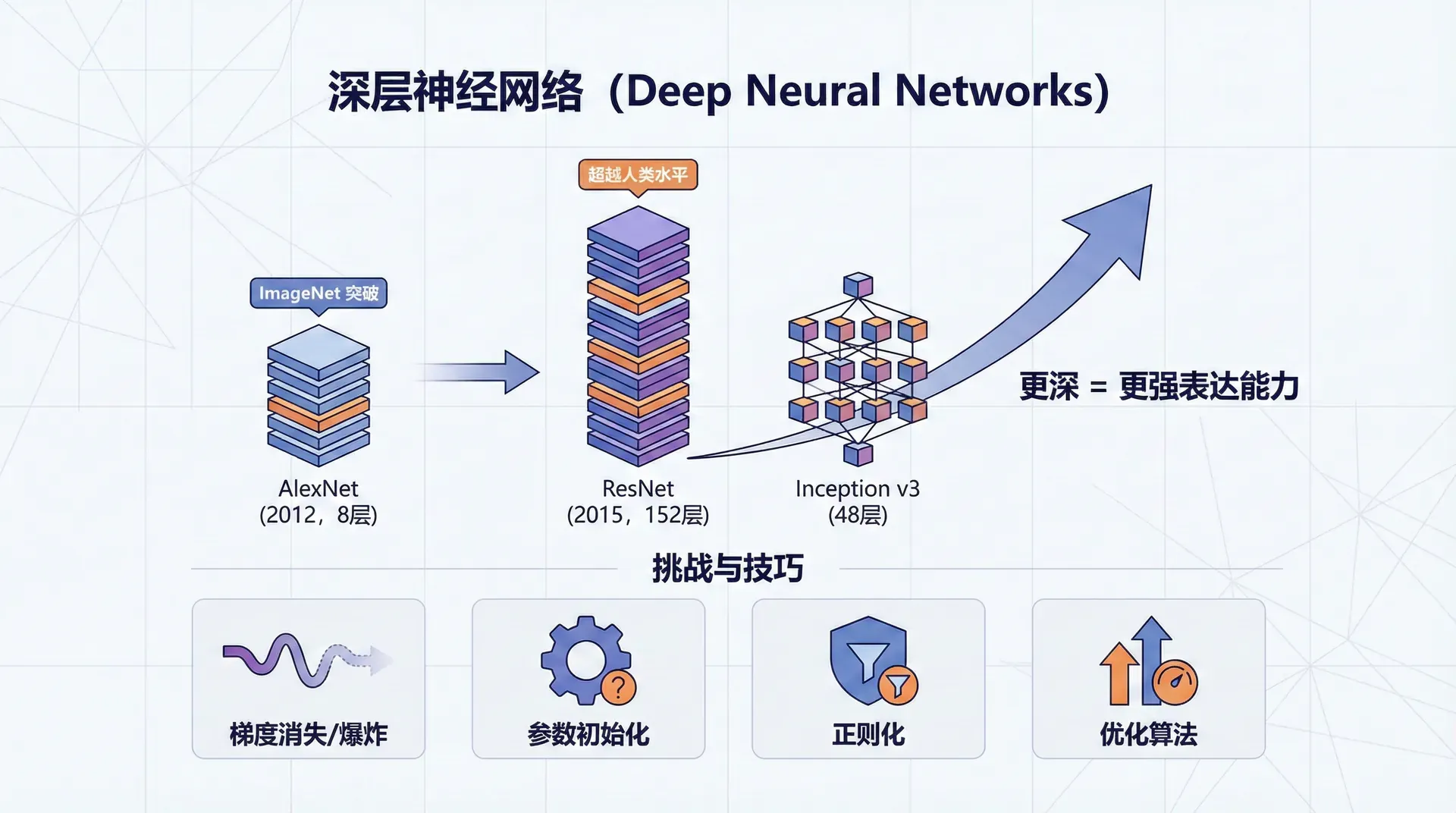
深层神经网络

但深度带来了新的挑战。如何有效地训练几十层甚至上百层的网络？梯度如何在这么多层间传播而不消失或爆炸？参数初始化、正则化、优化算法都需要重新审视。本节我们将从两层网络推广到任意L层网络，理解深层架构的设计原则和训练技巧。

从浅到深：推广到L层

上一节的两层网络是特例：一个隐藏层加一个输出层。推广到L层很自然——只是重复这个过程：

第1层： $Z^{[1]} = W^{[1]} X + b^{[1]}, \quad A^{[1]} = g^{[1]}(Z^{[1]})$

第2层： $Z^{[2]} = W^{[2]} A^{[1]} + b^{[2]}, \quad A^{[2]} = g^{[2]}(Z^{[2]})$

...

第L层： $Z^{[L]} = W^{[L]} A^{[L-1]} + b^{[L]}, \quad A^{[L]} = g^{[L]}(Z^{[L]})$

符号约定保持一致：

$L$ ：总层数（不包括输入层）
$n^{[l]}$ ：第 $l$ 层的神经元数
$W^{[l]} \in \mathbb{R}^{n^{[l]} \times n^{[l-1]}}$ ：第层的权重矩阵

一个4层网络（3个隐藏层 + 1个输出层）的结构：输入 → 第1隐藏层（5个神经元）→ 第2隐藏层（4个神经元）→ 第3隐藏层（3个神经元）→ 输出（1个神经元）。

数据流动的方向很清楚： $X \rightarrow A^{[1]} \rightarrow A^{[2]} \rightarrow A^{[3]} \rightarrow A^{[4]} = \hat{Y}$ 。每一层都是相同的模式：线性变换 + 非线性激活。

L层网络的前向传播

前向传播就是逐层计算，从输入到输出。对于 $l = 1, 2, \ldots, L$ ：

Z^{[l]} = W^{[l]} A^{[l-1]} + b^{[l]}

A^{[l]} = g^{[l]}(Z^{[l]})

其中 $A^{[0]} = X$ （输入）， $g^{[l]}$ 是第 $l$ 层的激活函数。

实现时，可以用一个for循环遍历所有层：

|
def L_model_forward(X, parameters):
    """
    L层神经网络的前向传播
    
    X: shape (n_x, m)
    parameters: 字典，包含所有层的W和b
    
    返回：
    AL: 最后一层的激活值
    caches: 每层的中间值列表，供反向传播使用
    """
    caches = []
    A = X
    L = len(parameters) // 2  # 层数（W和b成对）
    
    # 前L-1层：通常使用ReLU激活
    for l in range(1, L):

注意我们缓存了每层的 $A^{[l-1]}, W^{[l]}, b^{[l]}, Z^{[l]}$ 。这些值在反向传播时需要用到。

L层网络的反向传播

反向传播从输出层开始，逐层向输入层传播梯度。对于第 $l$ 层，假设我们已经计算出 $dZ^{[l]} = \frac{\partial \mathcal{L}}{\partial Z^{[l]}}$ ，则：

dW^{[l]} = \frac{1}{m} dZ^{[l]} (A^{[l-1]})^T

db^{[l]} = \frac{1}{m} \sum_{i=1}^m dz_i^{[l]}

dA^{[l-1]} = (W^{[l]})^T dZ^{[l]}

然后用链式法则计算 $dZ^{[l-1]}$ ：

dZ^{[l-1]} = dA^{[l-1]} \odot g^{[l-1]'}(Z^{[l-1]})

这里 $g^{[l-1]'}$ 是第 $l-1$ 层激活函数的导数。对于ReLU，导数是 $\mathbb{1}(Z > 0)$ （大于0则为1，否则为0）。

|
def L_model_backward(AL, Y, caches):
    """
    L层神经网络的反向传播
    
    AL: 输出层激活值，shape (1, m)
    Y: 真实标签，shape (1, m)
    caches: 前向传播缓存的每层中间值
    
    返回：
    grads: 所有层的梯度字典
    """
    grads = {}
    L = len(caches)
    m = AL.shape[1]
    Y = Y.reshape(AL.shape)
    
    # 输出层梯度（假设使用交叉熵损失 + Sigmoid激活）
    dAL =

反向传播的核心是链式法则的重复应用。每一层都将梯度传递给前一层，同时计算自己的参数梯度。

矩阵维度检验技巧

在实现深度网络时，矩阵维度错误是最常见的bug。一个有用的技巧是在关键操作后加assert检查：

|
# 前向传播中
Z = np.dot(W, A_prev) + b
assert Z.shape == (n_l, m), f"Z shape should be ({n_l}, {m}), got {Z.shape}"
 
# 反向传播中
dW = (1/m) * np.dot(dZ, A_prev.T)
assert dW.shape == W.shape,

为什么深层网络更有效

理论上，一个足够宽的单隐藏层网络可以逼近任意函数（万能逼近定理）。但实践中，深层网络往往比浅层宽网络更高效。为什么？

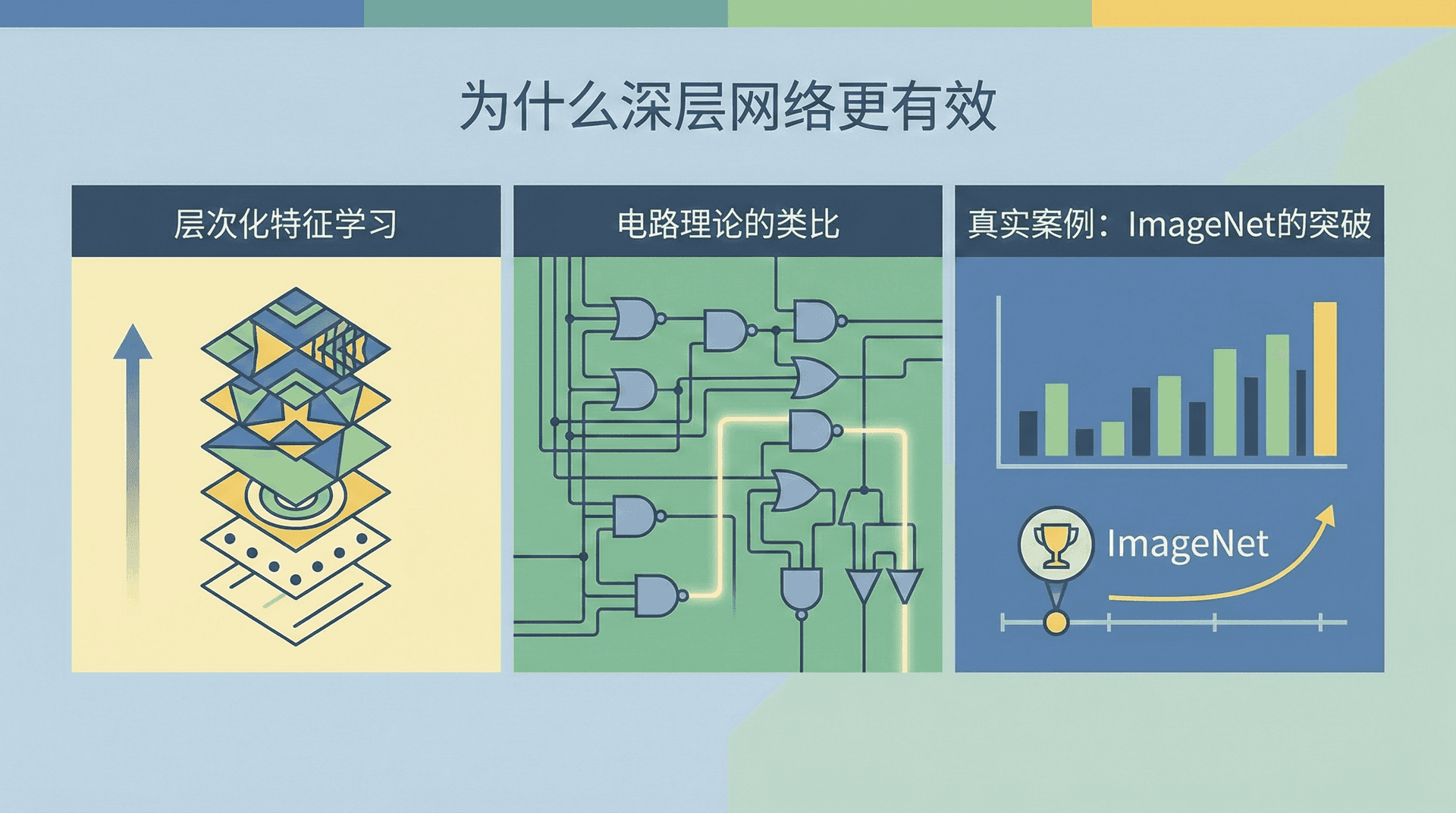
层次化特征学习

深层网络能够学习层次化的表示。以人脸识别为例：

第1层学习简单特征：边缘、颜色块
第2层组合边缘形成局部特征：眼睛、鼻子的轮廓
第3层组合局部特征：脸部的组成部分
第4层识别完整人脸

这种从简单到复杂的层次结构，类似于人类视觉系统的工作方式。浅层负责检测基本元素，深层负责组合这些元素。

电路理论的类比

从计算复杂性理论看，深层网络可以用更少的单元表达复杂函数。考虑计算一个布尔函数 $y = x_1 \text{ XOR } x_2 \text{ XOR } \cdots \text{ XOR } x_n$ 。用树状结构（深度为 $\log$ ）只需要个门，但如果限制深度为1（只有一层），可能需要指数级的门。

类似地，深层网络能用更紧凑的方式表示某些函数。这意味着更少的参数、更快的训练、更好的泛化。

真实案例：ImageNet的突破

2012年的AlexNet有8层，相比当时主流的浅层模型，它用1/10的参数达到了更好的效果。2014年的VGGNet将深度推到19层，2015年的ResNet达到152层。每次深度的跨越都伴随着性能的显著提升。这不是偶然，而是深层结构带来的根本优势。

参数与超参数

训练神经网络需要设置很多选择，理解参数与超参数的区别很重要。

参数（Parameters）是模型通过训练学习的量：

权重矩阵 $W^{[l]}$
偏置向量 $b^{[l]}$

这些值从数据中学习得到，是模型的"记忆"。

超参数（Hyperparameters）是在训练前人为设定的量：

学习率 $\alpha$
迭代次数（epochs）
隐藏层数 $L$
每层神经元数 $n^{[l]}$
激活函数的选择
正则化参数 $\lambda$

超参数控制学习过程本身。选择不当的超参数可能导致训练失败（如学习率太大）或效果不佳（如网络太浅）。

调整超参数是深度学习工程的重要部分。通常的流程是：

从一组合理的默认值开始（如学习率0.01，2-3层隐藏层）
训练模型，观察代价函数曲线
根据表现调整：代价不降就减小学习率，欠拟合就增加网络容量
重复直到满意

自动化的超参数搜索（如网格搜索、随机搜索、贝叶斯优化）可以节省人力，但需要大量计算资源。在后续课程中，我们会详细讨论超参数调优的策略。

深度学习与神经科学的关系

“神经网络”这个名字来源于对生物神经系统的模拟，但现代深度学习与神经科学的关系已经很弱。

相似之处

基本计算单元（人工神经元 vs 生物神经元）都接收输入，经过非线性变换产生输出
都是通过连接权重的调整来学习
都有层次化结构

不同之处

生物神经元远比人工神经元复杂：有树突、轴突等复杂结构，化学信号和电信号都参与
大脑的学习机制与反向传播不同：没有证据表明大脑使用梯度下降
人工神经网络是静态的前馈计算，大脑是动态的循环系统

Andrew Ng有句名言：“将深度学习类比为大脑，就像将飞机类比为鸟。飞机的灵感来自鸟，但我们不是通过模拟羽毛来制造飞机的。”深度学习的发展越来越依赖数学、优化理论、统计学习理论，而不是神经科学。

但神经科学仍然有启发意义。例如，注意力机制的灵感部分来自人类视觉注意力；ReLU激活函数受到生物神经元稀疏激活的启发。未来深度学习可能会从神经科学汲取更多灵感，但两者已经是独立发展的学科。

完整实现：训练L层神经网络

整合前面的组件，这里是一个完整的深度神经网络实现：

|
def initialize_parameters_deep(layer_dims):
    """
    初始化L层网络的参数
    
    layer_dims: list，每层的神经元数，如[n_x, n_h1, n_h2, ..., n_y]
    """
    np.random.seed(3)
    parameters = {}
    L = len(layer_dims)
    
    for l in range(1, L):
        parameters[f'W{l}'] = np.random.randn(layer_dims[l], layer_dims[l-

从理论到实践的跨越

我们现在掌握了构建和训练任意深度神经网络的完整工具链。但理论上可行不等于实践中有效。深层网络的训练面临诸多挑战：

梯度消失与爆炸：在反向传播中，梯度需要经过很多层的链式乘法。如果权重太小，梯度会指数级衰减（梯度消失），导致浅层几乎不更新。如果权重太大，梯度会指数级增长（梯度爆炸），导致数值溢出。
过拟合：深层网络参数众多，很容易记住训练数据的所有细节，但在新数据上表现差。这需要正则化技术。
训练速度：深层网络计算量大，每次迭代可能需要几秒甚至几分钟。更高效的优化算法（如Adam）、批归一化（Batch Normalization）等技术能显著加速训练。

在接下来的几节课中，我们将系统地学习这些实践技巧：正则化防止过拟合、更先进的优化算法、批归一化稳定训练、超参数调优策略等。这些技巧是让深度学习在真实项目中发挥作用的关键。

掌握了这些，你就能够构建和训练真正强大的深度神经网络，解决图像识别、自然语言处理等复杂问题。深度学习的大门已经打开，让我们继续前进。

n

\log n