首页课程创意工坊价格

3 / 15

深层神经网络

浅层神经网络 - 从单层到多层 | 自在学

浅层神经网络

逻辑回归能够学习线性决策边界，但真实世界的问题往往不是线性可分的。想象一个简单的异或（XOR）问题：当两个输入相同时输出0，不同时输出1。画在平面上，这四个点无法用一条直线分开。逻辑回归在这个问题上完全无能为力。

解决方案是在输入和输出之间加入隐藏层（Hidden Layer）。这一层的神经元能够学习输入的非线性变换，将数据映射到一个新的表示空间。在那个空间里，原本线性不可分的数据可能变得可分。这就是神经网络能够逼近任意复杂函数的关键。

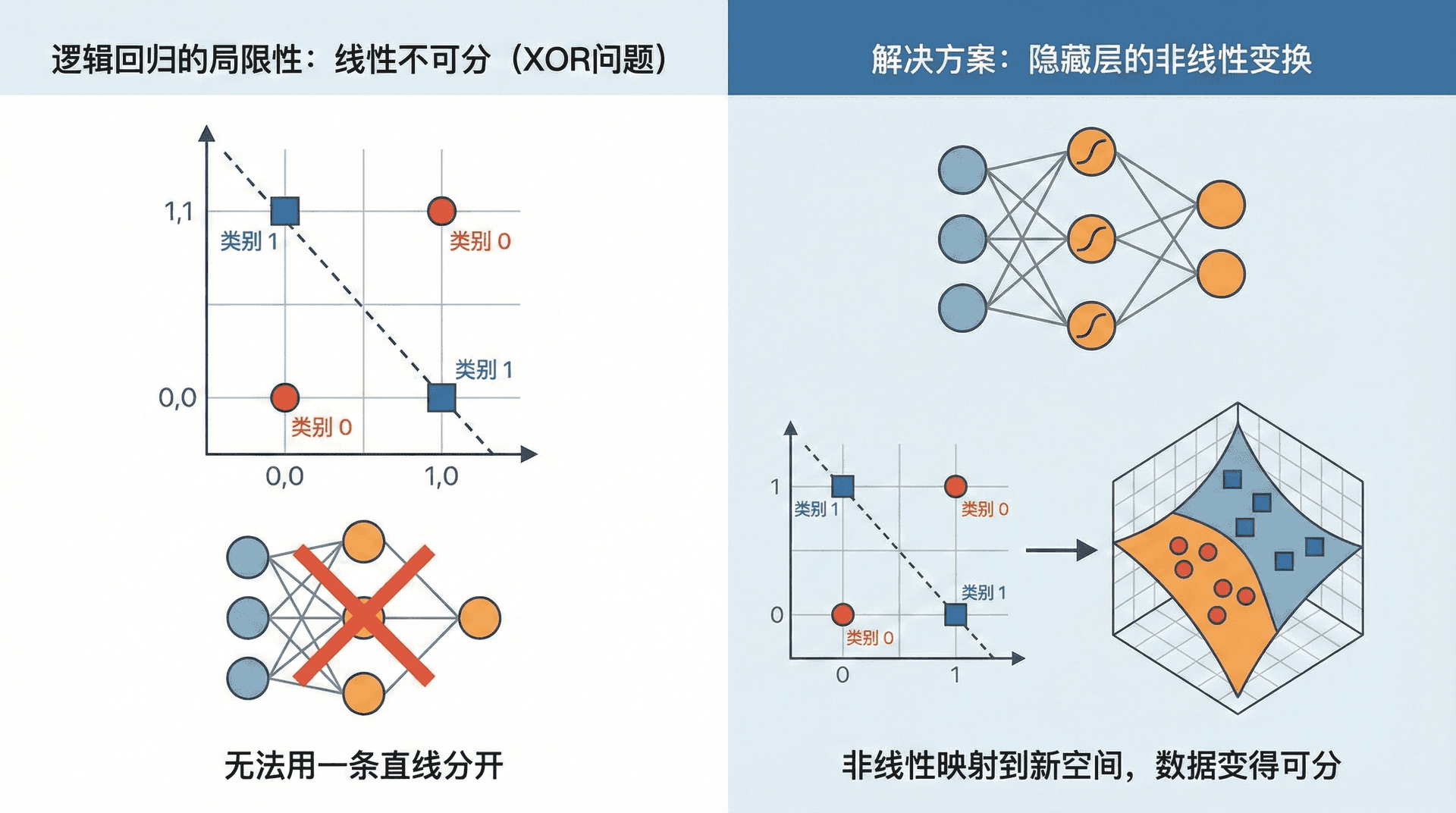
浅层神经网络

从单层到多层

让我们从逻辑回归出发，逐步构建一个包含隐藏层的神经网络。逻辑回归的计算过程是：

z = w^T x + b, \quad \hat{y} = \sigma(z)

现在我们在中间插入一个隐藏层，包含4个神经元：

这个网络有两层计算（隐藏层和输出层），通常称为"两层神经网络"。输入层不算在内，因为它只是数据的占位符，不做计算。

符号约定变得重要起来。用上标 $[l]$ 表示层数：

$W^{[1]}$ ：输入层到隐藏层的权重矩阵
$b^{[1]}$ ：隐藏层的偏置向量
$a^{[1]}$ ：隐藏层的激活值（activation）
：隐藏层到输出层的权重矩阵

隐藏层有4个神经元，输入有3个特征，因此 $W^{[1]} \in \mathbb{R}^{4 \times 3}$ ， $b^{[1]} \in \mathbb{R}^{4 \times 1}$ 。每一行对应一个神经元的权重。

前向传播：从输入到输出

给定一个输入样本 $x$ ，神经网络通过前向传播（Forward Propagation）计算输出。对于我们的两层网络：

隐藏层计算：

z^{[1]} = W^{[1]} x + b^{[1]}, \quad a^{[1]} = g^{[1]}(z^{[1]})

这里 $g^{[1]}$ 是隐藏层的激活函数（稍后讨论）。

输出层计算：

z^{[2]} = W^{[2]} a^{[1]} + b^{[2]}, \quad a^{[2]} = g^{[2]}(z^{[2]})

对于二分类，输出层通常使用Sigmoid激活： $a^{[2]} = \sigma(z^{[2]})$ ，这就是我们的预测 $\hat{y}$ 。

注意信息的流动： $x \rightarrow z^{[1]} \rightarrow a^{[1]} \rightarrow z^{[2]} \rightarrow a^{[2]} = \hat{y}$ 。每一层都先计算加权和（），再通过激活函数（）得到激活值（）。

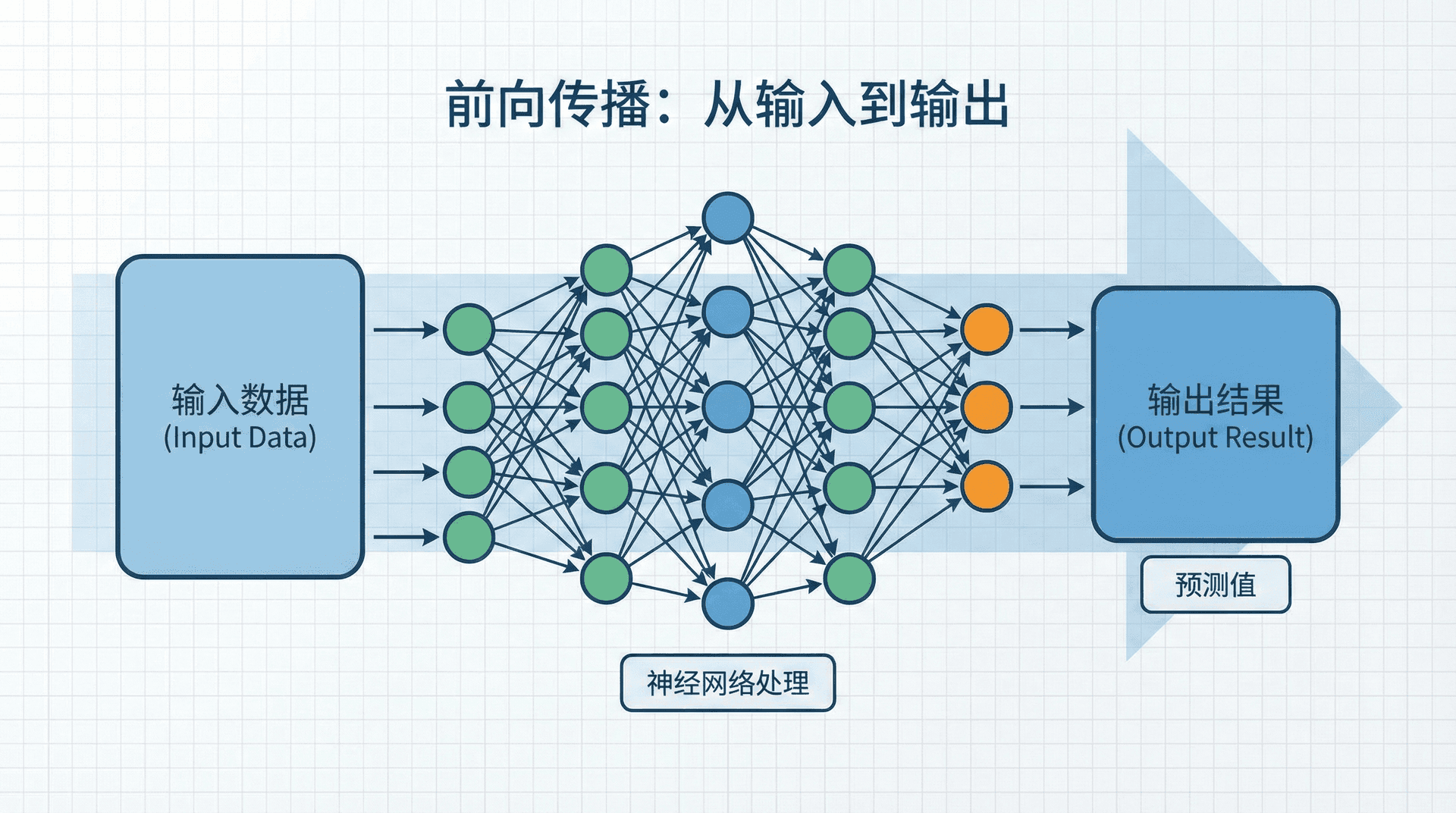
前向传播：从输入到输出

向量化：同时处理多个样本

前面是单个样本的情况。训练时我们有 $m$ 个样本，需要对每个样本执行前向传播。如果用for循环逐个处理，会非常慢。向量化让我们一次处理所有样本。

将所有样本按列堆叠成矩阵 $X \in \mathbb{R}^{n_x \times m}$ ，前向传播变成：

Z^{[1]} = W^{[1]} X + b^{[1]}, \quad A^{[1]} = g^{[1]}(Z^{[1]})

Z^{[2]} = W^{[2]} A^{[1]} + b^{[2]}, \quad A^{[2]} = g^{[2]}(Z^{[2]})

这里大写的 $Z^{[l]}$ 和 $A^{[l]}$ 是矩阵，每一列对应一个样本。激活函数 $g$ 逐元素应用。

|
def forward_propagation(X, parameters):
    """
    两层神经网络的前向传播
    
    X: 输入矩阵，shape (n_x, m)
    parameters: 包含W1, b1, W2, b2的字典
    
    返回：
    A2: 输出层激活值，shape (1, m)
    cache: 包含中间值的字典，供反向传播使用
    """
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']
    
    # 隐藏层

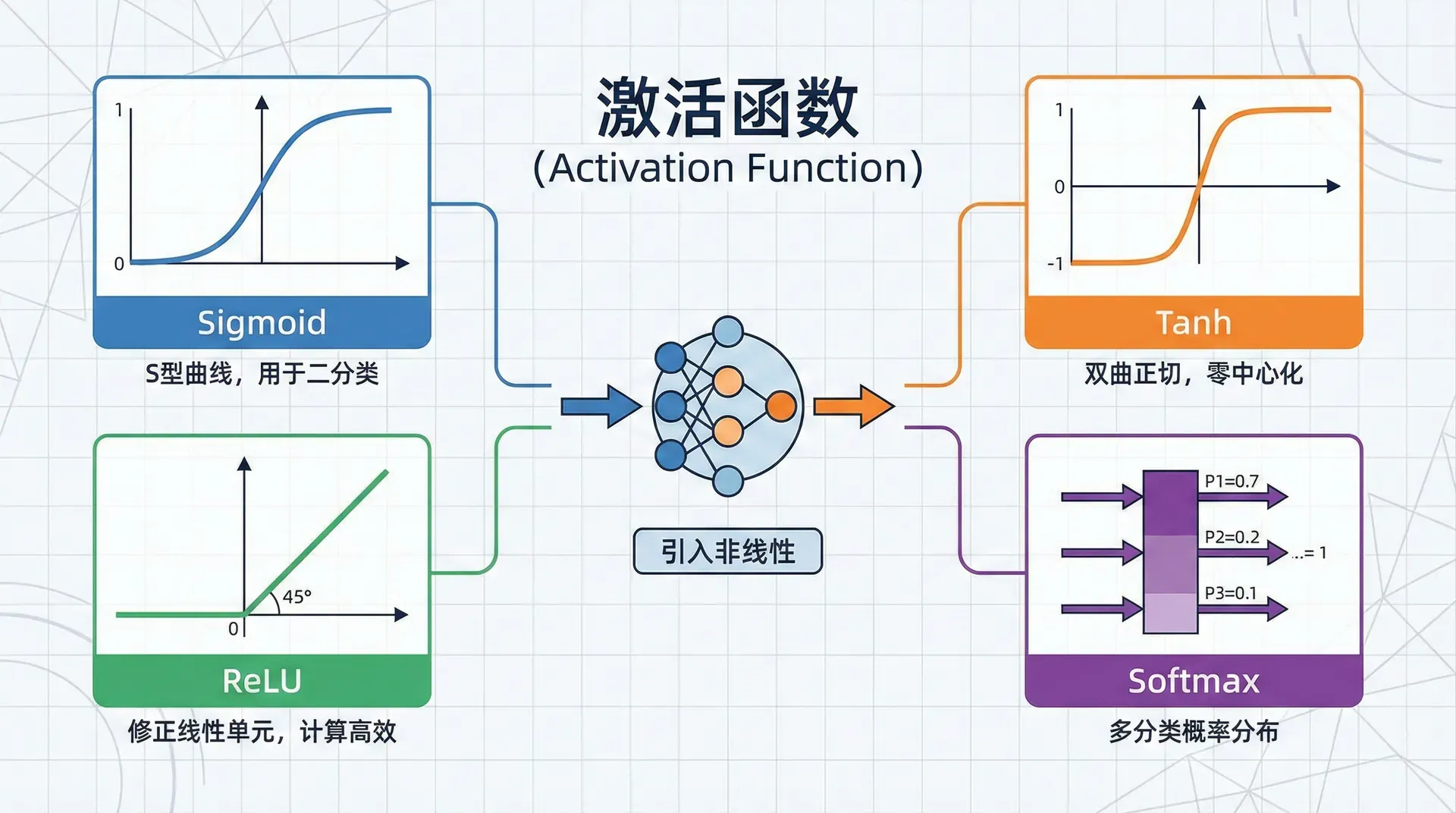
激活函数：引入非线性的关键

为什么需要激活函数？如果所有层都是线性变换，整个网络就退化为一个线性模型。数学上，多个线性变换的组合仍然是线性变换。假设隐藏层和输出层都不用激活函数：

a^{[1]} = W^{[1]} x + b^{[1]}, \quad a^{[2]} = W^{[2]} a^{[1]} + b^{[2]}

代入得：

a^{[2]} = W^{[2]}(W^{[1]} x + b^{[1]}) + b^{[2]} = (W^{[2]} W^{[1]}) x + (W^{[2]} b^{[1]} + b^{[2]})

这等价于一个单层网络！无论堆叠多少层，没有非线性激活，网络的表达能力不会增强。激活函数引入的非线性是神经网络能够学习复杂模式的根本原因。

常用激活函数

Sigmoid函数：

\sigma(z) = \frac{1}{1 + e^{-z}}, \quad \sigma'(z) = \sigma(z)(1 - \sigma(z))

输出在(0, 1)之间，可以解释为概率。但有两个问题：梯度饱和（当 $|z|$ 很大时梯度接近0）和输出不以0为中心。现在很少用在隐藏层，主要用于二分类的输出层。

Tanh函数：

\tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}, \quad \tanh'(z) = 1 - \tanh^2(z)

输出在(-1, 1)之间，以0为中心，通常比Sigmoid效果更好。但仍然存在梯度饱和问题。

ReLU（Rectified Linear Unit）：

\text{ReLU}(z) = \max(0, z), \quad \text{ReLU}'(z) = \begin{cases} 1 & \text{if } z > 0 \\ 0 & \text{if } z \leq 0 \end{cases}

ReLU是目前最常用的激活函数。优点是：计算简单，不会梯度饱和（正半轴梯度恒为1），训练速度快。缺点是“神经元死亡”问题——如果一个神经元的输出一直是负数，它的梯度永远是0，无法更新。

Leaky ReLU：

\text{LeakyReLU}(z) = \max(0.01z, z)

在负半轴有一个小的斜率（通常是0.01），避免了神经元死亡问题。

选择建议：

隐藏层：优先使用ReLU。如果遇到"死神经元"问题，尝试Leaky ReLU
输出层：二分类用Sigmoid，多分类用Softmax，回归用线性（无激活）

|
# 常用激活函数的NumPy实现
def sigmoid(Z):
    return 1 / (1 + np.exp(-Z))
 
def tanh(Z):
    return np.tanh(Z)
 
def relu(Z):
    return np.maximum(0, Z)
 
def leaky_relu(Z, alpha=0.01):
    return np.maximum(alpha * Z, Z)
 
# 对应的导数
def

为什么ReLU如此有效？

ReLU的成功有多个原因。首先，它缓解了梯度消失问题——Sigmoid和tanh在 $|z|$ 很大时梯度接近0，导致深层网络难以训练，而ReLU在正半轴梯度恒为1。其次，它引入了稀疏性——大约一半的神经元输出为0，这种稀疏表示接近生物神经元的行为，且计算高效。最后，ReLU的简单性让它计算更快，也更容易优化。

但ReLU不是万能的。在某些任务上，tanh或其他激活函数可能更好。实践中通常先尝试ReLU，效果不好再换。

反向传播：计算梯度

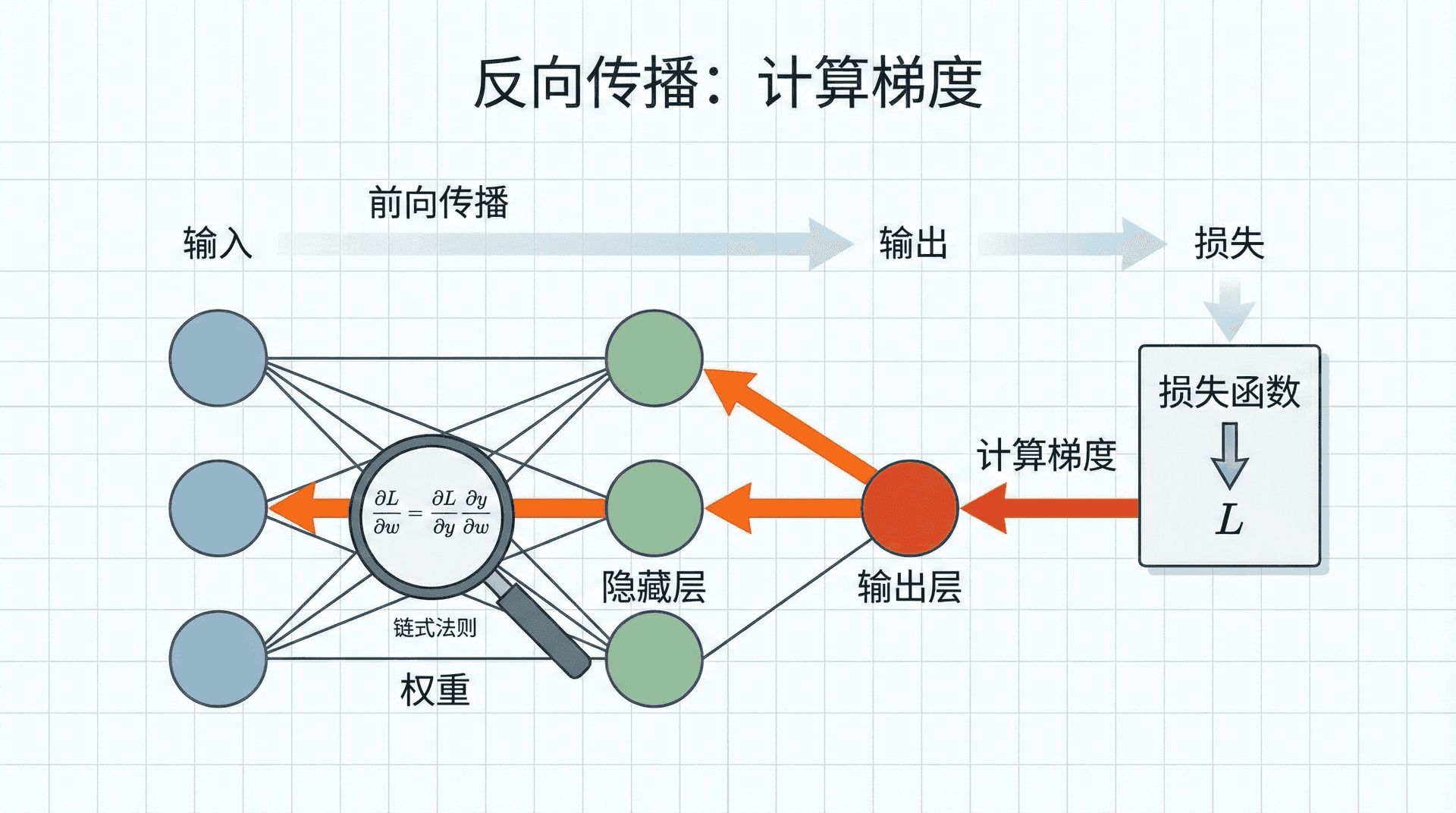
前向传播给出了预测，但我们需要梯度来更新参数。反向传播（Backpropagation）通过链式法则，从输出层逐层向输入层计算梯度。

对于两层网络，给定损失函数 $\mathcal{L}(a^{[2]}, y)$ ，反向传播的推导如下：

输出层的梯度：

dz^{[2]} = \frac{\partial \mathcal{L}}{\partial z^{[2]}} = a^{[2]} - y

（这里假设使用交叉熵损失和Sigmoid激活，推导过程我们在第2节见过）

dW^{[2]} = \frac{\partial \mathcal{L}}{\partial W^{[2]}} = dz^{[2]} \cdot (a^{[1]})^T

db^{[2]} = \frac{\partial \mathcal{L}}{\partial b^{[2]}} = dz^{[2]}

隐藏层的梯度：

首先通过链式法则计算 $dz^{[1]}$ ：

da^{[1]} = (W^{[2]})^T dz^{[2]}

dz^{[1]} = da^{[1]} \odot g^{[1]'}(z^{[1]})

这里 $\odot$ 表示逐元素乘法（Hadamard product）， $g^{[1]'}$ 是激活函数的导数。

dW^{[1]} = dz^{[1]} \cdot x^T

db^{[1]} = dz^{[1]}

向量化版本（处理 $m$ 个样本）：

dZ^{[2]} = A^{[2]} - Y

dW^{[2]} = \frac{1}{m} dZ^{[2]} (A^{[1]})^T

db^{[2]} = \frac{1}{m} \sum_{i=1}^m dz^{[2](i)}

dZ^{[1]} = (W^{[2]})^T dZ^{[2]} \odot g^{[1]'}(Z^{[1]})

dW^{[1]} = \frac{1}{m} dZ^{[1]} X^T

db^{[1]} = \frac{1}{m} \sum_{i=1}^m dz^{[1](i)}

|
def backward_propagation(parameters, cache, X, Y):
    """
    两层神经网络的反向传播
    
    parameters: 包含W1, b1, W2, b2
    cache: 前向传播缓存的中间值
    X: 输入，shape (n_x, m)
    Y: 标签，shape (1, m)
    
    返回梯度字典
    """
    m = X.shape[1]
    
    W1 = parameters['W1']
    W2 = parameters['W2']
    A1 = cache['A1']
    A2

权重初始化：不能全为零

训练神经网络前需要初始化参数。一个常见的错误是将所有权重初始化为0。这会导致"对称性"问题：如果所有神经元的权重相同，那么它们接收到的梯度也相同，更新后仍然相同。网络退化为只有一个神经元的状态。

正确的做法是随机初始化权重，打破对称性。偏置可以初始化为0（不会导致对称性问题）。

|
def initialize_parameters(n_x, n_h, n_y):
    """
    随机初始化参数
    
    n_x: 输入特征数
    n_h: 隐藏层神经元数
    n_y: 输出层神经元数
    """
    np.random.seed(2)  # 为了可复现性
    
    W1 = np.random.randn(n_h, n_x) * 0.01  # 小随机数
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros((n_y, 1))

这里乘以0.01是为了让初始权重较小。如果权重太大，使用Sigmoid或tanh激活时， $z$ 会落在饱和区，梯度接近0，训练很慢。

为什么乘以0.01？

这只是一个经验值。对于浅层网络和Sigmoid/tanh激活，0.01通常效果不错。但对于深层网络或ReLU激活，需要更精细的初始化策略（如Xavier初始化或He初始化），我们在后续课程中会详细讨论。

权重初始化看似小问题，实则非常关键。不当的初始化可能导致训练完全失败——梯度消失或梯度爆炸。

完整的训练流程

现在我们有了所有组件，可以训练一个完整的两层神经网络：

|
def nn_model(X, Y, n_h, num_iterations=10000, learning_rate=1.2, print_cost=False):
    """
    训练两层神经网络
    
    X: shape (n_x, m)
    Y: shape (1, m)
    n_h: 隐藏层神经元数
    """
    np.random.seed(3)
    n_x = X.shape[0]
    n_y = Y.shape[0]
    
    # 初始化参数
    parameters = initialize_parameters(n_x, n_h, n_y)

浅层网络的威力

即使只有一个隐藏层，神经网络已经能够学习复杂的非线性决策边界。理论上，一个足够宽的单隐藏层网络可以逼近任意连续函数（这被称为“万能逼近定理”）。

但实践中，深层网络往往比浅层宽网络更有效。一个3层的窄网络可能比一个1层的宽网络用更少的参数达到更好的效果。这是为什么呢？深层结构能够学习层次化的表示：浅层学习简单特征，深层组合这些特征学习复杂模式。这种层次化学习更接近人类的认知方式，也更数据高效。

在下一节中，我们将这个两层网络推广到任意多层，构建真正的“深度”神经网络。我们还将看到，虽然层数增加了，但训练的基本流程保持不变——只是前向传播和反向传播需要循环经过更多层而已。

W^{[2]}