5 / 15

深度学习的实践技巧 - 正则化与优化 | 自在学

深度学习的实践技巧

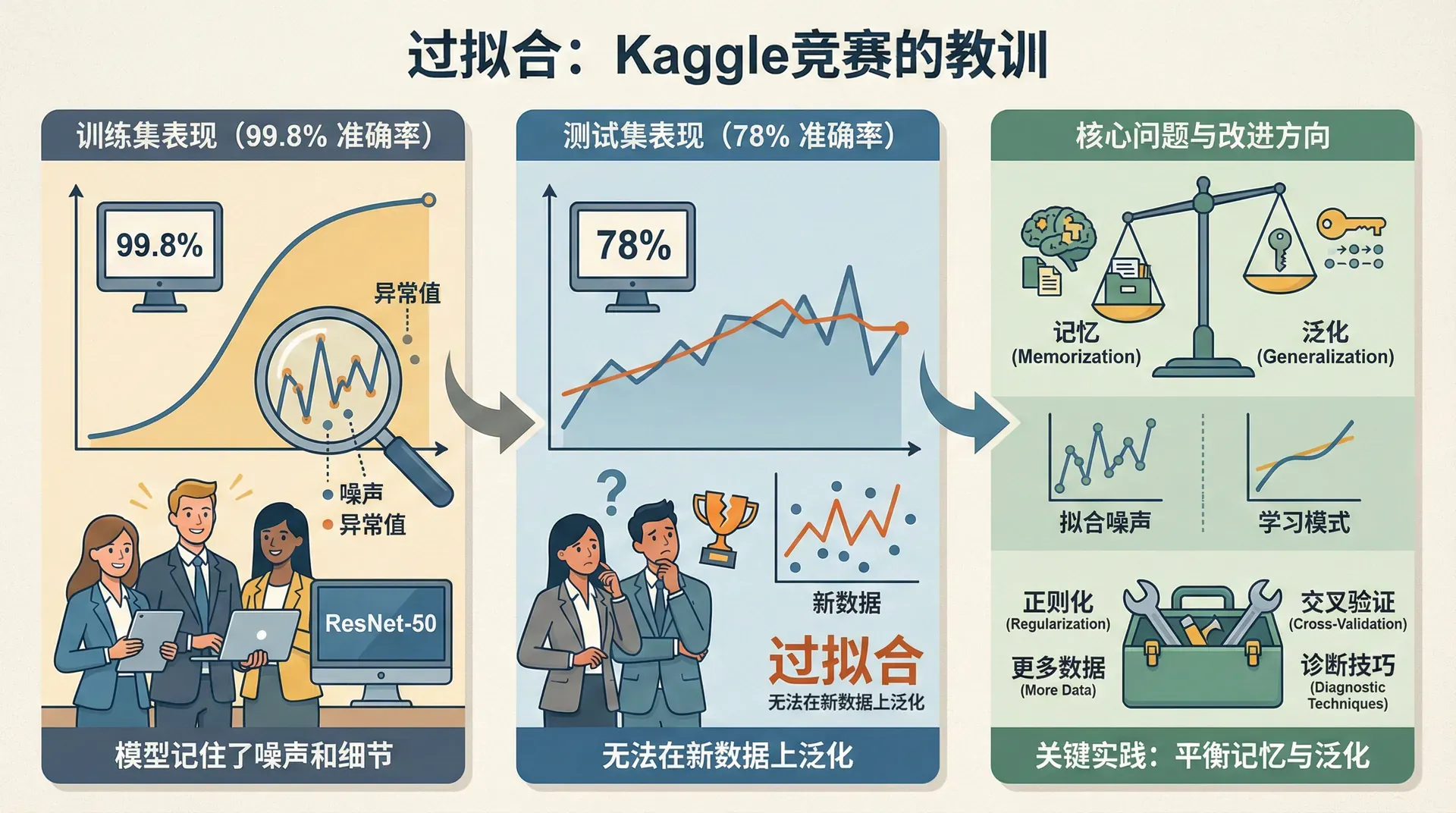
2017年Kaggle的一个图像分类竞赛中，一个参赛队伍训练了一个ResNet-50模型，在训练集上达到了99.8%的准确率，团队成员兴奋地认为他们稳拿冠军。但提交到测试集后，准确率只有78%，排名跌到第50名开外。这就是典型的过拟合——模型记住了训练数据的所有细节，包括噪声和异常值，但在新数据上完全无法泛化。

过拟合是深度学习实践中最常见的问题。模型参数可能有数百万个，而训练数据总是有限的。如何让模型学到真正的模式而非记忆训练数据？如何诊断模型的问题并有针对性地改进？这些实践技巧往往决定了项目的成败。

深度学习的实践技巧

数据集划分：训练、验证、测试

在传统机器学习时代，常见的做法是60/20/20划分：60%训练集，20%验证集，20%测试集。但在大数据时代，这个比例已经过时。

假设你有100万张图片。按传统划分，训练集60万，验证集20万，测试集20万。但验证集的目的是什么？是帮你选择超参数和模型架构。20万张图片远超这个需求——实际上，1万张就足够评估模型性能了。那剩下的19万张数据放在验证集就是浪费，它们应该用于训练。

现代推荐划分（百万级数据）：

训练集：98%（980,000张）
验证集：1%（10,000张）
测试集：1%（10,000张）

甚至可以是99.5/0.25/0.25。关键原则是：验证集和测试集只需要足够大到能可靠地评估性能即可。

但有一个关键约束：验证集和测试集必须来自同一分布。假设你在做一个手机App的猫识别功能：

训练集：网上下载的高质量猫图片
验证集和测试集：用户用手机拍摄的模糊、光线不好的照片

这样划分是合理的。但如果验证集是某个城市用户的照片，测试集是另一个城市的，分布不一致，在验证集上调优可能在测试集上失效。

为什么需要测试集？

你可能会想，有了验证集还要测试集干什么？这是因为：验证集用于调整超参数，模型会"适应"验证集的特性，导致在验证集上过度乐观。测试集作为最终的检验，不参与任何决策，给出无偏的性能估计。

在学术研究或竞赛中，测试集必不可少。但在一些工业项目中，如果数据量很小，可以省略测试集，只用训练集和验证集。

偏差与方差

模型训练完成，验证集准确率只有85%，不够理想。问题出在哪里？是模型太简单学不到模式（欠拟合），还是太复杂记住了训练数据（过拟合）？这需要通过偏差-方差分析来诊断。

偏差（Bias）衡量模型的拟合能力。高偏差意味着模型太简单，连训练数据都拟合不好——这是欠拟合。想象用一条直线去拟合一个复杂的曲线，无论如何调整都拟合不好。
方差（Variance）衡量模型的泛化能力。高方差意味着模型对训练数据的微小变化非常敏感——这是过拟合。模型记住了训练数据的细节，包括噪声，在新数据上表现差。

通过比较训练集和验证集的误差，可以诊断问题：

训练集误差	验证集误差	诊断	解决方案
1%	11%	高方差（过拟合）	更多数据、正则化、简化模型
15%	16%	高偏差（欠拟合）	更复杂模型、更多特征、更长训练
15%	30%	高偏差+高方差	先解决偏差，再解决方差
1%	2%	理想状态	继续优化或已足够好

这里假设人类水平（或贝叶斯误差）接近0%。如果任务本身就很难（如人类准确率也只有90%），那么15%的训练集误差可能是可接受的。

正则化

正则化通过限制模型复杂度，防止它过度拟合训练数据。最常用的是L2正则化和Dropout。

正则化

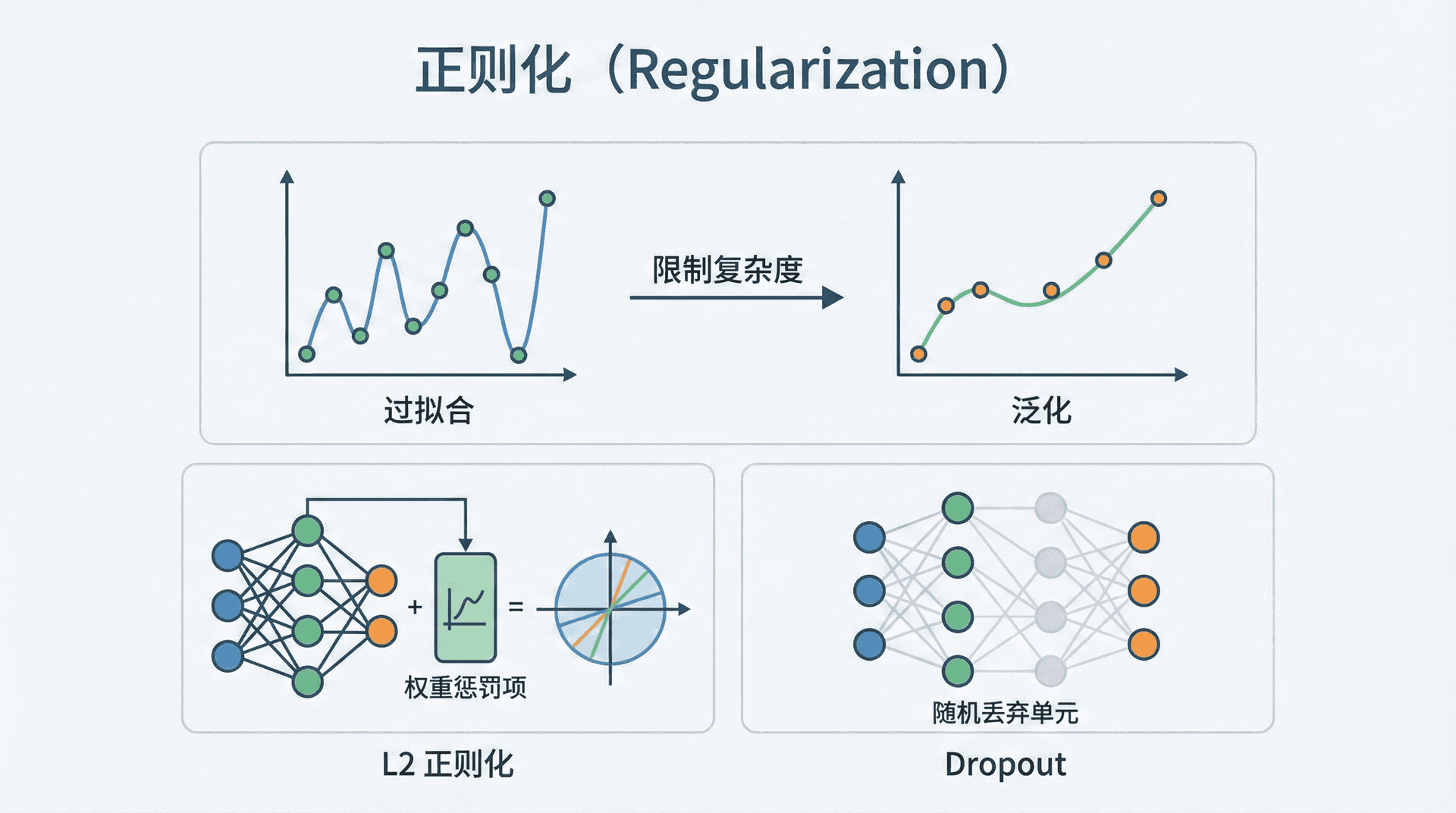
L2正则化（权重衰减）

在代价函数中添加一项，惩罚过大的权重：

J_{\text{reg}} = J + \frac{\lambda}{2m} \sum_{l=1}^{L} \|W^{[l]}\|_F^2

这里 $\|W^{[l]}\|_F^2$ 是Frobenius范数（所有元素的平方和）， $\lambda$ 是正则化强度。

更新规则变为：

W^{[l]} := W^{[l]} - \alpha \left( \frac{\partial J}{\partial W^{[l]}} + \frac{\lambda}{m} W^{[l]} \right) = \left(1 - \frac{\alpha \lambda}{m}\right) W^{[l]} - \alpha \frac{\partial J}{\partial W^{[l]}}

因子 $(1 - \frac{\alpha \lambda}{m})$ 小于1，每次更新时权重都会衰减一点，因此L2正则化也叫"权重衰减"。

为什么这能防止过拟合？大的权重意味着模型对输入的微小变化非常敏感，容易学到噪声。正则化压缩权重，让模型更平滑、更泛化。

|
def compute_cost_with_regularization(AL, Y, parameters, lambd):
    """计算带L2正则化的代价"""
    m = Y.shape[1]
    L = len(parameters) // 2
    
    # 交叉熵损失
    cross_entropy = -(1/m) * np.sum(Y * np.log(AL) + (1-Y) * np.log(1-AL))

Dropout：随机关闭神经元

Dropout在每次训练迭代时随机"关闭"一部分神经元（将它们的输出设为0）。比如设置keep_prob=0.8，则每个神经元有80%概率保留，20%概率被关闭。

为什么这有效？ Dropout强制网络不能依赖任何单个神经元，必须学习更鲁棒的特征组合。相当于训练了多个不同的子网络，最后集成它们的效果。

实现时使用Inverted Dropout技术，在训练时除以keep_prob，保持期望不变：

|
# 前向传播中（训练时）
A1 = relu(Z1)
D1 = np.random.rand(A1.shape[0], A1.shape[1]) < keep_prob  # dropout mask
A1 = A1 * D1  # 关闭一些神经元
A1 = A1 / keep_prob  # Inverted dropout：保持期望不变
 
# 测试时：不使用dropout，所有神经元都参与
A1 = relu(Z1)

Dropout通常用在参数很多的层（如全连接层）。卷积层参数较少，一般不用Dropout。输出层也不用。

Dropout的副作用

Dropout会让代价函数在训练过程中不单调下降——因为每次迭代使用不同的子网络。这让调试变难。建议：先不用Dropout训练，确认代价函数正常下降，再加上Dropout微调。

数据增强

更多训练数据几乎总能提升性能，但收集和标注数据成本高。数据增强通过对现有数据进行变换，人工增加数据量。

图像增强：

水平翻转（猫向左看和向右看都是猫）
随机裁剪和缩放
颜色抖动：调整亮度、对比度、饱和度
旋转（小角度，如±15度）

2015年ImageNet竞赛中，ResNet团队大量使用了数据增强，相当于将训练集扩大了10倍。

Early Stopping

监控验证集误差，当它不再下降时停止训练。这避免了过度训练——训练集误差继续下降但验证集误差开始上升的阶段。

Early Stopping虽然简单有效，但有个缺点：它同时影响了优化过程（何时停止）和正则化（防止过拟合），违背了"正交化"原则（一个机制只解决一个问题）。Andrew Ng更推荐L2正则化+训练到收敛，而不是Early Stopping。

归一化输入

输入归一化是个简单但重要的技巧。如果不同特征的尺度差异很大（如一个特征范围是0-1，另一个是0-10000），代价函数的等高线会变成狭长的椭圆，梯度下降需要很多次震荡才能收敛。

归一化包含两步：

零均值化： $X := X - \mu$ ，其中 $\mu = \frac{1}{m}\sum_{i=1}^m x^{(i)}$

归一化后，所有特征的均值为0，方差为1，代价函数变成圆形的等高线，训练更快。

|
def normalize_inputs(X):
    """归一化输入"""
    mu = np.mean(X, axis=1, keepdims=True)
    X = X - mu
    
    sigma = np.std(X, axis=1, keepdims=True)
    X = X / sigma
    
    return X, mu, sigma

梯度消失与爆炸

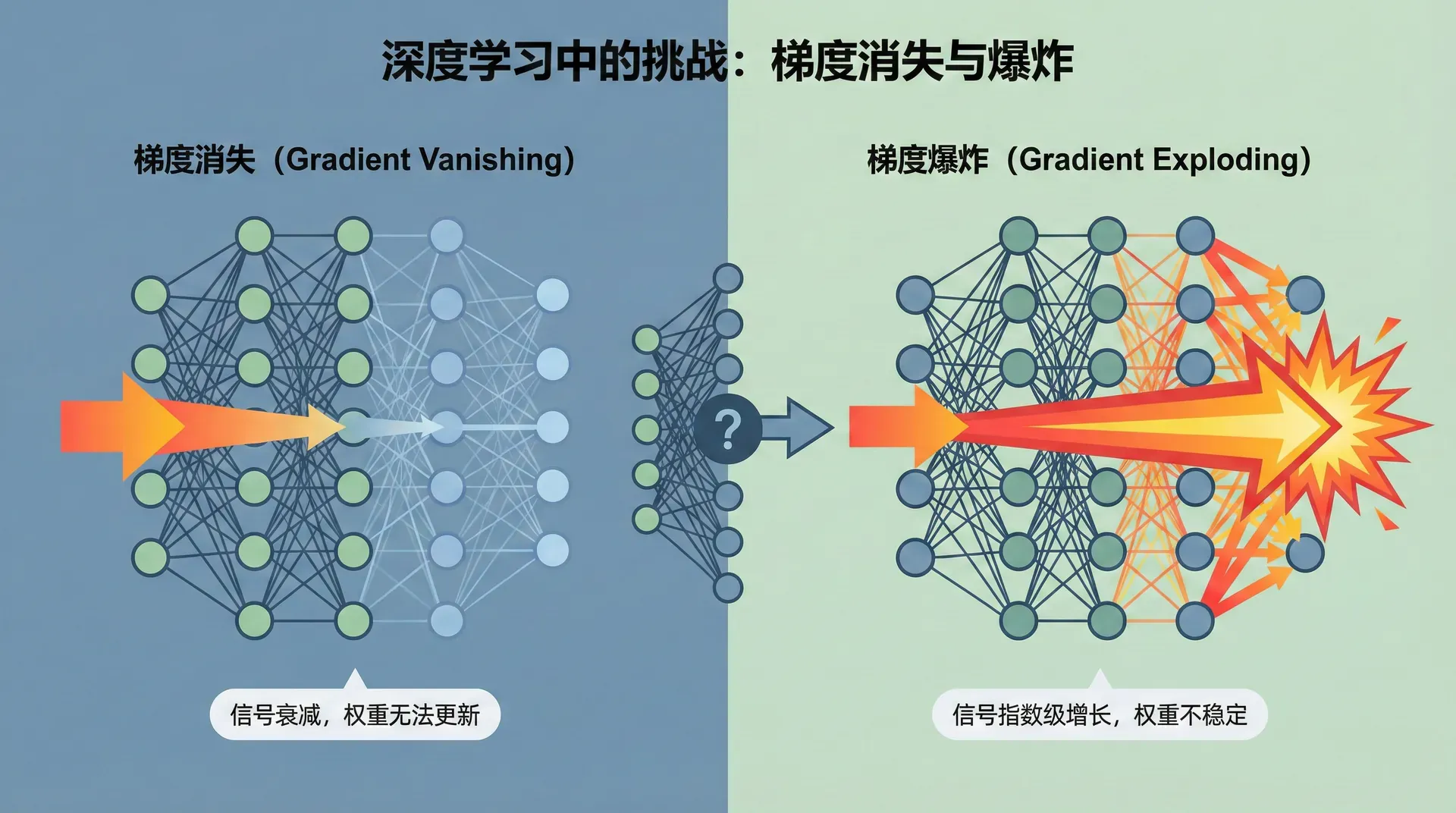
深层网络训练时常遇到梯度消失或梯度爆炸问题。考虑一个100层的网络，每层权重 $W^{[l]} = 1.5 \cdot I$ （稍大于单位矩阵）。经过100层，激活值会变成 $1.5^{100} \approx 10^{17}$ ——梯度爆炸。如果，激活值会变成 ——梯度消失。

解决方案是合适的权重初始化。对于ReLU激活，使用He初始化：

W^{[l]} \sim \mathcal{N}\left(0, \sqrt{\frac{2}{n^{[l-1]}}}\right)

对于tanh激活，使用Xavier初始化：

W^{[l]} \sim \mathcal{N}\left(0, \sqrt{\frac{1}{n^{[l-1]}}}\right)

原理是：保持每层激活值的方差大致相同，避免指数级增长或衰减。

|
def initialize_parameters_he(layers_dims):
    """He初始化（用于ReLU）"""
    parameters = {}
    L = len(layers_dims)
    
    for l in range(1, L):
        parameters[f'W{l}'] = np.random.randn(layers_dims[l], layers_dims[l-1]) * np.sqrt(2 / layers_dims[l-1])

梯度检验

实现反向传播容易出错，而错误可能很隐蔽——代价函数仍然下降，只是下降很慢或停在次优解。梯度检验能帮你发现这些bug。

原理是用数值方法近似梯度，与反向传播计算的梯度对比：

\frac{\partial J}{\partial \theta} \approx \frac{J(\theta + \epsilon) - J(\theta - \epsilon)}{2\epsilon}

双边差分的误差是 $O(\epsilon^2)$ ，比单边差分 $O(\epsilon)$ 更准确。

|
def gradient_check(parameters, gradients, X, Y, epsilon=1e-7):
    """
    梯度检验
    返回：相对误差。如果 < 1e-7 很好，< 1e-5 可接受，> 1e-3 有bug
    """
    params_values, keys = dictionary_to_vector(parameters)
    grad_values, _ = dictionary_to_vector(gradients)
    num_parameters = params_values.shape[0]
    
    gradapprox = np.zeros((num_parameters, 1))
    
    for i in range(num_parameters):
        # 计算 J(theta + epsilon)
        thetaplus

梯度检验的注意事项

只在调试时使用，不要在训练循环中——太慢了
如果使用Dropout，检验时要关闭它
检验时用几个训练样本即可，不需要全部数据
如果差异很大，逐个参数检查，找出哪个梯度计算错了

实践技巧总结

深度学习的实践是科学与艺术的结合。这一节的技巧看似繁杂，但都围绕一个核心目标：让模型在训练集和测试集上都表现良好，既要拟合数据，又要泛化到新数据。

诊断问题的流程：

看训练集误差：高则增大模型容量（更多层或神经元）
看验证集误差：比训练集高很多则加正则化或更多数据
看代价函数曲线：不下降检查学习率和梯度计算
持续迭代直到满意

在下一节，我们将学习更高级的优化算法——Momentum、RMSprop、Adam。标准梯度下降虽然简单，但在大规模问题上收敛太慢。这些改进的算法能将训练速度提升几倍甚至几十倍。