超参数调优与批归一化

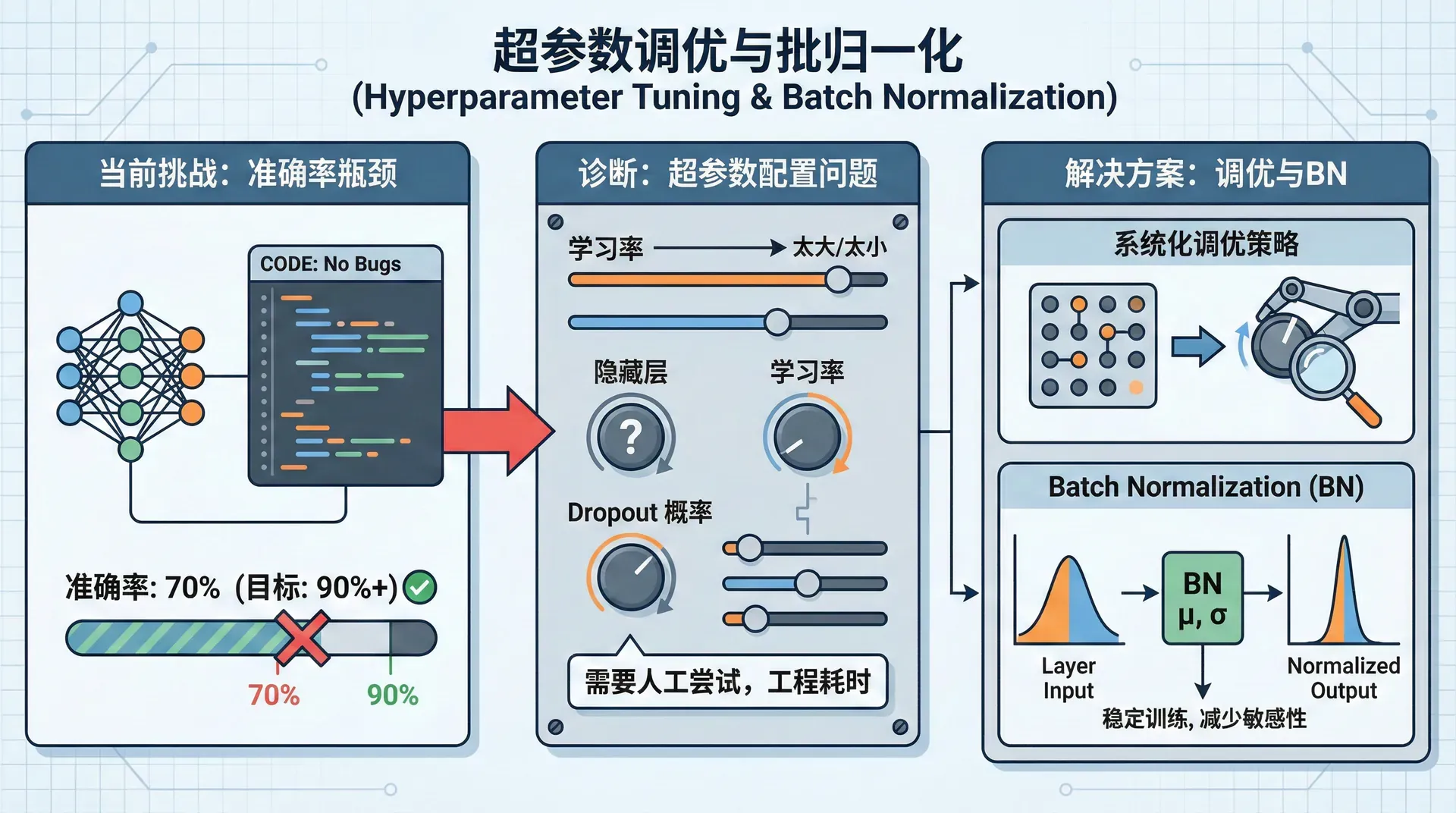
你精心设计了一个神经网络架构，实现了完美的前向传播和反向传播，代码没有bug。但训练出来的模型准确率只有70%，而你知道这个任务应该能达到90%以上。 问题出在哪？很可能是超参数没调好——学习率太大导致发散，或者太小导致困在局部最优；隐藏层太少导致欠拟合，或者Dropout概率不合适。

超参数调优是深度学习工程中最耗时的部分之一。不像参数可以通过梯度下降自动学习，超参数需要人工尝试。本节将介绍系统化的调优策略，以及Batch Normalization这个让训练更稳定、减少超参数敏感性的重要技术。

超参数的重要性排序

深度学习模型有很多超参数,但它们的重要性差异巨大。理解这个优先级能让你的调参更高效。

最重要（必须调）：

• 学习率 $\alpha$：影响最大。太大发散，太小收敛慢或困在局部最优

较重要（通常需要调）：

• Mini-batch大小：影响训练速度和稳定性，通常64-512
• 隐藏层神经元数：影响模型容量
• Momentum的 $\beta$ (如0.9)：使用Momentum或Adam时

次要（用默认值通常就行）：

• 网络层数：通常从2-3层开始，不够再加
• 学习率衰减：有帮助但不是必需
• Adam的 $\beta_1, \beta_2, \epsilon$：默认值0.9, 0.999, 1e-8通常很好

实践策略：先调学习率，找到一个合理范围；再调batch size和网络大小；最后微调其他参数。

随机搜索 vs 网格搜索

假设你要调两个超参数：学习率和隐藏层大小。网格搜索是这样做的：

|
for lr in [0.001, 0.01, 0.1]:
    for hidden_size in [50, 100, 200]:
        # 训练模型，评估性能

这会尝试3×3=9种组合。看起来系统化，但有个致命问题：如果学习率很重要而hidden_size不重要，你实际上只尝试了3个不同的学习率值。大部分计算资源浪费在了不重要的参数上。

随机搜索更好：在超参数空间中随机采样，尝试同样多的组合，但探索了更多不同的学习率值：

|
for trial in range(9):
    lr = 10 ** np.random.uniform(-4, -1)  # 0.0001到0.1
    hidden_size = np.random.randint(50, 200)
    # 训练模型

随机搜索让你更可能找到重要参数的最优值。2012年Bergstra和Bengio的论文证明，随机搜索在实践中几乎总是优于网格搜索。

合适的采样尺度

不是所有超参数都应该均匀采样。学习率就是个好例子。

错误做法（均匀采样）：

|
lr = np.random.uniform(0.0001, 1)  # 90%的值会在0.1到1之间

这样采样，大部分值会落在0.1-1之间，但经验告诉我们学习率通常在0.0001-0.01之间。我们需要在对数尺度上均匀采样：

正确做法（对数尺度）：

|
log_lr = np.random.uniform(-4, 0)  # -4到0之间均匀
lr = 10 ** log_lr  # 0.0001到1之间对数均匀

这样0.0001-0.001, 0.001-0.01, 0.01-0.1, 0.1-1各有25%的概率。

为什么要对数尺度？ 因为学习率的效果是乘性的。从0.001到0.01提升10倍，从0.1到1也提升10倍，虽然绝对差异不同，但对训练的影响是相似的。

类似地，正则化参数 $\lambda$、Adam的 $\beta$ 参数（$1-\beta$）也应该对数尺度采样。

|
# 采样beta（如0.9到0.999）
# 采样1-beta，因为它更接近线性影响
log_1_minus_beta = np.random.uniform(-3, -1)  # 0.001到0.1
beta = 1 - 10 ** log_1_minus_beta  # 0.9到0.999

调参策略：Pandas vs Caviar

有两种调参哲学，类比为养熊猫和养鱼：

Pandas方法（Babysitting one model）：

• 你只有一个GPU，或者数据集巨大训练很慢
• 训练一个模型，每天观察学习曲线，手动调整超参数
• 像养熊猫一样精心照料一个模型

Caviar方法（Training many models in parallel）：

• 你有多个GPU或TPU
• 同时训练很多模型（不同超参数组合），最后选最好的
• 像鱼产卵一样，数量取胜

大公司（如Google、Facebook）通常用Caviar方法——资源充足时，并行尝试比顺序尝试更快。但如果资源有限，Pandas方法可能更现实。

无论哪种方法，都要系统化记录：哪些超参数尝试过，效果如何，用Excel或专门的实验管理工具（如Weights & Biases、MLflow）跟踪。

Batch Normalizatio

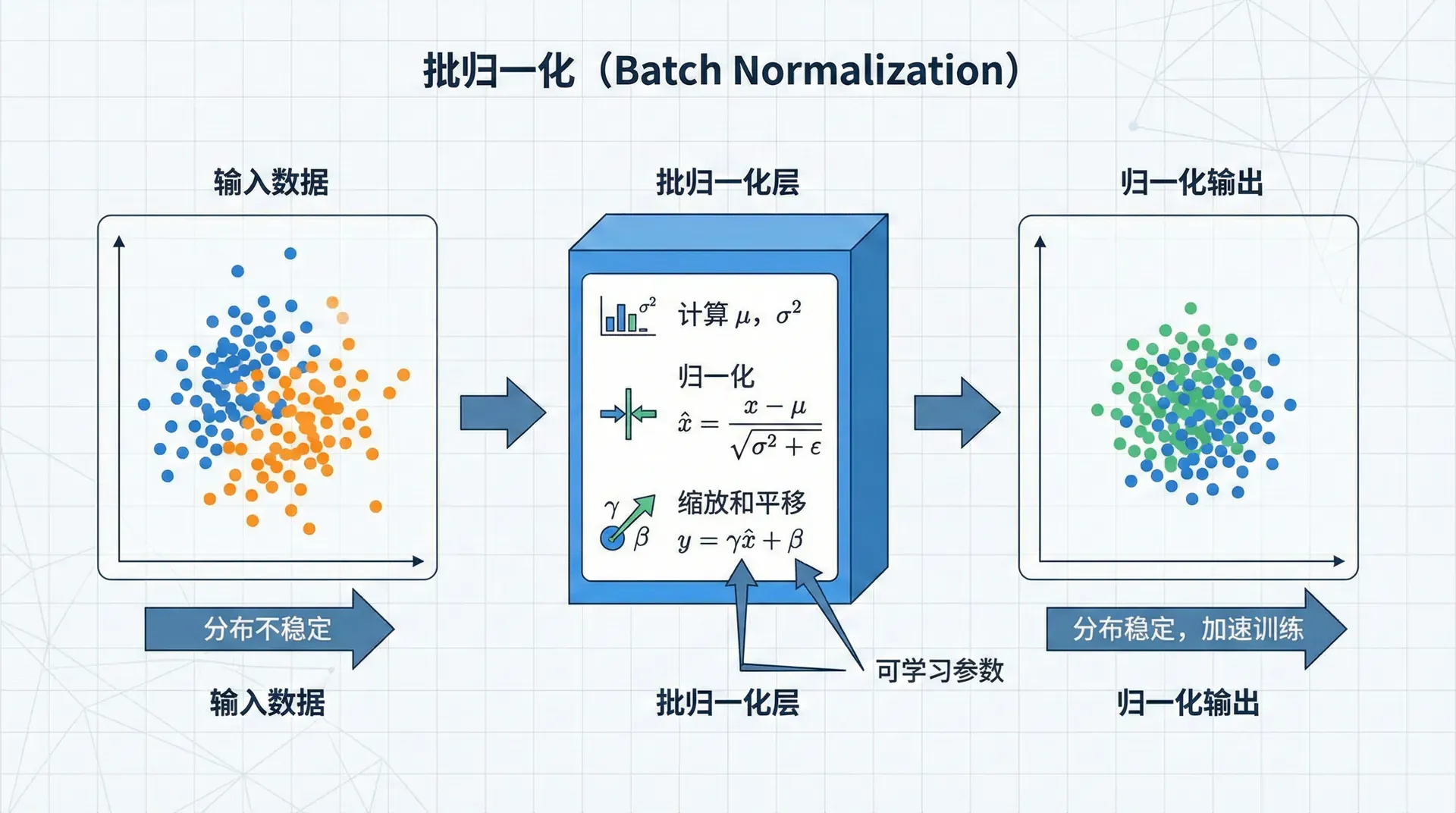
Batch Normalization（批归一化，简称BN）是2015年Ioffe和Szegedy提出的技术，极大地改善了深度网络的训练。它的核心思想简单但强大：归一化每一层的输入。

我们知道归一化输入能加速训练。BN将这个思想应用到网络的每一层：不仅归一化输入 $X$，还归一化隐藏层的激活值 $A^{[l]}$。

BN的数学原理

对于某一层的激活值 $Z^{[l]}$（或者 $A^{[l]}$，在激活函数之前或之后都可以），BN做以下变换：

这里 $\mu$ 和 $\sigma^2$ 是该mini-batch的均值和方差，$\epsilon$（如$10^{-8}$）防止除零。关键是最后一步：引入可学习的参数 $\gamma$ 和 $$。

为什么需要 $\gamma$ 和 $\beta$？ 简单归一化会限制网络的表达能力。比如sigmoid激活函数在0附近接近线性，归一化后所有值都在0附近，丢失了非线性。$\gamma$ 和 $\beta$ 让网络能够"撤销"归一化——如果网络学到 $\gamma = \sqrt{\sigma^2}$ 和 ，就恢复了原始值。

BN的效果

1. 允许更大的学习率：归一化后梯度更稳定，不容易爆炸或消失
2. 减少对初始化的敏感性：权重初始化不够好也能训练
3. 正则化效果：每个mini-batch的均值/方差有随机性，类似Dropout
4. 加速收敛：实践中常能将训练速度提升2-3倍

|
def batch_norm_forward(Z, gamma, beta, epsilon=1e-8):
    """
    Batch Normalization前向传播（训练时）
    Z: shape (n, m) - 一层的激活值
    gamma, beta: shape (n, 1) - 可学习参数
    """
    # 计算均值和方差（跨样本维度）
    mu = np.mean(Z, axis=1, keepdims=True)
    sigma2 = np.var(Z, axis=1, keepdims=True)
    
    # 归一化
    Z_norm =

测试时的BN

训练时，BN使用当前mini-batch的统计量。但测试时，我们可能一次只预测一个样本，没有"batch"。解决方案是：在训练过程中维护均值和方差的指数加权平均，测试时使用这些平均值。

|
# 训练时维护running averages
running_mean = beta * running_mean + (1-beta) * mu_batch
running_var = beta * running_var + (1-beta) * sigma2_batch
 
# 测试时
Z_norm_test = (Z_test - running_mean) / np.sqrt(running_var + epsilon)
Z_tilde_test = gamma * Z_norm_test +

Softmax回归：多分类问题

前面我们一直在处理二分类（是或否）。但很多问题是多分类：识别10个数字、分类1000种物体等。Softmax回归是逻辑回归在多分类上的推广。

输出层有 $K$ 个神经元（$K$ 个类别），每个输出 $z^{[L]}_k$。Softmax函数将这些值转换为概率分布：

每个 $a^{[L]}_k \in (0, 1)$ 且 $\sum_{k=1}^K a^{[L]}_k = 1$，可以解释为属于第 类的概率。

损失函数是交叉熵的多分类版本：

这里 $y$ 是one-hot编码：如果样本属于第2类，$y = [0, 1, 0, ..., 0]$。

反向传播的梯度形式优雅：

与二分类完全一样的形式！

|
def softmax(Z):
    """
    Softmax激活函数
    Z: shape (K, m) - K个类别，m个样本
    """
    # 减去最大值防止数值溢出
    Z_exp = np.exp(Z - np.max(Z, axis=0, keepdims=True))
    return Z_exp / np.sum(Z_exp, axis=0, keepdims=True)
 
# 使用示例：10分类问题
Z_last = np.dot(W_last, A_prev) + b_last  

深度学习框架选择

到目前为止，我们从零实现了所有算法。这对理解原理很重要，但实际项目中，使用成熟的深度学习框架能节省大量时间。

主流框架（2026年）：

1. PyTorch：最流行的研究框架，动态计算图，易于调试
2. TensorFlow/Keras：Google出品，工业部署生态好
3. JAX：Google新框架，强调函数式编程和自动微分

选择标准：

• 研究/原型：PyTorch，灵活性最好
• 生产部署：TensorFlow Serving或PyTorch TorchServe
• 需要XLA加速：JAX或TensorFlow
• 移动端：TensorFlow Lite或PyTorch Mobile

框架虽然重要，但更重要的是理解深度学习的原理。框架API会变，但反向传播、正则化这些核心概念不变。掌握了原理，切换框架只需几天学习曲线。

从基础到实践的跨越

到此为止，我们已经掌握了训练神经网络的所有核心技术：前向传播、反向传播、各种优化算法、正则化、超参数调优。但还有一个维度我们没深入讨论：如何系统化地改进一个模型？如何诊断问题并有针对性地优化？

在下一节，我们将学习机器学习策略——不是新的算法或技术，而是一套思维框架，帮助你高效地迭代改进模型，避免在错误的方向上浪费时间。这些策略来自Andrew Ng等人多年的项目经验总结，是深度学习工程化的精髓。