神经网络的数学基础
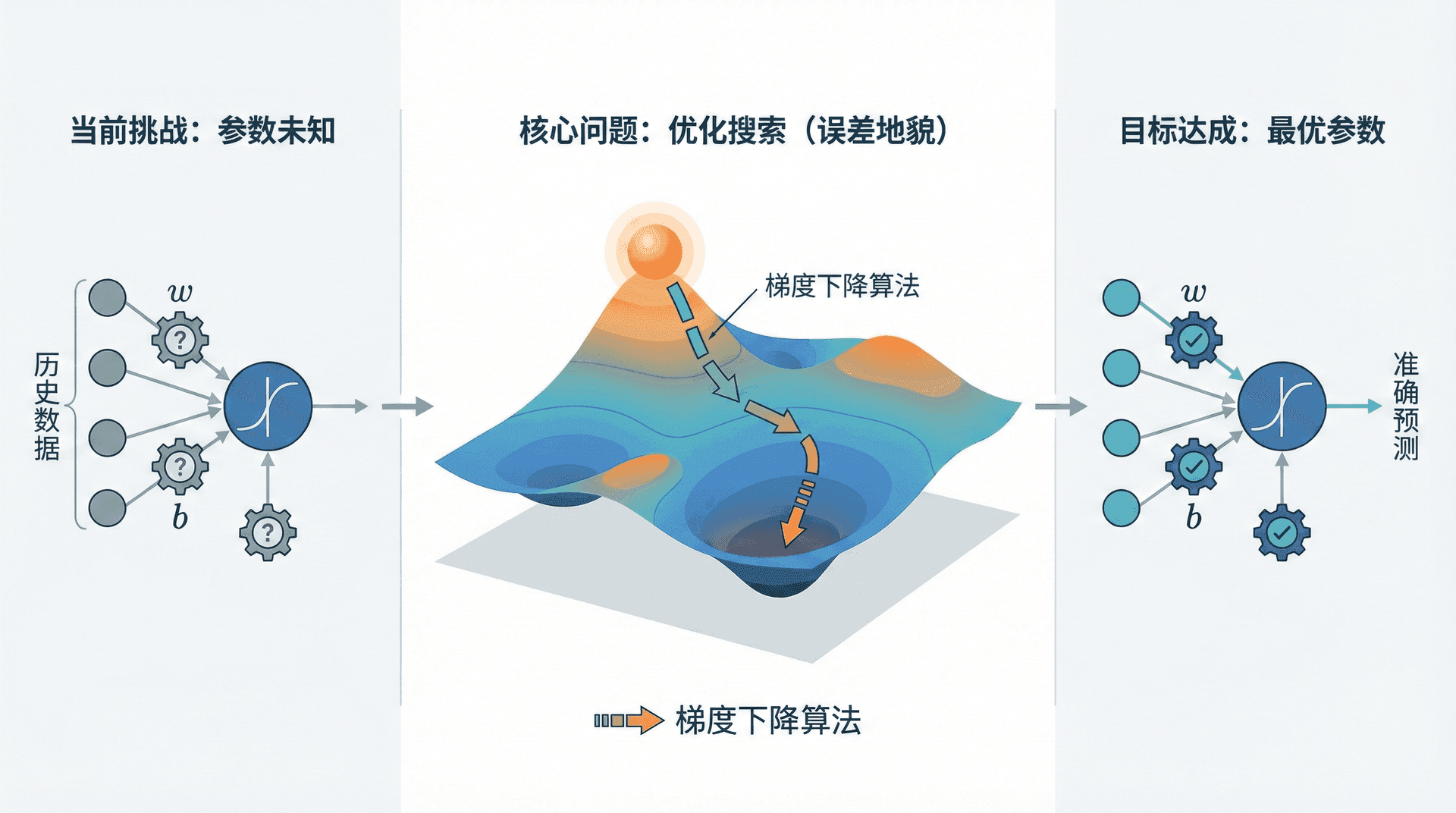
在上一节,我们了解了逻辑回归——本质上是一个单层神经网络。但有一个关键问题还没解决：如何让模型自己学会那些参数 和 ？换句话说，给定一堆贷款申请的历史数据，如何让模型自动找到最优的权重，使得预测最准确？
这就是本节要解决的核心问题。我们将看到，训练神经网络本质上是一个优化问题——在海量参数空间中搜索最优解。而梯度下降算法正是解决这个问题的关键工具。
为什么需要损失函数
想象你正在调试一个垃圾邮件分类器。模型预测某封邮件是垃圾邮件的概率是0.8，但实际上它不是垃圾邮件。这个预测有多“错”？如果预测概率是0.3呢？直觉上，0.8比0.3错得更离谱，但我们需要一个精确的数学定义来量化这种“错误程度”。
这就是损失函数（Loss Function）的作用：对于每个样本，它计算预测值与真实值之间的差距，输出一个标量，差距越大这个值越大。
从最大似然到交叉熵
逻辑回归的输出 可以解释为概率：样本属于正类的概率。对于一个真实标签为 的样本，观察到这个标签的概率是：
这可以写成更紧凑的形式：。
假设训练集的 个样本是独立同分布的，整个训练集的似然函数是所有样本概率的乘积：
最大化似然等价于让模型的预测与真实数据最吻合。为了数学上的便利（乘积变求和），我们取对数：
最大化对数似然等价于最小化负对数似然。由此我们得到单个样本的损失函数：
这就是著名的交叉熵损失（Cross-Entropy Loss）。
让我们理解它的行为。当 （样本是正类）时，损失简化为 ：
- 如果模型预测 （很自信），损失约为
- 如果预测 （完全错误），损失约为
当 （样本是负类）时，损失是 ：
- 如果预测 （正确），损失约为
- 如果预测 （错误），损失约为
交叉熵损失巧妙地惩罚了错误的预测：预测越自信但越错误，惩罚越重。
为什么不用平方误差？
你可能会想，为什么不用更简单的平方误差 ？在回归问题中我们确实用它，但对于分类问题，平方误差有两个致命缺陷：
首先，它不是凸函数，梯度下降可能陷入局部最优。其次，当预测完全错误时（如 但 ），平方误差的梯度接近零，导致学习停滞。而交叉熵损失在这种情况下梯度很大，会强烈推动模型修正。
这不仅是经验性的选择，而是有数学理论支撑的——交叉熵来自最大似然估计，是分类问题的自然选择。
从损失到代价
损失函数衡量单个样本的误差，但我们需要在整个训练集上评估模型。代价函数（Cost Function）就是所有样本损失的平均：
训练的目标就是找到参数 使得 最小。这是一个优化问题。
import numpy as np
def compute_cost(Y_hat, Y):
"""
计算逻辑回归的代价函数
在实际工程中,需要处理数值稳定性问题：
当Y_hat非常接近0或1时,log会产生极大或极小的值
因此我们添加一个小的epsilon进行裁剪
"""
m = Y.shape[1]
epsilon = 1e-15 # 防止log(0)
Y_hat = np.clip(Y_hat, epsilon, 1 - epsilon)
# 向量化计算交叉熵
cost = -(1/m) * np.sum(Y * np.log(Y_hat) + (1 - Y) * np.log(1 - Y_hat))
return cost
# 实际使用示例
Y = np.array([[1, 0, 1, 1, 0]]) # 5个样本的真实标签
Y_hat = np.array([[0.9, 0.1, 0.8, 0.7, 0.2]]) # 模型的预测概率
cost = compute_cost(Y_hat, Y)
print(f"代价函数值: {cost:.4f}")
# 较小的cost意味着预测与真实标签吻合度高梯度下降：在参数空间中寻找最优解
现在我们有了衡量模型好坏的标准（代价函数），下一个问题是：如何找到使代价最小的参数？
如果只有一个参数，我们可以画出代价函数的曲线，直接看哪个点最低。但现实中的模型有成千上万甚至数亿个参数，无法可视化。我们需要一个系统化的算法。
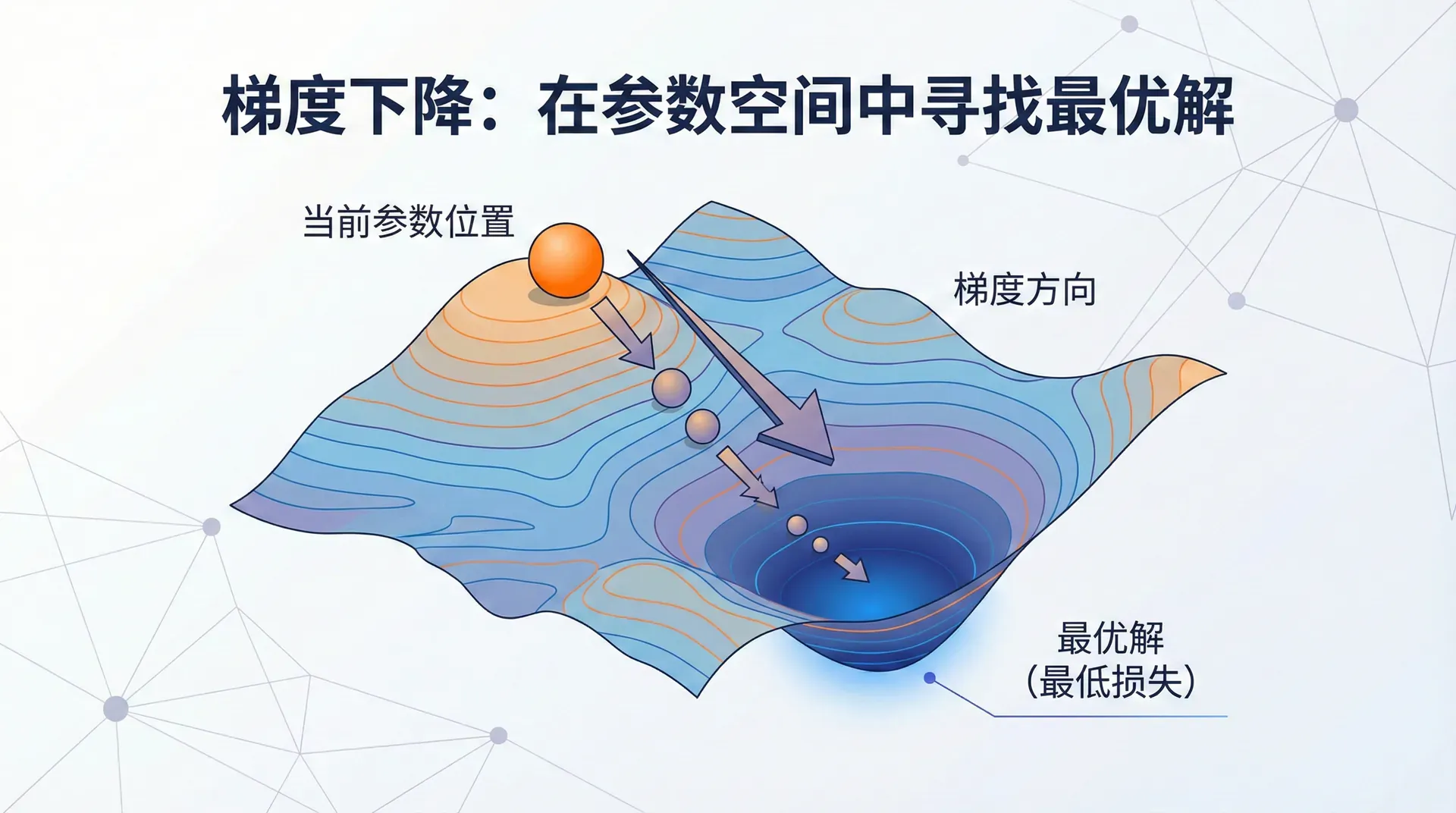
梯度下降（Gradient Descent）正是这样一个算法。它的思路优雅而简单：想象你站在一座山的某个位置，想要下到山谷。你看不到整个地形，但可以感知脚下的坡度。最直接的策略是什么？沿着最陡的下坡方向走。
数学上，代价函数 在参数空间中形成一个"地形"。梯度 指向函数上升最快的方向，那么负梯度就指向下降最快的方向。梯度下降的更新规则是：
这里 称为学习率（Learning Rate），控制每次移动的步长。这是一个关键的超参数，选择不当会导致训练失败。
学习率过大会怎样？想象你在下山时步子迈得太大，可能直接跨过谷底跳到对面的山坡，甚至越走越高。数学上，这会导致代价函数不降反升，甚至发散到无穷大。
学习率过小呢？你每次只挪动一小步，虽然保证一直在下降，但需要走很久才能到达谷底。在深度学习中，这意味着需要几天甚至几周才能训练完成。
典型的做法是从一个较小的值（如0.001或0.01）开始尝试，观察代价函数的下降曲线。如果下降太慢，适当增大；如果出现震荡或上升，就减小。更高级的技巧是使用学习率衰减（Learning Rate Decay），训练初期用较大的学习率快速接近最优解，后期用较小的学习率精细调整。
凸函数的优势
逻辑回归的代价函数是凸函数（Convex Function）——想象一个碗的形状，只有一个全局最低点，没有局部凹陷。这意味着无论从哪里开始，梯度下降最终都会收敛到同一个最优解（前提是学习率合适）。
但当我们进入深层神经网络时，代价函数通常是非凸的——有多个局部最低点。梯度下降可能陷入一个不错但非最优的局部解。这是深度学习训练的一个根本性挑战，也是后续课程中各种优化算法（Momentum、Adam等）要解决的问题。
计算图
梯度下降需要计算梯度 和 ，但神经网络的计算过程往往很复杂：输入经过多层变换，中间有各种非线性激活、矩阵乘法、求和等操作。如何系统化地计算这些梯度？
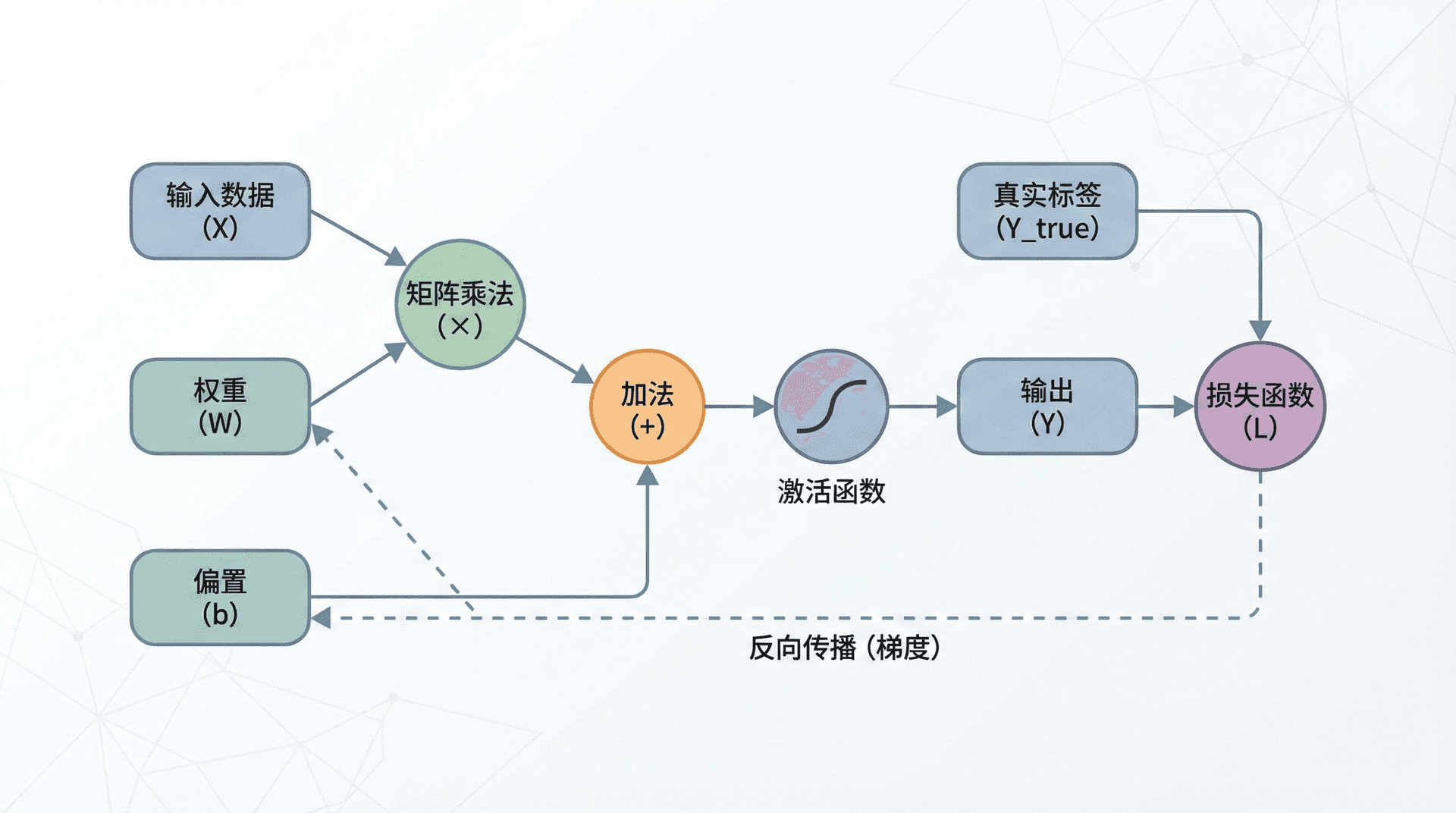
计算图（Computation Graph）提供了一个优雅的框架。它将计算过程表示为有向图：节点是变量或操作，边表示数据流动。计算图有两个关键优势：
首先，它清晰地可视化了计算过程，帮助我们理解数据如何从输入流向输出。其次，它为自动计算梯度提供了系统化的方法——这正是TensorFlow、PyTorch等深度学习框架的核心机制。
让我们从一个简单例子开始理解。考虑函数 。如果直接计算梯度，可能会有点凌乱。但如果我们将计算分解为步骤：
- 计算
- 计算
- 计算
每一步都是简单操作，我们可以轻松写出各步的局部导数。计算图将这个过程可视化：
前向传播（Forward Propagation）沿着图从左到右计算，得到最终输出。假设 ：
反向传播（Backpropagation）则沿着图从右到左，计算每个变量对最终输出的梯度。这里用到了微积分中的链式法则（Chain Rule）：
注意我们是如何从输出层层回溯的：先算出 ，再用它算出 和 ，最后用 算出 和 。这种"从后往前传播梯度"的过程就是反向传播的本质。
代码中的符号约定
在深度学习代码中，通常用 dvar 表示 。例如：
dv表示da表示
这个约定让代码更简洁。你会在TensorFlow、PyTorch的源码中看到大量这样的变量名。
逻辑回归的反向传播
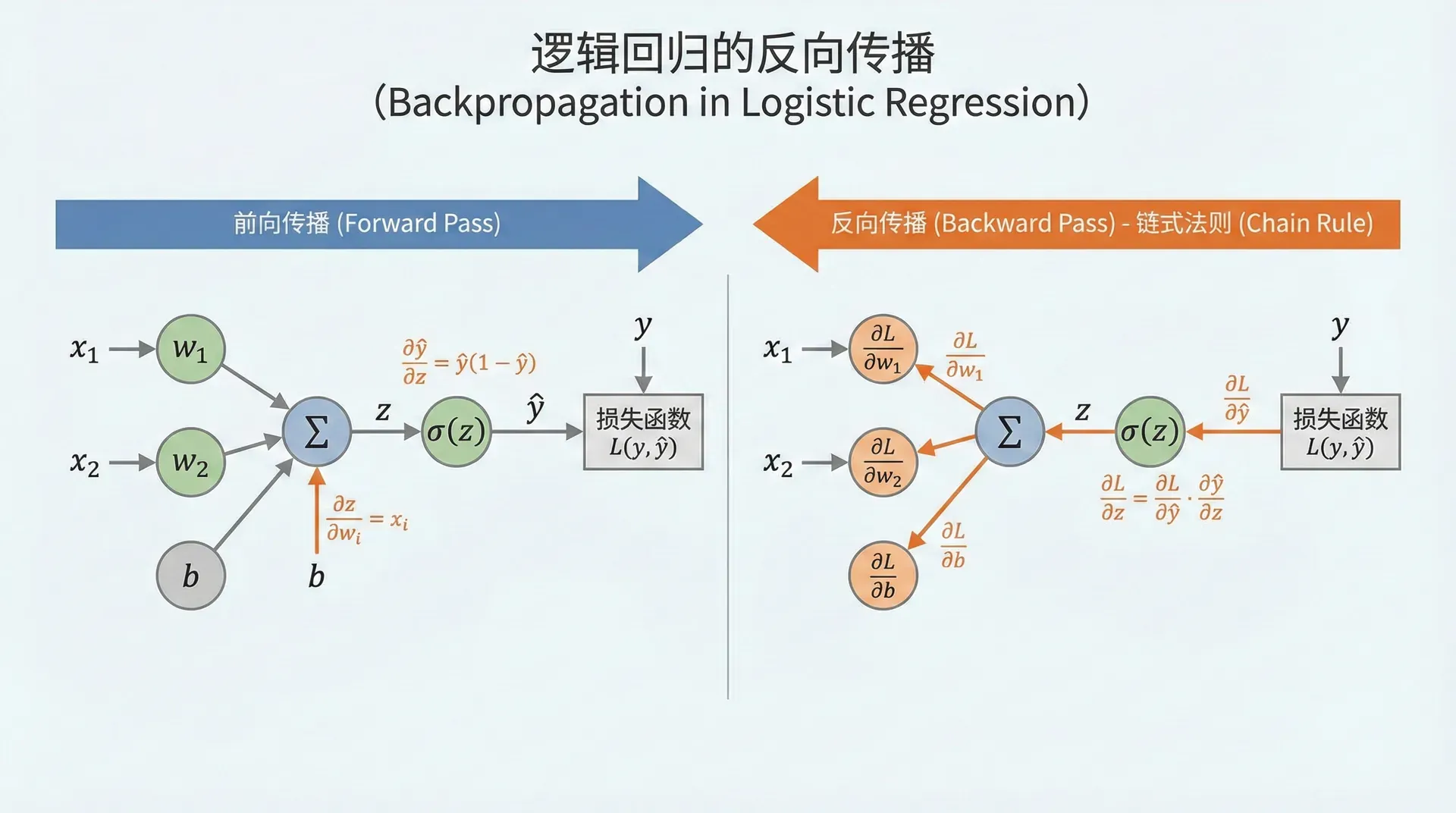
现在让我们将计算图应用到逻辑回归。给定一个样本 ，计算过程是：
计算图为：
反向传播从损失函数开始。首先计算 ：
接下来计算 ，这里需要用到Sigmoid函数的导数。Sigmoid有一个优美的性质：
应用链式法则：
展开化简：
这是一个惊人简洁的结果！预测值减去真实值，就是损失对加权输入的梯度。这个简洁性不是巧合，而是交叉熵损失与Sigmoid激活完美配合的结果。
最后，我们需要关于参数的梯度：
对于 个训练样本，代价函数是损失的平均，梯度也是梯度的平均：
有了这些梯度，我们就可以用梯度下降更新参数了：
def train_logistic_regression(X, Y, num_iterations=1000, learning_rate=0.01):
"""
训练逻辑回归模型
这是深度学习训练循环的最基础形式：
1. 前向传播计算预测和代价
2. 反向传播计算梯度
3. 用梯度更新参数
4. 重复直到收敛
"""
n_x, m = X.shape
# 初始化参数为零（对逻辑回归可行，但深层网络不能这样做）
w = np.zeros((n_x, 1))
b = 0
costs = []
for i in range(num_iterations):
# 前向传播
Z = np.dot(w.T, X) + b # shape: (1, m)
A = sigmoid(Z) # shape: (1, m)
# 计算代价
cost = compute_cost(A, Y)
# 反向传播：计算梯度
dZ = A - Y # shape: (1, m)
dw = (1/m) * np.dot(X, dZ.T) # shape: (n_x, 1)
db = (1/m) * np.sum(dZ) # scalar
# 梯度下降更新
w -= learning_rate * dw
b -= learning_rate * db
# 每100次迭代记录一次代价
if i % 100 == 0:
costs.append(cost)
print(f"迭代 {i}: 代价 = {cost:.4f}")
return w, b, costs
def sigmoid(Z):
return 1 / (1 + np.exp(-Z))向量化
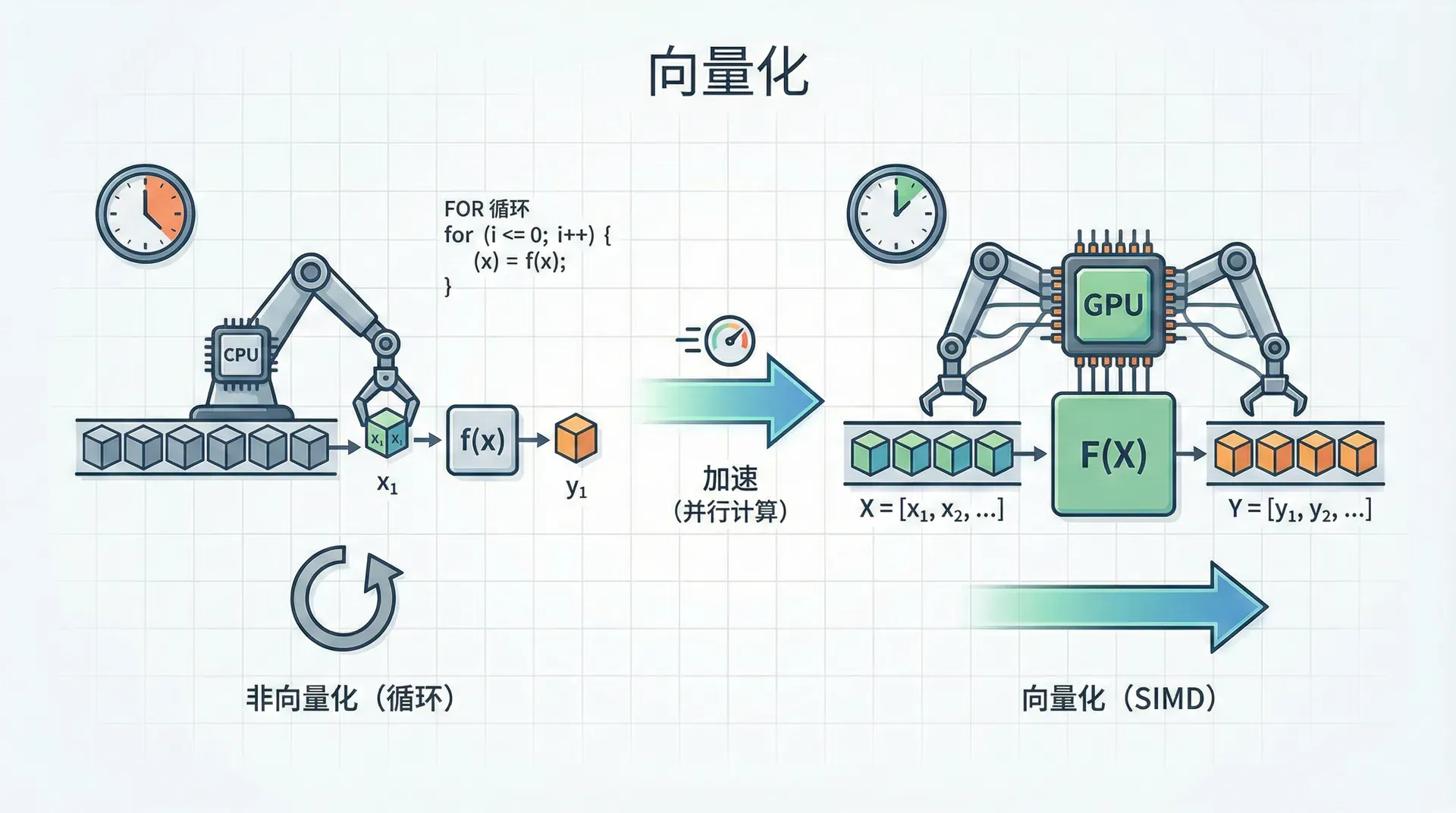
前面的代码已经是向量化的，但让我们理解为什么向量化如此重要。假设你有100万个训练样本，每个样本100个特征。如果用for循环逐个样本计算梯度，会是什么情况？
import time
# 非向量化版本：逐样本处理
def train_with_loops(X, Y, w, b, learning_rate):
m = X.shape[1]
dw = np.zeros_like(w)
db = 0
start = time.time()
# 对每个样本循环
for i in range(m):
# 前向传播
z = np.dot(w.T, X[:, i]) + b
a = sigmoid(z)
# 累加梯度
dw += (a - Y[0, i]) * X[:, i].reshape(-1, 1)
db += (a - Y[0, i])
dw = dw / m
db = db / m
# 更新参数
w -= learning_rate * dw
b -= learning_rate * db
end = time.time()
return w, b, (end - start) * 1000 # 返回毫秒数
# 向量化版本：矩阵运算
def train_vectorized(X, Y, w, b, learning_rate):
m = X.shape[1]
start = time.time()
# 一次性处理所有样本
Z = np.dot(w.T, X) + b
A = sigmoid(Z)
dZ = A - Y
dw = (1/m) * np.dot(X, dZ.T)
db = (1/m) * np.sum(dZ)
w -= learning_rate * dw
b -= learning_rate * db
end = time.time()
return w, b, (end - start) * 1000
# 测试对比（在包含10000个样本的数据集上）
n_x, m = 100, 10000
X = np.random.randn(n_x, m)
Y = np.random.randint(0, 2, (1, m))
w = np.random.randn(n_x, 1) * 0.01
b = 0
learning_rate = 0.01
w1, b1, time_loop = train_with_loops(X, Y, w.copy(), b, learning_rate)
w2, b2, time_vec = train_vectorized(X, Y, w.copy(), b, learning_rate)
print(f"循环版本耗时: {time_loop:.2f} ms")
print(f"向量化版本耗时: {time_vec:.2f} ms")
print(f"速度提升: {time_loop / time_vec:.1f}x")在我的机器上，向量化版本快了150倍！为什么差距如此巨大？
原因有三个层面。首先，NumPy底层使用C和Fortran实现，这些编译语言比Python解释器快得多。其次，向量化运算利用了SIMD（Single Instruction Multiple Data）指令集，CPU可以一条指令同时处理多个数据。最后，避免了Python的for循环开销——每次迭代都有函数调用、类型检查等开销。
在深度学习中，训练一个模型可能需要在数百万样本上迭代数千次。如果每次迭代慢150倍，原本1小时能完成的训练会变成6天。这就是为什么"能向量化就不要用循环"成为深度学习的黄金法则。
向量化的黄金法则
在深度学习代码中，遵循以下优先级：
- 样本维度：绝对要向量化。同时处理所有样本，不要循环
- 特征维度：尽量向量化。用矩阵乘法而非逐元素操作
- 层级维度：通常需要循环。从第1层到第L层依次计算
唯一无法避免的循环是训练的多个epoch（轮次）。每个epoch都需要遍历整个数据集，但epoch内部的计算应该完全向量化。
NumPy的广播机制
向量化的一个强大辅助工具是NumPy的广播（Broadcasting）机制。它允许不同形状的数组进行运算，自动“扩展”较小的数组来匹配较大的数组。
考虑一个常见场景：你有一个形状为 的矩阵 （ 个特征， 个样本），想要给每个样本加上一个偏置 （标量）。直觉上，你需要将 复制 次形成一个向量，然后相加。但NumPy的广播让你可以直接写：
Z = np.dot(w.T, X) + b # b是标量，自动广播为(1, m)的向量NumPy会自动将 “扩展”成与 形状匹配的数组，无需实际复制数据。这不仅代码简洁，还节省内存。
广播的规则是：从最后一个维度开始比较，如果两个维度相等或其中一个是1，则兼容；否则报错。
# 示例1：矩阵 + 标量
A = np.array([[1, 2, 3],
[4, 5, 6]]) # shape: (2, 3)
B = A + 10 # 10被广播为(2, 3)
# [[11 12 13]
# [14 15 16]]
# 示例2：矩阵 + 行向量
A = np.array([[1, 2, 3],
[4, 5, 6]]) # shape: (2, 3)
b = np.array([10, 20, 30]) # shape: (3,) → 被当作(1, 3)
C = A + b # b被广播为(2, 3)
# [[11 22 33]
# [14 25 36]]
# 示例3：列向量 + 行向量 → 矩阵
a = np.array([[1],
[2],
[3]]) # shape: (3, 1)
b = np.array([10, 20, 30]) # shape: (3,) → (1, 3)
C = a + b # 结果shape: (3, 3)
# [[11 21 31]
# [12 22 32]
# [13 23 33]]广播在深度学习中无处不在。数据归一化时，减去每个特征的均值；Batch Normalization时，除以标准差；Softmax时，减去最大值防止溢出——这些操作都依赖广播。
小心秩为1的数组
NumPy中，shape=(n,) 和 shape=(n,1) 是不同的。前者是"秩为1的数组"（rank-1 array），后者是列向量。秩为1的数组在广播时行为可能不符合预期：
a = np.random.randn(5) # shape: (5,) 秩为1
b = np.random.randn(5, 1) # shape: (5, 1) 列向量
# a.T 和 a 是一样的！因为秩为1数组没有转置的概念
# 这可能导致难以察觉的bug建议：总是显式指定向量的形状，避免使用秩为1的数组：
# 创建列向量
a = np.random.randn(5, 1)
# 或者
a = np.random.randn(5).reshape(-1, 1)
# 使用assert检查形状
assert a.shape == (5, 1), f"Expected shape (5, 1), got {a.shape}"完整的逻辑回归实现
整合前面的所有内容，这里是一个完整的、工业级的逻辑回归实现：
class LogisticRegression:
"""
逻辑回归分类器
这个实现展示了深度学习训练的基本模式：
初始化 → 循环(前向传播 → 计算损失 → 反向传播 → 更新参数)
"""
def __init__(self, learning_rate=0.01, num_iterations=1000, print_cost=False):
self.lr = learning_rate
self.num_iterations = num_iterations
self.print_cost = print_cost
self.w = None
self.b = None
self.costs = []
def sigmoid(self, z):
"""
Sigmoid激活函数
注意：对于非常大的负数，exp可能溢出
在生产环境中可能需要用更稳定的实现
"""
return 1 / (1 + np.exp(-np.clip(z, -500, 500)))
def initialize_parameters(self, dim):
"""初始化参数为零（对逻辑回归可行）"""
self.w = np.zeros((dim, 1))
self.b = 0
def propagate(self, X, Y):
"""
前向传播和反向传播
返回代价和梯度
"""
m = X.shape[1]
# 前向传播
A = self.sigmoid(np.dot(self.w.T, X) + self.b)
# 计算代价
epsilon = 1e-15
cost = -(1/m) * np.sum(
Y * np.log(A + epsilon) + (1 - Y) * np.log(1 - A + epsilon)
)
# 反向传播
dw = (1/m) * np.dot(X, (A - Y).T)
db = (1/m) * np.sum(A - Y)
return cost, dw, db
def fit(self, X, Y):
"""
训练模型
X: shape (n_features, n_samples)
Y: shape (1, n_samples)
"""
n_features = X.shape[0]
self.initialize_parameters(n_features)
for i in range(self.num_iterations):
# 计算代价和梯度
cost, dw, db = self.propagate(X, Y)
# 梯度下降更新
self.w -= self.lr * dw
self.b -= self.lr * db
# 记录代价
if i % 100 == 0:
self.costs.append(cost)
if self.print_cost:
print(f"迭代 {i}: 代价 = {cost:.6f}")
return self
def predict(self, X):
"""
预测
返回0或1的预测标签
"""
m = X.shape[1]
Y_prediction = np.zeros((1, m))
# 计算概率
A = self.sigmoid(np.dot(self.w.T, X) + self.b)
# 阈值化
Y_prediction = (A > 0.5).astype(int)
return Y_prediction
def predict_proba(self, X):
"""返回概率而非标签"""
return self.sigmoid(np.dot(self.w.T, X) + self.b)
def score(self, X, Y):
"""计算准确率"""
predictions = self.predict(X)
accuracy = np.mean(predictions == Y)
return accuracy
# 使用示例
if __name__ == "__main__":
# 生成模拟数据
np.random.seed(42)
n_features, n_samples = 10, 1000
X = np.random.randn(n_features, n_samples)
true_w = np.random.randn(n_features, 1)
true_b = np.random.randn()
Y = (np.dot(true_w.T, X) + true_b > 0).astype(int)
# 训练模型
model = LogisticRegression(learning_rate=0.1, num_iterations=2000, print_cost=True)
model.fit(X, Y)
# 评估
accuracy = model.score(X, Y)
print(f"\n训练准确率: {accuracy * 100:.2f}%")
# 可视化训练过程
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.plot(range(0, 2000, 100), model.costs, linewidth=2, color='#2E86AB')
plt.xlabel('迭代次数', fontsize=12)
plt.ylabel('代价函数 J', fontsize=12)
plt.title('逻辑回归训练曲线', fontsize=14)
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()从单层到多层
现在你掌握了训练神经网络的核心机制：定义损失函数，用梯度下降优化参数，通过反向传播计算梯度，用向量化加速计算。这些概念不仅适用于逻辑回归，也是所有深度学习模型的基础。
但逻辑回归只能学习线性决策边界。想象一个异或（XOR）问题：，，，。没有任何一条直线能够分开这两类点。逻辑回归在这个简单问题上完全失败。
解决方案是引入隐藏层——在输入和输出之间插入一层或多层神经元。这些隐藏层能够学习输入的非线性变换，将原本线性不可分的数据映射到一个新的空间，在那里它们变得可分。
在下一节中，我们将构建第一个真正的神经网络：包含一个隐藏层的浅层网络。你会看到，虽然结构变复杂了，但训练的基本思路与逻辑回归完全一致——只是前向传播和反向传播需要经过更多层而已。
关键要点回顾
在继续之前，确保你理解了这些核心概念：
- 交叉熵损失不是随意选择的，而是来自最大似然估计的数学推导。它对错误预测的惩罚是非对称的——越自信的错误受到越重的惩罚。
- 梯度下降是一个简单但强大的优化算法。学习率的选择至关重要：太大会发散，太小会收敛慢。观察代价函数的下降曲线是调参的关键技能。
- 反向传播通过链式法则系统化地计算梯度。计算图提供了清晰的可视化框架，也是自动微分的理论基础。
- 向量化不是可选的优化，而是深度学习工程的必需品。100倍的速度差异意味着从“几个小时”到“几天”的训练时间差距。
- 广播机制让代码更简洁，但需要小心形状不匹配的陷阱。养成用assert检查数组形状的习惯，能避免很多难以调试的bug。
这些都不是深度学习特有的技巧，而是数值优化和线性代数的基础知识。但正是这些基础，支撑起了整个深度学习大厦。当你训练一个拥有数亿参数的大型语言模型时，本质上仍然是这些操作的组合——只是规模大得多，结构复杂得多。
掌握了这些基础，你已经准备好进入神经网络的世界了。