异常检测
在数据分析和机器学习中,我们常常需要识别“不正常”的数据点。信用卡公司需要检测欺诈交易,制造商需要发现有缺陷的产品,网络安全系统需要识别入侵行为,服务器监控系统需要发现异常的运行状态。这些都是异常检测(Anomaly Detection)的应用场景。
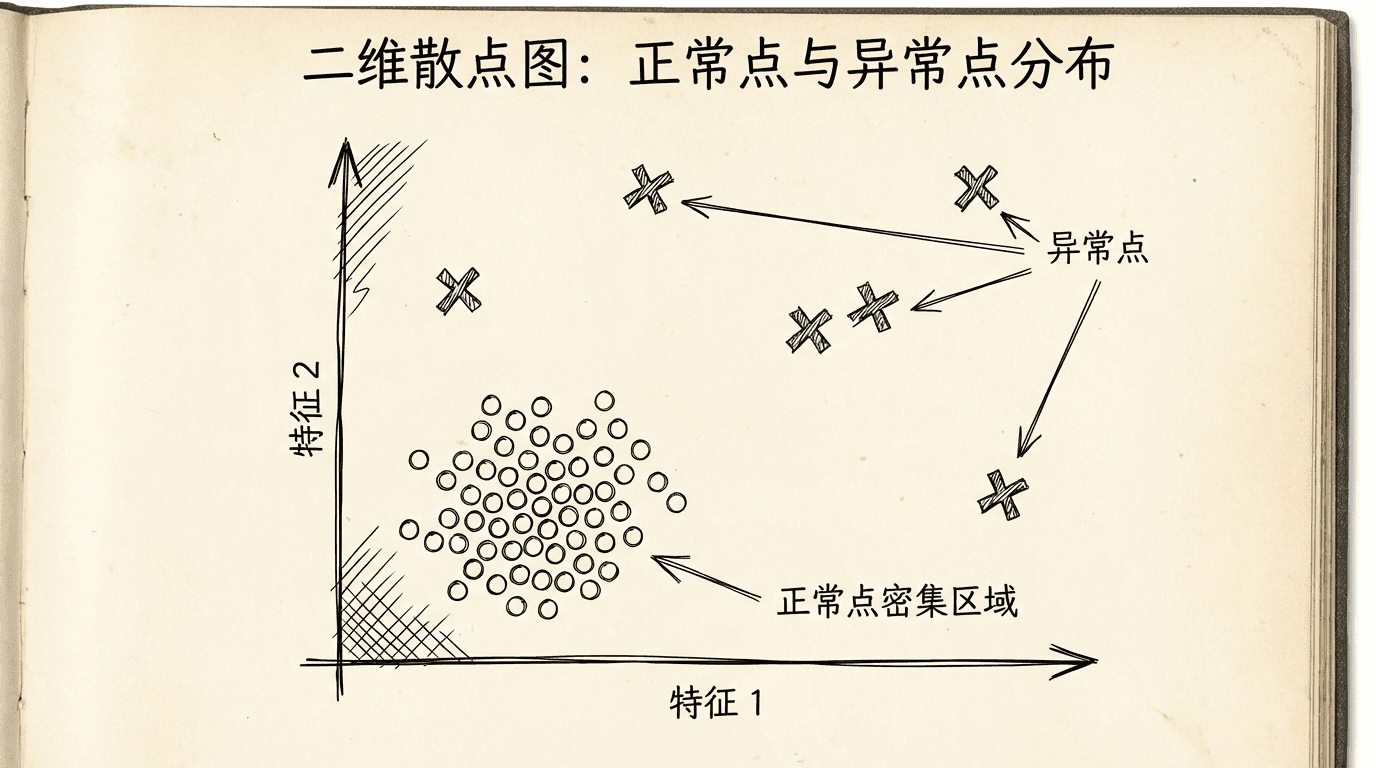
异常检测的核心思想是:大多数数据点都是“正常”的,遵循某种模式或分布;异常点则偏离这个正常模式。通过建立正常数据的模型,我们可以识别出那些不符合模型的异常点。
问题动机
如果你在运营一个数据中心,有数千台服务器。每台服务器有多个指标:CPU负载、内存使用、磁盘I/O、网络流量等。你想自动识别出行为异常的服务器——它们可能有硬件故障、软件问题或受到攻击。 人工监控成千上万台服务器是不可行的。但机器学习可以帮助我们:
- 用正常运行的服务器数据训练一个模型
- 模型学习正常行为的模式
- 当新的服务器数据到来时,计算它符合正常模式的程度
- 如果偏离程度超过阈值,标记为异常
异常检测的特点:
- 正常样本很多,异常样本很少
- 异常的类型多样,难以提前知道所有可能的异常模式
- 更像无监督学习而非监督学习
异常检测vs监督学习分类:虽然都是识别不同类型的数据,但异常检测适用于异常样本很少、异常类型多样的情况。如果有大量标记的异常样本,监督学习(如逻辑回归、SVM)可能更合适。
高斯分布
高斯分布(正态分布)是异常检测的数学基础。
单变量高斯分布:
如果 服从高斯分布,记为 ,其概率密度函数是:
其中:
- 是均值(分布的中心)
- 是方差(分布的宽度)
- 是标准差
参数估计:
给定数据集 ,估计参数:
|import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm # 生成高斯分布数据 mu, sigma = 0, 1 data = np.random.normal(mu, sigma, 1000) # 估计参数 mu_est = np.mean(data) sigma_est = np.std(data) # 画出数据分布和拟合的高斯曲线 plt.hist(data, bins=50, density
异常检测算法
基本思路:
- 对训练集(正常数据)的每个特征估计高斯分布参数
- 对于新样本,计算它在每个特征上的概率
- 综合所有特征的概率,判断样本是否异常
步骤1:选择特征
选择能够表征正常/异常行为的特征 。
|def fitGaussian(X): """ 拟合多元高斯分布(假设特征独立) X: 数据矩阵 (m x n) """ mu = np.mean(X, axis=0) sigma2 = np.var(X, axis=0) return mu, sigma2 def multivariateGaussian(X, mu, sigma2): """ 计算每个样本的概率密度 """ n = len(mu) sigma2 = sigma2.reshape(-
开发和评估异常检测系统
数据划分:
与监督学习不同,异常检测的数据划分有特殊之处:
- 训练集:只包含正常样本(或绝大多数是正常的)
- 验证集:包含正常样本和少量异常样本,用于选择阈值和特征
- 测试集:包含正常样本和少量异常样本,用于最终评估
例如:
- 训练集:6000个正常样本
- 验证集:2000个正常样本 + 10个异常样本
- 测试集:2000个正常样本 + 10个异常样本
评估指标:
不能用准确率(因为异常样本很少,总是预测为正常就能得到很高准确率)。应该用:
- 精确率(Precision)
- 召回率(Recall)
- F1分数
或者画出PR曲线(精确率-召回率曲线)。
特征选择:
选择能够区分正常和异常的特征很重要。画出每个特征的直方图,看是否符合高斯分布。如果不符合,可以尝试变换(如取对数)。
|# 检查特征分布 plt.figure(figsize=(12, 4)) for i in range(X_train.shape[1]): plt.subplot(1, X_train.shape[1], i+1) plt.hist(X_train[:, i], bins=50) plt.title(f'特征 {i+1}') plt.show() # 如果分布很偏,尝试对数变换
好的特征对于异常检测至关重要。如果现有特征不能区分正常和异常,考虑构造新特征。例如,在监控服务器时,可以构造“CPU使用率/网络流量”这样的组合特征,它在正常情况下可能是稳定的,异常时会有明显变化。
异常检测 vs 监督学习
何时使用异常检测,何时使用监督学习分类?
使用异常检测的情况:
- 异常样本非常少(比如0-20个),不足以训练监督学习模型
- 异常的类型多样,未来可能出现新类型的异常
- 例子:欺诈检测、制造业质检、数据中心监控
使用监督学习的情况:
- 正类和负类样本都比较多
- 正类(异常)的类型相对固定
- 例子:垃圾邮件分类、天气预报、疾病诊断
多变量高斯分布
前面我们假设各个特征独立,这简化了计算但可能不够准确。多变量高斯分布能够建模特征之间的相关性。
多变量高斯分布:
如果 服从多变量高斯分布:
其中:
- 是均值向量
- 是协方差矩阵
参数估计:
|def fitMultivariateGaussian(X): """ 拟合多变量高斯分布 """ mu = np.mean(X, axis=0) Sigma = np.cov(X.T) return mu, Sigma def multivariateGaussianFull(X, mu, Sigma): """ 计算多变量高斯分布的概率密度 """ n = len(mu) X_centered = X - mu det_Sigma =
多变量高斯分布的优势:
能够捕捉特征之间的相关性。比如,CPU使用率和内存使用率通常正相关,多变量模型能建模这种相关性。
何时使用多变量模型:
- 特征之间有明显相关性
- 训练样本数量充足(,最好 )
- 有足够的计算资源(协方差矩阵的计算和求逆开销较大)
何时使用独立特征模型:
- 特征相对独立
- 训练样本较少
- 需要计算效率
- 通过手动构造组合特征已经捕捉了相关性
实践案例
案例:网络入侵检测
|# 特征:网络连接的各项指标 features = [ 'duration', # 连接持续时间 'src_bytes', # 源到目标的字节数 'dst_bytes', # 目标到源的字节数 'wrong_fragment', # 错误的分片数 'urgent', # 紧急包的数量 'hot', # 访问热点资源的次数 # ... 更多特征 ] # 训练集:正常网络流量 X_train = loadNormalTraffic() # 拟合异常检测模型 mu, sigma2 = fitGaussian(X_train) # 实时监控 while
特征工程技巧:
-
组合特征:创建有意义的比率和组合
- CPU使用率 / 网络流量
- 错误率 = 失败请求数 / 总请求数
-
非高斯特征的变换:
- 对数变换:
- 幂变换: 或
异常检测是无监督学习的重要应用,在安全、质量控制、系统监控等领域发挥着关键作用。通过建立正常行为的概率模型,我们能够自动识别不寻常的模式,及时发现问题。掌握异常检测,你就拥有了一个强大的工具来处理各种需要识别“异常”的场景。
在下一部分,我们将学习推荐系统——这个技术支撑着现代互联网的个性化服务,从电商的商品推荐到视频网站的内容推荐,再到社交媒体的信息流。推荐系统巧妙地结合了协同过滤、矩阵分解等技术,是机器学习的精彩应用。
小练习
-
问题诊断和解决方案:根据以下情况,诊断问题并提出解决方案。
你训练了一个模型,得到:
- 训练误差:5%
- 验证误差:25%
这是什么问题?应该如何解决?
答案:
诊断:高方差(过拟合)
判断依据:
- 训练误差很低(5%)- 模型在训练集上表现很好
- 验证误差很高(25%)- 模型在新数据上表现差
- 训练误差和验证误差差距大(20%)- 典型的过拟合特征
解决方案(按优先级):
-
获取更多训练数据 ✓ 最有效
- 更多数据能帮助模型学习真实模式而非噪声
-
减少特征数量 ✓
- 手动选择重要特征
- 使用PCA降维
-
增加正则化参数λ ✓
- 增大λ来惩罚复杂模型
-
使用更简单的模型 ✓
- 减少神经网络层数
- 减少多项式次数
不应该做的:
- ✗ 增加特征(会让过拟合更严重)
- ✗ 减小正则化参数(会让过拟合更严重)
- ✗ 训练更长时间(模型已经学得够好了)
Python诊断代码:
|def diagnose_model(train_error, val_error): gap = val_error - train_error if train_error > 0.15: # 高偏差 if gap < 0.05: return "欠拟合(高偏差)" else:
-
学习曲线分析:分析以下学习曲线,判断问题类型。
随着训练样本数量增加:
- 训练误差:从10%缓慢上升到18%
- 验证误差:从60%缓慢下降到20%
- 两条曲线在20%附近趋于平缓,但仍有差距
这是什么问题?解决方案是什么?
答案:
诊断:轻度高方差(过拟合),可能混合轻度高偏差
学习曲线特征分析:
-
训练误差上升(10% → 18%)
- 正常现象:更多数据使得完美拟合更难
- 说明模型没有明显欠拟合
-
验证误差下降(60% → 20%)
- 好现象:更多数据改善了泛化能力
- 但最终仍有差距(训练18% vs 验证20%)
-
曲线趋于平缓
- 说明:更多数据的边际收益递减
- 关键问题:曲线平缓但未收敛到理想值
判断:
- 如果目标误差是5%,那么18-20%说明模型偏差也较高
- 训练和验证误差的小差距(2%)表明方差不是主要问题
- 结论:可能需要更复杂的模型(增加特征/提高模型容量)
解决方案:
-
如果目标误差可接受(如15%):
- 当前模型已经不错
- 可以尝试获取更多数据进一步缩小gap
-
如果目标误差更低(如5%):
- 增加特征数量
- 使用更复杂的模型(更多隐藏层/神经元)
- 减小正则化参数λ
- 尝试多项式特征
典型学习曲线模式:
|高方差(过拟合): 训练误差:很低且平 验证误差:高且有大gap 解决:更多数据有帮助 高偏差(欠拟合): 训练误差:高且平 验证误差:高且gap小 解决:更多数据帮助不大,需要更复杂模型 理想状态: 两条曲线都低且接近 差距很小