推荐系统 - 个性化推荐算法 | 自在学推荐系统
打开电商网站,它知道你可能喜欢什么商品;打开视频平台,它推荐你可能想看的内容;打开音乐APP,它为你定制专属歌单。这些个性化推荐的背后,是推荐系统(Recommender Systems)在工作。
推荐系统是机器学习最成功的商业应用之一。它们不仅提升了用户体验,也为平台创造了巨大的商业价值。研究表明,Netflix有75%的观看来自推荐,Amazon有35%的销售来自推荐。好的推荐系统能够在海量内容中帮助用户发现他们真正喜欢的东西。
问题描述
推荐系统的基本设定:
假设有:
- nu 个用户
- nm 个物品(电影、商品、歌曲等)
- 评分矩阵 R:Rij 表示用户 i 对物品 j 的评分(如1-5星)
关键观察:评分矩阵是稀疏的——大多数用户只对少数物品评分,矩阵中大部分元素是未知的。
目标:预测用户对未评分物品的评分,推荐高分物品。
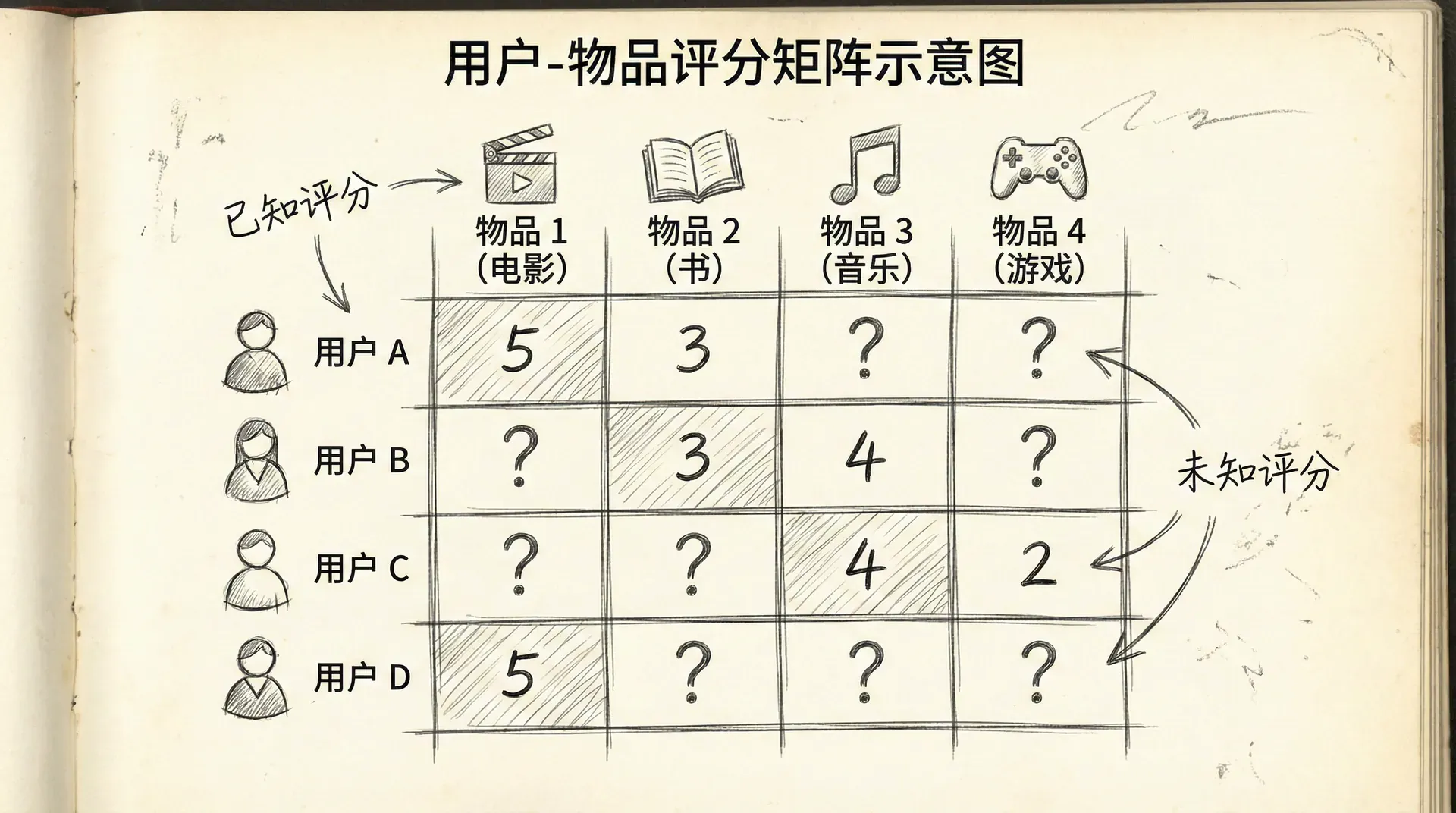
符号约定:
- r(i,j)=1 如果用户 i 对物品 j 评过分,否则为0
- y(i,j) 是用户 对物品 的评分
推荐系统解决的是一个非常特殊的预测问题:我们要为每个用户预测他对每个物品的评分,但每个用户只对极少数物品有已知评分。这种极端稀疏性是推荐系统的核心挑战。
基于内容的推荐
最直观的推荐方法是基于内容(Content-Based):如果知道物品的特征,就可以为每个用户学习一个偏好模型。
假设:我们知道每部电影的特征,比如:
- x1:浪漫程度(0-1)
- x2:动作程度(0-1)
对于用户 i,学习参数 θ(i),使得 (θ(i))Tx 能预测用户 对电影 的评分。
优化目标(对于用户 i):
θ(i)min
对所有用户:
minθ
这就是线性回归!对每个用户,用他评分过的电影训练一个线性回归模型。
问题:基于内容的方法需要手工定义物品特征。对于电影,我们可能能够定义"浪漫"、"动作"等特征,但对于很多领域(如新闻文章、社交网络帖子),定义有意义的特征很困难。
协同过滤提供了一个更优雅的解决方案:不需要手工特征,让数据自己告诉我们什么特征重要。
协同过滤算法
协同过滤的核心思想:如果用户A和用户B在过去的评分很相似,那么A喜欢的物品,B也可能喜欢。
换个角度:如果物品X和物品Y经常被同样的用户喜欢,那么喜欢X的用户也可能喜欢Y。
关键洞察:
假设我们知道用户的偏好向量 θ(i),可以学习物品特征 x(j):
minx(j)
反过来,如果我们知道物品特征 x(j),可以学习用户偏好 θ(i)(如前面所示)。
协同过滤的巧妙之处:同时优化物品特征和用户偏好!
协同过滤的优化目标:
同时对 x 和 θ 最小化这个目标。
算法步骤:
- 随机初始化 x(j) 和 θ(i) 为小的随机值
- 使用梯度下降(或其他优化算法)最小化 J
- 对于用户 i和物品 ,预测评分为
梯度计算:
∂xk(j)
∂θk(i)
import numpy as np
def cofiCostFunc(params, Y, R, num_users, num_movies, num_features, lambda_reg):
"""
协同过滤代价函数
params: 展开的参数向量 [X; Theta]
Y: 评分矩阵
R: 评分指示矩阵
"""
# 恢复参数
X = params[:num_movies * num_features].reshape(num_movies, num_features)
Theta = params[num_movies * num_features:].reshape(num_users, num_features)
# 计算代价
predictions = X @ Theta.T
errors = (predictions
低秩矩阵分解
协同过滤可以从矩阵分解的角度理解。
评分矩阵 Y 可以近似分解为两个矩阵的乘积:
Y≈XΘT
其中:
- X 是 nm×k 矩阵(每行是一个物品的特征向量)
- Θ 是 nu 矩阵(每行是一个用户的偏好向量)
这被称为低秩矩阵分解(Low-Rank Matrix Factorization),因为我们用两个低秩矩阵的乘积来近似原始矩阵。
向量化实现:
def predictRatings(X, Theta):
"""
预测所有评分
返回: num_movies x num_users 的预测矩阵
"""
return X @ Theta.T
def recommendMovies(user_id, X, Theta, movie_names, num_recommendations=10):
"""
为用户推荐电影
"""
# 预测该用户对所有电影的评分
predictions = X @ Theta[user_id]
# 排序并选择top-K
top_indices = np.argsort(predictions)[::-1][:num_recommendations]
寻找相似物品:
物品 j 的特征向量是 x(j)。找到与它最相似的物品,就是找到特征向量最接近的物品:
相似度=∣∣x(i)−x(j)∣∣
def findSimilarMovies(movie_id, X, movie_names, num_similar=5):
"""
找到相似的电影
"""
# 计算与所有电影的距离
distances = np.sum((X - X[movie_id])**2, axis=1)
# 排序(排除自己)
similar_indices = np.argsort(distances)[1:num_similar+1]
print(f"\n与 '
均值归一化
在实际应用中,评分数据常常存在偏差。有些用户给分普遍偏高,有些偏低。均值归一化可以处理这个问题。
方法:
- 对每个物品,计算所有用户评分的均值 μj
- 用归一化后的评分 Ynorm=Y−μ 训练模型
- 预测时,加回均值:预测 =
def normalizeMeanRatings(Y, R):
"""
均值归一化
Y: 评分矩阵
R: 评分指示矩阵
"""
m, n = Y.shape
Ymean = np.zeros(m)
Ynorm = Y.copy()
for i in range(m):
idx = R[i, :] == 1
if np.sum(idx) > 0:
Ymean[i] = np.mean(Y[i, idx])
Ynorm[i, idx]
好处:
对于全新用户(还没有任何评分),预测值是物品的平均评分——一个合理的默认值。
实践案例:电影推荐
# 完整的电影推荐系统
class MovieRecommender:
def __init__(self, num_features=10, lambda_reg=1.0):
self.num_features = num_features
self.lambda_reg = lambda_reg
self.X = None
self.Theta = None
self.Ymean = None
def fit(self, Y, R, num_iters=400
协同过滤的好处在于它不需要关于物品的任何信息——不需要知道电影的类型、演员、导演。它纯粹从用户的行为中学习。这使得它可以发现意想不到的关联,推荐用户可能喜欢但自己不会想到的物品。
接下来
推荐系统是机器学习最成功的应用领域之一,也是一个持续创新的领域。从简单的协同过滤,到深度学习推荐模型,再到结合知识图谱的推荐,技术在不断进步。但核心思想——利用群体智慧进行个性化——始终如一。
在下一节课中,我们将学习如何处理大规模数据。当数据量达到百万、千万甚至亿级时,传统的批量梯度下降变得不可行。我们需要新的算法和技术来高效地训练模型。大规模机器学习是将算法应用到真实世界海量数据的关键。
小练习
-
问题诊断和解决方案:根据以下情况,诊断问题并提出解决方案。
你训练了一个模型,得到:
这是什么问题?应该如何解决?
答案:
诊断:高方差(过拟合)
判断依据:
- 训练误差很低(5%)- 模型在训练集上表现很好
- 验证误差很高(25%)- 模型在新数据上表现差
- 训练误差和验证误差差距大(20%)- 典型的过拟合特征
解决方案(按优先级):
-
获取更多训练数据 ✓ 最有效
-
减少特征数量 ✓
-
增加正则化参数λ ✓
-
使用更简单的模型 ✓
不应该做的:
- ✗ 增加特征(会让过拟合更严重)
- ✗ 减小正则化参数(会让过拟合更严重)
- ✗ 训练更长时间(模型已经学得够好了)
Python诊断代码:
def diagnose_model(train_error, val_error):
gap = val_error - train_error
if train_error > 0.15: # 高偏差
if gap < 0.05:
return "欠拟合(高偏差)"
else:
-
学习曲线分析:分析以下学习曲线,判断问题类型。
随着训练样本数量增加:
- 训练误差:从10%缓慢上升到18%
- 验证误差:从60%缓慢下降到20%
- 两条曲线在20%附近趋于平缓,但仍有差距
这是什么问题?解决方案是什么?
答案:
诊断:轻度高方差(过拟合),可能混合轻度高偏差
学习曲线特征分析:
-
训练误差上升(10% → 18%)
- 正常现象:更多数据使得完美拟合更难
- 说明模型没有明显欠拟合
-
验证误差下降(60% → 20%)
- 好现象:更多数据改善了泛化能力
- 但最终仍有差距(训练18% vs 验证20%)
-
曲线趋于平缓
- 说明:更多数据的边际收益递减
- 关键问题:曲线平缓但未收敛到理想值
判断:
- 如果目标误差是5%,那么18-20%说明模型偏差也较高
- 训练和验证误差的小差距(2%)表明方差不是主要问题
- 结论:可能需要更复杂的模型(增加特征/提高模型容量)
解决方案:
-
如果目标误差可接受(如15%):
- 当前模型已经不错
- 可以尝试获取更多数据进一步缩小gap
-
如果目标误差更低(如5%):
- 增加特征数量
- 使用更复杂的模型(更多隐藏层/神经元)
- 减小正则化参数λ
- 尝试多项式特征
典型学习曲线模式:
高方差(过拟合):
训练误差:很低且平
验证误差:高且有大gap
解决:更多数据有帮助
高偏差(欠拟合):
训练误差:高且平
验证误差:高且gap小
解决:更多数据帮助不大,需要更复杂模型
理想状态:
两条曲线都低且接近
差距很小
i
θ(i) 是用户 i 的偏好向量 x(j) 是物品 j 的特征向量 (j)
21
j:r(i,j)=1∑
((
θ(i)
)T
x(j)
−
y(i,j))2+
2λk=1∑n(θk(i))2
(1)
,
...
,
θ(nu)
21
∑i=1nu
∑j:r(i,j)=1
((
θ(i)
)T
x(j)
−
y(i,j))2+
2λ∑i=1nu∑k=1n(θk(i))2
21
∑i:r(i,j)=1
((
θ(i)
)T
x(j)
−
y(i,j))2+
2λ∑k=1n(xk(j))2
J(x(1),...,x(nm),θ(1),...,θ(nu))=21(i,j):r(i,j)=1∑((θ(i))Ty(i,j))2+2λj=1∑nmk=1∑2λi=1∑nuk=1∑
j
(θ(i))Tx(j)
∂J
=
∑i:r(i,j)=1((θ(i))Tx(j)−
y(i,j))θk(i)+
λxk(j)
∂J
=
∑j:r(i,j)=1((θ(i))Tx(j)−
y(i,j))xk(j)+
λθk(i)
-
Y)
*
R
J = 0.5 * np.sum(errors ** 2) + \
0.5 * lambda_reg * (np.sum(Theta ** 2) + np.sum(X ** 2))
# 计算梯度
X_grad = (errors @ Theta) + lambda_reg * X
Theta_grad = (errors.T @ X) + lambda_reg * Theta
grad = np.concatenate([X_grad.ravel(), Theta_grad.ravel()])
return J, grad
def trainCollaborativeFiltering(Y, R, num_features, lambda_reg, num_iters=400):
"""
训练协同过滤模型
"""
num_movies, num_users = Y.shape
# 随机初始化
X = np.random.randn(num_movies, num_features)
Theta = np.random.randn(num_users, num_features)
initial_params = np.concatenate([X.ravel(), Theta.ravel()])
# 优化(这里简化使用梯度下降,实践中用更高级的优化器)
params = initial_params.copy()
alpha = 0.001
for i in range(num_iters):
J, grad = cofiCostFunc(params, Y, R, num_users, num_movies,
num_features, lambda_reg)
params -= alpha * grad
if (i+1) % 100 == 0:
print(f"迭代 {i+1}: 代价 = {J:.4f}")
# 恢复参数
X = params[:num_movies * num_features].reshape(num_movies, num_features)
Theta = params[num_movies * num_features:].reshape(num_users, num_features)
return X, Theta
×
k
k 是隐特征的数量(通常远小于 nm 和 nu)
print(f"\n为用户 {user_id} 推荐的电影:")
for i, idx in enumerate(top_indices, 1):
print(f"{i}. {movie_names[idx]} (预测评分: {predictions[idx]:.2f})")
return top_indices
{
movie_names[movie_id]
}
' 相似的电影:"
)
for i, idx in enumerate(similar_indices, 1):
print(f"{i}. {movie_names[idx]} (距离: {distances[idx]:.2f})")
return similar_indices
(θ(i))Tx(j)+μj
-=
Ymean[i]
return Ynorm, Ymean
):
"""
训练模型
Y: 评分矩阵 (num_movies x num_users)
R: 评分指示矩阵
"""
# 均值归一化
Ynorm, self.Ymean = normalizeMeanRatings(Y, R)
# 训练协同过滤
self.X, self.Theta = trainCollaborativeFiltering(
Ynorm, R, self.num_features, self.lambda_reg, num_iters
)
def predict(self, user_id, movie_id=None):
"""
预测评分
"""
if movie_id is None:
# 预测该用户对所有电影的评分
predictions = self.X @ self.Theta[user_id] + self.Ymean
return predictions
else:
# 预测特定评分
prediction = self.X[movie_id] @ self.Theta[user_id] + self.Ymean[movie_id]
return prediction
def recommend(self, user_id, num_recommendations=10):
"""
推荐电影
"""
predictions = self.predict(user_id)
top_indices = np.argsort(predictions)[::-1][:num_recommendations]
return top_indices, predictions[top_indices]
# 使用
recommender = MovieRecommender(num_features=10, lambda_reg=10)
recommender.fit(Y, R, num_iters=400)
# 为用户0推荐电影
recommendations, scores = recommender.recommend(user_id=0, num_recommendations=10)
return
"既欠拟合又过拟合"
else: # 低偏差
if gap > 0.10:
return "过拟合(高方差)"
else:
return "模型良好"
print(diagnose_model(0.05, 0.25)) # 输出:过拟合(高方差)
x(j)
−
n
(
xk(j)
)2
+
n
(
θk(i)
)2
