大规模机器学习

当数据量达到百万、千万甚至亿级规模时，传统的机器学习算法面临巨大挑战。批量梯度下降需要在每次迭代中遍历所有数据，计算量和内存需求都可能超出单机的承受能力。但恰恰是这些海量数据中蕴含着巨大的价值——更多的数据意味着更准确的模型。

大规模机器学习（Large Scale Machine Learning）研究如何在海量数据上高效地训练模型。

为什么需要大规模学习

“数据越多，模型越好”——这在很多情况下是成立的。研究表明，对于复杂任务，简单算法配上海量数据常常能超过复杂算法配上少量数据。

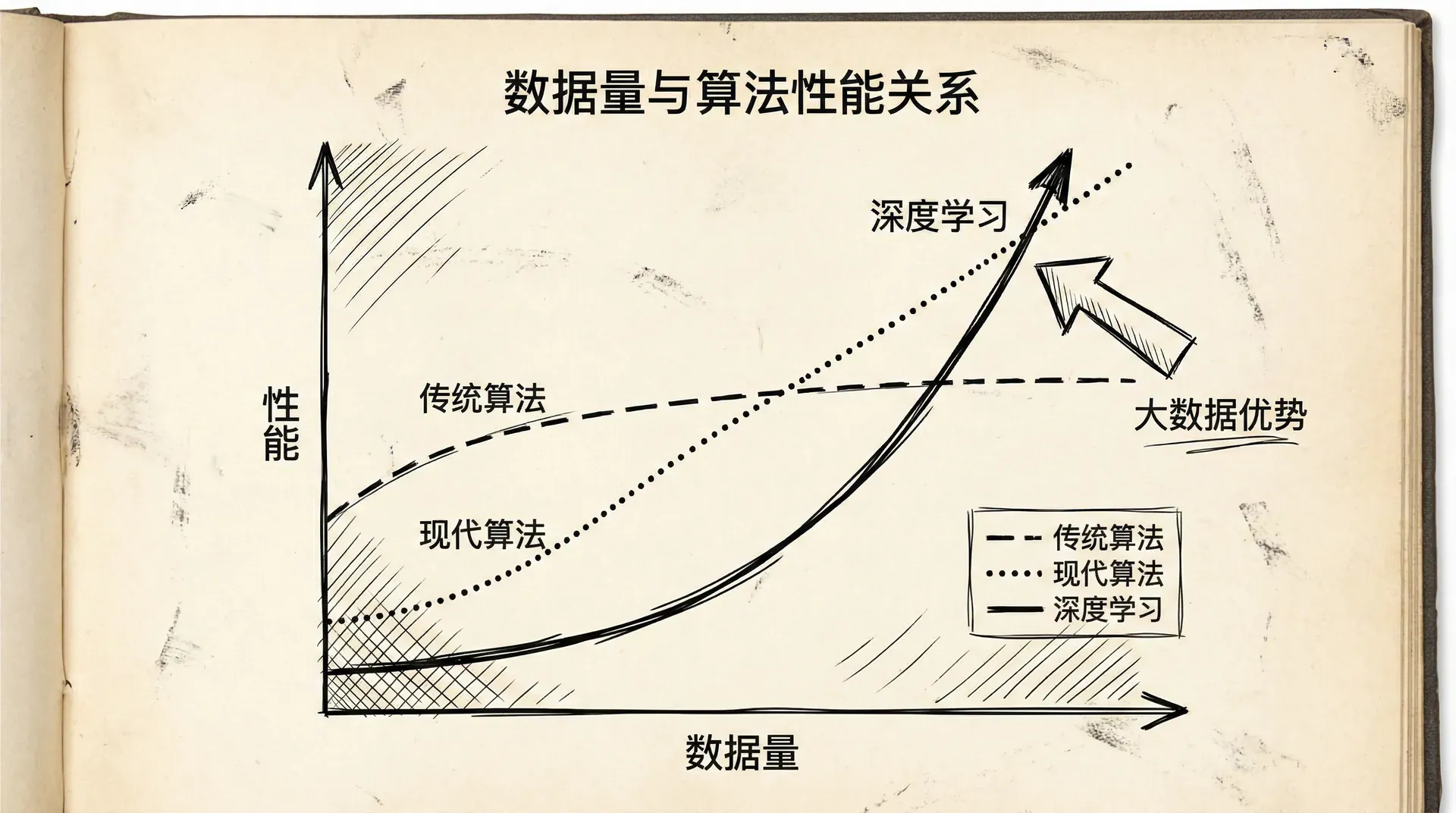
但大数据带来大挑战：

• 计算时间：批量梯度下降的一次迭代需要遍历所有样本，数百万样本可能需要数小时甚至数天
• 内存限制：所有数据可能无法一次性载入内存
• I/O瓶颈：从磁盘读取大量数据可能成为瓶颈

在开始大规模学习前，我们应该问：真的需要这么多数据吗？

诊断方法：画学习曲线

如果学习曲线显示训练误差和验证误差都还在下降，说明更多数据可能有帮助。如果曲线已经平稳（高偏差），更多数据不会带来显著提升，应该改进模型而不是增加数据。

import numpy as np
import matplotlib.pyplot as plt
 
def plotLearningCurve(X, y, X_val, y_val, model):
    """
    画学习曲线
    """
    m = X.shape[0]
    train_errors = []
    val_errors = []
    
    # 逐步增加训练样本数量
    m_samples = np.linspace(100, m, 10).astype(int)
    
    for m_i in m_samples:
        # 用前m_i个样本训练
        model.fit(X[:m_i], y[:m_i])
        
        # 计算误差
        train_errors.append(computeError(X[:m_i], y[:m_i], model))
        val_errors.append(computeError(X_val, y_val, model))
    
    plt.plot(m_samples, train_errors, label='训练误差')
    plt.plot(m_samples, val_errors, label='验证误差')
    plt.xlabel('训练样本数量')
    plt.ylabel('误差')
    plt.legend()
    plt.title('学习曲线')
    plt.show()

随机梯度下降

批量梯度下降（Batch Gradient Descent）在每次迭代中使用所有 $m$ 个样本：

$\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)}$

当 $m$ 很大（比如1亿）时，每次迭代都极其耗时。

随机梯度下降（Stochastic Gradient Descent, SGD） 每次只用一个样本更新：

def stochasticGradientDescent(X, y, theta, alpha, num_epochs):
    """
    随机梯度下降
    """
    m = len(y)
    cost_history = []
    
    for epoch in range(num_epochs):
        # 随机打乱数据
        indices = np.random.permutation(m)
        X_shuffled = X[indices]
        y_shuffled = y[indices]
        
        # 对每个样本更新一次
        for i in range(m):

SGD的特点：

优点：

• 速度快：不需要等到遍历完所有数据才更新
• 可以处理超大数据集：不需要一次性载入所有数据
• 可以在线学习：新数据到来时可以立即更新

缺点：

• 更新方向有噪声：基于单个样本的梯度不准确
• 收敛过程震荡：代价函数不会平滑递减，而是上下波动
• 可能无法精确收敛到最优值：会在最优值附近震荡

学习率调整：

为了让SGD更好地收敛，可以使用递减的学习率：

$\alpha = \frac{\text{const1}}{\text{iterationNumber} + \text{const2}}$

开始时学习率大，快速接近最优；后期学习率小，减少震荡。

def sgdWithDecayingLearningRate(X, y, theta, alpha0, num_epochs):
    """
    带学习率衰减的SGD
    """
    m = len(y)
    
    for epoch in range(num_epochs):
        indices = np.random.permutation(m)
        
        for i in range(m):
            # 学习率衰减
            alpha = alpha0 / (1 + epoch * m + i)

Mini-Batch梯度下降

Mini-Batch梯度下降是批量GD和随机GD的折衷：每次使用一小批（比如10-1000个）样本更新。

def miniBatchGradientDescent(X, y, theta, alpha, batch_size, num_epochs):
    """
    Mini-Batch梯度下降
    """
    m = len(y)
    
    for epoch in range(num_epochs):
        # 打乱数据
        indices = np.random.permutation(m)
        X_shuffled = X[indices]
        y_shuffled = y[indices]
        
        # 分批处理
        for i in range(0, m, batch_size):

Mini-Batch的优势：

• 向量化：可以利用向量化加速计算，比SGD快
• 稳定性：比SGD稳定，梯度估计更准确
• 并行化：batch中的样本可以并行处理，适合GPU
• 内存效率：比批量GD节省内存

Batch size的选择：

• 小batch（10-32）：更新频繁，收敛快，但不稳定
• 中等batch（64-256）：平衡速度和稳定性，最常用
• 大batch（512-1024+）：稳定，但需要更多内存，可能收敛慢

实践中，batch size常取2的幂次（32, 64, 128, 256），因为硬件对这些大小优化得更好。

检查收敛性

对于大数据集，我们不能每次迭代都计算整个训练集的代价（太慢了）。如何监控收敛？

方法：每处理N个样本，计算这N个样本的平均代价

比如，每1000个样本计算一次平均代价，画出趋势图。如果平均代价在下降，说明算法在收敛。

def sgdWithConvergenceMonitoring(X, y, theta, alpha, num_epochs, plot_interval=1000):
    """
    带收敛监控的SGD
    """
    m = len(y)
    costs = []
    iterations = []
    
    temp_cost = 0
    iteration = 0
    
    for epoch in range(num_epochs):
        indices = np.random.permutation(m)
        

收敛曲线的形状：

• 平滑下降：算法正常工作
• 震荡下降：可以尝试增大batch size或减小学习率
• 震荡不降：学习率太大，减小学习率
• 上升：学习率太大或代码有bug

在线学习

有些应用场景中，数据是持续不断到来的流。比如：

• 电商网站有源源不断的用户访问和交易
• 搜索引擎有持续的查询和点击
• 社交网络有不断的用户互动

在线学习（Online Learning）能够从这些数据流中持续学习，不断更新模型。

class OnlineLearner:
    def __init__(self, num_features, alpha=0.01):
        self.theta = np.zeros(num_features)
        self.alpha = alpha
        self.num_updates = 0
    
    def update(self, x, y):
        """
        用单个样本更新模型
        """
        # 预测
        h = self.predict(x)
        
        # 计算梯度并更新
        gradient 

在线学习的优势：

• 适应变化：用户偏好会变化，在线学习能跟上
• 无需存储所有数据：只需要当前样本
• 持续改进：模型不断进化，不需要定期重新训练
• 处理海量数据：数据太多无法存储时的唯一选择

应用场景：

• 广告点击率预测
• 推荐系统
• 垃圾邮件过滤
• 欺诈检测

Map-Reduce与数据并行

当单机无法处理数据时，我们需要分布式计算。Map-Reduce是一个强大的并行计算框架。

核心思想：

机器学习算法中的很多计算可以分解为：

1. Map：在不同机器上并行处理数据子集
2. Reduce：合并各机器的结果

批量梯度下降的Map-Reduce实现：

梯度计算可以分解：

$\frac{\partial J}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)}$

假设有4台机器，数据分成4份：

Map阶段（并行）：

• 机器1：计算前$m/4$个样本的梯度和 $temp^{(1)}_j$
• 机器2：计算接下来$m/4$个样本的梯度和 $temp^{(2)}_j$

Reduce阶段（合并）：

$\frac{\partial J}{\partial \theta_j} = \frac{1}{m} (temp^{(1)}_j + temp^{(2)}_j + temp^{(3)}_j + temp^{(4)}_j)$

然后更新参数：$\theta_j := \theta_j - \alpha \frac{\partial J}{\partial \theta_j}$

# 伪代码：Map-Reduce梯度下降
def map_function(data_chunk, theta):
    """
    在一台机器上执行，处理数据的一部分
    """
    gradient_sum = 0
    for (x, y) in data_chunk:
        gradient_sum += (predict(x, theta) - y) * x
    return gradient_sum
 
def reduce_function(gradient_sums, m, alpha, theta):
    """
    合并所有机器的结果
    """
    total_gradient = sum(gradient_sums) / m

适合Map-Reduce的算法：

很多机器学习算法可以并行化：

• 线性回归
• 逻辑回归
• 神经网络（前向和反向传播都可以并行）
• K-Means聚类

多核CPU：

即使在单机上，现代CPU有多个核心。可以用类似的思想利用多核并行：

• 把数据分成多份
• 每个核心处理一份
• 合并结果

现代深度学习框架（TensorFlow, PyTorch）自动利用多核和GPU并行。

大规模机器学习让我们能够充分利用海量数据的价值。通过随机梯度下降、Mini-Batch、在线学习和分布式计算，我们可以训练在几年前还不可想象的大模型。这些技术是现代AI系统的基础，从搜索引擎到推荐系统，从语音识别到图像理解。

在接下来的最后一节课中，我们将通过一个完整的应用案例，把所学的各种技术串起来，看看如何构建一个端到端的机器学习系统。

小练习

1. 问题诊断和解决方案：根据以下情况，诊断问题并提出解决方案。

   你训练了一个模型，得到：

   • 训练误差：5%
   • 验证误差：25%

   这是什么问题？应该如何解决？

def diagnose_model(train_error, val_error):
    gap = val_error - train_error
    
    if train_error > 0.15:  # 高偏差
        if gap < 0.05:
            return "欠拟合（高偏差）"
        else:

2. 学习曲线分析：分析以下学习曲线，判断问题类型。

   随着训练样本数量增加：

   • 训练误差：从10%缓慢上升到18%
   • 验证误差：从60%缓慢下降到20%
   • 两条曲线在20%附近趋于平缓，但仍有差距

   这是什么问题？解决方案是什么？

高方差（过拟合）：
  训练误差：很低且平
  验证误差：高且有大gap
  解决：更多数据有帮助
  
高偏差（欠拟合）：
  训练误差：高且平
  验证误差：高且gap小
  解决：更多数据帮助不大，需要更复杂模型
  
理想状态：
  两条曲线都低且接近
  差距很小