逻辑回归

到目前为止，我们学习的都是回归问题——预测连续的数值。但现实世界中，很多问题的答案是离散的类别：这封邮件是不是垃圾邮件？这个肿瘤是良性还是恶性？用户会不会点击这个广告？这些都是分类问题。

逻辑回归（Logistic Regression）是处理分类问题的经典算法。虽然名字中有“回归”二字，但它实际上是分类算法。逻辑回归不仅简单高效，而且是理解更复杂分类器（包括神经网络）的基础。事实上，深度神经网络的每个神经元本质上就是一个逻辑回归单元。

所以这节课我们将学习如何把线性回归的思想扩展到分类问题，如何设计适合分类的代价函数，以及如何将逻辑回归应用到多分类任务。

分类问题的特点

分类与回归的根本区别在于输出的性质。回归预测的是连续值，可以是任意实数；分类预测的是离散的类别标签。

最简单的是二分类（Binary Classification）问题，输出只有两个可能的类别。我们通常用0和1来表示这两个类别：

• $y = 0$：负类（Negative Class），比如"不是垃圾邮件"、"良性肿瘤"
• $y = 1$：正类（Positive Class），比如"是垃圾邮件"、"恶性肿瘤"

选择哪个类别作为正类是人为规定的，通常我们把想要检测的、比较罕见的那一类作为正类。

如果我们直接用线性回归来做分类会怎样？比如预测肿瘤是否恶性，用肿瘤大小作为特征。我们可能会得到一个线性模型 $h_\theta(x) = \theta_0 + \theta_1 x$。但这有几个问题：

线性回归的输出可以是任意实数，而我们需要的是0或1。我们可以设定一个阈值，比如0.5，大于0.5就预测为1，否则预测为0。但这很不自然，而且容易受异常值影响。

假设我们的训练数据中，肿瘤大小从1cm到10cm，用线性回归拟合得还不错。突然来了一个极端案例，肿瘤大小30cm，当然是恶性的（$y=1$）。加入这个点后，线性回归的直线会被"拉"向它，导致原来分类正确的点现在分类错了。

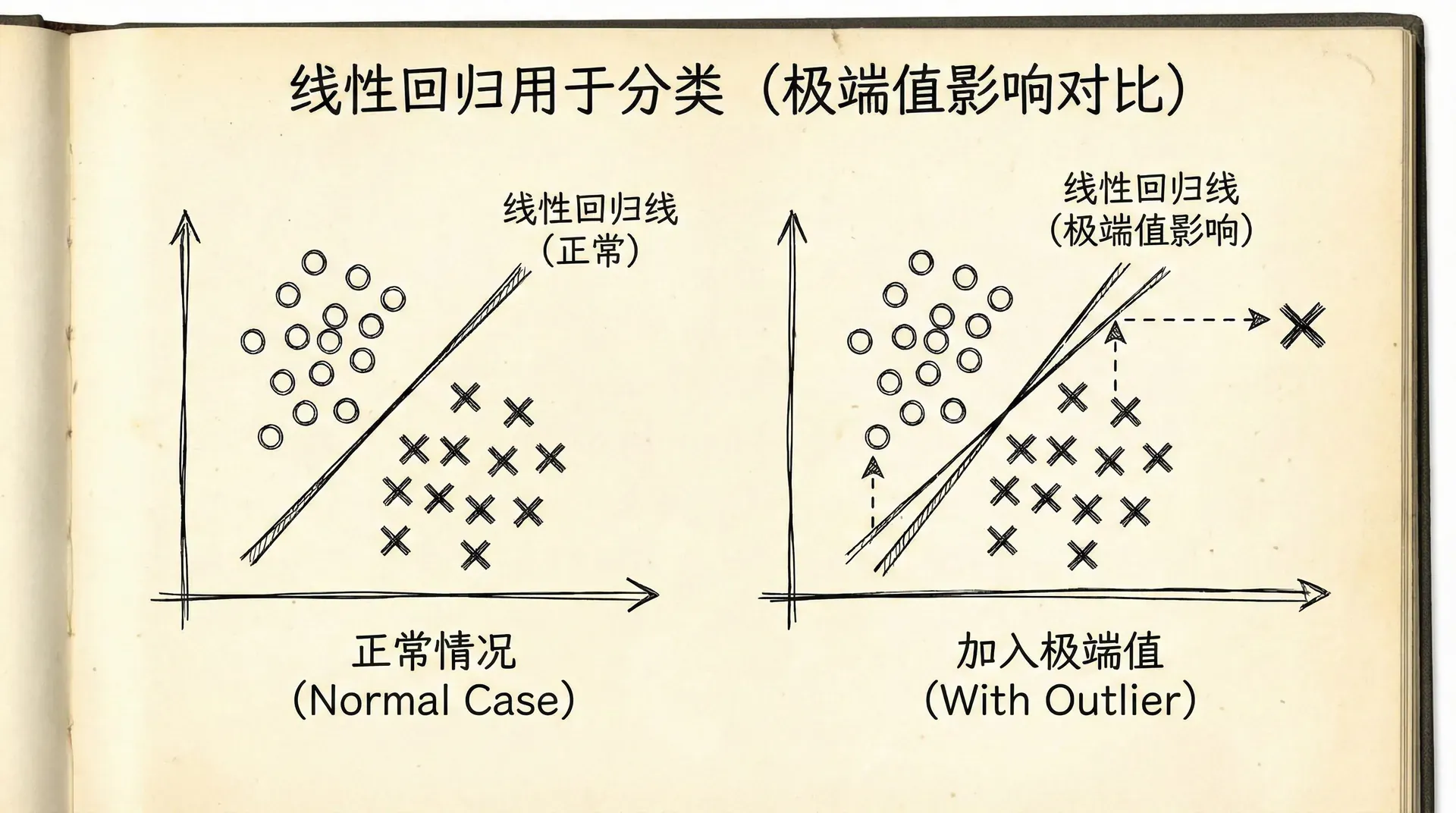
我们需要一个更适合分类的模型，它的输出应该自然地落在0和1之间，可以解释为“属于正类的概率”。这就是逻辑回归。

逻辑回归的假设函数

逻辑回归的关键是引入S型函数（Sigmoid Function），也称为逻辑函数（Logistic Function）：

$g(z) = \frac{1}{1 + e^{-z}}$

这个函数有很好的性质：

• 当 $z \to \infty$ 时，$g(z) \to 1$
• 当 $z \to -\infty$ 时，$g(z) \to 0$

逻辑回归的假设函数是：

$h_\theta(x) = g(\theta^T x) = \frac{1}{1 + e^{-\theta^T x}}$

我们先用线性组合 $\theta^T x$ 计算一个实数值，然后用sigmoid函数把它映射到(0, 1)区间。$h_\theta(x)$ 可以解释为：给定输入 $x$ 和参数 $\theta$，$y=1$ 的概率。

$h_\theta(x) = P(y=1 | x; \theta)$

相应地，$y=0$ 的概率是 $1 - h_\theta(x)$。

举个例子，假设我们预测肿瘤是否恶性，特征是肿瘤大小。如果对于某个肿瘤，$\theta^T x = 2$，那么：

$h_\theta(x) = \frac{1}{1 + e^{-2}} \approx 0.88$

模型认为这个肿瘤有88%的概率是恶性的。如果我们的决策阈值是0.5，我们会预测它是恶性。

决策边界（Decision Boundary）是使 $h_\theta(x) = 0.5$ 的点的集合。由于当 $\theta^T x = 0$ 时 $h_\theta(x) = 0.5$，决策边界就是 。

• 当 $\theta^T x \geq 0$ 时，$h_\theta(x) \geq 0.5$，预测 $y = 1$

对于二维特征 $x_1$ 和 $x_2$，如果 $\theta = [-3, 1, 1]^T$（包括截距项），决策边界是：

$-3 + x_1 + x_2 = 0$

即 $x_1 + x_2 = 3$，这是一条直线。在这条线的一边，预测为正类；另一边预测为负类。

逻辑回归的决策边界是线性的。但通过引入多项式特征（就像我们在线性回归中做的），可以得到非线性的决策边界。比如使用特征 $[1, x_1, x_2, x_1^2, x_2^2]$，参数 ，决策边界是：

$-1 + x_1^2 + x_2^2 = 0$

即 $x_1^2 + x_2^2 = 1$，这是一个圆！圆内预测为一类，圆外预测为另一类。

逻辑回归的代价函数

为什么不能用线性回归的均方误差作为逻辑回归的代价函数？因为逻辑回归的假设函数是非线性的（包含sigmoid），如果用均方误差，代价函数会是非凸的，有很多局部最小值，梯度下降可能无法找到全局最优解。

我们需要设计一个凸函数作为代价函数。对于单个样本，我们定义损失函数（Loss Function）：

理解这个定义：

• 当真实标签 $y=1$ 时，如果我们预测 $h_\theta(x) \to 1$（正确），损失接近0；如果预测 $h_\theta(x) \to 0$（错误），损失趋向无穷大，给予严厉惩罚。

这个损失函数巧妙地实现了：预测正确时损失小，预测错误时损失大，而且是凸函数，便于优化。

对于整个训练集，代价函数是所有样本损失的平均：

$J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} [y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)}))]$

这个公式巧妙地把两种情况合并了：当 $y^{(i)} = 1$ 时，第二项为0；当 $y^{(i)} = 0$ 时，第一项为0。

用向量化表示更简洁：

$J(\theta) = -\frac{1}{m} [y^T \log(h) + (1-y)^T \log(1-h)]$

其中 $h = g(X\theta)$ 是所有样本的预测概率向量。

梯度下降与优化

逻辑回归的代价函数看起来复杂，但求梯度后形式却很简洁。通过求导（这里省略推导过程），我们得到：

$\frac{\partial J}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)}$

用向量化表示：

$\nabla J = \frac{1}{m} X^T (g(X\theta) - y)$

这个形式和线性回归的梯度惊人地相似！唯一的区别是这里的 $h_\theta(x)$ 是sigmoid函数，而线性回归中是线性函数。

梯度下降的更新规则：

$\theta := \theta - \alpha \frac{1}{m} X^T (g(X\theta) - y)$

实现代码：

|
import numpy as np
 
def sigmoid(z):
    """Sigmoid函数"""
    return 1 / (1 + np.exp(-z))
 
def computeCost(X, y, theta):
    """计算逻辑回归的代价函数"""
    m = len(y)
    h = sigmoid(X @ theta)
    # 避免log(0)的情况，加一个很小的数
    epsilon = 1e-10
    cost = (-

逻辑回归也可以使用高级优化算法，它们通常比梯度下降更快：

• 共轭梯度法（Conjugate Gradient）：不需要手动选择学习率，收敛更快。
• BFGS和L-BFGS：拟牛顿法，利用二阶导数信息，收敛速度快，适合中大规模问题。

这些算法的原理比较复杂，但在实践中我们可以直接调用库函数。在Octave中：

|
% 定义代价函数和梯度函数
function [J, grad] = costFunction(theta, X, y)
  m = length(y);
  h = sigmoid(X * theta);
  J = (-1/m) * (y' * log(h) + (1-y)' * log(1-h));
  grad = (1/m) * X' * (h - y);
end
 
% 使用高级优化算法
options = optimset('GradObj', 'on', 'MaxIter', 400);
[theta, cost] = fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);

fminunc 是无约束优化函数，它会自动选择优化算法并调整参数，我们只需要提供代价函数和梯度的计算方法。

多元分类：一对多策略

到目前为止我们处理的都是二分类。如果有多个类别怎么办？比如手写数字识别，有0-9共10个类别；邮件分类，可能有工作、私人、促销、垃圾邮件等多个类别。

一种自然的扩展是一对多（One-vs-All或One-vs-Rest）策略。基本思想是：对于K个类别，训练K个二分类器，第i个分类器把类别i作为正类，其他所有类别作为负类。

具体步骤：

1. 对每个类别 $i = 1, 2, ..., K$，训练一个逻辑回归分类器 $h_\theta^{(i)}(x)$，预测 $y=i$ 的概率

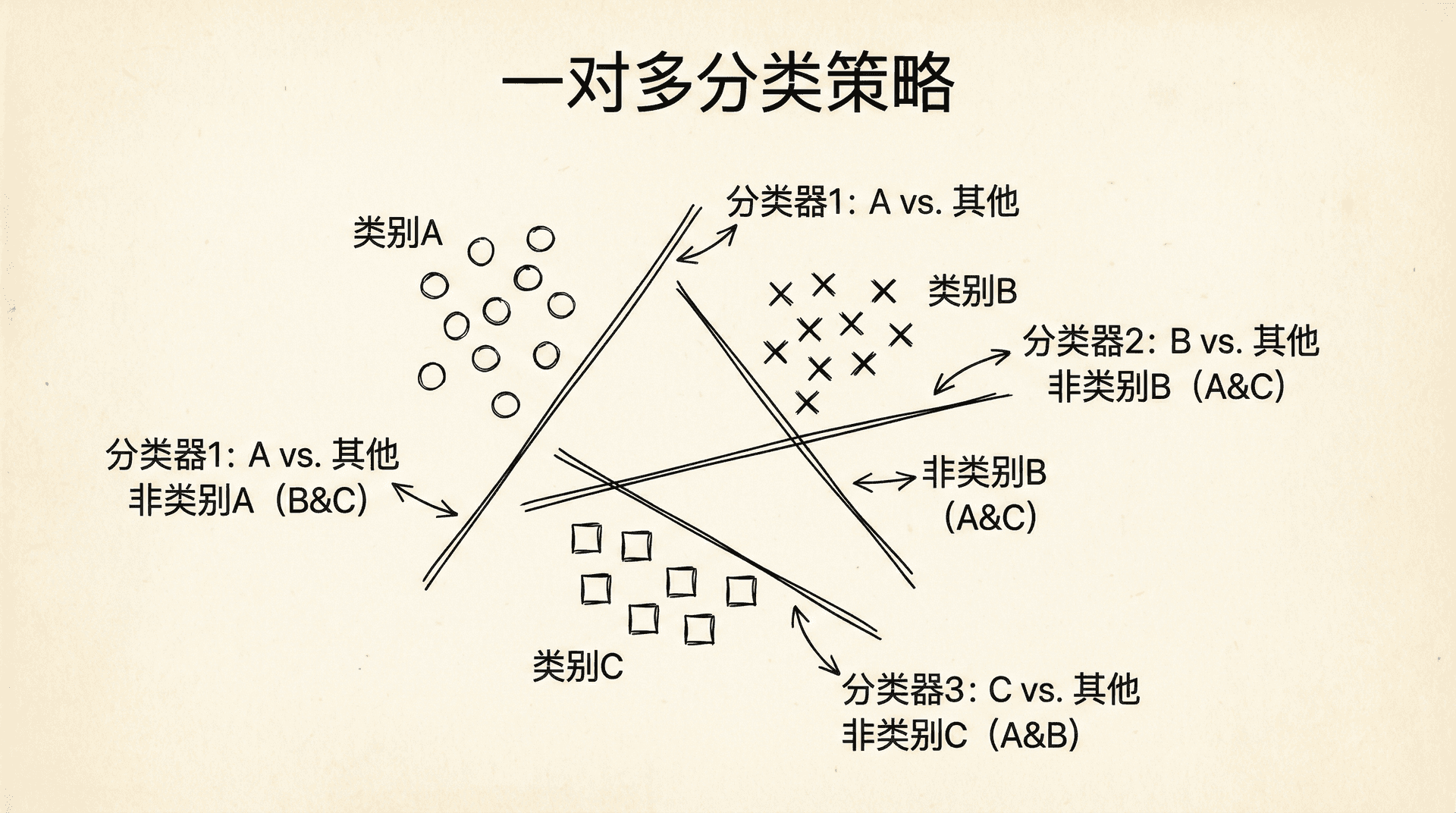
代码实现：

|
def oneVsAll(X, y, numLabels, lambda_reg):
    """
    训练多个一对多分类器
    X: 特征矩阵
    y: 标签（1, 2, ..., numLabels）
    numLabels: 类别数量
    lambda_reg: 正则化参数
    返回：所有分类器的参数矩阵
    """
    m, n = X.shape
    all_theta = np.zeros((numLabels, n))
    
    for i in range(numLabels):
        # 创建二分类标签：类别i为1，其他为0
        binary_y = (y == i).astype(int)
        
        # 训练第i个分类器
        initial_theta 

一对多策略简单有效，适用于类别不太多的情况。但当类别数量很大时，需要训练很多分类器，计算和存储开销会增大。这时可以考虑其他方法，比如softmax回归（多分类逻辑回归的直接扩展）或多类支持向量机。

接下来

在下一个部分，我们将学习正则化技术。我们会看到，过于复杂的模型容易过拟合，而正则化可以控制模型复杂度，提高泛化能力。正则化不仅适用于线性回归，也适用于逻辑回归和其他算法，是机器学习实践中的重要技术。

逻辑回归虽然简单，但它的思想深刻而广泛。sigmoid函数、最大似然估计、概率解释、一对多策略，这些概念会在后续的神经网络、深度学习中反复出现。深度神经网络可以看作是多层逻辑回归的堆叠和组合。掌握逻辑回归，你就为理解更复杂的模型打下了坚实基础。

小练习

1. 计算逻辑回归的代价函数：给定训练数据，手动计算逻辑回归的代价函数值。

   数据：

   $x$	$y$ (真实标签)
   2	1
   3	1
   1	0

   模型参数：$\theta_0 = -3$，$\theta_1 = 1$

2. 实现一对多分类：假设你要实现一个识别数字0-2的分类器（3个类别）。

   给定一个样本 $x = [2, 3]$，三个二分类器的输出分别为：

   • 分类器1（类别0 vs 其他）：$h_{\theta^{(1)}}(x) = 0.1$

逻辑回归假设函数：$h_\theta(x) = \frac{1}{1 + e^{-(\theta_0 + \theta_1 x)}}$

代价函数：$J(\theta) = -\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}\log(h_\theta(x^{(i)})) + (1-y^{(i)})\log(1-h_\theta(x^{(i)}))]$

样本2：$x=3, y=1$ $z = -3 + 1 \times 3 = 0$ $h_\theta(3) = \frac{1}{1+e^0} = \frac{1}{2} = 0.5$

样本3：$x=1, y=0$ $z = -3 + 1 \times 1 = -2$ $h_\theta(1) = \frac{1}{1+e^{-(-2)}} = \frac{1}{1+e^2} \approx \frac{1}{8.389} \approx 0.119$

步骤2：计算每个样本的代价

样本1（$y=1$）： $\text{cost}_1 = -[1 \times \log(0.269) + 0 \times \log(0.731)] = -\log(0.269) \approx 1.313$

样本2（$y=1$）： $\text{cost}_2 = -[1 \times \log(0.5) + 0 \times \log(0.5)] = -\log(0.5) \approx 0.693$

样本3（$y=0$）： $\text{cost}_3 = -[0 \times \log(0.119) + 1 \times \log(0.881)] = -\log(0.881) \approx 0.127$

步骤3：计算平均代价 $J(\theta) = \frac{1}{3}(1.313 + 0.693 + 0.127) = \frac{2.133}{3} \approx 0.711$

代价函数值约为 0.711

理解代价函数：

• 当 $y=1$ 时，如果 $h_\theta(x)$ 接近1，代价接近0（预测正确）
• 当 $y=1$ 时，如果 $h_\theta(x)$ 接近0，代价趋向无穷（预测错误）
• 当 $y=0$ 时，如果 $h_\theta(x)$ 接近0，代价接近0（预测正确）
• 当 $y=0$ 时，如果 $h_\theta(x)$ 接近1，代价趋向无穷（预测错误）

Python验证代码：

请问应该将这个样本分类为哪个类别？为什么？

本题分析：

比较三个分类器的输出：

• $h_{\theta^{(1)}}(x) = 0.1$ （类别0的概率）
• $h_{\theta^{(2)}}(x) = 0.7$ （类别1的概率）← 最大
• $h_{\theta^{(3)}}(x) = 0.2$ （类别2的概率）

因为分类器2的输出最高，所以应该将样本分类为类别1。

直观理解：

• 分类器2给出70%的置信度认为这是类别1
• 分类器3给出20%的置信度认为这是类别2
• 分类器1只给出10%的置信度认为这是类别0
• 我们选择最有"信心"的分类器

Python实现：

完整的一对多分类流程：

注意事项：

• 虽然逻辑回归输出"概率"，但在一对多设置中，这些"概率"并不保证和为1
• 它们只是相对的置信度分数
• 如果所有输出都很低（比如都小于0.3），可能表示样本不属于任何已知类别