正则化

在前面的学习中，我们已经掌握了线性回归和逻辑回归这两个基本算法。但在实际应用中，我们常常会遇到一个棘手的问题：模型在训练数据上表现很好，但在新数据上表现很差。这就是过拟合（Overfitting）问题，也是机器学习实践中最常见的挑战之一。

想象你在备考，如果只是死记硬背练习题的答案，考试遇到原题就能答对，但遇到新题就不会做。机器学习模型也是如此——如果模型过于复杂，它可能“记住”了训练数据的细节和噪声，而没有学到真正的规律。正则化（Regularization）就是解决这个问题的重要技术。

正则化的核心思想是：在优化目标中增加对模型复杂度的惩罚，迫使模型保持简单，从而提高泛化能力。所以这个部分我们将深入理解过拟合的本质，学习正则化的原理和实现，并将其应用到线性回归和逻辑回归中。

理解过拟合问题

让我们通过一个具体的例子来理解过拟合。假设我们要根据房屋面积预测房价，有6个训练样本。我们可以用不同复杂度的模型来拟合：

• 欠拟合（Underfitting）：用一条水平线 $h_\theta(x) = \theta_0$ 来拟合。这个模型太简单，无法捕捉面积与房价的关系，训练误差和测试误差都很大。这种情况也叫高偏差（High Bias）——模型对数据有强烈的先验假设（房价不随面积变化），导致系统性的预测偏差。
• 合适的拟合（Just Right）：用一条直线 $h_\theta(x) = \theta_0 + \theta_1 x$ 来拟合。模型复杂度适中，既能捕捉主要趋势，又不会被噪声误导。训练误差和测试误差都比较小且接近。
• 过拟合（Overfitting）：用一个高次多项式 $h_\theta(x) = \theta_0 + \theta_1 x + \theta_2 x^2 + ... + \theta_5 x^5$ 来拟合。这个模型完美地拟合了所有训练样本（训练误差接近0），但曲线扭曲得很厉害，对新数据的预测很差（测试误差很大）。这种情况也叫高方差（High Variance）——模型对训练数据的微小变化过于敏感。

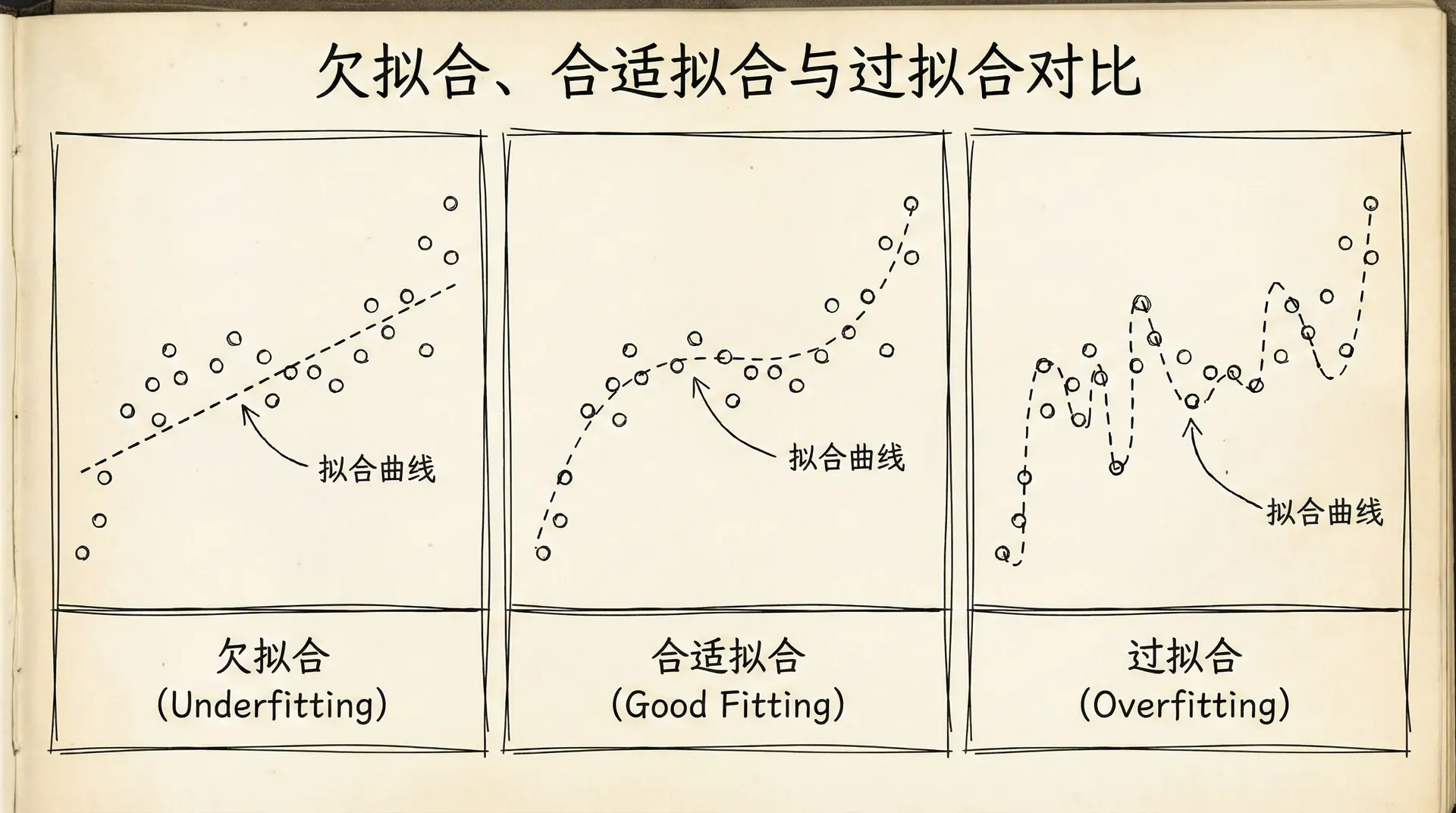
过拟合的根源是模型复杂度相对于数据量过高。导致过拟合的常见情况包括：

• 特征过多：如果我们有100个特征但只有50个样本，模型有很大的自由度，很容易"记住"每个样本。
• 多项式次数过高：高次多项式可以拟合几乎任何数据，但往往学到的是噪声而不是规律。
• 参数值过大：当参数值很大时，模型对输入的微小变化会产生很大的输出变化，导致不稳定。

如何发现过拟合？关键是在独立的测试集上评估模型。如果训练误差很小但测试误差很大，说明模型过拟合了。我们会在后续章节详细讨论如何评估模型和诊断问题。

解决过拟合有几种策略：

• 增加训练数据：更多的数据可以让模型学到更稳健的规律。但获取数据往往是昂贵或不可行的。
• 减少特征数量：手动选择重要的特征，或用算法自动选择。但这可能丢失有用的信息。
• 正则化：保留所有特征，但限制参数的大小。这是最常用且最有效的方法。

正则化的代价函数

正则化的基本思想是：在原来的代价函数上加一个惩罚项，惩罚过大的参数值。

对于线性回归，正则化后的代价函数是：

$J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2$

前半部分是原来的均方误差，衡量模型对训练数据的拟合程度。后半部分是正则化项（也叫惩罚项），是所有参数（除了截距 $\theta_0$）的平方和。$\lambda$ 是正则化参数，控制正则化的强度。

理解这个公式：优化算法要最小化这个代价函数，就需要在两个目标之间权衡：一是拟合训练数据（第一项小），二是保持参数值小（第二项小）。$\lambda$ 决定了这两个目标的相对重要性。

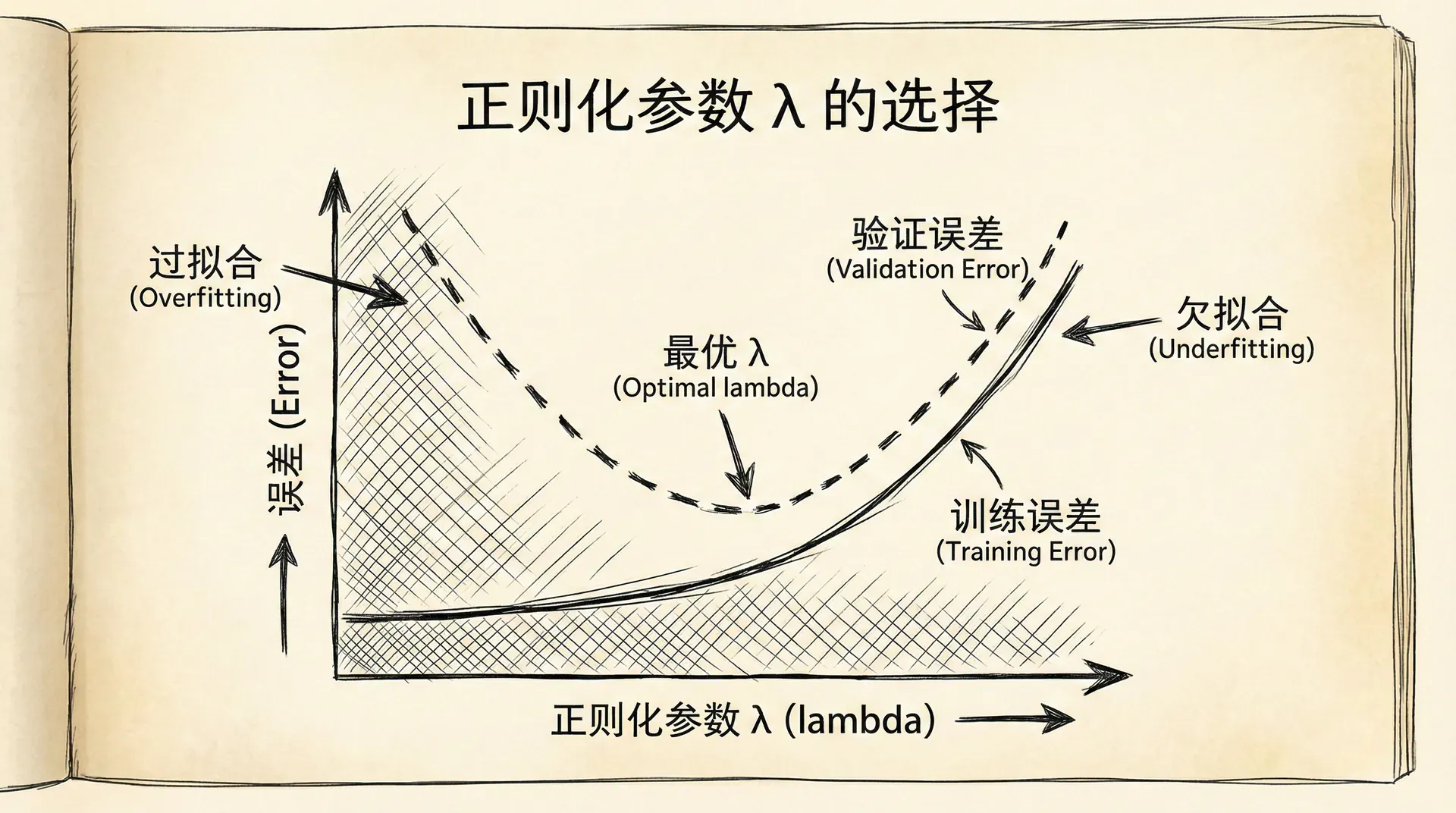
• $\lambda$ 很小：正则化项的影响很小，模型主要专注于拟合训练数据，可能导致过拟合。
• $\lambda$ 很大：正则化项占主导，模型被迫让所有参数接近0，可能导致欠拟合。
• $\lambda$ 适中：在拟合数据和保持简单之间取得平衡，得到泛化能力好的模型。

注意我们通常不惩罚截距项 $\theta_0$，因为它只是调整预测的整体水平，不影响模型的复杂度。

为什么惩罚参数的平方和能够减少过拟合？直观地说，较大的参数值会让模型对输入的变化很敏感，产生剧烈波动的预测函数（想象高次多项式的扭曲曲线）。通过限制参数大小，我们让模型变得"平滑"，对噪声不那么敏感。

从另一个角度看，正则化相当于给参数施加了先验约束："我们倾向于相信真实的参数值不会太大"。这种贝叶斯观点在统计学习理论中有深刻的根基。

正则化线性回归

将正则化应用到线性回归，我们需要修改梯度下降的更新规则。正则化代价函数对参数的梯度是：

$\frac{\partial J}{\partial \theta_0} = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x_0^{(i)}$

$\frac{\partial J}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} + \frac{\lambda}{m} \theta_j \quad (j \geq 1)$

注意 $\theta_0$ 的梯度没有正则化项，其他参数的梯度多了一项 $\frac{\lambda}{m} \theta_j$。

梯度下降的更新规则变为：

$\theta_0 := \theta_0 - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x_0^{(i)}$

$\theta_j := \theta_j - \alpha \left[ \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} + \frac{\lambda}{m} \theta_j \right] \quad (j \geq 1)$

将后者改写一下：

$\theta_j := \theta_j \left(1 - \alpha \frac{\lambda}{m}\right) - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)}$

这个形式很有启发性：每次更新，$\theta_j$ 首先乘以一个小于1的数（$1 - \alpha \frac{\lambda}{m}$），即先"收缩"一点，然后再按照梯度调整。这就是为什么正则化有时也叫权重衰减（Weight Decay）。

实现代码：

|
def computeCostRegularized(X, y, theta, lambda_reg):
    """计算正则化线性回归的代价函数"""
    m = len(y)
    h = X @ theta
    # 不惩罚theta[0]
    reg_term = (lambda_reg / (2*m)) * np.sum(theta[1:]**2)
    cost = (1/(2*m)) * np.sum((h -

正则化也适用于正规方程。正则化的正规方程解是：

$\theta = (X^TX + \lambda L)^{-1} X^T y$

其中 $L$ 是一个 $(n+1) \times (n+1)$ 的矩阵，除了左上角的元素是0，对角线上其他元素都是1，其余元素都是0：

这个公式还有一个额外的好处：即使 $X^TX$ 不可逆（比如特征数多于样本数），只要 $\lambda > 0$，$(X^TX + \lambda L)$ 就是可逆的。所以正则化不仅能防止过拟合，还能解决矩阵不可逆的问题。

正则化逻辑回归

正则化同样适用于逻辑回归。正则化的代价函数是：

$J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} [y^{(i)} \log(h_\theta(x^{(i)})) + (1-y^{(i)}) \log(1-h_\theta(x^{(i)}))] + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2$

前半部分是原来的逻辑回归代价函数，后半部分是正则化项。

梯度的计算与线性回归完全类似：

$\frac{\partial J}{\partial \theta_0} = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x_0^{(i)}$

$\frac{\partial J}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} + \frac{\lambda}{m} \theta_j \quad (j \geq 1)$

注意虽然梯度的形式和线性回归一样，但 $h_\theta(x)$ 的定义不同——这里是 $sigmoid(\theta^T x)$。

实现代码：

|
def sigmoid(z):
    return 1 / (1 + np.exp(-z))
 
def computeCostRegularizedLogistic(X, y, theta, lambda_reg):
    """计算正则化逻辑回归的代价函数"""
    m = len(y)
    h = sigmoid(X @ theta)
    epsilon = 1e-10
    
    # 逻辑回归的代价
    cost = (-1/m) * (y.T 

正则化逻辑回归在实践中非常常用。很多机器学习库（如scikit-learn）默认都会使用正则化。在使用这些库时，你会看到一个参数C，它是 $\frac{1}{\lambda}$ 的关系——$C$ 越小，正则化越强。

正则化的可视化

L1正则化与L2正则化

到目前为止我们讨论的正则化使用参数的平方和作为惩罚，这称为L2正则化（也叫岭回归，Ridge Regression）。还有另一种常用的正则化方式，称为L1正则化（也叫Lasso）。

L1正则化使用参数绝对值的和作为惩罚：

$J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2 + \frac{\lambda}{m} \sum_{j=1}^{n} |\theta_j|$

L1和L2正则化有不同的特点：

L2正则化（Ridge）：

• 参数趋向于小的值，但通常不会变成精确的0
• 所有特征都会被保留，只是权重变小
• 对异常值相对稳定
• 数学上更容易处理（可导）

L1正则化（Lasso）：

• 倾向于让一些参数变成精确的0
• 自动进行特征选择，删除不重要的特征
• 当特征很多且只有少数重要时效果好
• 数学上稍复杂（在0处不可导）

L1正则化的特征选择性质很有用。如果我们有上千个特征但只有少数真正有用，L1正则化可以自动找出这些重要特征，把其他特征的系数设为0。这在高维数据分析中很有价值。

还有一种结合两者的方法，称为弹性网络（Elastic Net）：

$J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2 + \lambda_1 \sum_{j=1}^{n} |\theta_j| + \lambda_2 \sum_{j=1}^{n} \theta_j^2$

弹性网络同时具有L1的特征选择性和L2的稳定性。

在实践中如何选择：

• 如果特征数不多，或者所有特征都可能有用，用L2正则化
• 如果特征很多，且预期只有少数重要，用L1正则化
• 不确定时，可以尝试弹性网络，或者用交叉验证比较

正则化的直观理解

为什么正则化能防止过拟合？让我们从几个角度理解：

• 几何角度：在参数空间中，原来的优化是找代价函数最小的点。加入正则化后，我们要在满足“参数不能太大”的约束下找最小点。L2正则化的约束是一个球形区域（$\sum \theta_j^2 \leq C$），L1正则化的约束是一个菱形区域（$\sum |\theta_j| \leq C$）。最优解往往在约束边界上，这就是为什么L1正则化容易产生稀疏解（某些参数正好在坐标轴上，即为0）。

正则化是机器学习实践中最重要的技术之一。几乎所有现代机器学习算法都有某种形式的正则化。在深度学习中，除了L1/L2正则化，还有Dropout、Batch Normalization等其他正则化技术。但核心思想是一致的：控制模型复杂度，提高泛化能力。

在下一节课程中，我们将学习神经网络的基本结构。神经网络是更强大的模型，可以学习复杂的非线性关系。但同时，神经网络也更容易过拟合，正则化在神经网络训练中扮演着关键角色。我们会看到，逻辑回归实际上是最简单的神经网络。

小练习

1. 理解正则化参数的作用：考虑一个多项式回归模型，数据有10个样本。你尝试了不同的正则化参数 $\lambda$，得到以下结果：

   $\lambda$	训练误差	验证误差
   0	5	100
   1	10	20
   10	25	15
   100	80	70

   分析每个 $\lambda$ 值对应的模型状态（欠拟合/过拟合/合适），并选择最佳的 $\lambda$ 值。

2. 实现L2正则化的梯度：给定正则化的代价函数，推导并实现正则化线性回归的梯度。

   正则化代价函数： $J(\theta) = \frac{1}{2m}\left[\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})^2 + \lambda\sum_{j=1}^{n}\theta_j^2\right]$

$\lambda = 100$（过度正则化）：

• 训练误差：80（很高）
• 验证误差：70（又开始上升）
• 诊断：欠拟合
• 原因：正则化惩罚太强，模型变得过于简单，无法捕捉数据的真实模式
• 特征：训练误差和验证误差都很高

最佳选择：$\lambda = 10$

原因：

1. 验证误差最低（15）
2. 训练误差和验证误差的差距不大，说明模型泛化良好
3. 在偏差和方差之间取得了最佳平衡

正则化参数选择的一般规律：

|
λ 太小 → 过拟合 → 训练误差很低，验证误差很高
                   
λ 适中 → 最优 → 验证误差最低
                   
λ 太大 → 欠拟合 → 训练误差和验证误差都很高

Python实现参数选择：

实践建议：

• 使用网格搜索或随机搜索来寻找最佳 $\lambda$
• 常见的搜索范围：[0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10...]
• 在对数尺度上搜索效率更高
• 使用交叉验证来更可靠地评估每个 $\lambda$ 的性能

注意：$\theta_0$ 不参与正则化。

推导梯度表达式，并用Python实现。

对 $\theta_j$ ($j \geq 1$) 求偏导（需要正则化）： $\frac{\partial J}{\partial \theta_j} = \frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} + \frac{\lambda}{m}\theta_j$

向量化形式：

设 $X$ 是 $m \times (n+1)$ 的设计矩阵，$\theta$ 是 $(n+1) \times 1$ 的参数向量。

完整的梯度向量： $\nabla J = \frac{1}{m}X^T(X\theta - y) + \frac{\lambda}{m}\begin{bmatrix} 0 \\ \theta_1 \\ \theta_2 \\ \vdots \\ \theta_n \end{bmatrix}$

或者写成： $\nabla J = \frac{1}{m}X^T(X\theta - y) + \frac{\lambda}{m}\begin{bmatrix} 0 \\ \theta_{1:n} \end{bmatrix}$

Python实现：

关键点：

1. 正则化项只对 $\theta_1, \theta_2, ..., \theta_n$ 起作用
2. $\theta_0$（偏置项）不参与正则化
3. 正则化会"收缩"参数值，防止参数过大
4. $\lambda$ 越大，收缩效果越强

正则化的效果：

• 参数值被"推向"零，但不会完全变为零（L2正则化）
• 模型变得更简单、更平滑
• 提高泛化能力，减少过拟合