5 / 18

Octave/Matlab教程

在前面的课程里，我们学习了线性回归的理论和数学原理。理论固然重要，但机器学习最终要落实到实践——我们需要编写代码来实现算法，处理真实数据，验证我们的想法。这就需要合适的编程工具。

Octave（和它的商业版本Matlab）是专门为数值计算设计的编程环境，特别擅长处理矩阵和向量运算。由于机器学习的核心就是矩阵运算，Octave成为了快速原型开发和算法验证的理想工具。即使你最终会用Python或其他语言实现生产系统，Octave也是学习和实验的好帮手——它的语法简洁直观，能让你把注意力集中在算法本身而不是编程细节上。

所以这节课我们将学习Octave的基本使用方法。我们会从最基础的操作开始，逐步深入到数据处理、计算和可视化。我们还会特别强调向量化编程——这不仅是Octave/Matlab的精髓，也是高效实现机器学习算法的关键。

Octave是开源免费的，Matlab是商业软件功能更强大但需要付费。对于学习机器学习来说，Octave完全够用，而且语法基本兼容。本部分的代码在两者中都能运行。当然，如果你更熟悉Python，也可以用NumPy——它的语法与Octave/Matlab很相似！

基本操作：入门第一步

启动Octave后，你会看到一个命令行界面，提示符通常是 >>。你可以像使用计算器一样输入表达式，Octave会立即计算并显示结果。

最基本的算术运算：


>> 5 + 3
ans = 8
 
>> 10 - 4
ans = 6
 
>> 7 * 6
ans = 42
 
>> 100 / 4
ans = 25
 
>> 2 ^ 8  % 幂运算
ans = 256

注意 % 后面的内容是注释，Octave会忽略它们。ans 是一个特殊变量，保存最近一次计算的结果。

逻辑运算返回1（真）或0（假）：


>> 5 > 3
ans = 1  % 真
 
>> 2 == 3
ans = 0  % 假
 
>> 7 ~= 5  % 不等于
ans = 1
 
>> (5 > 3) && (2 < 4)  % 逻辑与
ans = 1
 
>> (5 > 3) || (2 > 4)  % 逻辑或
ans = 1

变量赋值使用等号。变量名区分大小写，可以包含字母、数字和下划线，但必须以字母开头。


>> a = 5
a = 5
 
>> b = 10
b = 10
 
>> c = a + b
c = 15
 
>> x = 3; y = 4; z = 5;  % 分号抑制输出，可以在一行中写多个语句
 
>> z
z = 5

如果你不想看到每次计算的输出，在语句末尾加分号。这在处理大矩阵时很有用，否则屏幕会被大量数字淹没。

一些有用的内置函数：


>> pi  % 圆周率
ans = 3.1416
 
>> sin(pi/2)  % 正弦函数
ans = 1
 
>> log(1)  % 自然对数
ans = 0
 
>> exp(0)  % e的指数
ans = 1
 
>> abs(-5)  % 绝对值
ans = 5
 
>> sqrt(16)  % 平方根
ans = 4

查看工作空间中的变量，可以用 who 或 whos 命令：


>> who
Variables in the current scope:
a  b  c  x  y  z
 
>> whos
Variables in the current scope:
   Attr Name        Size                     Bytes  Class
   ==== ====        ====                     =====  ===== 
        a           1x1                          8  double
        b           1x1                          8  double
        c           1x1                          8  double

清除变量用 clear，清屏用 clc：


>> clear a  % 清除变量a
>> clear    % 清除所有变量
>> clc      % 清空屏幕

处理矩阵和向量

Octave最强大的地方就是矩阵操作。创建矩阵非常简单：


>> A = [1 2; 3 4; 5 6]  % 分号分隔行，空格或逗号分隔列
A =
   1   2
   3   4
   5   6
 
>> v = [1; 2; 3]  % 列向量
v =
   1
   2
   3
 
>> w = [1 2 3]  % 行向量
w =
   1   2   3

创建特殊矩阵：


>> zeros(2, 3)  % 2x3的零矩阵
ans =
   0   0   0
   0   0   0
 
>> ones(3, 2)  % 3x2的全1矩阵
ans =
   1   1
   1   1
   1   1
 
>> eye(4)  % 4x4的单位矩阵
ans =
   1   0   0   0
   0   1   0   0
   0   0   1   0
   0   0   0   1
 
>> rand(2, 2)  % 2x2的随机矩阵，元素在[0,1]之间
ans =
   0.81472   0.12699
   0.90579   0.91338
 
>> randn(2, 2)  % 2x2的随机矩阵，元素服从标准正态分布
ans =
   0.53767   0.86217
  -1.30768   0.31877

创建序列：


>> 1:5  % 从1到5，步长为1
ans =
   1   2   3   4   5
 
>> 0:0.5:2  % 从0到2，步长为0.5
ans =
   0.0000   0.5000   1.0000   1.5000   2.0000
 
>> linspace(0, 10, 5)  % 从0到10的5个等间隔数
ans =
   0.0000   2.5000   5.0000   7.5000   10.0000

查看矩阵的尺寸：


>> A = [1 2 3; 4 5 6]
A =
   1   2   3
   4   5   6
 
>> size(A)  % 返回行数和列数
ans =
   2   3
 
>> size(A, 1)  % 只返回行数
ans = 2
 
>> size(A, 2)  % 只返回列数
ans = 3
 
>> length(v)  % 向量的长度
ans = 3

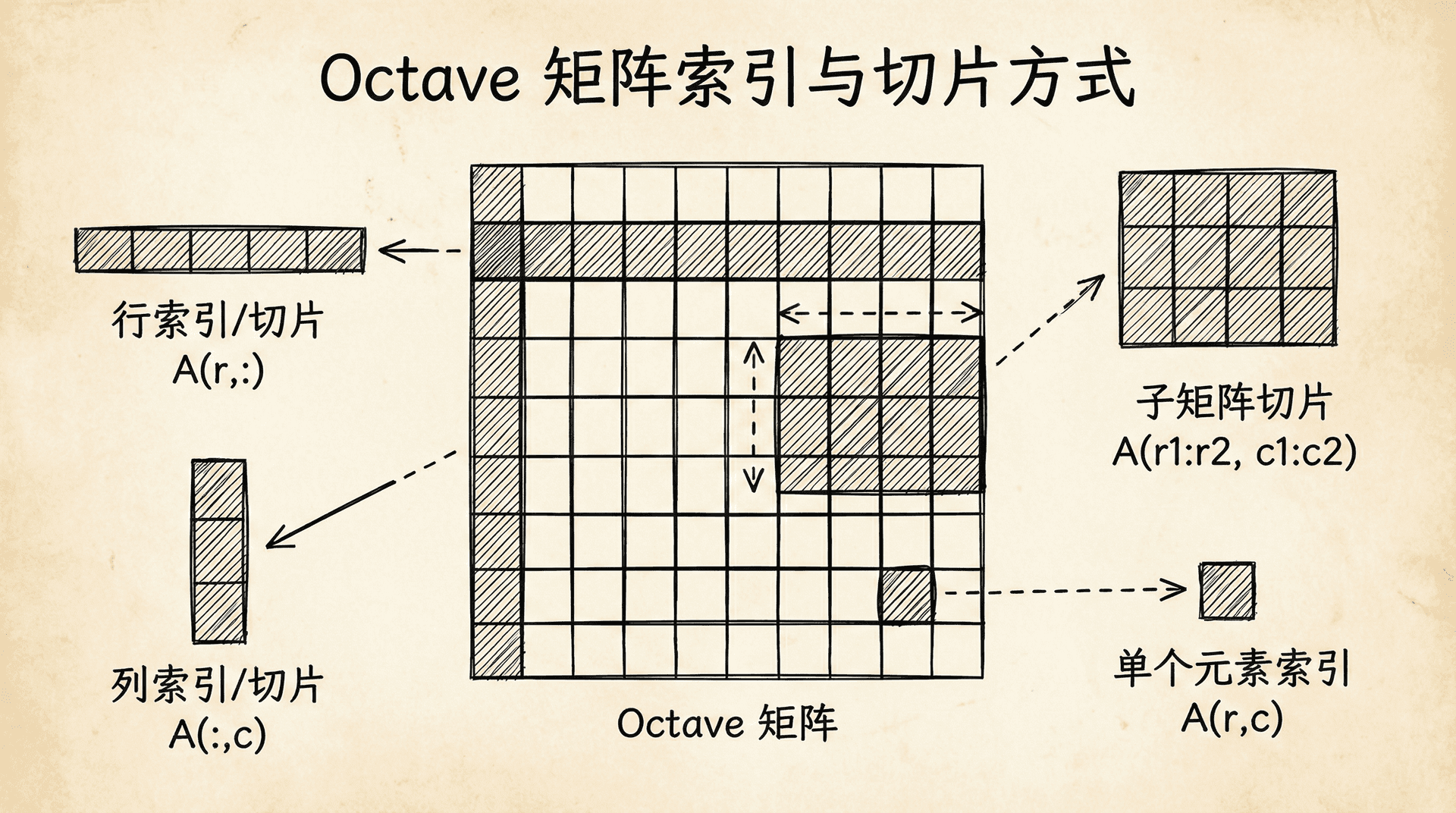
访问矩阵元素。注意Octave的索引从1开始（不像Python从0开始）：


>> A = [1 2 3; 4 5 6; 7 8 9]
A =
   1   2   3
   4   5   6
   7   8   9
 
>> A(2, 3)  % 第2行第3列的元素
ans = 6
 
>> A(3, :)  % 第3行的所有元素，冒号表示"所有"
ans =
   7   8   9
 
>> A(:, 2)  % 第2列的所有元素
ans =
   2
   5
   8
 
>> A([1 3], :)  % 第1行和第3行
ans =
   1   2   3
   7   8   9
 
>> A(:, 2:end)  % 第2列到最后一列，end表示最后一个索引
ans =
   2   3
   5   6
   8   9

修改矩阵元素：


>> A(2, 1) = 10  % 修改单个元素
A =
    1    2    3
   10    5    6
    7    8    9
 
>> A(:, 3) = [100; 200; 300]  % 修改整列
A =
     1     2   100
    10     5   200
     7     8   300

矩阵拼接：


>> A = [1 2; 3 4]
>> B = [5 6; 7 8]
 
>> [A B]  % 横向拼接
ans =
   1   2   5   6
   3   4   7   8
 
>> [A; B]  % 纵向拼接
ans =
   1   2
   3   4
   5   6
   7   8
 
>> A(:)  % 把矩阵展开成列向量
ans =
   1
   3
   2
   4

Octave中矩阵索引和切片的各种方式，包括行、列、子矩阵的选取

矩阵运算与计算

矩阵的加减乘除：


>> A = [1 2; 3 4]
>> B = [5 6; 7 8]
 
>> A + B  % 矩阵加法
ans =
    6    8
   10   12
 
>> A - B  % 矩阵减法
ans =
   -4   -4
   -4   -4
 
>> A * B  % 矩阵乘法（线性代数意义上的）
ans =
   19   22
   43   50
 
>> A .* B  % 元素对应相乘（点乘）
ans =
    5   12
   21   32

注意 * 和 .* 的区别！* 是矩阵乘法，要求维度匹配；.* 是元素级的乘法，对应元素相乘，要求矩阵尺寸相同。

类似地，有元素级的除法和幂运算：


>> A ./ B  % 元素对应相除
ans =
   0.20000   0.33333
   0.42857   0.50000
 
>> A .^ 2  % 每个元素平方
ans =
    1    4
    9   16

转置和逆矩阵：


>> A'  % 转置
ans =
   1   3
   2   4
 
>> inv(A)  % 逆矩阵
ans =
  -2.0000   1.0000
   1.5000  -0.5000
 
>> A * inv(A)  % 验证：A乘以A的逆等于单位矩阵
ans =
   1.0000e+00   0.0000e+00
  -8.8818e-16   1.0000e+00  % 注意数值误差

伪逆矩阵（对于不可逆矩阵也有定义）：


>> C = [1 2 3; 4 5 6]  % 非方阵
>> pinv(C)  % 伪逆
ans =
  -0.94444   0.44444
  -0.11111   0.11111
   0.72222  -0.22222

其他有用的矩阵函数：


>> A = [1 2 3; 4 5 6; 7 8 9]
 
>> sum(A)  % 每列求和
ans =
   12   15   18
 
>> sum(A, 2)  % 每行求和，2表示沿第2维（列方向）求和
ans =
    6
   15
   24
 
>> sum(sum(A))  % 所有元素求和
ans = 45
 
>> prod(A)  % 每列元素连乘
ans =
   28   80   162
 
>> max(A)  % 每列的最大值
ans =
   7   8   9
 
>> max(A, [], 2)  % 每行的最大值
ans =
   3
   6
   9
 
>> [val, idx] = max(A(:))  % 整个矩阵的最大值及其索引
val = 9
idx = 9  % 线性索引

逻辑运算可以应用到矩阵：


>> A = [1 2 3; 4 5 6]
>> A > 3  % 返回逻辑矩阵
ans =
   0   0   0
   1   1   1
 
>> find(A > 3)  % 找出满足条件的元素的索引
ans =
   2
   4
   6
 
>> A(A > 3)  % 选出满足条件的元素
ans =
   4
   5
   6

这种逻辑索引在数据处理中非常有用，比如找出所有房价超过300万的样本。

数据可视化

可视化是理解数据和算法的重要工具。Octave提供了强大的绘图功能。

最基本的绘图：


>> x = 0:0.01:2*pi;  % 创建x坐标
>> y = sin(x);  % 计算y坐标
>> plot(x, y);  % 绘制曲线
>> xlabel('x');  % x轴标签
>> ylabel('sin(x)');  % y轴标签
>> title('正弦函数');  % 图标题

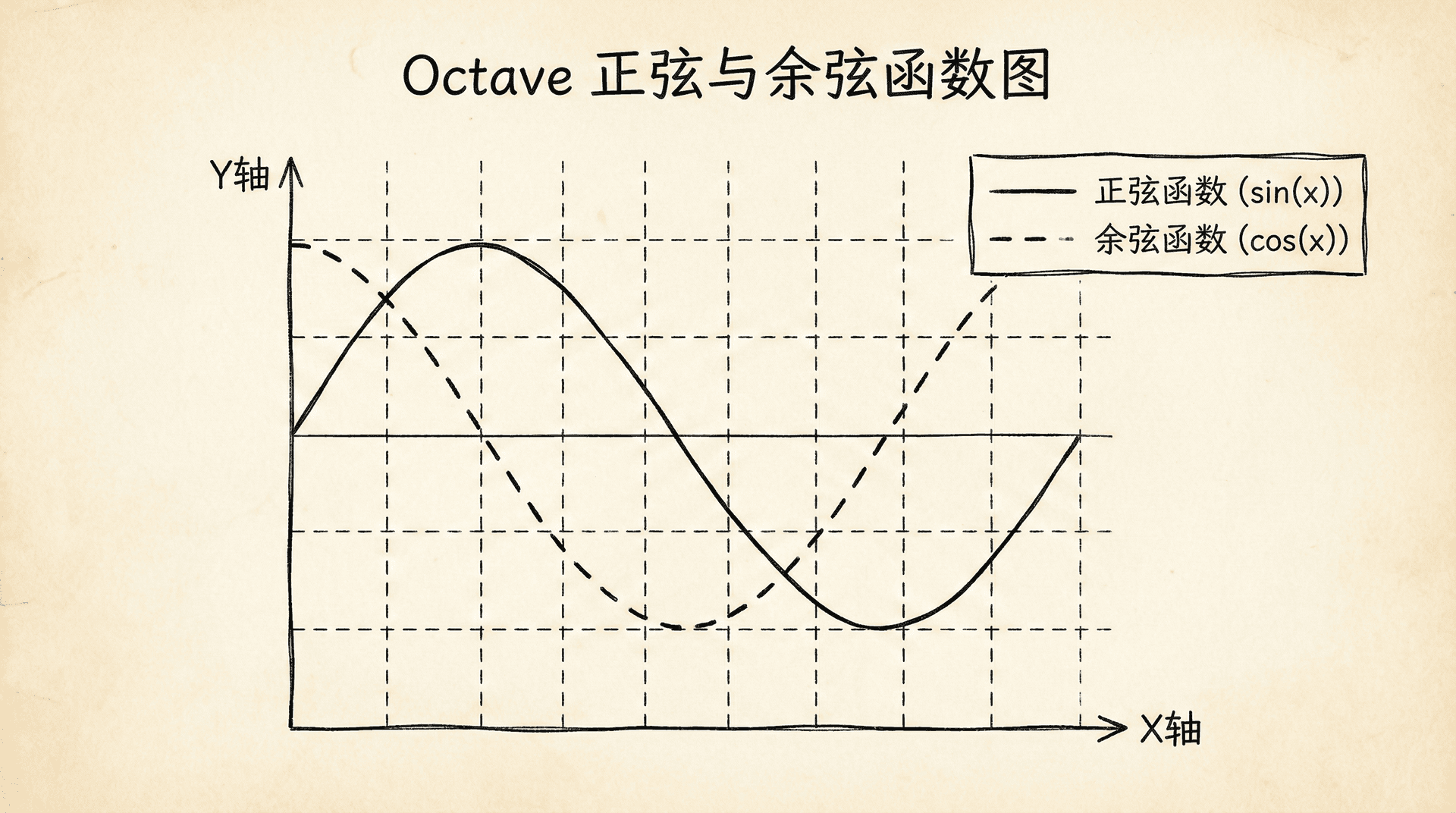
在同一个图中绘制多条曲线：


>> x = 0:0.01:2*pi;
>> y1 = sin(x);
>> y2 = cos(x);
>> plot(x, y1, 'r', x, y2, 'b--');  % 红色实线和蓝色虚线
>> legend('sin(x)', 'cos(x)');  % 图例
>> grid on;  % 显示网格

Octave绘制的正弦和余弦函数图，包含坐标轴标签、图例和网格

绘制多个子图：


>> x = 0:0.01:2*pi;
>> subplot(2, 1, 1);  % 2行1列的第1个子图
>> plot(x, sin(x));
>> title('sin(x)');
>> subplot(2, 1, 2);  % 2行1列的第2个子图
>> plot(x, cos(x));
>> title('cos(x)');

散点图和直方图：


>> x = randn(100, 1);  % 100个随机数
>> y = randn(100, 1);
>> scatter(x, y);  % 散点图
>> title('散点图');
 
>> figure;  % 新建图窗
>> hist(x, 20);  % 直方图，20个柱子
>> title('直方图');

三维图和等高线图：


>> x = -2:0.1:2;
>> y = -2:0.1:2;
>> [X, Y] = meshgrid(x, y);  % 创建网格
>> Z = X.^2 + Y.^2;  % 计算z值
 
>> figure;
>> surf(X, Y, Z);  % 三维曲面图
>> xlabel('x'); ylabel('y'); zlabel('z');
>> title('z = x^2 + y^2');
 
>> figure;
>> contour(X, Y, Z);  % 等高线图
>> colorbar;  % 显示颜色条

保存图片：


>> print -dpng 'my_plot.png'  % 保存为PNG文件
>> print -djpeg 'my_plot.jpg'  % 保存为JPEG文件

可视化在机器学习中非常重要。我们用它来探索数据分布，观察特征与标签的关系，展示模型的拟合效果，监控训练过程等。掌握基本的绘图技能，能大大提升我们的分析能力。

控制语句

虽然向量化编程是Octave的精髓，但有时我们仍需要控制流语句。

for循环：


>> for i = 1:5
     disp(i);
   end
   1
   2
   3
   4
   5
 
>> sum = 0;
>> for i = 1:10
     sum = sum + i;
   end
>> sum
sum = 55

while循环：


>> i = 1;
>> while i <= 5
     disp(i);
     i = i + 1;
   end
   1
   2
   3
   4
   5

if语句：


>> x = 5;
>> if x > 0
     disp('正数');
   elseif x < 0
     disp('负数');
   else
     disp('零');
   end
正数

break和continue：


>> for i = 1:10
     if i == 5
       break;  % 跳出循环
     end
     disp(i);
   end
   1
   2
   3
   4
 
>> for i = 1:5
     if mod(i, 2) == 0  % 如果是偶数
       continue;  % 跳过本次迭代
     end
     disp(i);
   end
   1
   3
   5

定义函数。函数可以写在单独的.m文件中：


% 文件名: myFunction.m
function y = myFunction(x)
  y = x^2 + 2*x + 1;
end

然后在命令行中调用：


>> myFunction(3)
ans = 16

多输出函数：


% 文件名: squared AndCubed.m
function [sq, cu] = squaredAndCubed(x)
  sq = x^2;
  cu = x^3;
end
 
>> [a, b] = squaredAndCubed(3)
a = 9
b = 27

虽然控制流语句很有用，但在Octave中应该尽量避免使用循环。向量化的代码不仅更简洁，运行速度也快得多（常常快几十到几百倍）。下一节我们会详细讨论向量化编程。

向量化编程：效率的关键

向量化编程是Octave/Matlab最重要的编程范式。它的核心思想是：用矩阵和向量运算代替循环，让底层的高度优化的线性代数库来处理计算。

让我们通过例子来理解。假设我们要计算 $h_\theta(x) = \theta^T x$ 对于所有训练样本。

非向量化的实现（不推荐）：


% X是mx(n+1)矩阵，theta是(n+1)x1向量
m = size(X, 1);
predictions = zeros(m, 1);
for i = 1:m
  predictions(i) = 0;
  for j = 1:size(X, 2)
    predictions(i) = predictions(i) + X(i, j) * theta(j);
  end
end

这段代码有两层循环，慢而且冗长。

向量化的实现（推荐）：


predictions = X * theta;

一行代码！不仅简洁，运行速度也快得多。当数据量大时，差异更明显。

再看一个例子：计算梯度 $\nabla J = \frac{1}{m} X^T (X\theta - y)$ 。

非向量化：


m = length(y);
n = size(X, 2);
gradient = zeros(n, 1);
for j = 1:n
  sum = 0;
  for i = 1:m
    sum = sum + (X(i,:) * theta - y(i)) * X(i, j);
  end
  gradient(j) = sum / m;
end

向量化：


gradient = (1/m) * X' * (X * theta - y);

向量化版本的优势显而易见。

让我们看一个完整的梯度下降实现：


function [theta, J_history] = gradientDescent(X, y, theta, alpha, numIter)
  m = length(y);
  J_history = zeros(numIter, 1);
  
  for iter = 1:numIter
    % 计算预测值（向量化）
    h = X * theta;
    
    % 计算误差（向量化）
    errors = h - y;
    
    % 计算梯度（向量化）
    gradient = (1/m) * X' * errors;
    
    % 更新参数（向量化）
    theta = theta - alpha * gradient;
    
    % 计算并记录代价函数（向量化）
    J_history(iter) = (1/(2*m)) * (errors' * errors);
  end
end

这个实现中，唯一的循环是迭代次数的循环，这是必要的。所有的数学运算都是向量化的。

向量化不仅适用于线性回归，它是所有机器学习算法高效实现的关键。神经网络的前向传播和反向传播、支持向量机的优化、K-means的聚类分配，都可以而且应该向量化实现。

向量化编程需要转变思维方式。不要想“对每个样本做什么”，而要想“对整个数据集做什么”。不要想循环和索引，而要想矩阵运算和广播。这需要练习，但一旦掌握，你会发现代码变得异常高效。


% 向量化思维的例子
 
% 任务：对向量的每个元素做sigmoid变换 sigmoid(x) = 1 / (1 + e^(-x))
 
% 非向量化（慢）
for i = 1:length(x)
  result(i) = 1 / (1 + exp(-x(i)));
end
 
% 向量化（快）
result = 1 ./ (1 + exp(-x));
 
% 注意使用了点除 ./ 和点减 -（减法不需要点，但exp需要作用到每个元素）

养成向量化编程的习惯。在写代码前，问自己：这个操作能不能用矩阵运算表达？如果能，就用向量化方式实现。只有在确实需要条件判断或动态决策时，才使用循环。

接下来

Octave/Matlab是强大的原型开发工具。虽然生产环境中我们可能用Python、C++等语言，但Octave非常适合快速实验想法、验证算法。很多研究论文的算法都先在Matlab中实现和测试，然后才移植到其他语言。

掌握Octave，你就拥有了一个高效的机器学习实验平台。下一部分我们将学习逻辑回归，这是我们遇到的第一个分类算法。我们会看到，逻辑回归虽然叫“回归”，实际上是用来做分类的，它是深度学习中神经网络的基础组件。

小练习

向量化计算sigmoid函数：编写Octave/Matlab代码，实现sigmoid函数的向量化版本。sigmoid函数定义为： $g(z) = \frac{1}{1 + e^{-z}}$

要求：
- 输入可以是标量、向量或矩阵
- 使用向量化运算，不使用循环
- 测试你的函数：sigmoid([-2, -1, 0, 1, 2])

答案：


function g = sigmoid(z)
  % SIGMOID 计算sigmoid函数
  % g = SIGMOID(z) 对z的每个元素计算sigmoid值
  
  g = 1 ./ (1 + exp(-z));
end

关键点说明：

使用点除 ./：这是元素级运算符，对矩阵的每个元素分别计算
exp(-z)：Octave会自动对z的每个元素计算指数
不需要循环：向量化运算自动处理各种尺寸的输入

测试示例：


% 测试1：向量输入
z = [-2, -1, 0, 1, 2];
g = sigmoid(z)
% 输出: [0.1192, 0.2689, 0.5000, 0.7311, 0.8808]
 
% 测试2：矩阵输入
Z = [0 1; 2 3];
G = sigmoid(Z)
% 输出: [0.5000 0.7311; 
%        0.8808 0.9526]
 
% 测试3：标量输入
g = sigmoid(0)
% 输出: 0.5000

性能对比：

非向量化版本（使用循环）：


function g = sigmoid_slow(z)
  g = zeros(size(z));
  for i = 1:numel(z)
    g(i) = 1 / (1 + exp(-z(i)));
  end
end

向量化版本快10-100倍！在z是大矩阵时差异更明显。

在机器学习中的应用：

逻辑回归的假设函数：h = sigmoid(X * theta)

实现向量化的梯度下降：使用Octave/Matlab实现线性回归的向量化梯度下降算法。

给定：
- 数据矩阵 X（m×n维，已包含偏置列）
- 标签向量 y（m×1维）
- 初始参数 theta（n×1维）
- 学习率 alpha
- 迭代次数 num_iters
编写函数 gradientDescent(X, y, theta, alpha, num_iters)，返回优化后的参数和代价函数历史。

答案：


function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
  % GRADIENTDESCENT 执行梯度下降来学习 theta
  % theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) 更新 theta
  
  % 初始化
  m = length(y);  % 训练样本数量
  J_history = zeros(num_iters, 1);  % 记录每次迭代的代价
  
  for iter = 1:num_iters
    % 向量化计算预测值
    h = X * theta;
    
    % 向量化计算误差
    errors = h - y;
    
    % 向量化计算梯度
    gradient = (1/m) * X' * errors;
    
    % 更新参数（同时更新所有参数）
    theta = theta - alpha * gradient;
    
    % 计算并保存当前代价
    J_history(iter) = (1/(2*m)) * (errors' * errors);
  end
end

完整的测试代码：


% 生成测试数据
m = 100;  % 样本数
X = [ones(m, 1), rand(m, 1) * 10];  % 添加偏置列
y = 3 + 2 * X(:,2) + randn(m, 1) * 0.5;  % y = 3 + 2x + 噪声
 
% 初始化参数
theta = zeros(2, 1);
alpha = 0.01;
num_iters = 1000;
 
% 运行梯度下降
[theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters);

Octave/Matlab教程 - 数值计算工具 | 自在学