神经网络表示

到目前为止，我们学习的算法——线性回归和逻辑回归——都是基于线性模型的。虽然通过特征工程（如添加多项式特征），我们可以用这些模型处理非线性关系，但当问题变得复杂时，需要的特征数量会急剧增长，计算和存储都会成为瓶颈。

神经网络（Neural Networks）为我们提供了一种更优雅的方式来处理复杂的非线性关系。神经网络可以自动学习特征的组合和变换，无需人工设计大量的多项式特征。这使得神经网络在图像识别、语音识别、自然语言处理等领域取得了突破性的成功。

这一部分我们将学习神经网络的基本结构，理解神经元和网络层的概念，掌握前向传播算法。我们会发现，神经网络其实是逻辑回归的自然扩展，它的基本组件就是我们已经熟悉的sigmoid函数。

为什么需要非线性假设

让我们先理解为什么线性模型（即使加上多项式特征）在某些问题上不够用。考虑一个图像识别问题：识别一张50x50像素的灰度图片中是否包含汽车。

这张图片有50x50=2500个像素，每个像素是一个特征，所以我们有2500个输入特征。如果我们想用逻辑回归加上二次多项式特征，需要构造所有的二次项 $x_i x_j$。二次项的数量大约是 $\frac{2500 \times 2500}{2} \approx 3$ 百万个！这是一个巨大的数字。

如果考虑三次多项式，特征数量会更加庞大。训练这样的模型不仅计算量巨大，而且极易过拟合——特征数量远超样本数量。

但人类的视觉系统能够轻松识别图片中的物体。我们的大脑是如何做到的？神经科学研究表明，大脑通过层层处理视觉信息：底层神经元检测边缘和简单图案，中层神经元组合这些简单特征检测复杂图案，高层神经元识别完整的物体。每一层都在前一层的基础上构建更抽象的表示。

神经网络受到这种生物学启发。它通过多层计算，从原始输入逐步提取更高级的特征，最终做出决策。关键是，网络会自动学习每一层应该提取什么特征，而不需要人工设计。

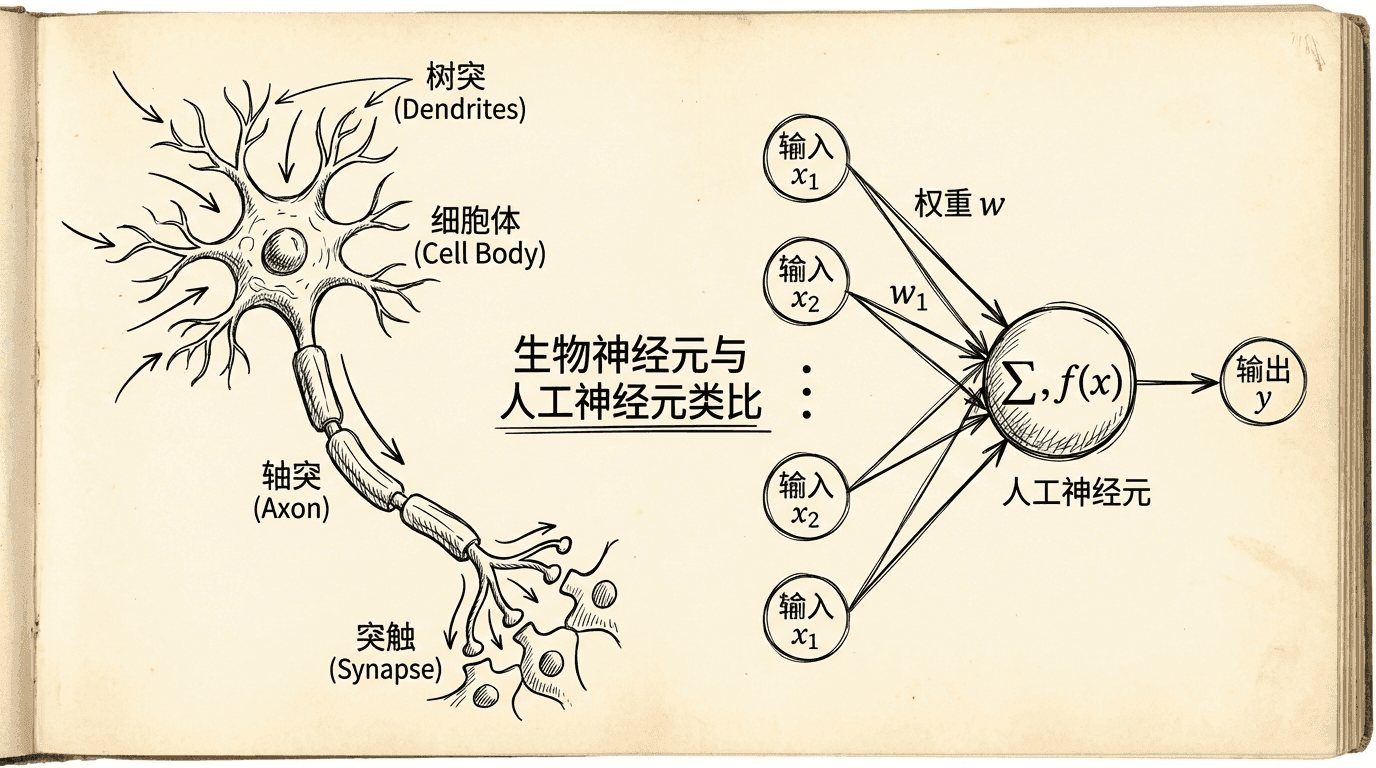
神经元：网络的基本单元

人工神经元是神经网络的基本组件。它模拟了生物神经元的行为：接收多个输入，进行加权求和，然后通过一个非线性函数产生输出。

一个神经元可以这样表示：

$a = g(\theta^T x) = g(\theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 + ... + \theta_n x_n)$

这里：

• $x_0, x_1, ..., x_n$ 是输入特征（$x_0 = 1$ 是偏置项）

看起来很熟悉对吧？这就是逻辑回归！一个神经元就是一个逻辑回归单元。

在神经网络的术语中：

• 输入层（Input Layer）：接收原始特征
• 隐藏层（Hidden Layers）：中间的计算层
• 输出层（Output Layer）：产生最终预测
• 激活值（Activation）：每个神经元的输出

神经网络的结构与前向传播

一个简单的神经网络由多层神经元组成。最简单的结构是三层网络：

• 输入层：包含 $n$ 个输入特征 $x_1, x_2, ..., x_n$（加上偏置 $$）

让我们看一个具体的例子。假设输入层有3个特征（加上偏置共4个），隐藏层有3个神经元，输出层有1个神经元（二分类问题）。

用符号表示：

• $a_i^{(j)}$ 表示第 $j$ 层的第 $i$ 个神经元的激活值
• $\Theta^{(j)}$ 表示从第 层到第 层的权重矩阵

前向传播（Forward Propagation）的过程：

步骤1：输入层

$a^{(1)} = x = \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{bmatrix}$

步骤2：计算隐藏层

对于隐藏层的每个神经元：

$z_1^{(2)} = \Theta_{10}^{(1)} x_0 + \Theta_{11}^{(1)} x_1 + \Theta_{12}^{(1)} x_2 + \Theta_{13}^{(1)} x_3$

类似地计算 $a_2^{(2)}$ 和 $a_3^{(2)}$。用矩阵表示：

$z^{(2)} = \Theta^{(1)} a^{(1)}$ $a^{(2)} = g(z^{(2)})$

别忘了添加偏置单元 $a_0^{(2)} = 1$。

步骤3：计算输出层

$z^{(3)} = \Theta^{(2)} a^{(2)}$ $a^{(3)} = g(z^{(3)})$

$a^{(3)}$ 就是网络的最终输出，即预测值 $h_\Theta(x)$。

隐藏层的每个神经元都在计算输入的某种特征。这些特征是自动学习的，不需要人工设计。输出层则基于这些学到的特征做出最终决策。

向量化实现非常简洁：

|
def sigmoid(z):
    return 1 / (1 + np.exp(-z))
 
def forwardProp(X, Theta1, Theta2):
    """
    X: 输入矩阵 (m x (n+1))，每行一个样本
    Theta1: 输入层到隐藏层的权重 (h x (n+1))
    Theta2: 隐藏层到输出层的权重 (k x (h+1))
    返回: 输出层的激活值
    """
    m = X.shape[0]
    
    # 第一层（输入层）
    a1 = X  # m x (n+1)
    
    # 第二层（隐藏层）
    z2 

上述几行代码，完整地实现了一个标准前馈神经网络（含单隐藏层）的前向传播过程。通过高效的矩阵运算（向量化实现），网络能够同时处理多个训练样本，自动完成各层的加权求和、激活函数计算、以及偏置的引入。 在隐藏层与输出层的非线性变换中，利用sigmoid函数赋予网络拟合复杂非线性函数的能力。如此紧凑的向量化代码，不仅极大提升了计算效率，还避免了显式的循环写法，是现代神经网络实现的基本规范之一。 这种向量化思想对于深度学习框架（如TensorFlow、PyTorch）底层高性能实现至关重要。

通过例子理解神经网络

神经网络能够表达复杂的函数。让我们通过一些简单的例子来建立直觉。

例子1：逻辑与（AND）

考虑一个最简单的神经网络：2个输入，1个输出，没有隐藏层。如果我们想让它实现逻辑与运算：当 $x_1 = 1$ 且 $x_2 = 1$ 时输出1，否则输出0。

可以设置权重为 $\theta = [-30, 20, 20]$。则：

$h_\Theta(x) = g(-30 + 20x_1 + 20x_2)$

• 当 $x_1 = 0, x_2 = 0$：$h = g(-30) \approx 0$

完美地实现了AND！

例子2：逻辑或（OR）

类似地，用 $\theta = [-10, 20, 20]$ 可以实现OR运算。

例子3：逻辑非（NOT）

用 $\theta = [10, -20]$ 可以实现NOT运算。

例子4：异或（XOR）

有趣的是，单个神经元（没有隐藏层）无法实现XOR运算——XOR不是线性可分的。但使用一个隐藏层就可以了！

我们可以这样构造：

• 隐藏层第一个神经元实现 $x_1 \text{ AND } x_2$
• 隐藏层第二个神经元实现 $x_1 \text{ OR } x_2$

这正是XOR的定义！这个例子说明，即使一个很小的神经网络（一个隐藏层），也能表达单层网络无法表达的函数。

多类分类

对于多分类问题（比如识别手写数字0-9），输出层需要有多个神经元，每个对应一个类别。

假设有K个类别，输出层有K个神经元。对于类别 $k$，我们的目标输出是：

$y^{(k)} = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 1 \\ \vdots \\ 0 \end{bmatrix} \leftarrow \text{第k个位置是1，其他是0}$

这种表示方式称为独热编码（One-Hot Encoding）。

网络的输出 $h_\Theta(x)$ 也是一个K维向量，每个元素表示对应类别的概率：

$h_\Theta(x) = \begin{bmatrix} P(y=1|x;\Theta) \\ P(y=2|x;\Theta) \\ \vdots \\ P(y=K|x;\Theta) \end{bmatrix}$

预测时，我们选择概率最大的类别：$\hat{y} = \arg\max_k h_\Theta(x)_k$。

代码示例：

|
def predictMulticlass(X, Theta1, Theta2):
    """
    多分类预测
    返回每个样本最可能的类别
    """
    # 前向传播得到所有类别的概率
    probs = forwardProp(X, Theta1, Theta2)  # m x K
    
    # 选择概率最大的类别
    predictions = np.argmax(probs, axis=1)
    
    return predictions

神经网络的层次化特征学习

神经网络最令人兴奋的特性是它能够自动学习层次化的特征表示。在图像识别中：

第一层（接近输入）：学习检测简单的边缘、颜色块等低级特征。每个神经元对输入的某种简单模式敏感。

第二层：组合第一层的特征，检测更复杂的图案，如角点、简单形状。

第三层：检测物体的部分，如眼睛、轮子、窗户。

输出层：基于高层特征识别完整的物体，如人脸、汽车、房子。

这种层次化的表示非常强大。底层的特征（如边缘检测器）可以被不同的高层特征共享。比如“竖直边缘检测器”既可以用于识别人（检测身体轮廓），也可以用于识别建筑（检测墙壁）。这种特征共享使得网络能够高效地学习。

在实践中，我们很少手动设定神经网络的权重。相反，我们用训练数据和学习算法让网络自己学习权重。接下来我们将学习如何训练神经网络——这需要一个称为反向传播的算法，它是梯度下降在神经网络上的应用。

小练习

1. 手动计算神经网络前向传播：给定一个简单的神经网络，手动计算其输出。

   网络结构：

   • 输入层：2个输入 $x_1 = 0.5, x_2 = 0.3$
   • 隐藏层：2个神经元
   • 输出层：1个神经元

   权重矩阵： ${\mathrm{\Theta }}^{(1)}=[\begin{array}{ccc}0.1& 0.2& 0.3\\ \end{array}$

2. 设计一个XOR神经网络：XOR（异或）是一个非线性问题，无法用单个逻辑回归解决。设计一个两层神经网络来解决XOR问题。

   XOR真值表：

   $x_1$	$x_2$	$y$
   0	0	0
   0	1	1
   1	0	1
   1	1	0

   提示：可以将XOR分解为：$y=(x_1$

激活函数使用sigmoid：$g(z) = \frac{1}{1+e^{-z}}$

计算网络的输出。

步骤2：计算隐藏层的输入（加权和）

$z^{(2)} = \Theta^{(1)} a^{(1)} = \begin{bmatrix} 0.1 & 0.2 & 0.3 \\ 0.4 & 0.5 & 0.6 \end{bmatrix} \begin{bmatrix} 1 \\ 0.5 \\ 0.3 \end{bmatrix}$

第1个隐藏神经元： $z_1^{(2)} = 0.1 \times 1 + 0.2 \times 0.5 + 0.3 \times 0.3 = 0.1 + 0.1 + 0.09 = 0.29$

第2个隐藏神经元： $z_2^{(2)} = 0.4 \times 1 + 0.5 \times 0.5 + 0.6 \times 0.3 = 0.4 + 0.25 + 0.18 = 0.83$

步骤3：应用激活函数

$a_1^{(2)} = g(z_1^{(2)}) = g(0.29) = \frac{1}{1+e^{-0.29}} \approx \frac{1}{1+0.748} \approx 0.572$

$a_2^{(2)} = g(z_2^{(2)}) = g(0.83) = \frac{1}{1+e^{-0.83}} \approx \frac{1}{1+0.436} \approx 0.696$

隐藏层输出（加上偏置）： $a^{(2)} = \begin{bmatrix} 1 \\ 0.572 \\ 0.696 \end{bmatrix}$

步骤4：计算输出层的输入

$z^{(3)} = \Theta^{(2)} a^{(2)} = \begin{bmatrix} 0.7 & 0.8 & 0.9 \end{bmatrix} \begin{bmatrix} 1 \\ 0.572 \\ 0.696 \end{bmatrix}$

$z^{(3)} = 0.7 \times 1 + 0.8 \times 0.572 + 0.9 \times 0.696 = 0.7 + 0.458 + 0.626 = 1.784$

步骤5：计算最终输出

$a^{(3)} = g(z^{(3)}) = g(1.784) = \frac{1}{1+e^{-1.784}} \approx \frac{1}{1+0.168} \approx 0.856$

最终输出：约 0.856

Python验证：

理解前向传播：

• 每一层的计算都是：加权和 → 激活函数
• 偏置单元在每层都要添加（除了输出层）
• 信息从输入层流向输出层，逐层计算
• 这个过程就是神经网络的"预测"过程

权重设置：

第一层权重 $\Theta^{(1)}$（连接输入层到隐藏层）： $\Theta^{(1)} = \begin{bmatrix} -30 & 20 & -20 \\ -30 & -20 & 20 \end{bmatrix}$

• 第1行：$z_1 = -30 + 20x_1 - 20x_2$ （AND NOT门）
• 第2行：$z_2 = -30 - 20x_1 + 20x_2$ （AND NOT门）

第二层权重 $\Theta^{(2)}$（连接隐藏层到输出层）： $\Theta^{(2)} = \begin{bmatrix} -10 & 20 & 20 \end{bmatrix}$

• $z_3 = -10 + 20a_1 + 20a_2$ （OR门）

验证：

输入 (0, 0)：

• $z_1 = -30 + 0 - 0 = -30$ → $a_1 = g(-30) \approx 0$
• $z_2 = -30 - 0 + 0 = -30$ → $a_2 = g(-30) \approx 0$
• $z_3 = -10 + 0 + 0 = -10$ → $a_3 = g(-10) \approx 0$ ✓

输入 (0, 1)：

• $z_1 = -30 + 0 - 20 = -50$ → $a_1 = g(-50) \approx 0$
• $z_2 = -30 - 0 + 20 = -10$ → $a_2 = g(-10) \approx 0$

等等，让我用更合理的权重：

更简单的权重方案：

$\Theta^{(1)} = \begin{bmatrix} -10 & 20 & 20 \\ -30 & 20 & 20 \end{bmatrix}$

$\Theta^{(2)} = \begin{bmatrix} -10 & 20 & -20 \end{bmatrix}$

Python实现和验证：

关键启示：

1. XOR是非线性问题，需要至少一个隐藏层
2. 神经网络通过组合简单的非线性单元来学习复杂模式
3. 隐藏层的每个神经元可以学习输入空间的不同区域
4. 两层神经网络可以表示任何布尔函数
5. 这就是神经网络强大表达能力的根源！