神经网络反向传播与计算图

在上一节中，我们学习了神经网络的前向传播：给定输入 $\vec{x}$ 和参数 $\theta = \{W^{(1)}, \vec{b}^{(1)}, W^{(2)}, \vec{b}^{(2)}, \ldots\}$，计算输出 $\vec{y}$ 和损失 $\mathcal{L}$。

现在我们面临的核心问题是：如何计算损失函数对所有参数的梯度？

只有计算出梯度，才能使用梯度下降等优化算法更新参数。

朴素的做法是对每个参数独立计算梯度——用数值微分，每次改变一个参数的值，重新前向传播计算损失的变化。但这需要对每个参数进行一次完整的前向传播。对于包含数百万参数的深度网络，这意味着数百万次前向传播，完全不可行。

反向传播算法优雅地解决了这个问题：通过一次前向传播和一次反向传播，就能高效计算所有参数的梯度。关键洞察是利用链式法则，让梯度从输出层反向流向输入层，每层的梯度可以用上一层的梯度计算出来，无需重复前向传播。更妙的是，反向传播的时间复杂度与前向传播相当——都是$O(W)$，其中$W$是参数数量。这使得训练深度网络成为可能，是现代深度学习的基石。

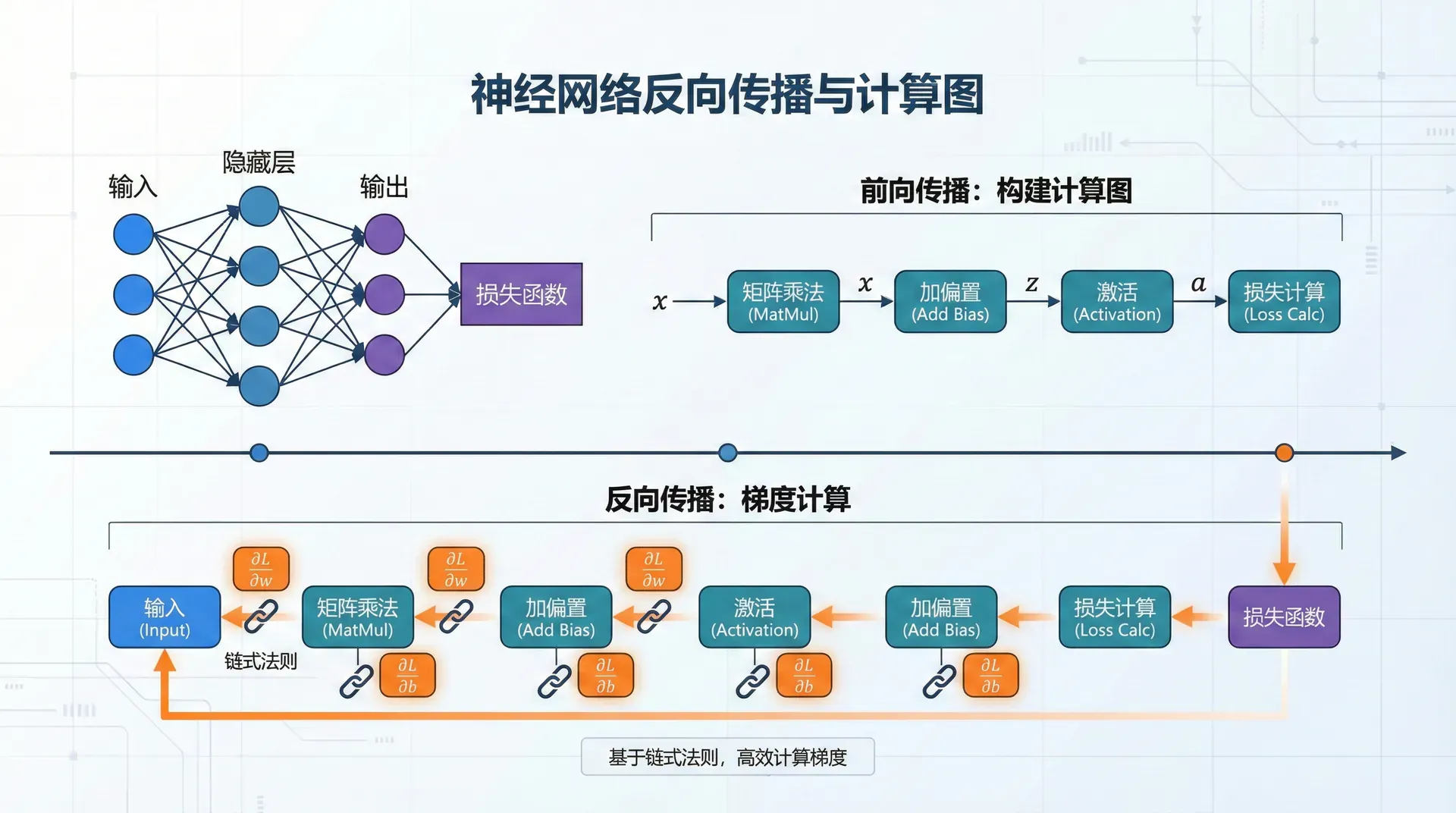
反向传播（Backpropagation）的数学基础是微积分中的链式法则（Chain Rule）——复合函数的导数等于各部分导数的乘积。但将链式法则从标量推广到向量、矩阵，并应用到深度神经网络中，需要精妙的数学推导和工程实现。

这节课我们将带你从最基本的链式法则开始，逐步理解如何在多层网络中反向传播梯度。我们会用计算图（Computational Graph） 这个强大的工具来可视化计算过程——前向传播时构建图，反向传播时沿着图反向传递梯度。这不仅帮助理解算法，更是现代深度学习框架（如PyTorch）的核心机制。

我们还将学习矩阵求导的技巧——如何高效地计算损失对权重矩阵的梯度，如何避免维度不匹配的错误，如何用向量化的代码替代慢速的循环。最后，我们会深入PyTorch的自动微分机制，理解loss.backward()这一行代码背后发生的魔法。

链式法则

链式法则是微积分的基本定理，也是反向传播的数学基础。

标量链式法则

单变量链式法则

对于复合函数 $f(g(x))$，导数为：

示例：设 $f(g) = g^2$，$g(x) = x + 1$，求 $\frac{df}{dx}$

多变量链式法则

对于 $z = f(x, y)$，其中 $x = x(t)$，$y = y(t)$：

|
    t
   / \
  x   y
   \ /
    z

梯度从 $z$ 沿两条路径回传到 $t$，最后相加。

深层复合函数

对于 $y = f_n(f_{n-1}(\cdots f_2(f_1(x)) \cdots))$：

这正是深度神经网络中梯度的传播方式。

向量链式法则

设 $f: \mathbb{R}^n \rightarrow \mathbb{R}$，即 $f$ 是多元函数。其梯度是一个向量：

约定：梯度是列向量，与 $\vec{x}$ 的形状相同。

设 $\vec{f}: \mathbb{R}^n \rightarrow \mathbb{R}^m$，即 $$。其雅可比矩阵为：

重要性质：雅可比矩阵的第 $i$ 行是 $\nabla_{\vec{x}} f_i$。

对于 $\vec{z} = \vec{f}(\vec{y})$ 和 ：

即雅可比矩阵的乘积：$J_{\vec{z}}(\vec{x}) = J_{\vec{z}}(\vec{y}) \cdot J_{\vec{y}}(\vec{x})$

让我们验证维度的一致性。如果$\vec{z} \in \mathbb{R}^p$，$\vec{y} \in \mathbb{R}^m$，，那么雅可比矩阵的维度是（输出维度×输入维度），的维度是。两个雅可比矩阵相乘，得到，正好是应有的维度。这个维度一致性检查是实现反向传播时避免bug的重要技巧。

反向模式微分

在神经网络中，我们最终关心的是标量损失 $\mathcal{L}$ 对所有参数的梯度。

在自动微分中，有两种基本模式：前向模式和反向模式。

前向模式从输入开始，逐层计算雅可比矩阵。我们依次计算$\frac{\partial \vec{h}^{(1)}}{\partial \vec{x}}$，，...最终通过链式法则得到。但这需要存储每一层的雅可比矩阵——如果输入是1000维，隐藏层也是1000维，那么雅可比矩阵就是，占用巨大内存。

反向模式则从输出开始，逐层回传梯度。我们先计算$\frac{\partial \mathcal{L}}{\partial \vec{h}^{(L)}}$（最后一层的梯度），然后用它计算，依此类推。关键是，每一步我们只需要存储一个与变量同形的梯度向量——1000维变量对应1000维梯度，而非的雅可比矩阵。

这个差异至关重要。对于神经网络，损失是标量（单个数字），但参数可能有数百万维。前向模式需要存储$1 \times 10^6$的雅可比矩阵（虽然一维，但仍需逐个计算），而反向模式只需要存储$10^6$维梯度向量。反向模式在空间和时间效率上都远胜前向模式——这就是为什么我们用反向传播训练神经网络。

计算图

计算图将复杂的数学表达式分解为简单的原子操作，使得反向传播的实现和理解变得直观。

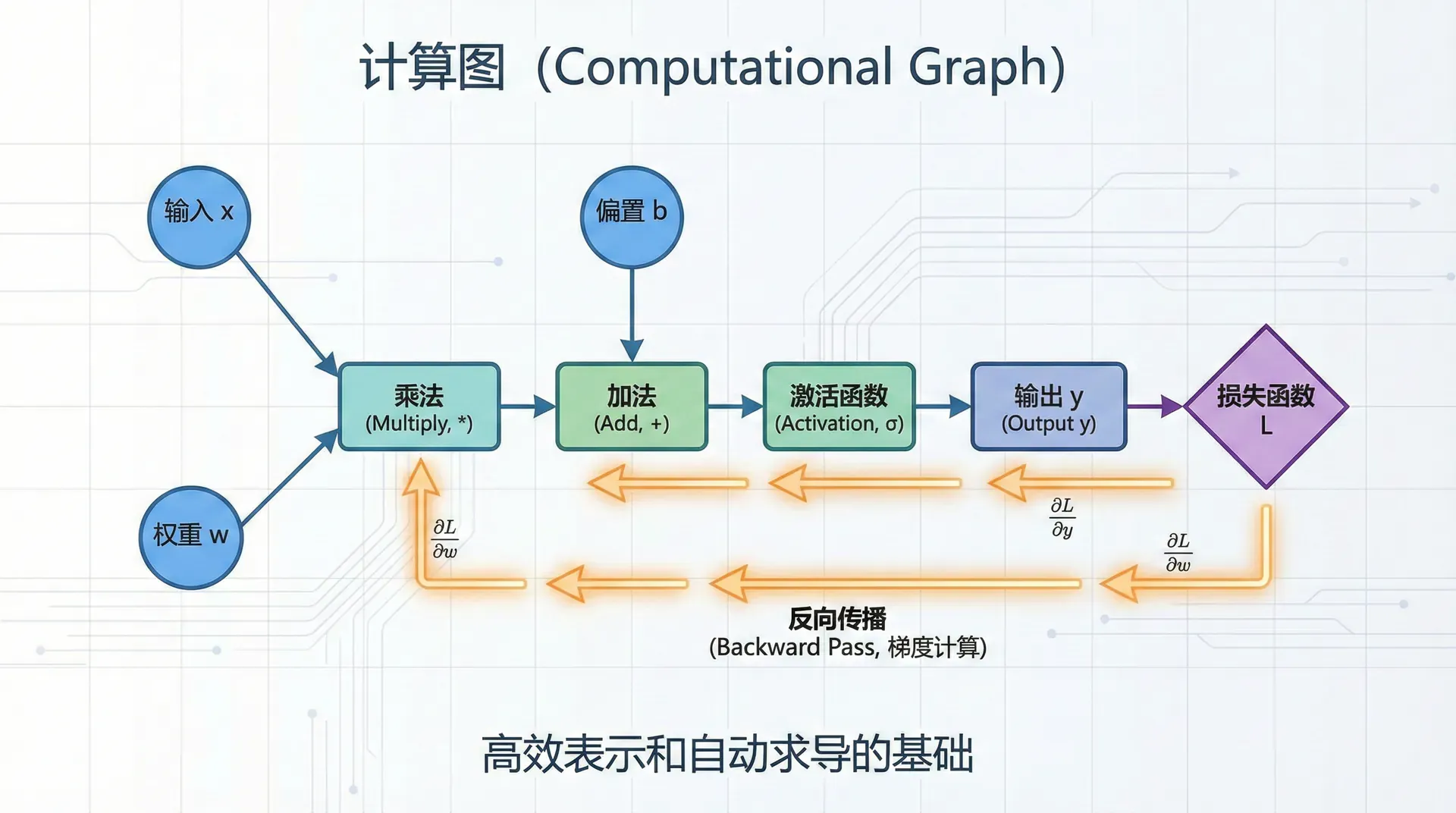
计算图（Computational Graph） 是可视化和理解神经网络计算的强大工具。它是一个有向无环图（DAG），节点表示变量（如输入、权重、激活值、损失），边表示数据如何流动——从输入流向输出，从层与层之间传递。

计算图有两种表示风格。在操作节点风格中，节点是操作（如加法、乘法、ReLU），边是变量。在变量节点风格中，节点是变量，边是操作。本讲主要使用变量节点风格，因为它更直观地展示了梯度如何沿着变量反向传播。无论哪种风格，核心思想都是一样的：前向传播时沿着图的方向计算，反向传播时沿着相反方向传递梯度。

简单示例

表达式：$f(x, y, z) = (x + y) \cdot z$

计算图：

|
x   y
 \ /
  +  (a = x + y)
  |
  *  z
  |
  f  (f = a * z)

让我们用具体数值走一遍。在前向传播中，给定输入$x = -2$，$y = 5$，$z = -4$，我们先计算中间值$a = x + y = 3$，然后计算输出。这一步很直接，就是按照公式计算。

反向传播的目标是计算$\frac{\partial f}{\partial x}$，$\frac{\partial f}{\partial y}$，——每个输入变量对输出的影响。这就是我们需要的梯度，用于参数更新。

从输出开始：

回传到 $a$ 和 $z$（乘法门）：

回传到 $x$ 和 $y$（加法门）：

门的类型与梯度分配

加法门

局部梯度：

反向传播：

直观理解：加法门将上游梯度原样分发给所有输入。

乘法门

局部梯度：

反向传播：

直观理解：乘法门将上游梯度乘以另一个输入的值。

MAX门

局部梯度：

反向传播：将上游梯度路由给前向传播时值较大的输入。

分支与梯度累加

如果一个变量被多次使用（分支），其梯度是所有分支梯度之和。

示例：$z = x \cdot x = x^2$

计算图：

|
    x
   / \
  *   *
   \ /
    z

反向传播：

这与直接求导的结果一致：$\frac{d(x^2)}{dx} = 2x$。

神经网络的计算图

两层神经网络示例：

计算图：

|
x → [W^(1), b^(1)] → z^(1) → ReLU → h → [W^(2), b^(2)] → o → Loss

反向传播按相反方向计算梯度：

|
∂L/∂L=1 → ∂L/∂o → ∂L/∂W^(2), ∂L/∂b^(2) → ∂L/∂h → ∂L/∂z^(1) → ∂L/∂W^(1), ∂L/∂b^(1)

反向传播算法

算法框架

|
算法：反向传播
输入：训练样本 (x, y), 网络参数 θ
输出：损失 L, 梯度 ∇θ L
 
# 前向传播
1. 初始化 a^(0) = x
2. for l = 1 to L:
3.     z^(l) = W^(l) a^(l-1) + b^(l)
4.     a^(l) = f^(l)(z^(l))
5.     缓存 z^(l), a^(l)  # 后续计算梯度需要
6. 计算损失 L = Loss(a^(L), y)
 
# 反向传播
7. 初始化输出梯度 ∂L/∂a^(L) = ∇_{a^(L)} Loss
8. for l = L downto 1:
9.     # 反向传播通过激活函数
10.    ∂L/∂z^(l) = ∂L/∂a^(l) ⊙ f'^(l)(z^(l))
11.    
12.    # 计算权重和偏置的梯度
13.    ∂L/∂W^(l) = ∂L/∂z^(l) (a^(l-1))^T
14.    ∂L/∂b^(l) = ∂L/∂z^(l)
15.    
16.    # 反向传播到前一层
17.    if l > 1:
18.        ∂L/∂a^(l-1) = (W^(l))^T ∂L/∂z^(l)
 
19. 返回 L, {∂L/∂W^(l), ∂L/∂b^(l)}

符号说明：

• $\odot$：逐元素乘法（Hadamard product）
• $f'^{(l)}(z^{(l)})$：激活函数的导数，逐元素计算

关键步骤推导

输出层梯度

对于交叉熵损失和softmax输出：

梯度：

这是一个优美的结果：梯度就是预测概率减去真实标签。

推导：需要结合softmax和交叉熵的导数。

反向传播通过线性层

给定：

已知 $\frac{\partial \mathcal{L}}{\partial \vec{z}}$，求 $\frac{\partial \mathcal{L}}{\partial W}$，，。

偏置的梯度（最简单）：

因为 $\frac{\partial z_i}{\partial b_i} = 1$。

权重的梯度：

方法1：逐元素推导

用矩阵形式：

维度验证：

• $\frac{\partial \mathcal{L}}{\partial W} \in \mathbb{R}^{m \times n}$（与 $W$ 形状相同）
• $\frac{}{}$（列向量）

输入的梯度：

推导：

这正是矩阵乘法 $W^T \frac{\partial \mathcal{L}}{\partial \vec{z}}$ 的第 个分量。

反向传播通过激活函数

给定 $\vec{a} = f(\vec{z})$，已知 $$，求 。

对于逐元素激活函数（如ReLU、sigmoid、tanh）：

向量形式：

常见激活函数的导数：

ReLU的反向传播：

实现技巧：前向传播时缓存 $z_i > 0$ 的布尔掩码，反向传播时直接使用。

完整示例：两层神经网络

网络定义：

前向传播：

|
# 输入：x (n, ), y (m, )
z1 = W1 @ x + b1  # (d, )
h = np.maximum(0, z1)  # ReLU, (d, )
o = W2 @ h + b2  # (m, )
loss = 0.5 * np.sum((o - y) ** 2)

反向传播：

|
# 输出层梯度
dL_do = o - y  # (m, )
 
# 第二层参数梯度
dL_dW2 = np.outer(dL_do, h)  # (m, d)
dL_db2 = dL_do  # (m, )
 
# 传播到h
dL_dh = W2.T @ dL_do  # (d, )
 
# 通过ReLU
dL_dz1 = dL_dh * (z1 > 0)  # (d, )
 
# 第一层参数梯度
dL_dW1 = np.outer(dL_dz1, x)  

矩阵求导技巧

形状约定

金科玉律：梯度的形状必须与原变量的形状完全相同。

• 若 $W \in \mathbb{R}^{m \times n}$，则 $\frac{\partial \mathcal{L}}{\partial W} \in \mathbb{R}^{m \times n}$

这个约定使得梯度更新变得直观：

矩阵求导公式

以下是常用的矩阵求导公式（假设 $\mathcal{L}$ 是标量）：

1. 线性变换：

2. 二次型：

如果 $A$ 是对称的，则 $\frac{\partial \mathcal{L}}{\partial \vec{x}} = 2A\vec{x}$

3. 迹的梯度：

雅可比矩阵的实用技巧

当面对复杂的矩阵求导时，可以采用以下策略：

策略1：逐元素推导

1. 先推导单个元素的偏导数 $\frac{\partial \mathcal{L}}{\partial W_{ij}}$
2. 识别索引模式
3. 整理成矩阵形式

策略2：维度分析

1. 确定梯度的目标形状
2. 用已知的梯度和变量拼凑出正确的形状
3. 验证是否符合链式法则

策略3：使用微分

从损失的微分推导出梯度矩阵。

自动微分与PyTorch

自动微分的类型

数值微分：使用有限差分近似

缺点：

• 计算量大（每个参数需要额外的前向传播）
• 数值不稳定（$h$ 的选择很关键）

符号微分：使用符号计算系统（如Mathematica）推导导数的解析表达式

缺点：

• 表达式可能非常复杂
• 不适合程序化实现

自动微分：通过链式法则自动计算梯度

• 前向模式：从输入到输出计算导数
• 反向模式：从输出到输入计算梯度（即反向传播）

优势：

• 精确（不是数值近似）
• 高效（与前向传播同量级）
• 易于实现

PyTorch的autograd机制

PyTorch使用动态计算图和反向模式自动微分。

基本使用

|
import torch
 
# 创建张量，设置requires_grad=True
x = torch.tensor([2.0], requires_grad=True)
y = torch.tensor([3.0], requires_grad=True)
 
# 定义计算
z = x ** 2 + y ** 3
loss = z.sum()
 
# 反向传播
loss.backward()
 
# 访问梯度
print

梯度累积与清零

默认情况下，.backward() 会累积梯度：

|
x = torch.tensor([1.0], requires_grad=True)
 
for i in range(3):
    y = x ** 2
    y.backward()
    print(f"Iteration {i+1}, grad: {x.grad}")
 
# 输出：
# Iteration 1, grad: tensor([2.])
# Iteration 2, grad: tensor([4.])  # 累积

梯度清零：

|
x.grad.zero_()  # 或 optimizer.zero_grad()

计算图与叶子节点

|
x = torch.tensor([1.0], requires_grad=True)  # 叶子节点
y = x + 2                                     # 非叶子节点
z = y * y
z.backward()
 
print(x.grad)  # ✓ 可以访问
# print(y.grad)  # ✗ 非叶子节点的梯度会被释放

保留中间梯度：

|
y.retain_grad()
z.backward()
print(y.grad)  # ✓ 现在可以访问

detach与no_grad

detach：从计算图中分离

|
x = torch.tensor([1.0], requires_grad=True)
y = x ** 2
z = y.detach()  # z不再是计算图的一部分
w = z * 3
w.backward()  # 错误！z是叶子节点且requires_grad=False

no_grad：临时禁用梯度计算

|
with torch.no_grad():
    y = x ** 2  # 不会构建计算图

用于推理阶段，节省内存和计算。

自定义反向传播

有时我们需要自定义操作的反向传播：

|
class MyReLU(torch.autograd.Function):
    @staticmethod
    def forward(ctx, input):
        """前向传播"""
        ctx.save_for_backward(input)
        return input.clamp(min=0)
    
    @staticmethod
    def backward(ctx, grad_output):
        """反向传播"""
        input, = ctx.saved_tensors
        grad_input 

用途：

• 实现自定义层
• 优化特定操作的反向传播
• 实现数值稳定的梯度计算

实践与调试

梯度检查（Gradient Checking）

梯度检查用于验证反向传播实现的正确性。

方法：使用数值梯度近似

其中 $e_i$ 是第 $i$ 个坐标的单位向量，$\epsilon$ 通常取 $10^{-4}$ 到 $10^{-7}$。

实现：

|
def gradient_check(f, x, analytic_grad, eps=1e-5):
    """
    检查解析梯度是否正确
    
    Args:
        f: 函数，返回标量
        x: 输入点
        analytic_grad: 解析梯度
        eps: 数值微分步长
    
    Returns:
        相对误差
    """
    # 数值梯度
    numeric_grad = np.zeros_like(x)
    for i in range(x.size):
        x_plus = x.copy()
        x_plus.flat[i] += eps
        x_minus 

注意事项：

• 梯度检查很慢，仅用于调试
• 对于随机层（如Dropout），需要禁用随机性
• 使用双精度浮点数提高精度

常见错误与调试

错误1：形状不匹配

|
# 错误
grad_W = grad_z.T @ a  # 转置错误
 
# 正确
grad_W = grad_z @ a.T  # 外积

调试方法：打印所有张量的形状，验证维度一致性。

错误2：忘记梯度清零

|
# 错误
for epoch in epochs:
    loss.backward()  # 梯度累积！
    optimizer.step()
 
# 正确
for epoch in epochs:
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

错误3：就地操作破坏计算图

|
# 错误
x += 1  # 就地操作
 
# 正确
x = x + 1  # 创建新张量

练习与思考

1. 解释为什么反向传播的时间复杂度与前向传播相当，而不是指数级。

2. 在计算图中，如果一个变量被多次使用（分支），其梯度如何计算？为什么？

3. 为什么在PyTorch中需要调用 .zero_grad()？如果忘记调用会发生什么？

4. 解释前向模式自动微分和反向模式自动微分的区别，为什么神经网络使用反向模式？

5. 推导softmax函数与交叉熵损失的组合梯度：

证明：

6. 对于批量归一化层：

推导 $\frac{\partial \mathcal{L}}{\partial x_i}$，$\frac{\partial \mathcal{L}}{\partial \gamma}$，。

7. 推导sigmoid函数梯度的简洁形式：

8. 手动实现一个两层神经网络的前向传播和反向传播（不使用自动微分）：

|
class TwoLayerNet:
    def __init__(self, input_dim, hidden_dim, output_dim):
        # 初始化权重
        pass
    
    def forward(self, X):
        # 前向传播
        pass
    
    def backward(self, dL_dout):
        # 反向传播
        pass

9. 使用梯度检查验证你的实现是否正确。

10. 实现一个自定义的 LeakyReLU 层，包括前向传播和反向传播：

|
class LeakyReLU(torch.nn.Module):
    def __init__(self, alpha=0.01):
        super().__init__()
        self.alpha = alpha
    
    def forward(self, x):
        # 你的实现
        pass

使用PyTorch的autograd验证你的实现。

小结

本节课我们系统梳理了反向传播算法的核心思想和实现方法。我们从链式法则出发，讲解了如何用计算图将复杂的梯度计算分解为局部操作，从而高效地计算神经网络所有参数的梯度，并结合矩阵求导和自动微分原理，说明了现代深度学习框架能够自动完成梯度推导和参数更新的原因。 反向传播的本质，是利用链式法则，将前向传播过程中缓存的中间结果用于梯度回传，实现高效可靠的训练。掌握反向传播之后，我们就具备了实现各类深度学习模型的数学和工程基础。