机器翻译、seq2seq与注意力机制 - 序列到序列模型 | 自在学
机器翻译、seq2seq与注意力机制
机器翻译可能是人工智能最古老的梦想之一。1954年,Georgetown-IBM实验首次展示了计算机自动将俄语翻译成英语,当时的研究者乐观地预测,三到五年内机器翻译问题就能解决。
然而,现实远比想象复杂——语言的歧义性、文化差异、习语表达,让机器翻译成为一个持续了半个多世纪的挑战。
从基于规则的系统(需要语言学家手工编写数千条翻译规则),到统计机器翻译(通过海量双语语料学习翻译概率),再到2014年神经机器翻译的横空出世,机器翻译经历了多次范式转变。
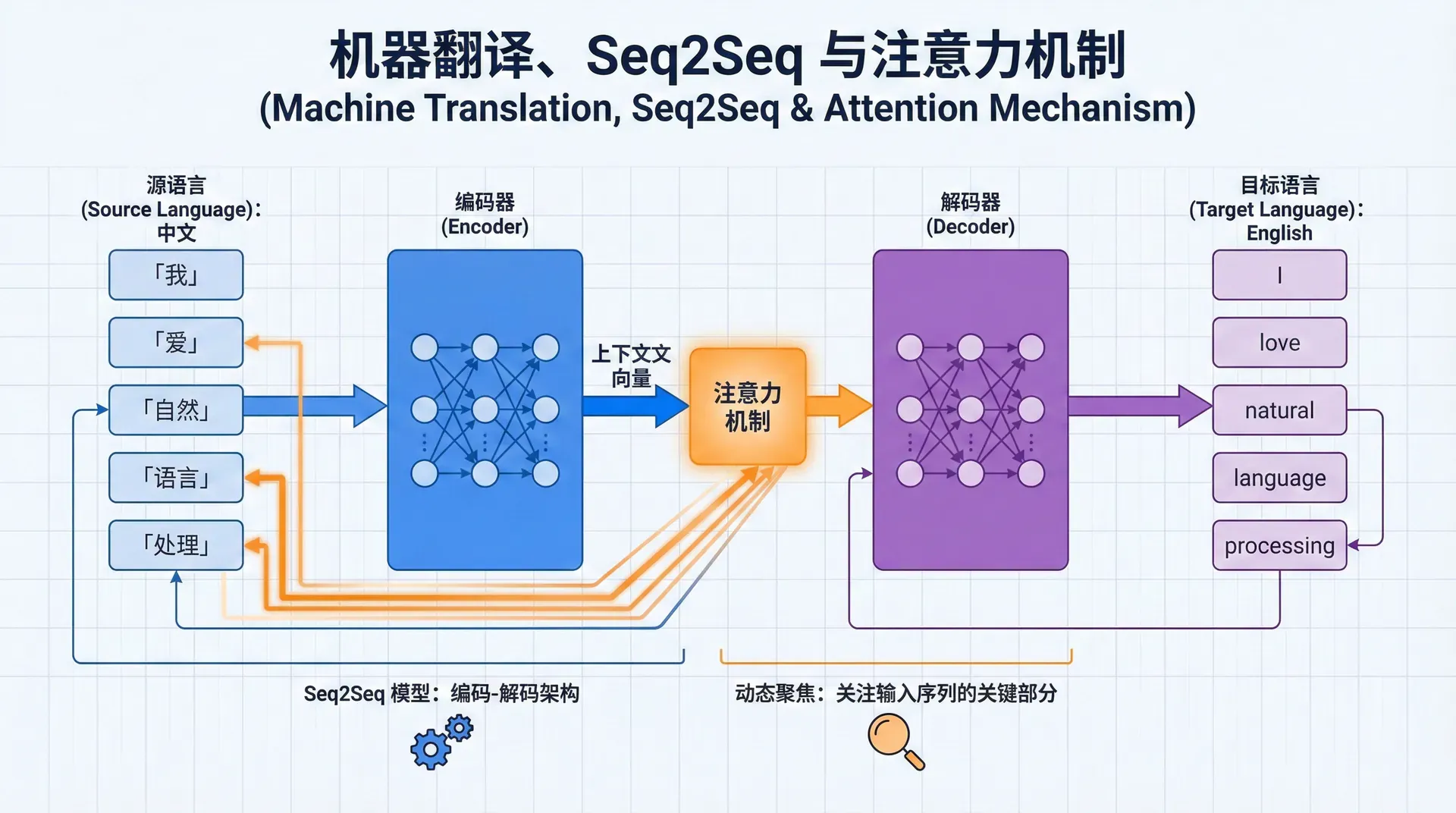
而序列到序列(Sequence-to-Sequence, seq2seq) 模型的提出,标志着端到端神经翻译时代的开启。
更重要的是,seq2seq不只是一个翻译模型——它是一个通用的序列转换框架。文本摘要、对话生成、语音识别、代码生成,所有这些“输入一个序列,输出另一个序列”的任务,都可以用seq2seq建模。本讲将深入理解seq2seq的设计、它的根本局限,以及注意力机制如何优雅地解决这些局限。
seq2seq模型:编码器-解码器的诞生
2014年,两篇几乎同时出现的论文奠定了seq2seq的基础:Sutskever等人(Google)的“Sequence to Sequence Learning with Neural Networks”和Cho等人的“Learning Phrase Representations using RNN Encoder-Decoder”。
两篇论文提出了相似的架构,核心思想极其简洁:用一个RNN编码源句子,用另一个RNN解码生成目标句子 。
编码器:将句子压缩为向量
编码器是一个标准的RNN(通常是LSTM),逐词处理源语言句子:
h ⃗ t enc = LSTM ( x ⃗ t , h ⃗ t − 1 enc ) \vec{h}_t^{\text{enc}} = \text{LSTM}(\vec{x}_t, \vec{h}_{t-1}^{\text{enc}}) h t enc = LSTM ( x t , h 其中x ⃗ t \vec{x}_t x t t t t h ⃗ T enc \vec{h}_T^{\text{enc}}
这个设计蕴含了一个大胆的假设:一个固定长度的向量(通常是512或1024维)足以捕获任意长句子的所有信息 。无论源句子是5个词还是50个词,都要压缩到相同维度的向量中。这个向量承载了句子的含义、语法结构、主题等所有信息——就像把一本书的精华浓缩成一段摘要。
解码器:从向量展开为句子
解码器也是一个RNN,但它的任务是生成目标语言句子。解码器的初始隐藏状态由编码器的最终状态初始化:
s ⃗ 0 = h ⃗ T enc \vec{s}_0 = \vec{h}_T^{\text{enc}} s 0 = h 然后,解码器自回归地生成目标词。在每个时间步t t t
s ⃗ t = LSTM ( y ⃗ t − 1 , s ⃗ t − 1 ) \vec{s}_t = \text{LSTM}(\vec{y}_{t-1}, \vec{s}_{t-1}) s t = LSTM ( y P ( y t ∣ y < t , x ⃗ ) = softmax ( W s ⃗ t ) P(y_t | y_{<t}, \vec{x}) = \text{softmax}(W \vec{s}_t) P ( y t ∣ y < t , x 其中y ⃗ t − 1 \vec{y}_{t-1} y t − 1 s ⃗ t \vec{s}_t s
这个生成过程是自回归的——每个词的生成依赖于之前已生成的词。就像写作一样,我们一个词接一个词地构建句子,每个新词都基于前文的语境。
训练:教师强制的双刃剑
seq2seq模型的训练使用**教师强制(Teacher Forcing)**策略。在计算s ⃗ t \vec{s}_t s t y t − 1 y_{t-1} y t − 1
for t in range ( 1 , T_target): # 使用真实词 y[t-1] s_t = decoder(y[t - 1 ], s_{t - 1 }) output = softmax(W @ s_t) loss += cross_entropy(output, y[t]) 教师强制极大地加速了训练。因为每一步都使用正确的输入,模型可以快速学习在"正确轨道"上的下一步预测。而且,所有时间步可以并行计算(在训练时我们已经知道完整的目标序列),这充分利用了GPU的并行能力。
然而,教师强制也带来了问题——暴露偏差(Exposure Bias) 。训练时模型总是看到正确的历史,但测试时必须依赖自己的预测。如果早期生成了错误的词,后续的输入分布就与训练时不同,模型可能不知所措。这就像总是在理想环境下练车的新手,第一次上真实道路时会手忙脚乱。
解码:寻找最优翻译
测试时,我们需要从所有可能的目标序列中找到概率最高的那个:
y ⃗ ∗ = arg max y ⃗ P ( y ⃗ ∣ x ⃗ ) \vec{y}^* = \arg\max_{\vec{y}} P(\vec{y} | \vec{x}) y ∗ = arg 贪婪解码 是最简单的策略——每步选择概率最高的词。但我们在第15讲中已经知道,贪婪解码的短视可能导致次优结果。
**束搜索(Beam Search)**在机器翻译中几乎是标准配置。维护k = 5 k=5 k = 5 k = 10 k=10 k = 10 k k k
信息瓶颈
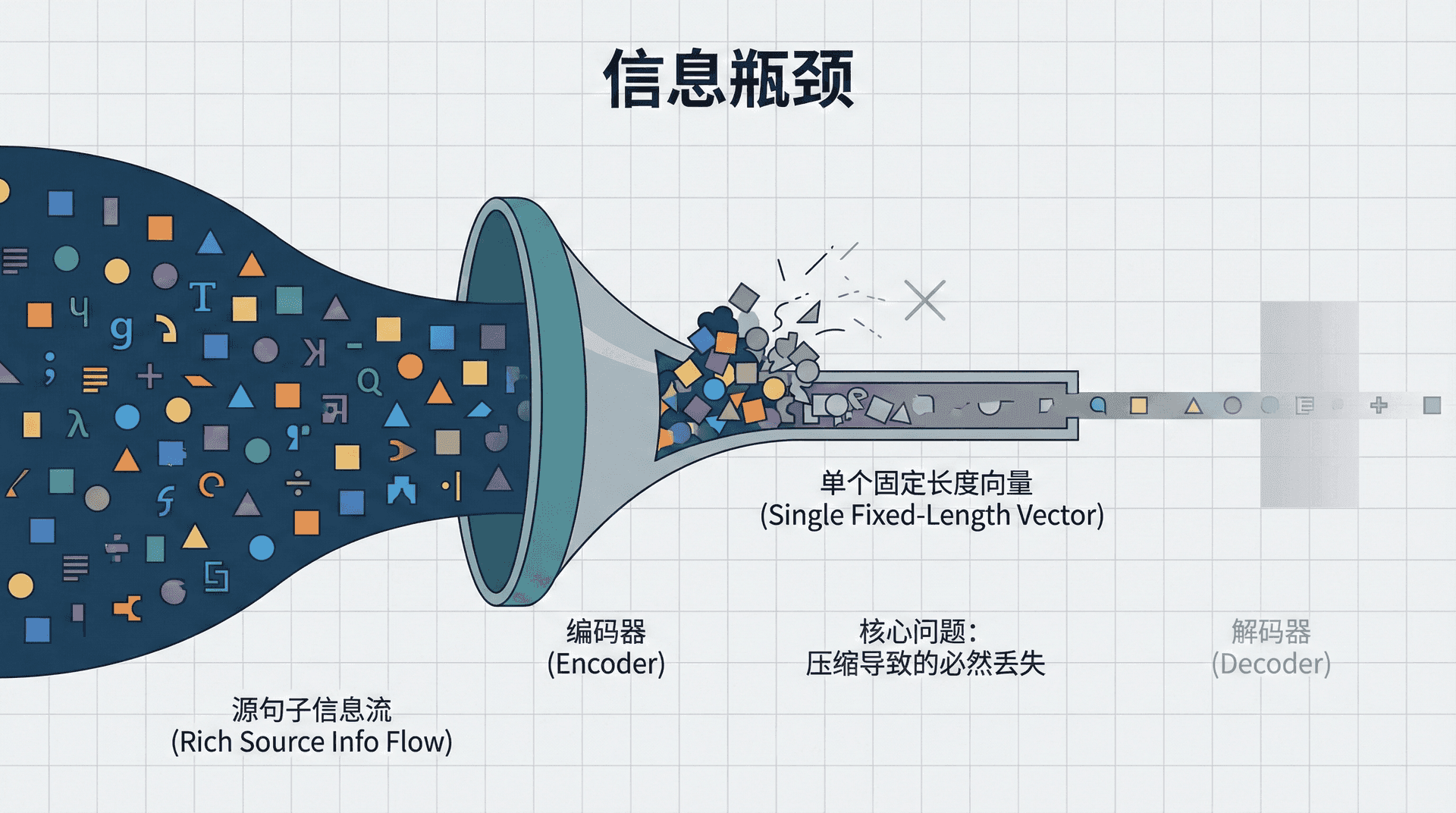
seq2seq模型在2014年取得了令人振奋的结果,在某些任务上甚至接近人类翻译质量。然而,研究者们很快发现了一个根本性的问题:将整个源句子压缩到单个固定长度向量,信息必然会丢失 。
瓶颈的数学分析
考虑翻译一个50词的英文句子到中文。编码器处理50个词后,必须将所有信息——每个词的含义、词与词的关系、整体的语法结构、句子的主题——全部塞进一个512维的向量中。
从信息论角度看,这是一个有损压缩 过程。源句子包含的信息量远超512个实数所能编码的。必然有一些信息会在压缩过程中丢失,尤其是:
早期词的信息:RNN的遗忘特性使得句首的词对最终状态影响较小
罕见词和专有名词:这些词的微妙含义可能被泛化掉
词序信息:虽然RNN编码了序列,但在最终向量中词序信息可能模糊
实验证据
Cho等人(2014)在分析seq2seq性能时发现了一个明显的模式:翻译质量随源句子长度下降 。短句子(10-20词)翻译质量接近人类;但当句子超过30词时,BLEU分数显著下降;到40-50词,翻译常常出现漏译、错译、语序混乱。
这个现象直接指向信息瓶颈问题。短句子的信息量小,可以合理地压缩到固定向量;但长句子的信息溢出了向量的表达能力,导致信息丢失。
具体的失败案例很能说明问题。翻译句子“The agreement on the European Economic Area was signed in August 1992”时,基础seq2seq可能生成“欧洲经济区协议签署于...”,丢失了时间信息“1992年8月”。这是因为编码器在处理句子时,后面的“August 1992”覆盖了前面的“agreement”和“European Economic Area”的部分信息,导致解码器在生成中文时遗漏关键细节。
人类翻译的启示
观察人类如何翻译,会发现我们并不是先理解整个句子,压缩到脑海中的一个“思想”,然后再展开成目标语言 。相反,我们是逐段翻译——在翻译“European Economic Area”时,重点关注源文本中的这几个词;在翻译“August 1992”时,回头看源文本中的时间信息。
人类翻译过程是一个动态对齐 的过程:在生成目标语言的每个部分时,有选择地关注源语言的相关部分。这正是注意力机制要模拟的——不要强迫编码器将所有信息压缩到单一向量,而是让解码器在需要时直接查阅源句子的不同部分。
注意力机制
2015年,Bahdanau等人发表了题为“Neural Machine Translation by Jointly Learning to Align and Translate”的论文。这篇论文提出的注意力机制(Attention Mechanism)从根本上改变了seq2seq的设计,解决了信息瓶颈问题,并为后续的Transformer奠定了基础。
动态查询
注意力机制的核心思想极其简单却强大:让解码器在每一步都能“回头看”编码器的所有隐藏状态,并动态决定关注哪些部分 。
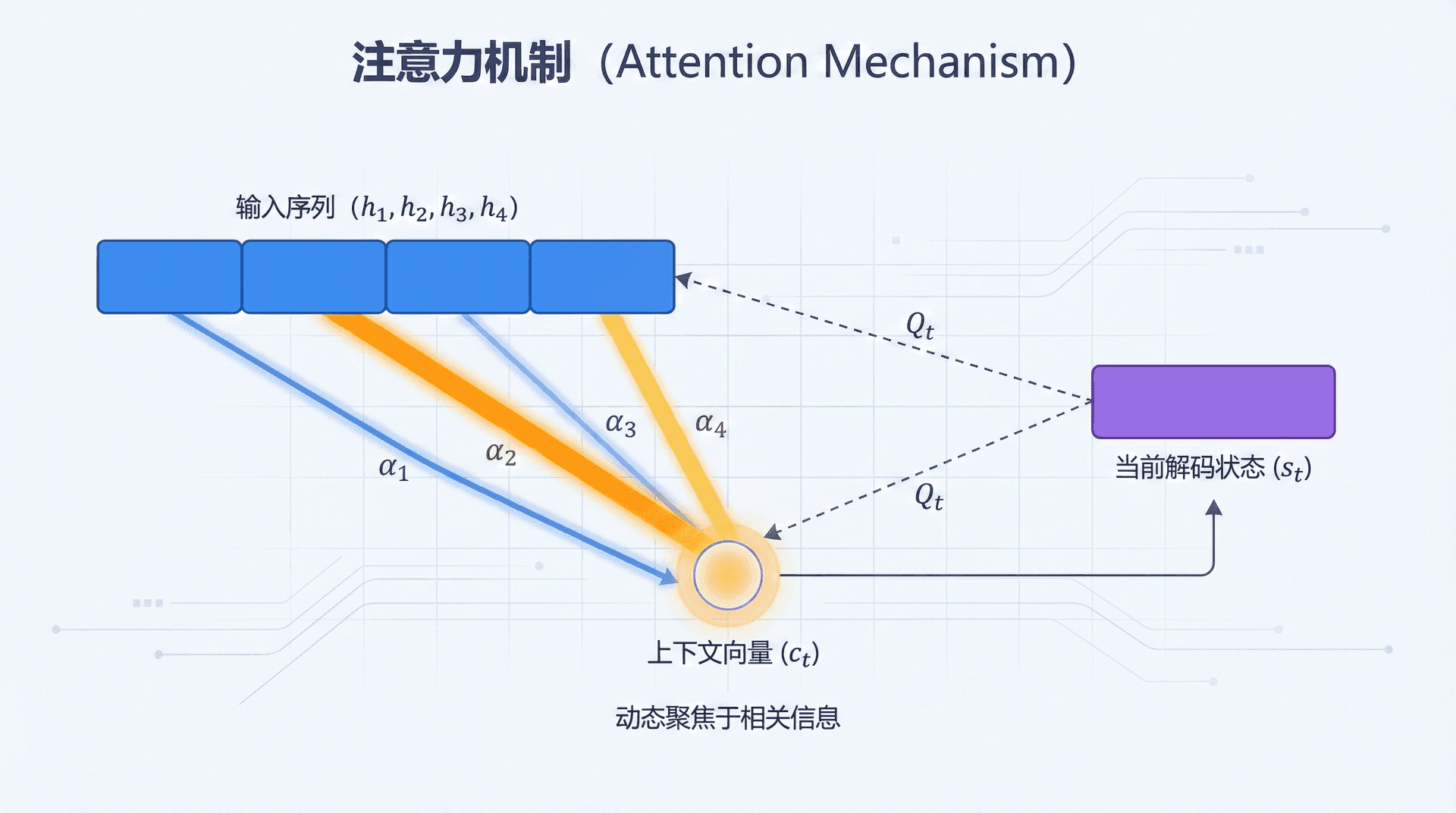
不再有单一的上下文向量c ⃗ \vec{c} c t t t c ⃗ t \vec{c}_t c
c ⃗ t = ∑ i = 1 T src α t , i h ⃗ i enc \vec{c}_t = \sum_{i=1}^{T_{\text{src}}} \alpha_{t,i} \vec{h}_i^{\text{enc}} c t = i = 1 其中α t , i \alpha_{t,i} α t , i t t t i i i
让我们用一个具体例子理解。翻译“我爱自然语言处理” → “I love natural language processing”:
生成“I”时 :
注意力主要集中在“我”(权重α 1 , 1 ≈ 0.8 \alpha_{1,1} \approx 0.8 α 1 , 1 ≈ 0.8
对其他词关注较少
上下文向量c ⃗ 1 ≈ 0.8 h ⃗ 1 + 0.1 h ⃗ 2 + … \vec{c}_1 \approx 0.8 \vec{h}_1 + 0.1 \vec{h}_2 + \ldots c
生成“natural language processing”时 :
注意力集中在“自然语言处理”(α 3 , 3 ≈ 0.7 \alpha_{3,3} \approx 0.7 α 3 , 3 ≈ 0.7
上下文向量c ⃗ 3 \vec{c}_3 c
通过这种动态注意力,解码器可以在每一步获取最相关的源语言信息,不受固定向量大小的限制。
注意力的数学机制
注意力机制包含三个步骤:
第一步:计算相关性分数
对于解码器当前状态s ⃗ t − 1 \vec{s}_{t-1} s t − 1 h ⃗ i \vec{h}_i h
e t , i = score ( s ⃗ t − 1 , h ⃗ i ) e_{t,i} = \text{score}(\vec{s}_{t-1}, \vec{h}_i) e t , i = score ( s 这个分数衡量"当前解码状态与源词i i i i i i
score函数有多种选择 :
加性注意力(Bahdanau Attention) :
score ( s ⃗ , h ⃗ ) = v ⃗ T tanh ( W 1 s ⃗ + W 2 h ⃗ ) \text{score}(\vec{s}, \vec{h}) = \vec{v}^T \tanh(W_1 \vec{s} + W_2 \vec{h}) score ( s , h 这是Bahdanau等人在2015年提出的原始版本。两个状态先通过各自的线性变换,然后相加,经tanh \tanh tanh v ⃗ \vec{v} v W 1 W_1 W 1 W 2 W_2
乘性注意力(Luong Attention) :
score ( s ⃗ , h ⃗ ) = s ⃗ T W h ⃗ \text{score}(\vec{s}, \vec{h}) = \vec{s}^T W \vec{h} score ( s , h ) 这是Luong等人几个月后提出的简化版本。两个状态通过一个双线性形式结合,计算更高效。
点积注意力(Dot-product) :
score ( s ⃗ , h ⃗ ) = s ⃗ T h ⃗ \text{score}(\vec{s}, \vec{h}) = \vec{s}^T \vec{h} score ( s , h ) 最简单的版本——直接计算两个向量的点积。要求编码器和解码器维度相同。这个方法在Transformer中被采纳(加上了缩放因子1 / d 1/\sqrt{d} 1/ d
实践中,这几种方法性能差异不大。加性注意力参数更多(W 1 , W 2 , v ⃗ W_1, W_2, \vec{v} W 1 , W 2 , v
第二步:归一化为概率分布
将所有分数通过softmax归一化:
α t , i = exp ( e t , i ) ∑ j = 1 T src exp ( e t , j ) \alpha_{t,i} = \frac{\exp(e_{t,i})}{\sum_{j=1}^{T_{\text{src}}} \exp(e_{t,j})} α t , i = ∑ j = 1 现在α t , 1 , … , α t , T src \alpha_{t,1}, \ldots, \alpha_{t,T_{\text{src}}} α t , 1 , … , α t , T src
第三步:计算上下文向量
用注意力权重对所有编码器状态加权求和:
c ⃗ t = ∑ i = 1 T src α t , i h ⃗ i enc \vec{c}_t = \sum_{i=1}^{T_{\text{src}}} \alpha_{t,i} \vec{h}_i^{\text{enc}} c t = i = 1 这个上下文向量c ⃗ t \vec{c}_t c t
第四步:融入解码
上下文向量与解码器状态结合,用于预测当前词:
s ⃗ t = LSTM ( [ y ⃗ t − 1 ; c ⃗ t ] , s ⃗ t − 1 ) \vec{s}_t = \text{LSTM}([\vec{y}_{t-1}; \vec{c}_t], \vec{s}_{t-1}) s t = LSTM ([ P ( y t ∣ y < t , x ⃗ ) = softmax ( W [ s ⃗ t ; c ⃗ t ] ) P(y_t | y_{<t}, \vec{x}) = \text{softmax}(W[\vec{s}_t; \vec{c}_t]) P ( y t ∣ y < t , x 注意我们将上下文向量c ⃗ t \vec{c}_t c t
注意力的直观理解
注意力机制可以用多个类比来理解:
图书馆类比 :编码器把源句子的每个词存入"图书馆"的不同书架。解码器在生成每个词时,向图书馆"查询"相关信息——查询词汇书架来翻译名词,查询语法书架来确定词序。注意力权重决定了在每个书架前停留多长时间。
软索引类比 :传统的索引(如数组)是硬的——array[3]只返回位置3的元素。注意力是软索引——它返回所有位置的加权组合,权重反映了相关性。这种软索引是可微的,可以通过反向传播学习。
记忆网络类比 :编码器将源句子存入"外部记忆",每个词占一个记忆槽。解码器有一个"读取头",可以通过生成查询向量,从记忆中读取相关内容。这与现代的Memory Network和Neural Turing Machine的思想一脉相承。
注意力权重的可视化
注意力机制的一个美妙特性是可解释性 。我们可以将注意力权重矩阵{ α t , i } \{\alpha_{t,i}\} { α t , i }
在英中翻译"The cat sat on the mat" → "猫坐在垫子上"时,注意力权重矩阵通常会显示:
生成"猫"时,"cat"的权重最高
生成"坐"时,"sat"的权重最高
生成"垫子"时,"mat"和"the"的权重都较高
这种对齐(alignment)不是人工标注的,而是模型自动学习的。在训练过程中,模型发现"当我要生成'猫'时,关注源语言中的'cat'能得到更低的loss",于是逐渐学会了正确的对齐。
对于语序差异大的语言对(如英语和日语),注意力权重显示出更复杂的模式——可能是对角线的反转、多对一或一对多的对齐。这些模式反映了两种语言之间的结构差异,是纯统计学习的结果,令人惊叹。
注意力机制的深层意义
注意力机制的重要性远超解决seq2seq的信息瓶颈。它引入了几个深刻的思想,影响了后续整个深度学习领域的发展。
软选择 vs 硬选择
传统编程中,我们通过索引、指针等方式“硬”选择数据。注意力机制是软选择(Soft Selection) ——不是二元的选或不选,而是给每个候选一个0到1之间的权重,然后加权组合。
软选择的优势在于可微性。因为所有操作都是连续的(加权求和、softmax),梯度可以流过整个注意力机制。模型可以通过反向传播学习正确的注意力模式,无需显式监督。
内容寻址
注意力机制实现了基于内容的寻址(Content-based Addressing) 。传统的寻址是基于位置的(给我第3个元素),注意力是基于内容的(给我与当前查询最相关的元素)。
这个思想后来被扩展到记忆增强神经网络(如Neural Turing Machine, Differentiable Neural Computer),这些模型用注意力机制访问外部记忆,实现了类似计算机的读写操作,但完全可微、可端到端学习。
从局部到全局
注意力机制还代表了从局部感知野到全局感知野 的转变。RNN和CNN都是局部的——RNN每次只看一个新词,CNN的卷积核只看一个小窗口。要获得全局信息,需要堆叠多层。
注意力让每个位置可以一步直接"看到"所有其他位置。这为Transformer的完全注意力架构(放弃RNN和CNN)铺平了道路——既然我们可以用注意力直接建模任意位置对的关系,为什么还需要循环或卷积?
PyTorch完整实现
让我们实现一个带注意力的seq2seq模型。这个实现集成了我们讨论的所有组件:
import torch import torch.nn as nn import torch.nn.functional as F
class Encoder ( nn . Module ): """seq2seq编码器(使用双向LSTM)""" def __init__ (self, vocab_size, embed_size, hidden_size, num_layers = 1 , dropout = 0.3 ): super (Encoder, self ). __init__ () self .hidden_size = 这个实现包含了现代seq2seq的所有关键组件:双向LSTM编码器、Bahdanau注意力、单向LSTM解码器、教师强制训练、贪婪解码生成。代码可以直接用于训练翻译模型。
注意力机制的影响
性能提升
Bahdanau等人在2015年报告,在WMT英法翻译任务上,带注意力的seq2seq使BLEU分数从之前的最佳28.5提升到34.8——这是巨大的进步。更重要的是,性能不再随句子长度显著下降 。50词的句子翻译质量与20词的句子相当,因为注意力机制缓解了信息瓶颈。
对齐的自动学习
注意力机制自动学习了源语言和目标语言之间的对齐关系。在统计机器翻译时代,对齐(alignment)需要用专门的模型(如IBM Model)学习,是一个独立的复杂步骤。注意力将对齐整合到端到端训练中,无需显式监督就学会了对齐。
启发后续研究
注意力机制的成功启发了NLP之外的领域:
图像描述(Image Captioning) :在生成描述时关注图像的不同区域视觉问答 :根据问题动态关注图像的相关部分阅读理解 :在回答问题时关注文章的相关段落Transformer (2017):完全基于注意力,放弃了RNN
可以说,注意力机制是过去十年深度学习最重要的创新之一。
练习与思考
用一个具体的翻译例子(自己构造),说明seq2seq的信息瓶颈问题如何导致翻译质量下降。
推导注意力机制中上下文向量c ⃗ t \vec{c}_t c t h ⃗ i \vec{h}_i h
t − 1
enc
)
h
T enc
上下文向量(context vector)或 思想向量(thought vector)
T enc
t − 1
,
)
)
=
t
y ^ t − 1 \hat{y}_{t-1} y ^ t − 1 max
P
(
∣
)
t
∑
T src
α t , i
1
≈
…
3
i
t − 1
,
)
)
=
W 2
=
=
T src
exp
(
e t , j
)
exp ( e t , i )
t t t
∑
T src
α t , i
y
t − 1
;
]
,
)
)
=
hidden_size
self .num_layers = num_layers
# 词嵌入
self .embedding = nn.Embedding(vocab_size, embed_size)
self .dropout = nn.Dropout(dropout)
# 双向LSTM编码器
# 双向能同时捕获左右上下文,对理解源句子很有帮助
self .lstm = nn.LSTM(
embed_size, hidden_size, num_layers,
batch_first = True ,
bidirectional = True ,
dropout = dropout if num_layers > 1 else 0
)
def forward (self, src):
"""
Args:
src: (batch, src_len) 源语言词ID
Returns:
outputs: (batch, src_len, 2*hidden) 所有时刻的隐藏状态
hidden: (2*num_layers, batch, hidden) 最终隐藏状态
"""
# 词嵌入
embedded = self .dropout( self .embedding(src))
# 通过双向LSTM
outputs, hidden = self .lstm(embedded)
# outputs: 每个时刻的前向+后向隐藏状态拼接
# hidden: (h_n, c_n),各为(2*num_layers, batch, hidden)
return outputs, hidden
class BahdanauAttention ( nn . Module ):
"""Bahdanau加性注意力"""
def __init__ (self, enc_hidden_size, dec_hidden_size):
super (BahdanauAttention, self ). __init__ ()
# 编码器隐藏状态投影
self .W_encoder = nn.Linear( 2 * enc_hidden_size, dec_hidden_size, bias = False )
# 解码器隐藏状态投影
self .W_decoder = nn.Linear(dec_hidden_size, dec_hidden_size, bias = False )
# 能量函数的输出投影
self .V = nn.Linear(dec_hidden_size, 1 , bias = False )
def forward (self, decoder_hidden, encoder_outputs):
"""
计算注意力权重和上下文向量
Args:
decoder_hidden: (batch, dec_hidden) 解码器当前隐藏状态
encoder_outputs: (batch, src_len, 2*enc_hidden) 编码器所有隐藏状态
Returns:
context: (batch, 2*enc_hidden) 上下文向量
attention_weights: (batch, src_len) 注意力权重
"""
batch_size, src_len, _ = encoder_outputs.shape
# 扩展解码器隐藏状态以匹配源长度
# (batch, dec_hidden) -> (batch, src_len, dec_hidden)
decoder_hidden = decoder_hidden.unsqueeze( 1 ).repeat( 1 , src_len, 1 )
# 计算能量分数
# tanh(W_dec * s + W_enc * h)
energy = torch.tanh(
self .W_decoder(decoder_hidden) + self .W_encoder(encoder_outputs)
) # (batch, src_len, dec_hidden)
# 通过V投影到标量
attention_scores = self .V(energy).squeeze( 2 ) # (batch, src_len)
# Softmax归一化为概率分布
attention_weights = F.softmax(attention_scores, dim = 1 )
# 加权求和编码器状态得到上下文向量
# (batch, 1, src_len) @ (batch, src_len, 2*enc_hidden) = (batch, 1, 2*enc_hidden)
context = torch.bmm(attention_weights.unsqueeze( 1 ), encoder_outputs)
context = context.squeeze( 1 ) # (batch, 2*enc_hidden)
return context, attention_weights
class Decoder ( nn . Module ):
"""带注意力的解码器"""
def __init__ (self, vocab_size, embed_size, enc_hidden_size, dec_hidden_size,
num_layers = 1 , dropout = 0.3 ):
super (Decoder, self ). __init__ ()
self .dec_hidden_size = dec_hidden_size
self .num_layers = num_layers
# 词嵌入
self .embedding = nn.Embedding(vocab_size, embed_size)
self .dropout = nn.Dropout(dropout)
# 注意力层
self .attention = BahdanauAttention(enc_hidden_size, dec_hidden_size)
# LSTM解码器
# 输入:目标词嵌入 + 上下文向量
self .lstm = nn.LSTM(
embed_size + 2 * enc_hidden_size,
dec_hidden_size,
num_layers,
batch_first = True ,
dropout = dropout if num_layers > 1 else 0
)
# 输出层
# 输入:解码器隐藏状态 + 上下文向量
self .fc = nn.Linear(dec_hidden_size + 2 * enc_hidden_size, vocab_size)
def forward (self, input_token, hidden, encoder_outputs):
"""
解码一个时间步
Args:
input_token: (batch,) 当前输入词ID
hidden: (h, c),各为(num_layers, batch, dec_hidden)
encoder_outputs: (batch, src_len, 2*enc_hidden)
Returns:
output: (batch, vocab_size) 词概率分布
hidden: 更新后的隐藏状态
attention_weights: (batch, src_len) 注意力权重
"""
# 词嵌入
embedded = self .dropout( self .embedding(input_token)) # (batch, embed)
embedded = embedded.unsqueeze( 1 ) # (batch, 1, embed)
# 计算注意力
# 使用上一步的隐藏状态(h的最后一层)
h_prev = hidden[ 0 ][ - 1 ] # (batch, dec_hidden)
context, attention_weights = self .attention(h_prev, encoder_outputs)
# 拼接嵌入和上下文
lstm_input = torch.cat([embedded, context.unsqueeze( 1 )], dim = 2 )
# lstm_input: (batch, 1, embed + 2*enc_hidden)
# 通过LSTM
lstm_output, hidden = self .lstm(lstm_input, hidden)
# lstm_output: (batch, 1, dec_hidden)
# 拼接LSTM输出和上下文,生成最终预测
combined = torch.cat([lstm_output.squeeze( 1 ), context], dim = 1 )
output = self .fc(combined) # (batch, vocab_size)
return output, hidden, attention_weights
class Seq2SeqWithAttention ( nn . Module ):
"""完整的带注意力的seq2seq模型"""
def __init__ (self, src_vocab_size, tgt_vocab_size, embed_size,
enc_hidden_size, dec_hidden_size, num_layers = 1 , dropout = 0.3 ):
super (Seq2SeqWithAttention, self ). __init__ ()
self .encoder = Encoder(src_vocab_size, embed_size, enc_hidden_size,
num_layers, dropout)
self .decoder = Decoder(tgt_vocab_size, embed_size, enc_hidden_size,
dec_hidden_size, num_layers, dropout)
def forward (self, src, tgt, teacher_forcing_ratio = 0.5 ):
"""
训练时的前向传播
Args:
src: (batch, src_len)
tgt: (batch, tgt_len)
teacher_forcing_ratio: 使用教师强制的概率
Returns:
outputs: (batch, tgt_len, tgt_vocab_size)
"""
batch_size = src.size( 0 )
tgt_len = tgt.size( 1 )
tgt_vocab_size = self .decoder.fc.out_features
# 存储所有时间步的输出
outputs = torch.zeros(batch_size, tgt_len, tgt_vocab_size, device = src.device)
# 编码
encoder_outputs, hidden = self .encoder(src)
# 初始化解码器隐藏状态
# 双向编码器有2*num_layers个隐藏状态,需要转换为num_layers
# 简单策略:只取前向的最后一层
h_n, c_n = hidden
decoder_hidden = (
h_n[ 0 : 1 ], # 取第一层的隐藏状态
c_n[ 0 : 1 ] # 取第一层的细胞状态
)
# 第一个输入是<start> token
input_token = tgt[:, 0 ]
for t in range ( 1 , tgt_len):
# 解码一步
output, decoder_hidden, attention = self .decoder(
input_token, decoder_hidden, encoder_outputs
)
outputs[:, t] = output
# 教师强制:随机选择使用真实词还是预测词
use_teacher_forcing = torch.rand( 1 ).item() < teacher_forcing_ratio
if use_teacher_forcing:
input_token = tgt[:, t] # 使用真实目标词
else :
input_token = output.argmax( 1 ) # 使用模型预测
return outputs
def translate_sentence (model, src_sentence, src_vocab, tgt_vocab, device, max_len = 50 ):
"""
翻译单个句子
Args:
model: 训练好的seq2seq模型
src_sentence: 源语言句子(字符串)
src_vocab: 源语言词表
tgt_vocab: 目标语言词表
device: 运行设备
max_len: 最大翻译长度
Returns:
translation: 翻译结果(字符串)
attention_weights: 注意力权重矩阵(用于可视化)
"""
model.eval()
# 分词并转为索引
src_tokens = src_sentence.split()
src_indices = [src_vocab.get(w, src_vocab[ '<unk>' ]) for w in src_tokens]
src_tensor = torch.LongTensor(src_indices).unsqueeze( 0 ).to(device)
with torch.no_grad():
# 编码
encoder_outputs, hidden = model.encoder(src_tensor)
# 初始化解码器
h_n, c_n = hidden
decoder_hidden = (h_n[ 0 : 1 ], c_n[ 0 : 1 ])
# 起始token
input_token = torch.LongTensor([tgt_vocab[ '<start>' ]]).to(device)
translation = []
all_attention_weights = []
for _ in range (max_len):
# 解码一步
output, decoder_hidden, attention = model.decoder(
input_token, decoder_hidden, encoder_outputs
)
all_attention_weights.append(attention.cpu().numpy())
# 选择概率最高的词
pred_token = output.argmax( 1 ).item()
pred_word = tgt_vocab.itos[pred_token]
if pred_word == '<end>' :
break
translation.append(pred_word)
input_token = torch.LongTensor([pred_token]).to(device)
return ' ' .join(translation), all_attention_weights
i
比较Bahdanau注意力(加性)和Luong注意力(乘性)的计算复杂度和参数量。在什么情况下选择哪种?
可视化一个训练好的seq2seq模型的注意力权重矩阵。对于语序差异大的语言对(如英日),注意力模式有什么特点?
注意力机制是“软选择”——它对所有位置加权求和。你能想到什么情况下“硬选择”(只选择一个位置)可能更好吗?硬选择的挑战是什么?
实现束搜索解码,对比贪婪解码和束搜索(beam_size=5)在翻译质量和速度上的差异。