梯度消失问题与RNN变种 - LSTM与GRU | 自在学
梯度消失问题与RNN变种
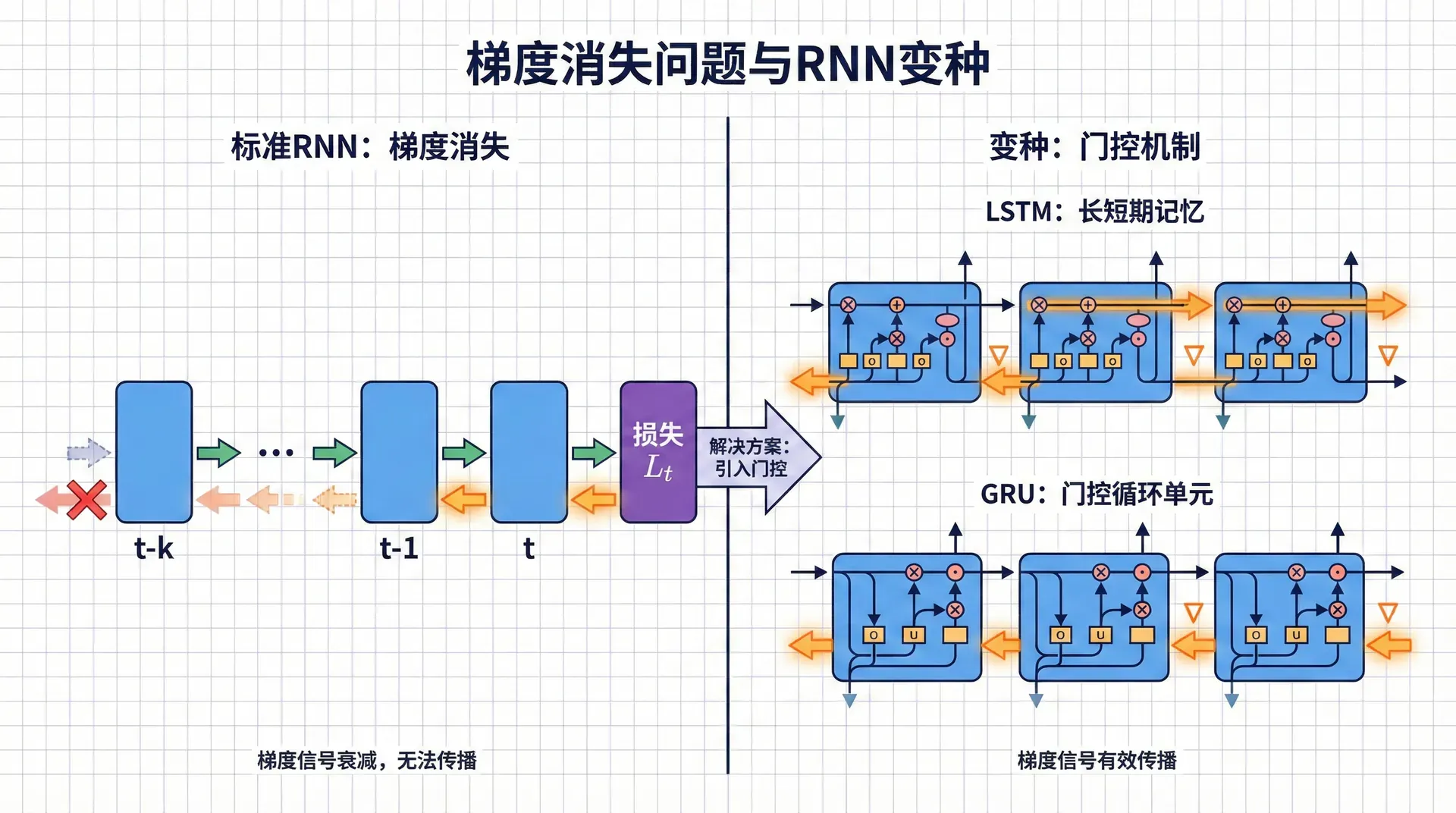
在上一节中,我们学习了循环神经网络如何通过隐藏状态记忆历史信息。RNN的设计优雅简洁,理论上可以捕获任意长的依赖关系。然而,当我们真正训练RNN时,会发现一个令人沮丧的现象:模型很难学习超过20-30步的长距离依赖 。
这不是实现问题,也不是调参问题,而是vanilla RNN架构的根本缺陷——梯度消失(Vanishing Gradient) 。这个问题如此严重,以至于在1990年代末到2000年代初,许多研究者认为训练深度网络和长序列网络是不可能的。
直到1997年,Hochreiter和Schmidhuber发表了LSTM论文,为梯度消失问题提供了一个精巧的解决方案。
本节课我们将深入剖析梯度消失问题的数学本质,理解LSTM如何通过门控机制创造“梯度高速公路”,以及GRU如何在保持效果的同时简化LSTM的设计。这些内容是理解现代NLP的关键——即使在Transformer时代,LSTM的设计思想仍然影响着新架构的开发。
梯度消失的数学剖析
连乘的噩梦
让我们从数学上严格理解为什么RNN会遭遇梯度消失。回忆RNN的核心公式:
h ⃗ t = tanh ( W h h h ⃗ t − 1 + W h x x ⃗ t + b ⃗ h ) \vec{h}_t = \tanh(W_{hh} \vec{h}_{t-1} + W_{hx} \vec{x}_t + \vec{b}_h) h t = tanh ( W hh h t − 1 + W h x x t + b h ) 在时间反向传播中,第1个时刻隐藏状态的梯度需要从第T T T
∂ L ∂ h ⃗ 1 = ∂ L ∂ h ⃗ T ∏ t = 1 T − 1 ∂ h ⃗ t + 1 ∂ h ⃗ t \frac{\partial \mathcal{L}}{\partial \vec{h}_1} = \frac{\partial \mathcal{L}}{\partial \vec{h}_T} \prod_{t=1}^{T-1} \frac{\partial \vec{h}_{t+1}}{\partial \vec{h}_t} ∂ h 这个连乘是问题的根源。每一项∂ h ⃗ t + 1 ∂ h ⃗ t \frac{\partial \vec{h}_{t+1}}{\partial \vec{h}_t} ∂ h t ∂
∂ h ⃗ t + 1 ∂ h ⃗ t = diag ( tanh ′ ( z ⃗ t ) ) ⋅ W h h \frac{\partial \vec{h}_{t+1}}{\partial \vec{h}_t} = \text{diag}(\tanh'(\vec{z}_t)) \cdot W_{hh} ∂ h t 其中z ⃗ t = W h h h ⃗ t + W h x x ⃗ t + 1 \vec{z}_t = W_{hh}\vec{h}_t + W_{hx}\vec{x}_{t+1} z t = W
现在关键来了。tanh \tanh tanh ( 0 , 1 ] (0, 1] ( 0 , 1 ] tanh ( x ) = 0 \tanh(x)=0 tanh ( x ) = 0
∥ diag ( tanh ′ ( z ⃗ t ) ) ∥ ≤ 1 \|\text{diag}(\tanh'(\vec{z}_t))\| \leq 1 ∥ diag ( tanh ′ ( z t )) ∥ ≤ 因此,雅可比矩阵的范数大约是:
∥ ∂ h ⃗ t + 1 ∂ h ⃗ t ∥ ≈ ∥ tanh ′ ( z ⃗ t ) ∥ ⋅ ∥ W h h ∥ \left\|\frac{\partial \vec{h}_{t+1}}{\partial \vec{h}_t}\right\| \approx \|\tanh'(\vec{z}_t)\| \cdot \|W_{hh}\| ∂ h 现在我们面临一个两难境地:
如果∥ W h h ∥ < 1 \|W_{hh}\| < 1 ∥ W hh ∥ < 1 ,那么∥ ∂ h ⃗ t + 1 ∂ h ⃗ t ∥ < 1 \left\|\frac{\partial \vec{h}_{t+1}}{\partial \vec{h}_t}\right\| < 1
∥ ∂ L ∂ h ⃗ 1 ∥ ≤ ∥ ∂ L ∂ h ⃗ T ∥ ⋅ ( ∥ W h h ∥ ) T − 1 \left\|\frac{\partial \mathcal{L}}{\partial \vec{h}_1}\right\| \leq \left\|\frac{\partial \mathcal{L}}{\partial \vec{h}_T}\right\| \cdot \left(\|W_{hh}\|\right)^{T-1} ∂ h 假设∥ W h h ∥ = 0.9 \|W_{hh}\|=0.9 ∥ W hh ∥ = 0.9 0.9 50 ≈ 0.005 0.9^{50} \approx 0.005 0. 9 50 ≈ 0.005
如果∥ W h h ∥ > 1 \|W_{hh}\| > 1 ∥ W hh ∥ > 1 ,梯度会以指数速度增长,导致梯度爆炸。参数更新会变得巨大,数值溢出为NaN,训练彻底崩溃。
即使∥ W h h ∥ = 1 \|W_{hh}\| = 1 ∥ W hh ∥ = 1 ,由于tanh ′ \tanh' tanh ′
这是一个深刻的困境,源于RNN的乘法更新机制。每次状态转移都通过矩阵乘法W h h W_{hh} W hh W h h W_{hh} W hh
遗忘曲线
梯度消失的实际后果是:RNN的有效记忆长度有限 。Karpathy等人[2015]的实验表明,vanilla RNN很难学习超过10-20步的依赖。即使在100词的序列上训练,模型主要利用的仍是最近的10个词左右,退化为类似10-gram的行为。
想象你要模型学习这个模式:“我出生在法国...(中间50个词)...所以我会说流利的___”,正确答案是“法语”。这需要模型记住50步前的“法国”。但由于梯度消失,“法国”对最终损失的梯度贡献几乎为0,模型无法学会这个关联。
在机器翻译中,这个问题更加严重。源语言句子的主语可能影响目标语言句子末尾的动词形式(如性数一致),但RNN难以建模这种跨句子的长距离依赖。
LSTM
1997年,德国学者Sepp Hochreiter和Jürgen Schmidhuber在Neural Computation期刊上发表了题为“Long Short-Term Memory”的论文。
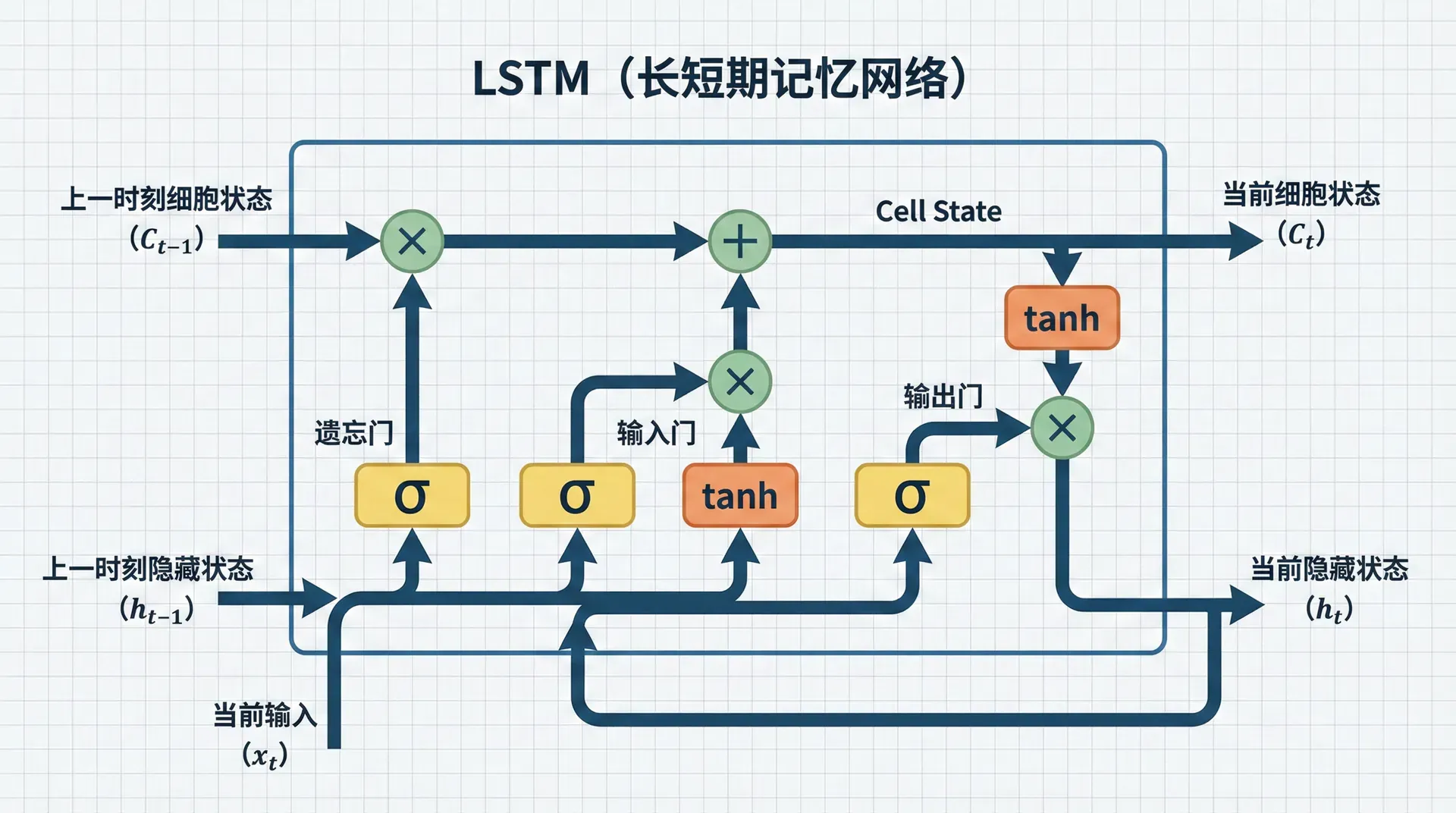
这篇论文提出了一个精巧的架构——LSTM,通过引入门控机制(Gating)和 细胞状态(Cell State) ,从根本上缓解了梯度消失问题。
核心设计哲学
LSTM的设计基于一个深刻的洞察:用加法代替乘法 。
vanilla RNN的状态转移是:
h ⃗ t = f ( W h h h ⃗ t − 1 + … ) \vec{h}_t = f(W_{hh} \vec{h}_{t-1} + \ldots) h t = f ( W 这是乘法关系(W h h W_{hh} W hh h ⃗ t − 1 \vec{h}_{t-1} h t − 1
c ⃗ t = f ⃗ t ⊙ c ⃗ t − 1 + i ⃗ t ⊙ c ⃗ ~ t \vec{c}_t = \vec{f}_t \odot \vec{c}_{t-1} + \vec{i}_t \odot \tilde{\vec{c}}_t c t = f 这是加法关系!c ⃗ t − 1 \vec{c}_{t-1} c t − 1 ⊙ \odot ⊙ c ⃗ t \vec{c}_t
∂ c ⃗ t ∂ c ⃗ t − 1 = f ⃗ t \frac{\partial \vec{c}_t}{\partial \vec{c}_{t-1}} = \vec{f}_t ∂ c t − 1 这只是一个逐元素乘法,不涉及权重矩阵的连乘。如果遗忘门f ⃗ t \vec{f}_t f t
四个门的设计哲学
LSTM通过四个组件精确控制信息流:
遗忘门(Forget Gate) :
f ⃗ t = σ ( W f [ h ⃗ t − 1 ; x ⃗ t ] + b ⃗ f ) \vec{f}_t = \sigma(W_f [\vec{h}_{t-1}; \vec{x}_t] + \vec{b}_f) f t = σ ( 遗忘门决定从细胞状态中丢弃多少旧信息。σ \sigma σ [ 0 , 1 ] [0,1] [ 0 , 1 ]
为什么需要遗忘门?因为并非所有信息都应该无限期保留。在处理句子"我出生在法国,但长大在中国,现在我会说流利的___"时,"法国"在前半句是重要的,但当句子转向"中国"时,可能需要部分忘记"法国",给"中国"腾出记忆空间。遗忘门让模型学会选择性遗忘。
输入门(Input Gate) :
i ⃗ t = σ ( W i [ h ⃗ t − 1 ; x ⃗ t ] + b ⃗ i ) \vec{i}_t = \sigma(W_i [\vec{h}_{t-1}; \vec{x}_t] + \vec{b}_i) i t = σ ( W 输入门决定有多少新信息应该被加入细胞状态。它与候选值c ⃗ ~ t \tilde{\vec{c}}_t c ~ t
c ⃗ ~ t = tanh ( W c [ h ⃗ t − 1 ; x ⃗ t ] + b ⃗ c ) \tilde{\vec{c}}_t = \tanh(W_c [\vec{h}_{t-1}; \vec{x}_t] + \vec{b}_c) c ~ t = c ⃗ ~ t \tilde{\vec{c}}_t c ~ t i ⃗ t \vec{i}_t i
为什么不直接添加c ⃗ ~ t \tilde{\vec{c}}_t c ~ t
细胞状态更新 :
c ⃗ t = f ⃗ t ⊙ c ⃗ t − 1 + i ⃗ t ⊙ c ⃗ ~ t \vec{c}_t = \vec{f}_t \odot \vec{c}_{t-1} + \vec{i}_t \odot \tilde{\vec{c}}_t c t = f 这是LSTM的心脏。它说:新的细胞状态 = 旧状态的保留部分 + 新信息的采纳部分。这种加性更新是梯度能够长距离流动的关键。
输出门(Output Gate) :
o ⃗ t = σ ( W o [ h ⃗ t − 1 ; x ⃗ t ] + b ⃗ o ) \vec{o}_t = \sigma(W_o [\vec{h}_{t-1}; \vec{x}_t] + \vec{b}_o) o t = σ ( W h ⃗ t = o ⃗ t ⊙ tanh ( c ⃗ t ) \vec{h}_t = \vec{o}_t \odot \tanh(\vec{c}_t) h t = o 细胞状态c ⃗ t \vec{c}_t c t h ⃗ t \vec{h}_t h
为什么需要这个额外的控制?因为细胞状态可能包含许多长期信息,但当前时刻可能只需要其中一部分。例如,在处理长文章时,细胞状态可能编码了前面几段的主题、人物等信息,但当前句子的预测可能只需要最近的上下文。输出门让模型灵活地决定"读取"多少长期记忆。
信息流的直观理解
理解LSTM的最好方式是追踪信息如何流动。想象细胞状态c ⃗ t \vec{c}_t c t
c₀ ----[遗忘门]----[+输入门]----> c₁ ----[遗忘门]----[+输入门]----> c₂ ... ↑ ↑ 删除部分信息 删除部分信息 ↓ ↓ 添加新信息 添加新信息 这条传送带是"受保护的"——信息主要通过加法传递,梯度可以几乎不受阻碍地回流。门控操作只是逐元素乘法,不涉及权重矩阵的连乘。
隐藏状态h ⃗ t \vec{h}_t h t
一个具体的例子
让我们用一个例子具体感受LSTM如何工作。考虑句子:“Barack Obama was born in Hawaii. He became the president.”
处理“Barack Obama”时 :
输入门打开(i t ≈ 1 i_t \approx 1 i t ≈ 1
候选状态c ~ t \tilde{c}_t c ~ t
细胞状态c t c_t c
处理“was born in Hawaii”时 :
遗忘门部分关闭(f t ≈ 0.7 f_t \approx 0.7 f t ≈ 0.7
输入门打开:添加“出生地是Hawaii”的信息
细胞状态同时包含人物和出生地信息
处理句号时 :
遗忘门可能部分关闭:句子结束,一些细节可能不再重要
但关键信息“Barack Obama”仍保留在细胞状态中
处理“He”时 :
输出门打开:需要从细胞状态中提取“Barack Obama”的信息来理解“He”
隐藏状态h t h_t h t
输入门决定是否更新细胞状态(代词通常不添加新信息)
通过这个过程,LSTM能够将“Barack Obama”的信息保持在细胞状态中,跨越多个词传递到“He”,帮助模型理解指代关系。
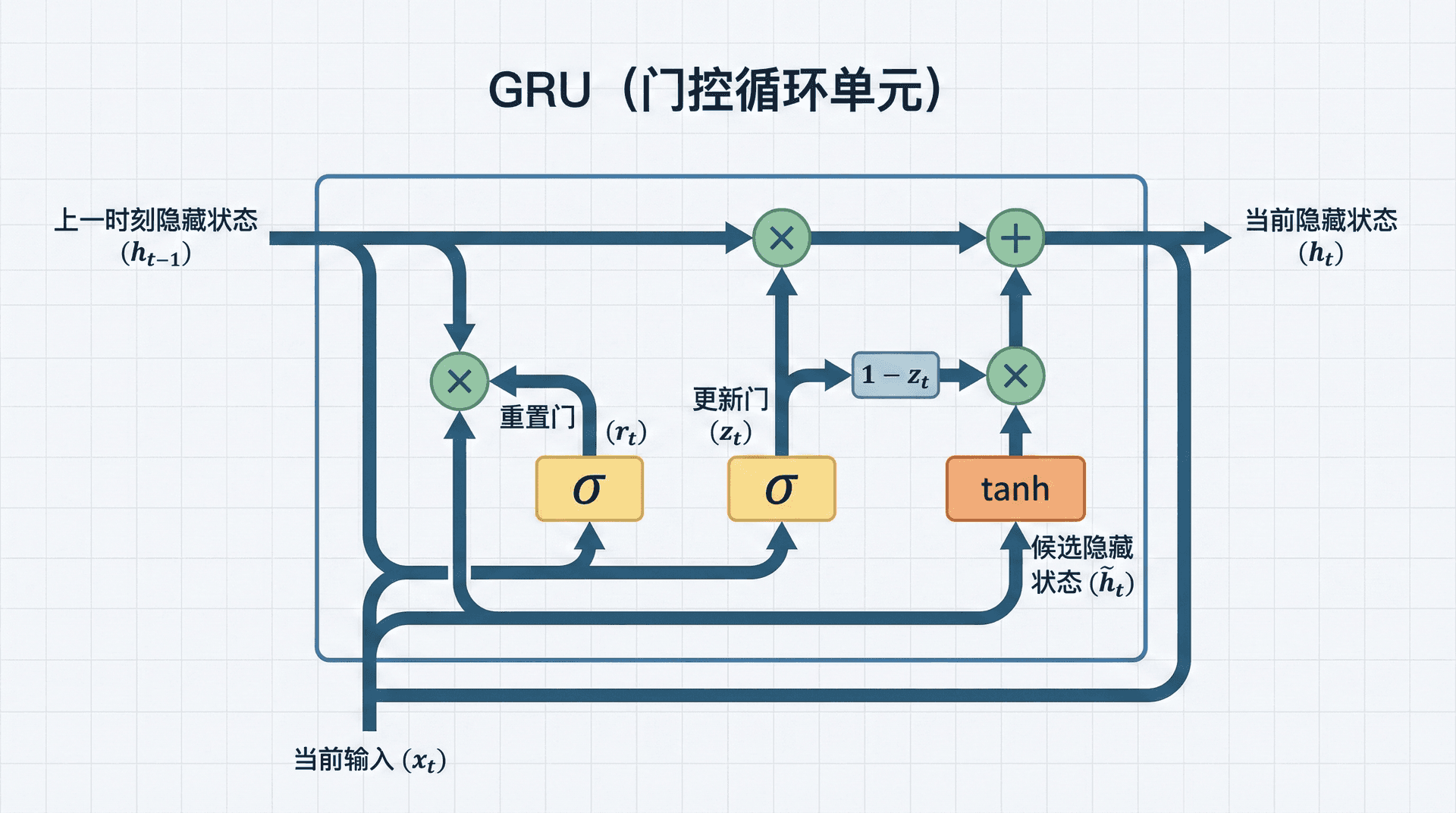
GRU
LSTM虽然强大,但它有四个门和两个状态(h ⃗ t \vec{h}_t h t c ⃗ t \vec{c}_t c
GRU的简化哲学
GRU的核心简化是:合并细胞状态和隐藏状态 。LSTM维护两个状态向量,GRU只用一个h ⃗ t \vec{h}_t h t
更新门(Update Gate) :
z ⃗ t = σ ( W z [ h ⃗ t − 1 ; x ⃗ t ] ) \vec{z}_t = \sigma(W_z [\vec{h}_{t-1}; \vec{x}_t]) z t = σ ( W 更新门同时扮演了LSTM中遗忘门和输入门的角色。它决定保留多少旧状态(类似遗忘门)和接受多少新状态(类似输入门)。妙处在于:这两个操作是互补的——保留多少旧的,就相应地少接受多少新的。
重置门(Reset Gate) :
r ⃗ t = σ ( W r [ h ⃗ t − 1 ; x ⃗ t ] ) \vec{r}_t = \sigma(W_r [\vec{h}_{t-1}; \vec{x}_t]) r t = σ ( W 重置门控制在计算新状态时,应该使用多少之前的隐藏状态信息。如果重置门接近0,模型会"忘记"之前的状态,只基于当前输入计算新状态。
候选隐藏状态 :
h ⃗ ~ t = tanh ( W [ r ⃗ t ⊙ h ⃗ t − 1 ; x ⃗ t ] ) \tilde{\vec{h}}_t = \tanh(W[\vec{r}_t \odot \vec{h}_{t-1}; \vec{x}_t]) h ~ t = 注意这里使用了重置门——r ⃗ t ⊙ h ⃗ t − 1 \vec{r}_t \odot \vec{h}_{t-1} r t ⊙ h
最终更新 :
h ⃗ t = z ⃗ t ⊙ h ⃗ t − 1 + ( 1 − z ⃗ t ) ⊙ h ⃗ ~ t \vec{h}_t = \vec{z}_t \odot \vec{h}_{t-1} + (1 - \vec{z}_t) \odot \tilde{\vec{h}}_t h t = 这个公式非常优雅:z ⃗ t \vec{z}_t z t z ⃗ t = 1 \vec{z}_t=1 z
GRU vs LSTM:设计权衡
GRU和LSTM代表了两种不同的设计哲学:
LSTM的哲学 是"明确分工":
细胞状态负责长期记忆,隐藏状态负责短期信息
遗忘、输入、输出各有专门的门
每个组件职责清晰
GRU的哲学 是"简约优雅":
单一状态兼顾长短期记忆
更新门一个顶两个
参数更少,训练更快
实践中,两者性能非常接近。在大规模数据集上,LSTM通常略好(可能因为更多参数带来更强表达力)。在小数据集上,GRU可能更好(参数少,不容易过拟合)。训练速度上,GRU通常快20-30%。
因此,经验法则是:先尝试GRU,如果数据充足且需要极致性能,再试LSTM 。在许多任务上,性能差异小于1%,不值得为此承担LSTM的额外计算成本。
PyTorch实现:手工打造LSTM单元
虽然PyTorch提供了高效的nn.LSTM实现,手动实现一次LSTM单元对深入理解其工作原理非常有帮助:
import torch import torch.nn as nn
class LSTMCell ( nn . Module ): """手工实现的LSTM单元(用于教学)""" def __init__ (self, input_size, hidden_size): """ Args: input_size: 输入维度 hidden_size: 隐藏状态和细胞状态的维度 """ super (LSTMCell, self ). __init__ () self .input_size = input_size self LSTM的成功与局限
性能革命
LSTM的引入彻底改变了序列建模的格局。在2015年前后,LSTM几乎在所有序列任务上都达到了当时的最佳性能:
语言建模 :在Penn Treebank上,LSTM将困惑度从vanilla RNN的120降低到80,这是质的飞跃。机器翻译 :2014年Sutskever等人用LSTM构建的seq2seq模型在WMT英法翻译上接近统计机器翻译系统,首次证明了端到端神经翻译的可行性。语音识别 :Google在2015年将其语音识别系统切换到LSTM,错误率下降了30-40%。情感分析 、命名实体识别 、词性标注 等任务上,LSTM也都成为标准选择。
梯度消失真的解决了吗?
LSTM显著缓解了梯度消失,但没有完全解决。实验表明,LSTM的有效记忆长度大约在100-200步,远超vanilla RNN的10-20步,但仍不是无限的。
在极长的序列(如整篇文章、长对话)上,LSTM仍会遗忘早期信息。而且,即使梯度能够回流,学习长距离依赖仍然困难,因为优化本身就是一个挑战——损失地形(loss landscape)可能非常复杂。
计算成本
LSTM的代价是计算成本。相比vanilla RNN,LSTM需要计算四个门,参数量是4倍,计算量也大约是4倍。在大规模应用中(如Google的生产系统),这个开销是显著的。
GRU通过简化设计,将计算量减少到约LSTM的75%,在很多任务上达到相似性能,这解释了为什么GRU在工业界很受欢迎。
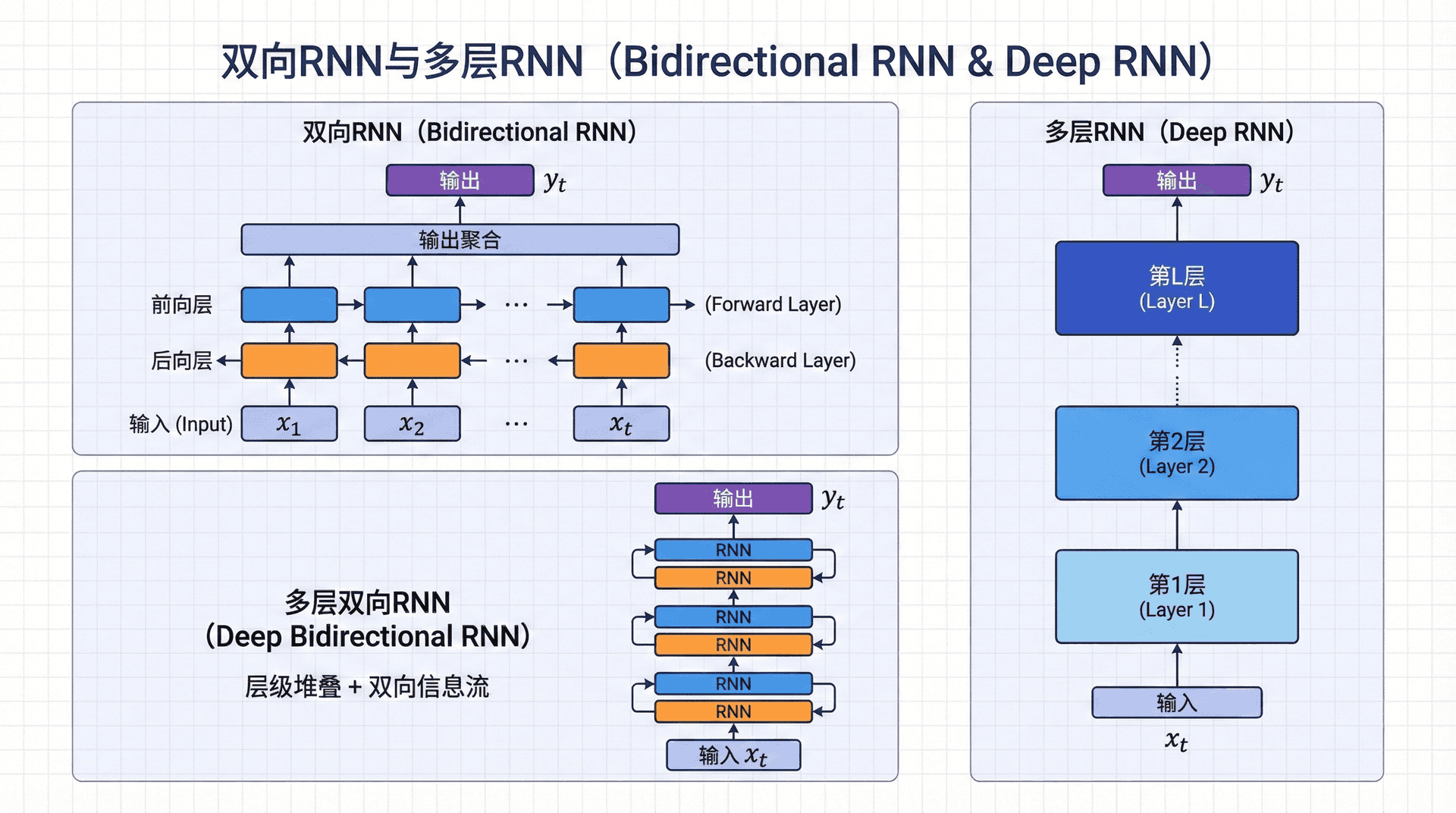
双向RNN与多层RNN
双向RNN:同时看过去和未来
在许多NLP任务中,我们可以同时利用左右两个方向的上下文。例如,在词性标注中,判断“bank”是名词还是动词,既要看它前面的词(“the bank”暗示名词),也要看后面的词(“bank on it”暗示动词)。
双向RNN(Bidirectional RNN) 同时运行两个独立的RNN:
前向RNN从左到右处理序列:h → ⃗ 1 , h → ⃗ 2 , … \vec{\overrightarrow{h}}_1, \vec{\overrightarrow{h}}_2, \ldots h
在每个位置t t t
h ⃗ t = [ h → ⃗ t ; h ← ⃗ t ] \vec{h}_t = [\vec{\overrightarrow{h}}_t; \vec{\overleftarrow{h}}_t] h t = [ 这样,h ⃗ t \vec{h}_t h t w 1 , … , w t w_1, \ldots, w_t w 1 ,
双向RNN在许多任务上效果显著提升,但有一个关键限制:不能用于语言模型或文本生成 。因为在这些任务中,我们在预测第t t t t + 1 t+1 t + 1
双向LSTM(BiLSTM)和双向GRU(BiGRU)是序列标注任务(如命名实体识别、词性标注)的标准选择。ELMo模型(我们在第13讲学习的)就是用双向LSTM作为核心组件。
多层RNN:层次化表示
就像在计算机视觉中堆叠多层卷积,我们也可以堆叠多层RNN:
输入 x₁ x₂ x₃ ... ↓ ↓ ↓ 层1: h₁¹ h₂¹ h₃¹ ... ↓ ↓ ↓ 层2: h₁² h₂² h₃² ... ↓ ↓ ↓ 输出 y₁ y₂ y₃ ... 第l l l l + 1 l+1 l + 1
第1层可能捕获局部模式(如常见的词组)
第2层可能捕获更抽象的句法结构
第3层可能捕获语义和主题信息
实验表明,2-4层的LSTM通常效果最好。更深的网络(如8层)可能带来小幅提升,但也增加了过拟合风险和计算成本。而且,深层RNN需要仔细的初始化和正则化(如层之间的dropout)。
在Transformer出现后,堆叠深度网络变得更容易(因为有残差连接),但在LSTM时代,超过4层的RNN是比较罕见的。
实践技巧
梯度裁剪:必不可少的防护
即使LSTM缓解了梯度消失,梯度爆炸仍可能发生。在训练LSTM时,梯度裁剪是必须的 :
# 训练循环中 loss.backward() torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm = 5.0 ) optimizer.step() max_norm=5.0是一个经验值,在大多数任务上表现良好。如果训练中看到loss突然变成NaN,通常是梯度爆炸,需要调小这个值。
遗忘门偏置初始化
一个重要但常被忽视的技巧:将LSTM遗忘门的偏置初始化为1 (而不是通常的0)。
为什么?回忆遗忘门的公式:
f t = σ ( W f [ h t − 1 ; x t ] + b f ) f_t = \sigma(W_f [h_{t-1}; x_t] + b_f) f t = σ ( W f [ h t − 1 ; 如果b f = 0 b_f=0 b f = 0 f t ≈ σ ( 0 ) = 0.5 f_t \approx \sigma(0) = 0.5 f t ≈ σ ( 0 ) = 0.5
如果b f = 1 b_f=1 b f = 1 f t ≈ σ ( 1 ) ≈ 0.73 f_t \approx \sigma(1) \approx 0.73 f t ≈ σ ( 1 ) ≈ 0.73
这个简单的技巧在许多任务上能提升训练速度和最终性能:
# 初始化LSTM遗忘门偏置 for name, param in lstm.named_parameters(): if 'bias' in name: n = param.size( 0 ) # LSTM的bias顺序是: input_gate, forget_gate, cell_gate, output_gate # 将forget_gate的bias设为1 param.data[n // 4 :n // 2 ].fill_( 1.0 ) 层间Dropout的正确使用
Dropout在LSTM中需要小心使用。PyTorch的nn.LSTM提供了dropout参数,但它只在层与层之间 应用dropout,不在同一层的时间步之间:
lstm = nn.LSTM(input_size, hidden_size, num_layers = 3 , dropout = 0.5 ) 这个dropout=0.5会在第1层输出到第2层输入之间,以及第2层到第3层之间应用dropout。但在第1层的h 1 → h 2 → h 3 h_1 \to h_2 \to h_3 h 1 → h 2 → h 3
为什么?因为时间步之间的dropout会破坏RNN的记忆能力。如果我们在h t h_t h t h t + 1 h_{t+1} h t + 1
正确的做法是:
在输入嵌入上应用dropout
在层与层之间应用dropout
在最终输出上应用dropout
不要 在时间维度上应用dropout
练习与思考
详细推导LSTM中细胞状态c ⃗ t \vec{c}_t c t c ⃗ t − 1 \vec{c}_{t-1} c
1
∂ L
=
=
W hh
hh
+
diag ( tanh ′ ( z ⃗ t ) ) \text{diag}(\tanh'(\vec{z}_t)) diag ( tanh ′ ( z t ))
1
t
≈
∥ W hh ∥
<
1
1
∂ L
≤
( ∥ W hh ∥ ) T − 1
hh
+
… )
t
⊙
t
∂
=
W
f
[
;
]
+
i
[
;
]
+
t
i ⃗ t ⊙ c ⃗ ~ t \vec{i}_t \odot \tilde{\vec{c}}_t i t ⊙ c ~ t
t
⊙
o
[
;
]
+
t
⊙
t
tanh ( c ⃗ t ) \tanh(\vec{c}_t) tanh ( c t ) t
t
门控循环单元(Gated Recurrent Unit, GRU)
z
[
;
])
r
[
;
])
t − 1
z
t
⊙
( 1 −
t
=
1
.hidden_size
=
hidden_size
# LSTM有四组权重:遗忘门、输入门、候选值、输出门
# 为了效率,我们将它们合并成一个大矩阵
self .W = nn.Linear(input_size + hidden_size, 4 * hidden_size)
def forward (self, x, hidden):
"""
单步前向传播
Args:
x: (batch, input_size) 当前时刻的输入
hidden: (h_prev, c_prev)
h_prev: (batch, hidden_size) 前一时刻的隐藏状态
c_prev: (batch, hidden_size) 前一时刻的细胞状态
Returns:
h_new: (batch, hidden_size) 新的隐藏状态
c_new: (batch, hidden_size) 新的细胞状态
"""
h_prev, c_prev = hidden
# 拼接输入和前一隐藏状态
combined = torch.cat([x, h_prev], dim = 1 )
# combined: (batch, input_size + hidden_size)
# 一次性计算四个门
gates = self .W(combined) # (batch, 4 * hidden_size)
# 分割成四个部分
i_gate, f_gate, g_gate, o_gate = gates.chunk( 4 , dim = 1 )
# 应用激活函数
i = torch.sigmoid(i_gate) # 输入门:[0,1]
f = torch.sigmoid(f_gate) # 遗忘门:[0,1]
g = torch.tanh(g_gate) # 候选值:[-1,1]
o = torch.sigmoid(o_gate) # 输出门:[0,1]
# 更新细胞状态(核心!)
c_new = f * c_prev + i * g
# 计算新的隐藏状态
h_new = o * torch.tanh(c_new)
return h_new, c_new
class LSTMLanguageModel ( nn . Module ):
"""使用PyTorch内置LSTM的语言模型"""
def __init__ (self, vocab_size, embed_size = 256 , hidden_size = 512 , num_layers = 2 , dropout = 0.5 ):
super (LSTMLanguageModel, self ). __init__ ()
self .hidden_size = hidden_size
self .num_layers = num_layers
# 词嵌入
self .embedding = nn.Embedding(vocab_size, embed_size)
# LSTM层
self .lstm = nn.LSTM(
input_size = embed_size,
hidden_size = hidden_size,
num_layers = num_layers,
batch_first = True ,
dropout = dropout if num_layers > 1 else 0
)
# 输出投影
self .fc = nn.Linear(hidden_size, vocab_size)
self .dropout = nn.Dropout(dropout)
def forward (self, x, hidden = None ):
"""
Args:
x: (batch, seq_len) 输入词ID
hidden: ((num_layers, batch, hidden), (num_layers, batch, hidden))
LSTM需要两个状态:h和c
Returns:
output: (batch, seq_len, vocab_size)
hidden: ((num_layers, batch, hidden), (num_layers, batch, hidden))
"""
# 词嵌入
embeds = self .embedding(x)
embeds = self .dropout(embeds)
# 通过LSTM
lstm_out, hidden = self .lstm(embeds, hidden)
lstm_out = self .dropout(lstm_out)
# 输出层
output = self .fc(lstm_out)
return output, hidden
def init_hidden (self, batch_size, device = 'cpu' ):
"""初始化LSTM的双状态"""
h0 = torch.zeros( self .num_layers, batch_size, self .hidden_size, device = device)
c0 = torch.zeros( self .num_layers, batch_size, self .hidden_size, device = device)
return (h0, c0)
class GRULanguageModel ( nn . Module ):
"""GRU语言模型"""
def __init__ (self, vocab_size, embed_size = 256 , hidden_size = 512 , num_layers = 2 , dropout = 0.5 ):
super (GRULanguageModel, self ). __init__ ()
self .hidden_size = hidden_size
self .num_layers = num_layers
self .embedding = nn.Embedding(vocab_size, embed_size)
self .gru = nn.GRU(
input_size = embed_size,
hidden_size = hidden_size,
num_layers = num_layers,
batch_first = True ,
dropout = dropout if num_layers > 1 else 0
)
self .fc = nn.Linear(hidden_size, vocab_size)
self .dropout = nn.Dropout(dropout)
def forward (self, x, hidden = None ):
embeds = self .embedding(x)
embeds = self .dropout(embeds)
gru_out, hidden = self .gru(embeds, hidden)
gru_out = self .dropout(gru_out)
output = self .fc(gru_out)
return output, hidden
def init_hidden (self, batch_size, device = 'cpu' ):
"""GRU只需要一个隐藏状态"""
return torch.zeros( self .num_layers, batch_size, self .hidden_size, device = device)
1
,
,
…
后向RNN从右到左处理序列:h ← ⃗ T , h ← ⃗ T − 1 , … \vec{\overleftarrow{h}}_T, \vec{\overleftarrow{h}}_{T-1}, \ldots h T , h T − 1 , …
h
t
;
]
…
,
w t
w t , … , w T w_t, \ldots, w_T w t , … , w T x t
]
+
b f )
t − 1
用一个具体的例子(自己构造或来自真实文本)说明LSTM的四个门如何协同工作,处理长距离依赖。
比较vanilla RNN、LSTM和GRU的参数数量。假设输入维度为d x d_x d x d h d_h d h
设计一个实验来验证LSTM确实能学习vanilla RNN学不会的长距离依赖。提示:可以构造人工数据集,要求模型记住序列开头的信息。
在实际项目中,你会选择LSTM还是GRU?在什么情况下选择哪个?考虑数据量、计算资源、任务类型等因素。
LSTM通过加性更新缓解了梯度消失,但为什么仍然无法记住无限长的依赖?是梯度的问题,优化的问题,还是表达能力的问题?
t + 1