循环神经网络与语言模型 - 序列建模基础 | 自在学
循环神经网络与语言模型
在我们学习了词向量如何表示单个词的含义后,下一个自然的问题是:如何理解和生成完整的句子?句子不是词的简单堆砌,而是一个有序的序列,词与词之间有复杂的依赖关系。“狗咬人”和“人咬狗”使用相同的词,但含义完全不同。这种顺序性 是语言的核心特征之一。
更关键的是,自然语言中充满了长距离依赖 。考虑这个句子:“The keys to the cabinet are on the table.” 主语“keys”和谓语“are”之间隔了6个词,但它们在语法上必须保持数的一致。在机器翻译中,这种长距离依赖更加普遍——源语言中相邻的两个词,在目标语言中可能相距甚远。
传统的前馈神经网络无法有效处理这类序列数据。它们的致命局限是固定的输入维度 ——你必须预先决定输入多少个词。如果规定输入5个词,那么4个词的句子需要填充,6个词的句子需要截断。
更糟糕的是,即使勉强处理了变长序列,前馈网络也无法在不同位置之间共享知识——它会把第1个位置的“cat”和第5个位置的“cat”视为完全不同的输入。
这节课我们将介绍循环神经网络(RNN) ,这是第一个真正为序列建模而设计的神经网络架构。RNN通过引入循环连接,优雅地解决了变长序列、参数共享和时序记忆的问题。
语言模型
语言模型(Language Model) 的任务是为一个词序列分配概率。给定句子“我爱自然语言处理”,语言模型需要告诉我们这个句子出现的概率P ( 我,爱,自然语言处理 ) P(\text{我,爱,自然语言处理}) P ( 我 , 爱 , 自然语言处理 )
这听起来很抽象,但语言模型无处不在。当你在手机上打字时,输入法根据你已经输入的词预测下一个词——这就是语言模型。当语音识别系统在“recognize speech”和“wreck a nice beach”(发音相似)之间选择时,语言模型告诉它前者的概率更高。在机器翻译中,语言模型帮助选择更流畅自然的译文。
形式化地,语言模型计算联合概率:
P ( w 1 , w 2 , … , w n ) = ∏ t = 1 n P ( w t ∣ w 1 , … , w t − 1 ) P(w_1, w_2, \ldots, w_n) = \prod_{t=1}^{n} P(w_t | w_1, \ldots, w_{t-1}) P ( w 1 , w 2 , … , w n ) = t = 1 ∏ n P ( w t ∣ w 1 , … , w t − 1 这个分解利用了概率的链式法则——句子的概率等于每个词在给定前文时的条件概率的乘积。关键在于如何建模这些条件概率P ( w t ∣ w 1 , … , w t − 1 ) P(w_t | w_1, \ldots, w_{t-1}) P ( w t ∣ w 1 , … , w t − 1 )
n-gram模型
在神经网络出现之前,语言模型的主流方法是n-gram模型 。它的核心假设是马尔可夫假设(Markov Assumption) :一个词只依赖于它前面的n − 1 n-1 n − 1
对于三元模型(trigram) ,我们假设:
P ( w t ∣ w 1 , … , w t − 1 ) ≈ P ( w t ∣ w t − 2 , w t − 1 ) P(w_t | w_1, \ldots, w_{t-1}) \approx P(w_t | w_{t-2}, w_{t-1}) P ( w t ∣ w 1 , … , w 也就是说,预测当前词时,只看前面两个词就够了。这个简化让模型变得可处理——我们只需要在大规模语料库中统计三个词共同出现的频率:
P ( w t ∣ w t − 2 , w t − 1 ) = count ( w t − 2 , w t − 1 , w t ) count ( w t − 2 , w t − 1 ) P(w_t | w_{t-2}, w_{t-1}) = \frac{\text{count}(w_{t-2}, w_{t-1}, w_t)}{\text{count}(w_{t-2}, w_{t-1})} P ( w t ∣ w t − 2 , w n-gram模型在1990-2000年代主导了语言建模。它们简单、快速、可解释。在足够大的语料库上,trigram模型可以达到不错的效果。
n-gram的三大困境
然而,n-gram模型有三个无法克服的根本问题,这些问题最终导致了神经语言模型的兴起。
第一个困境是稀疏性 。假设词表大小是50,000,那么可能的trigram数量是50000 3 = 1.25 × 10 14 50000^3 = 1.25 \times 10^{14} 5000 0 3 = 1.25 × 1 0 14
研究者们开发了各种平滑技术(Smoothing) 来缓解这个问题。加法平滑给每个n-gram加一个小的伪计数;Good-Turing估计重新分配概率质量;Kneser-Ney平滑考虑词的"versatility"(多样性)。但这些都是事后补丁,无法从根本上解决稀疏性问题。
第二个困境是存储开销 。即使我们只存储出现过的n-gram,数量仍然巨大。一个在10亿词语料上训练的trigram模型可能需要存储数亿个三元组及其计数,占用数GB的内存。当n n n
第三个困境,也是最根本的,是固定窗口的局限 。马尔可夫假设说词只依赖于前n − 1 n-1 n − 1
你可能会说,那就用更大的n n n n n n n n n n n n
这些困境促使研究者寻找新的方法。如果我们能用一个连续空间 的模型,而不是离散的计数统计,也许可以缓解稀疏性。如果模型能够在不同位置之间共享参数 ,也许可以泛化到未见过的序列。如果模型的记忆“不受固定窗口限制”,也许可以捕获任意长的依赖。这就是神经语言模型,特别是循环神经网络,要解决的问题。
循环神经网络
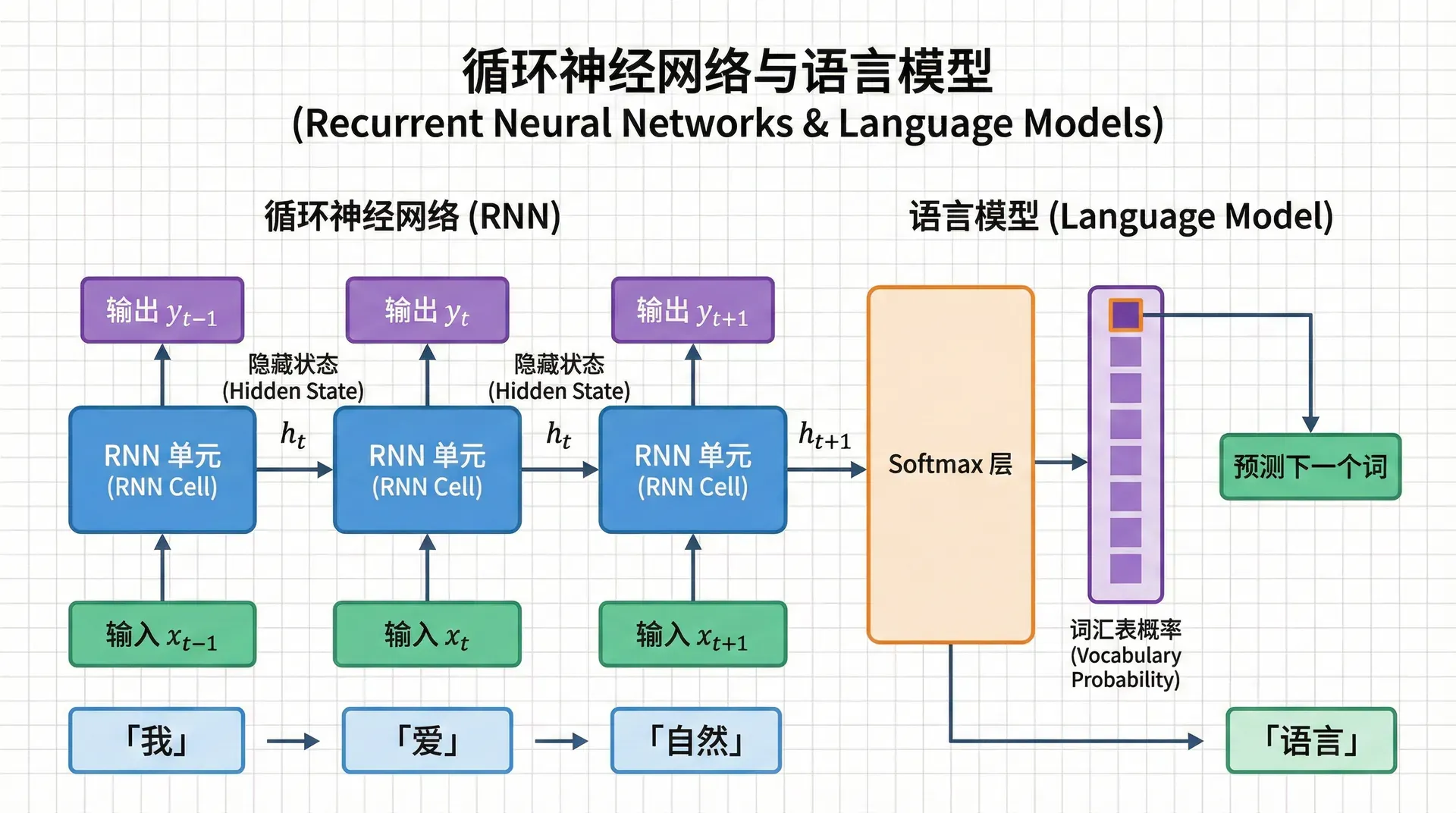
循环神经网络的设计哲学可以用一个简单的想法概括:在处理当前输入时,使用一个隐藏状态来总结之前看到的所有信息 。
想象你在读一本侦探小说。读到第100页时,你不会只记得第99页的内容——你的脑海中有一个关于故事的“状态”:谁是主角、发生了什么事件、有哪些线索、当前的悬念是什么。每读一页,这个状态都会更新,融入新的信息。到第101页时,你基于更新后的状态继续理解故事。
RNN将这个过程数学化。网络维护一个隐藏状态向量 h ⃗ t \vec{h}_t h t t t t
读取当前输入x ⃗ t \vec{x}_t x t
结合上一时刻的隐藏状态h ⃗ t − 1 \vec{h}_{t-1} h
数学上,这个过程表示为:
h ⃗ t = tanh ( W h h h ⃗ t − 1 + W h x x ⃗ t + b ⃗ h ) \vec{h}_t = \tanh(W_{hh} \vec{h}_{t-1} + W_{hx} \vec{x}_t + \vec{b}_h) h t = tanh ( W y ⃗ t = W h y h ⃗ t + b ⃗ y \vec{y}_t = W_{hy} \vec{h}_t + \vec{b}_y y t = W 第一个公式是RNN的核心——它说明了隐藏状态如何从过去"流动"到现在。W h h W_{hh} W hh W h x W_{hx} W h x tanh \tanh tanh
关键观察:所有时间步使用相同的权重矩阵W h h , W h x , W h y W_{hh}, W_{hx}, W_{hy} W hh , W h x , W h y 。这种参数共享是RNN的美妙之处——无论序列多长,参数数量保持不变。这与卷积神经网络的权重共享是类似的思想,但RNN在时间维度上共享。
展开视图:从循环到序列
RNN的"循环"连接一开始可能让人困惑。更清晰的理解方式是将RNN在时间上"展开"。考虑处理句子"我爱NLP":
时刻0: 时刻1: 时刻2: 时刻3: h₀=0 → h₁ → h₂ → h₃ ↑ ↑ ↑ x₁="我" x₂="爱" x₃="NLP" ↓ ↓ ↓ y₁ y₂ y₃ 展开后,RNN看起来像一个深度前馈网络,但有两个特点:
各层之间的权重是共享的(W h h W_{hh} W hh
每一层除了从下层接收输入x ⃗ t \vec{x}_t x t
这个展开视图帮助我们理解反向传播如何工作——梯度将从右向左"回流",类似于在一个很深的网络中传播。
用RNN做语言建模
RNN天然适合语言建模任务。给定一个句子w 1 , w 2 , … , w T w_1, w_2, \ldots, w_T w 1 , w 2 , … , w T
将每个词w t w_t w t x ⃗ t = E w t \vec{x}_t = E w_t x t =
总损失是所有时刻损失的平均:
L = 1 T ∑ t = 1 T L t = − 1 T ∑ t = 1 T log P ( w t + 1 ∣ w 1 , … , w t ) \mathcal{L} = \frac{1}{T} \sum_{t=1}^{T} \mathcal{L}_t = -\frac{1}{T} \sum_{t=1}^{T} \log P(w_{t+1} | w_1, \ldots, w_t) L = T 1 t = 1 ∑ 这个设计有几个优雅的特点:
无限的上下文窗口 。理论上,h ⃗ t \vec{h}_t h t w 1 , … , w t w_1, \ldots, w_t w 1
参数效率 。无论句子多长,RNN的参数只有W h h , W h x , W h y W_{hh}, W_{hx}, W_{hy} W hh , W h x , W h y E E
泛化能力 。由于参数共享和连续表示,RNN可以泛化到训练时未见过的序列。如果模型学会了"我喜欢苹果"的模式,它可能也能处理"我喜欢橙子",即使后者从未在训练数据中出现。
时间反向传播
BPTT算法
RNN如何训练?答案是时间反向传播(Backpropagation Through Time, BPTT) ,这本质上是标准反向传播算法在展开的RNN上的应用。
回忆展开的RNN像一个深度网络。BPTT的过程是:
前向传播 :从左到右,计算所有时刻的隐藏状态和输出:
h ⃗ 1 = tanh ( W h x x ⃗ 1 ) , h ⃗ 2 = tanh ( W h h h ⃗ 1 + W h x x ⃗ 2 ) , … \vec{h}_1 = \tanh(W_{hx} \vec{x}_1), \quad \vec{h}_2 = \tanh(W_{hh} \vec{h}_1 + W_{hx} \vec{x}_2), \quad \ldots h 1 = 反向传播 :从右到左,计算梯度。这里有个微妙之处——h ⃗ t \vec{h}_t h t
当前时刻的输出y ⃗ t \vec{y}_t y t W h y W_{hy} W h y
∂ L ∂ h ⃗ t = ∂ L ∂ y ⃗ t ∂ y ⃗ t ∂ h ⃗ t ⏟ 来自当前输出 + ∂ L ∂ h ⃗ t + 1 ∂ h ⃗ t + 1 ∂ h ⃗ t ⏟ 来自未来状态 \frac{\partial \mathcal{L}}{\partial \vec{h}_t} = \underbrace{\frac{\partial \mathcal{L}}{\partial \vec{y}_t} \frac{\partial \vec{y}_t}{\partial \vec{h}_t}}_{\text{来自当前输出}} + \underbrace{\frac{\partial \mathcal{L}}{\partial \vec{h}_{t+1}} \frac{\partial \vec{h}_{t+1}}{\partial \vec{h}_t}}_{\text{来自未来状态}} ∂ h 这个递归关系意味着梯度需要从最后一个时刻T T T
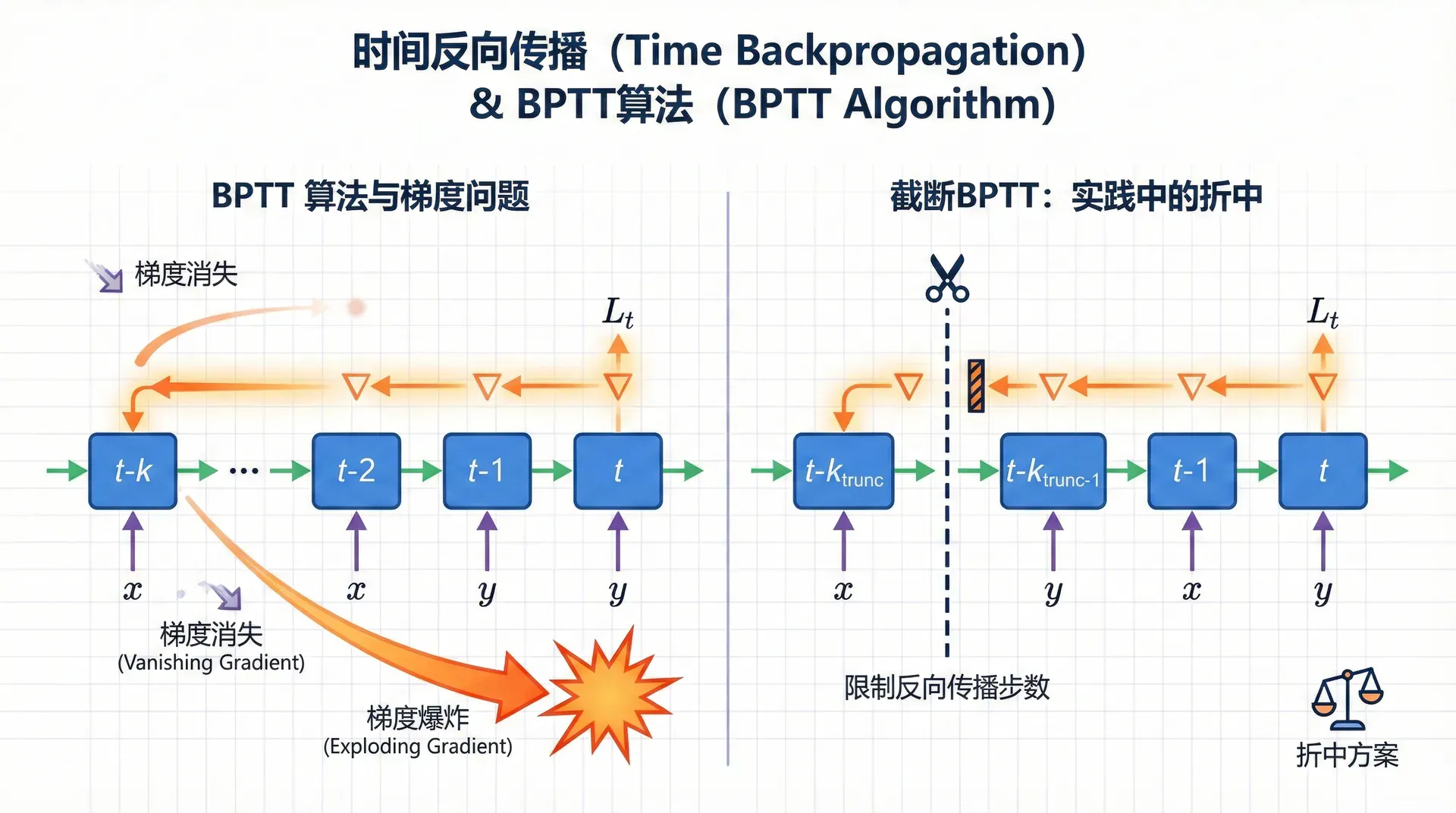
梯度消失与梯度爆炸
考虑h ⃗ 1 \vec{h}_1 h 1
∂ L ∂ h ⃗ 1 = ∂ L ∂ h ⃗ T ∏ t = 1 T − 1 ∂ h ⃗ t + 1 ∂ h ⃗ t \frac{\partial \mathcal{L}}{\partial \vec{h}_1} = \frac{\partial \mathcal{L}}{\partial \vec{h}_T} \prod_{t=1}^{T-1} \frac{\partial \vec{h}_{t+1}}{\partial \vec{h}_t} ∂ h 这是一个连乘!每个∂ h ⃗ t + 1 ∂ h ⃗ t \frac{\partial \vec{h}_{t+1}}{\partial \vec{h}_t} ∂ h t ∂
让我们用一个具体例子理解梯度消失的严重性。假设∂ h ⃗ t + 1 ∂ h ⃗ t \frac{\partial \vec{h}_{t+1}}{\partial \vec{h}_t} ∂ h t ∂
这意味着什么?RNN很难学习长距离依赖 。虽然理论上h ⃗ t \vec{h}_t h t
梯度爆炸 的表现不同但同样致命。梯度可能在几次迭代内变得巨大(数值溢出为NaN),导致参数更新爆炸,模型完全崩溃。幸运的是,梯度爆炸相对容易处理——我们可以用梯度裁剪(Gradient Clipping) :
# 如果梯度范数超过阈值,缩放到阈值 torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm = 5.0 ) 这个简单的技巧将梯度向量的范数限制在一个安全值(如5.0),防止单次更新太大。
但梯度消失没有这么简单的解决办法。这正是vanilla RNN的致命缺陷,也是下一讲我们要学习LSTM的原因——LSTM通过精巧的门控机制,为梯度提供了"高速公路",让信息和梯度可以更长距离地流动。
截断BPTT:实践中的折中
完整的BPTT在长序列上计算和内存开销都很大。实践中,我们常常使用截断BPTT(Truncated BPTT) :只回传k k k k = 20 k=20 k = 20
这是训练效率和模型能力之间的权衡。截断BPTT让模型只能学习k k k
PyTorch实现:从零构建RNN语言模型
理论理解后,让我们用PyTorch实现一个完整的RNN语言模型。这个实现包含了训练和文本生成的完整流程。
import torch import torch.nn as nn import torch.nn.functional as F
class RNNLanguageModel ( nn . Module ): """RNN语言模型:给定前文预测下一个词""" def __init__ (self, vocab_size, embed_size = 256 , hidden_size = 512 , num_layers = 1 ): """ Args: vocab_size: 词表大小 embed_size: 词嵌入维度 hidden_size: RNN隐藏层维度 这个实现展示了RNN语言模型的完整流程。几个关键点:
hidden.detach() :这实现了截断BPTT,切断了当前batch与之前batch之间的梯度流梯度裁剪 :防止梯度爆炸的必要技巧温度采样 :生成时控制随机性,temperature=0.8会让输出更确定,1.2会更随机
评估语言模型:困惑度
如何评判一个语言模型的好坏?我们使用**困惑度(Perplexity)**指标。
困惑度定义为测试集交叉熵损失的指数:
Perplexity = exp ( L test ) = exp ( − 1 T ∑ t = 1 T log P ( w t ∣ w < t ) ) \text{Perplexity} = \exp\left(\mathcal{L}_{\text{test}}\right) = \exp\left(-\frac{1}{T}\sum_{t=1}^{T}\log P(w_t|w_{<t})\right) Perplexity = exp ( L test ) = exp ( − 困惑度可以直观理解为:"模型在每个位置平均需要在多少个词中犹豫"。如果模型总是非常确定下一个词(概率接近1),困惑度会很低。如果模型不确定(概率分散在很多词上),困惑度会很高。
一个随机猜测的模型,给每个词相同的概率1 / V 1/V 1/ V V V V
在Penn Treebank这个标准数据集上,不同模型的困惑度表现:
Trigram : ~120LSTM : ~80Transformer : ~30-40
困惑度的下降反映了模型建模能力的提升。RNN通过利用更长的上下文,显著超越了n-gram模型。
RNN的成功与局限
RNN的突破
循环神经网络在2010年代中期取得了巨大成功。在语言建模、机器翻译、语音识别等任务上,RNN大幅超越了之前的统计方法,展现了神经网络处理序列数据的强大能力。
RNN的核心优势在于:
灵活性 :可以处理任意长度的序列参数效率 :参数量不随序列长度增长端到端学习 :不需要人工特征工程
梯度消失的阴影
但vanilla RNN有一个致命缺陷:梯度消失问题 限制了它学习长距离依赖的能力。虽然理论上RNN可以记住整个历史,实践中它们倾向于只关注最近几个词,在20-30步之外的依赖很难学习。
这个问题在某些任务上特别明显。考虑句子:“The man, who wore a hat that was quite red, was tall.” 要判断动词“was”的数,需要追溯到主语“man”(单数),跳过中间的从句。Vanilla RNN在这类任务上表现不佳。
练习与思考
用自己的话解释为什么RNN可以处理任意长度的序列,而传统前馈神经网络不行。RNN的“记忆”是如何实现的?
推导RNN中权重矩阵W h h W_{hh} W hh
实现一个字符级RNN语言模型,在莎士比亚的戏剧文本上训练。生成一些文本样本,观察模型是否学会了诗歌的韵律和风格。
比较BPTT和标准反向传播的异同。为什么在长序列上需要截断BPTT?截断会带来什么后果?
如果要建模100个词之前的依赖关系,vanilla RNN会遇到什么困难?为什么tanh \tanh tanh [ 0 , 1 ] [0,1] [ 0 , 1 ]
设计一个实验来验证RNN确实难以学习长距离依赖。可以构造人工数据集,要求模型记住序列开头的信息来预测结尾。
在下一讲我们会学习LSTM,它通过门控机制解决了梯度消失问题。根据你对RNN问题的理解,猜测LSTM可能采用什么样的设计?
)
t − 1
)
≈
P ( w t ∣ w t − 2 , w t − 1 )
t − 1
)
=
count ( w t − 2 , w t − 1 ) count ( w t − 2 , w t − 1 , w t )
t − 1
基于h ⃗ t \vec{h}_t h t y ⃗ t \vec{y}_t y t hh
+
h y
+
E w t
按顺序将词嵌入输入RNN:h ⃗ 1 , h ⃗ 2 , … , h ⃗ T \vec{h}_1, \vec{h}_2, \ldots, \vec{h}_T h 1 , h 2 , … , h T 在每个时刻,用当前隐藏状态h ⃗ t \vec{h}_t h t y ⃗ ^ t = softmax ( U h ⃗ t ) \hat{\vec{y}}_t = \text{softmax}(U \vec{h}_t) y ^ t = softmax ( U h t ) 计算交叉熵损失:L t = − log y ^ t , w t + 1 \mathcal{L}_t = -\log \hat{y}_{t, w_{t+1}} L t = − log y ^ t , w t + 1 w t + 1 w_{t+1} w t + 1 T
L t
=
− T 1 t = 1 ∑ T log P ( w t + 1 ∣ w 1 , … , w t )
,
…
,
w t
E
下一时刻的隐藏状态h ⃗ t + 1 \vec{h}_{t+1} h t + 1 W h h W_{hh} W hh t
∂ L
=
1
∂ L
=
t + 1
梯度消失(Vanishing Gradient)
梯度爆炸(Exploding Gradient)
0.8 10 ≈ 0.11 0.8^{10} \approx 0.11 0. 8 10 ≈ 0.11 0.8 50 ≈ 0.000014 0.8^{50} \approx 0.000014 0. 8 50 ≈ 0.000014 num_layers: RNN层数(堆叠多层RNN)
"""
super (RNNLanguageModel, self ). __init__ ()
self .hidden_size = hidden_size
self .num_layers = num_layers
# 词嵌入层:将词ID转换为稠密向量
self .embedding = nn.Embedding(vocab_size, embed_size)
# RNN层:PyTorch提供了高效实现
self .rnn = nn.RNN(
input_size = embed_size,
hidden_size = hidden_size,
num_layers = num_layers,
batch_first = True , # 输入形状为(batch, seq, feature)
dropout = 0.3 if num_layers > 1 else 0 # 多层时使用dropout
)
# 输出层:隐藏状态映射到词表上的概率分布
self .fc = nn.Linear(hidden_size, vocab_size)
def forward (self, x, hidden = None ):
"""
前向传播
Args:
x: (batch_size, seq_len) 输入词序列的ID
hidden: (num_layers, batch_size, hidden_size) 初始隐藏状态
如果为None,会初始化为全0
Returns:
output: (batch_size, seq_len, vocab_size) 每个位置的词概率分布
hidden: (num_layers, batch_size, hidden_size) 最终隐藏状态
"""
batch_size, seq_len = x.shape
# 步骤1:词嵌入
embeds = self .embedding(x) # (batch, seq_len, embed_size)
# 步骤2:通过RNN
# rnn_out包含所有时刻的隐藏状态
# hidden是最后时刻的隐藏状态(可以传递给下一个batch)
rnn_out, hidden = self .rnn(embeds, hidden)
# rnn_out: (batch, seq_len, hidden_size)
# hidden: (num_layers, batch, hidden_size)
# 步骤3:输出投影
# 将隐藏状态映射到词表大小的logits
output = self .fc(rnn_out) # (batch, seq_len, vocab_size)
return output, hidden
def init_hidden (self, batch_size, device = 'cpu' ):
"""初始化隐藏状态为全0"""
return torch.zeros( self .num_layers, batch_size, self .hidden_size, device = device)
def train_language_model (model, train_data, epochs = 10 , batch_size = 32 , seq_len = 35 , lr = 0.001 ):
"""
训练RNN语言模型
Args:
model: RNN语言模型
train_data: 训练数据(词ID序列)
epochs: 训练轮数
batch_size: 批大小
seq_len: 序列长度(截断BPTT的长度)
lr: 学习率
"""
device = torch.device( 'cuda' if torch.cuda.is_available() else 'cpu' )
model = model.to(device)
optimizer = torch.optim.Adam(model.parameters(), lr = lr)
criterion = nn.CrossEntropyLoss()
# 训练数据预处理:分成批次
num_batches = len (train_data) // (batch_size * seq_len)
train_data = train_data[:num_batches * batch_size * seq_len]
train_data = train_data.reshape(batch_size, - 1 ) # (batch_size, total_seq_len)
for epoch in range (epochs):
model.train()
total_loss = 0
hidden = model.init_hidden(batch_size, device)
# 遍历所有序列片段
for i in range ( 0 , train_data.size( 1 ) - seq_len, seq_len):
# 获取输入和目标
inputs = train_data[:, i:i + seq_len].to(device)
targets = train_data[:, i + 1 :i + seq_len + 1 ].to(device)
# 前向传播
outputs, hidden = model(inputs, hidden)
# outputs: (batch, seq_len, vocab_size)
# targets: (batch, seq_len)
# 计算损失
# 需要reshape以匹配CrossEntropyLoss的输入格式
loss = criterion(
outputs.reshape( - 1 , outputs.size( 2 )), # (batch*seq_len, vocab_size)
targets.reshape( - 1 ) # (batch*seq_len,)
)
# 反向传播
optimizer.zero_grad()
hidden = hidden.detach() # 截断梯度流,实现截断BPTT
loss.backward()
# 梯度裁剪(防止梯度爆炸)
torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm = 5.0 )
optimizer.step()
total_loss += loss.item()
# 计算困惑度
avg_loss = total_loss / (train_data.size( 1 ) // seq_len)
perplexity = torch.exp(torch.tensor(avg_loss))
print ( f "Epoch { epoch + 1} / { epochs } " )
print ( f " Loss: { avg_loss :.4f } " )
print ( f " Perplexity: { perplexity :.2f } " )
def generate_text (model, start_words, word_to_idx, idx_to_word, max_len = 100 , temperature = 1.0 ):
"""
使用训练好的模型生成文本
Args:
model: 训练好的RNN语言模型
start_words: 起始词列表(如["我", "爱"])
word_to_idx: 词到索引的映射
idx_to_word: 索引到词的映射
max_len: 最大生成长度
temperature: 温度参数(控制随机性,>1更随机,<1更确定)
Returns:
生成的文本字符串
"""
device = next (model.parameters()).device
model.eval()
# 将起始词转换为索引
input_ids = [word_to_idx.get(w, word_to_idx[ '<unk>' ]) for w in start_words]
input_tensor = torch.LongTensor([input_ids]).to(device)
# 初始化隐藏状态
hidden = model.init_hidden( 1 , device)
generated_words = start_words.copy()
with torch.no_grad():
# 处理起始词序列,更新hidden state
if len (start_words) > 0 :
_, hidden = model(input_tensor, hidden)
current_input = input_tensor[:, - 1 :] # 最后一个词
# 逐词生成
for _ in range (max_len):
# 预测下一个词
output, hidden = model(current_input, hidden)
# output: (1, 1, vocab_size)
# 应用温度并计算概率
logits = output[ 0 , - 1 ] / temperature
probs = F.softmax(logits, dim = 0 )
# 采样下一个词
next_idx = torch.multinomial(probs, 1 ).item()
next_word = idx_to_word[next_idx]
# 停止条件
if next_word == '<eos>' :
break
generated_words.append(next_word)
# 更新输入
current_input = torch.LongTensor([[next_idx]]).to(device)
return ' ' .join(generated_words)
# 使用示例
if __name__ == "__main__" :
# 假设我们有词表和数据
vocab_size = 10000
# 创建模型
model = RNNLanguageModel(
vocab_size = vocab_size,
embed_size = 256 ,
hidden_size = 512 ,
num_layers = 2
)
print ( f "模型参数量: {sum (p.numel() for p in model.parameters()) :, } " )
# 训练模型(需要真实数据)
# train_language_model(model, train_data)
# 生成文本(需要词表映射)
# text = generate_text(model, ["我", "爱"], word_to_idx, idx_to_word)
# print(text)
T
1
t = 1 ∑ T
log
P
(
w t
∣
w < t
)
)
t
t + 1
t + 1