Transformer自注意力与生成模型 - Attention Is All You Need | 自在学
Transformer自注意力与生成模型
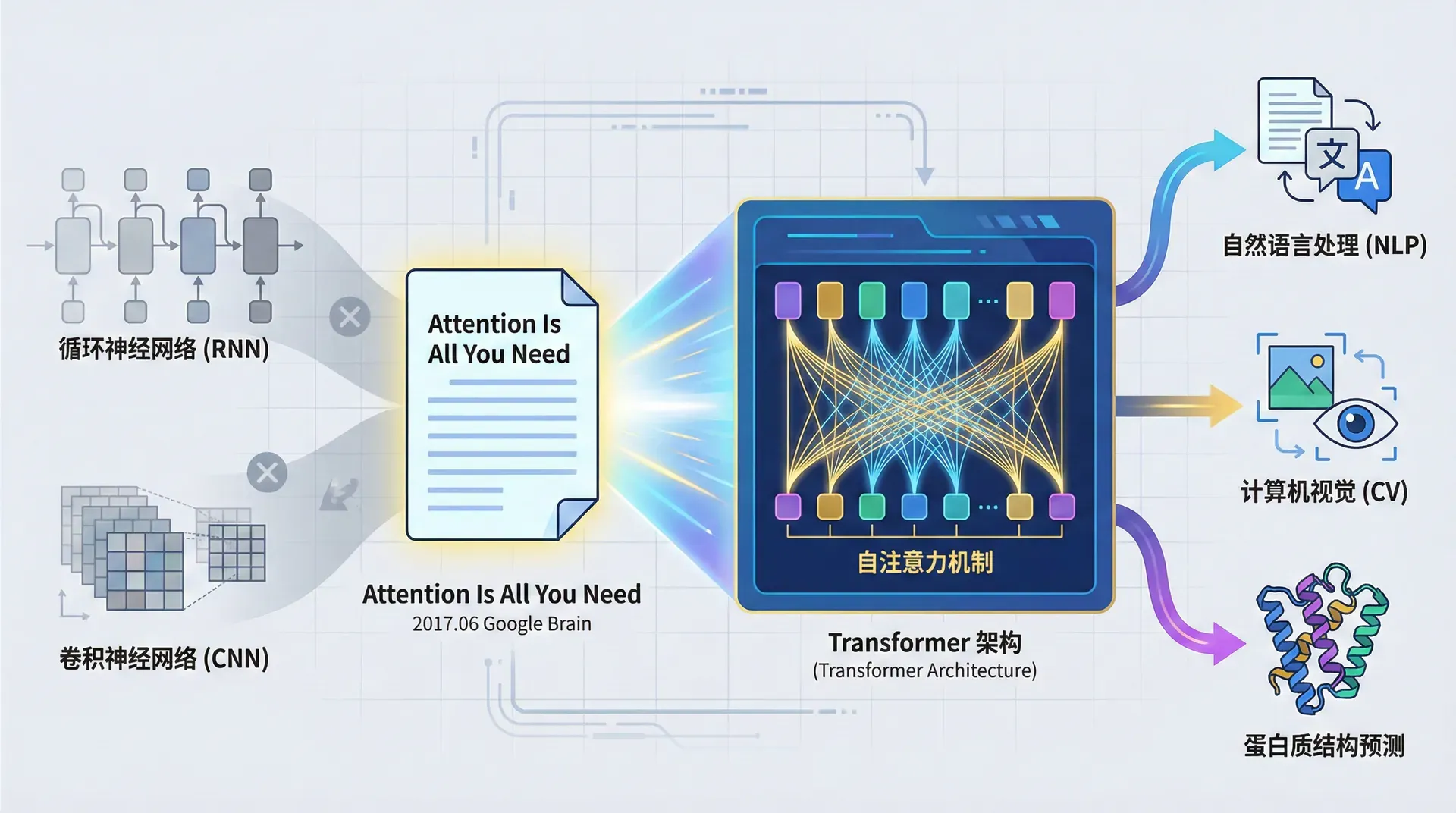
2017年6月,Google Brain团队在arXiv上发表了一篇题为“Attention Is All You Need”的论文。这个看似傲慢的标题实际上概括了一个大胆的主张:我们可以抛弃循环神经网络和卷积神经网络,仅仅用注意力机制就能构建出更强大的序列模型。
五年后回头看,这篇论文开启了一个新纪元——Transformer架构不仅主导了NLP,还在计算机视觉、蛋白质结构预测等领域展现出惊人的威力。
要理解Transformer的革命性,我们需要先回到2017年的NLP现场,理解当时研究者们面临的困境。
在2017年之前,循环神经网络(RNN)及其变体LSTM和GRU是序列建模的标准工具。从机器翻译到文本生成,从语音识别到视频理解,RNN无处不在。然而,随着数据规模和序列长度的增加,RNN的局限性变得越来越明显。
第一个瓶颈是顺序计算的本质 。RNN处理序列的方式是固有顺序的:要计算第10个词的隐藏状态,必须先计算前9个词的隐藏状态。这就像一条流水线,必须等前一个工件完成才能处理下一个。在单核CPU时代,这不是问题;但在GPU并行计算时代,这成了致命的效率障碍。
想象你要翻译一个包含50个词的句子。RNN需要进行50次顺序计算,每一步都依赖前一步的结果。即使你有一块拥有5000个核心的GPU,也无法并行化这50步计算。这意味着训练时间随序列长度线性增长,而且无法充分利用现代硬件的并行能力。
第二个瓶颈是长距离依赖问题 。虽然LSTM通过门控机制缓解了梯度消失,但信息仍然需要逐步传递。考虑这个英文句子:“The keys to the cabinet, which had been lost for decades and finally found by the new owner, are on the table.” 主语“keys”和谓语“are”之间隔了20多个词。RNN需要将“keys”的信息通过20多个时间步传递到“are”,每经过一步,信息都会有所衰减或变形。
实验研究表明,LSTM的有效记忆长度大约在100-200个词之间。对于需要理解整篇文档或长对话历史的任务,这是不够的。更严重的是,即使理论上LSTM可以记住任意长的依赖,在实践中,由于优化困难,它也很难学会利用很远的信息。
第三个瓶颈是计算图的深度 。在反向传播时,梯度需要从输出沿着时间步反向流动到输入。对于长度为n n n n n n
卷积的尝试与局限
面对RNN的困境,研究者们尝试了卷积神经网络(CNN)。卷积天然支持并行计算,而且在计算机视觉中极其成功,为什么不用在NLP上?
2016-2017年,Facebook AI Research提出了一系列基于卷积的序列模型,如ConvS2S(Convolutional Sequence to Sequence)和ByteNet。这些模型确实实现了并行化,训练速度比RNN快得多。然而,卷积有其自身的局限:它的感受野是局部的。
一个卷积核可能只能看到3-5个相邻的词。要捕获长距离依赖,需要堆叠多层卷积,让感受野逐层扩大。但这又带来了新问题:连接两个距离为n n n O ( log n ) O(\log n) O ( log n ) O ( n ) O(n) O ( n )
Transformer的核心洞察极其简单却强大:如果我们希望序列中的任意两个位置能够直接交互,为什么不让它们真的直接交互?
不需要通过中间步骤传递信息(RNN的方式),也不需要堆叠多层来扩大感受野(CNN的方式)。只需要让每个位置直接看到“所有其他位置”,计算它们之间的关联,然后基于这些关联来更新自己的表示。这就是**自注意力(Self-Attention)**的思想。
自注意力实现了三个目标:
常数路径长度 :任意两个位置之间的路径长度都是1,信息可以直接传递,无需经过中间步骤完全并行化 :所有位置的注意力可以同时计算,没有顺序依赖动态权重 :不同位置对当前位置的重要性是动态计算的,而非固定的参数
有了这个核心机制,Vaswani等人构建了一个完全基于注意力的架构,并将其命名为Transformer——它能将输入序列变换(transform)为输出序列,而无需任何循环或卷积。
自注意力机制
自注意力是Transformer的灵魂。虽然注意力机制在Transformer之前就存在(我们在之前学习了seq2seq中的注意力),但Transformer将其系统化并作为唯一的序列建模机制,这是前所未有的。
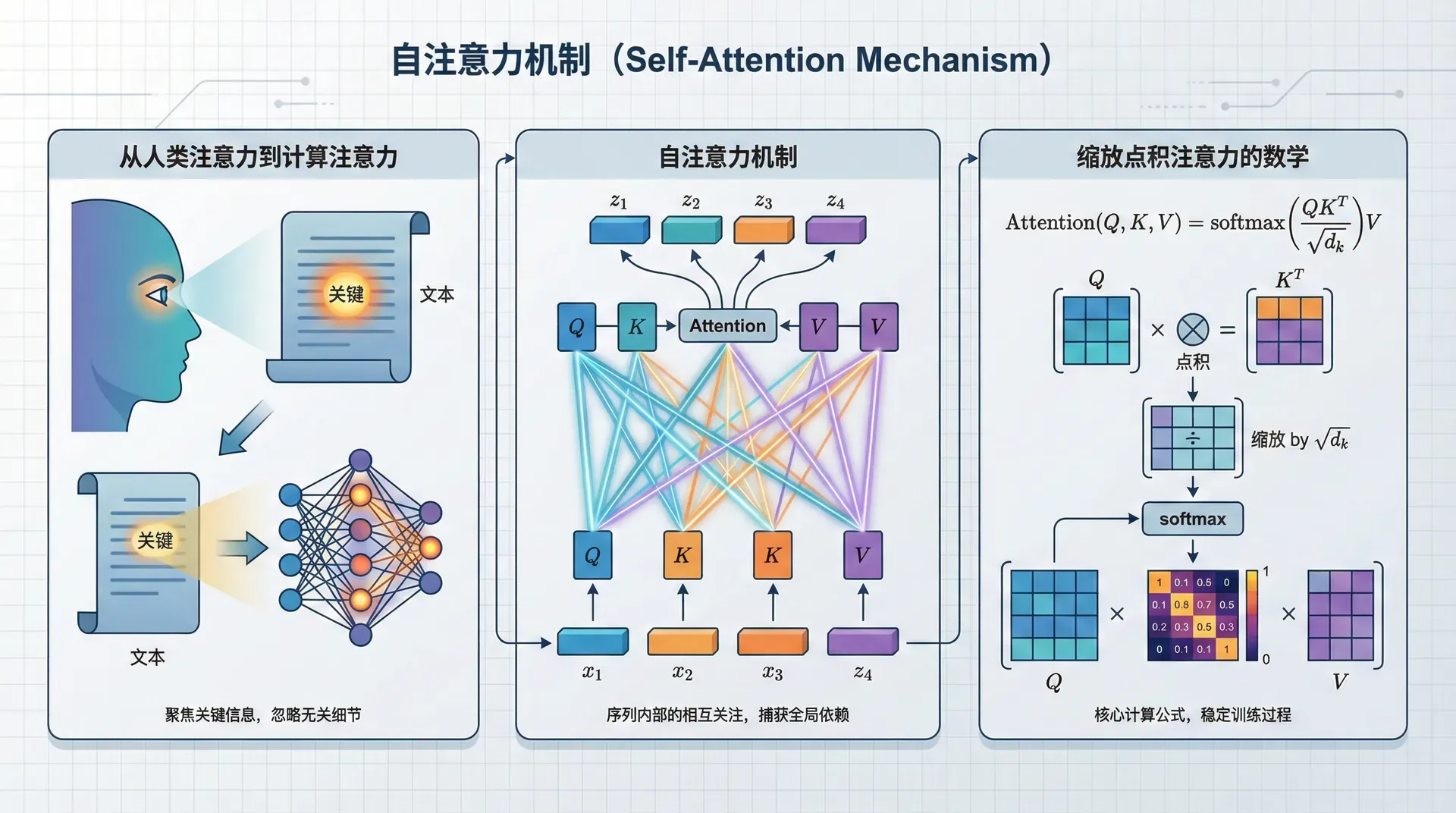
从人类注意力到计算注意力
让我们从一个认知角度理解注意力。当你阅读句子“The animal didn't cross the street because it was too tired”时,你需要理解“it”指的是什么。你的大脑会自动回顾前文,注意到“animal”和“street”两个候选。然后,你会基于“tired”这个词(疲倦是生物的属性)判断“it”更可能指“animal”。
这个过程包含了三个要素:
Query(查询) :“it”这个词在寻找它的指代对象,可以看作是一个“查询”Keys(键) :前文中的每个词都是潜在的候选,它们提供“键”来匹配查询Values(值) :一旦确定了匹配(比如确定“it”指“animal”),我们就使用“animal”的含义(值)来理解“it”
Transformer的自注意力机制正是这个过程的数学化。对于序列中的每个词,模型学习三组向量:Query、Key和Value。然后,通过Query和Key的匹配来决定应该关注哪些词,最后基于匹配权重对Values进行加权求和。
缩放点积注意力的数学
让我们形式化地定义自注意力。假设输入序列的表示矩阵为 X ∈ R n × d X \in \mathbb{R}^{n \times d} X ∈ R n × d n n n d d d
Q = X W Q , K = X W K , V = X W V Q = XW^Q, \quad K = XW^K, \quad V = XW^V Q = X W Q , K = X W K , V = X W 其中 W Q , W K , W V ∈ R d × d k W^Q, W^K, W^V \in \mathbb{R}^{d \times d_k} W Q , W K , W V ∈ R d × d
接下来,我们计算Query和Key之间的相似度。最自然的方式是点积(dot product):
scores = Q K T \text{scores} = QK^T scores = Q K T 这得到一个 n × n n \times n n × n ( i , j ) (i,j) ( i , j ) i i i j j j i i i j j j
但原始点积有个问题:当维度 d k d_k d k d k d_k d k d k = 512 d_k=512 d k =
因此,Transformer使用了缩放因子 1 d k \frac{1}{\sqrt{d_k}} d k 1
scores = Q K T d k \text{scores} = \frac{QK^T}{\sqrt{d_k}} scores = d k 这个缩放将点积的方差控制在1左右,使得softmax的输入保持在一个合理的范围。这看似技术细节,实际上对训练稳定性至关重要。
对这些分数应用softmax,我们得到归一化的注意力权重:
Attention weights = softmax ( Q K T d k ) \text{Attention weights} = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right) Attention weights = softmax ( d k Softmax确保每一行的权重和为1,可以解释为概率分布:位置 i i i j j j
最后,我们用这些权重对Value进行加权求和:
Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V Attention ( Q , K , V ) = softmax ( d k 输出是一个 n × d k n \times d_k n × d k
一个具体的例子
让我们用一个简单的例子来直观理解这个过程。考虑句子"The black cat sat on the mat"(那只黑猫坐在垫子上)。假设我们关注"cat"这个词,想要计算它的自注意力输出。
首先,通过权重矩阵,我们为"cat"生成一个Query向量,为句子中所有词生成Key向量。Query向量可以理解为"cat想要找什么信息",Key向量可以理解为每个词"能提供什么信息"。
然后,我们计算"cat"的Query与每个词的Key的点积(相似度):
"The":分数 0.1
"black":分数 0.7(形容词修饰名词,高相关性)
"cat":分数 0.6(自己关注自己)
"sat":分数 0.3(动词的主语,中等相关性)
"on":分数 0.05
"the":分数 0.05
"mat":分数 0.1
经过softmax归一化,这些分数变成概率分布,假设为:
[0.05, 0.30, 0.25, 0.15, 0.05, 0.05, 0.10]
这意味着在理解"cat"时,模型认为应该重点关注"black"(30%)和"cat"自己(25%),其次关注"sat"(15%)。这符合语言学直觉:"cat"的含义受其修饰词"black"强烈影响,也与它执行的动作"sat"相关。
最后,我们用这些权重对所有词的Value向量进行加权求和:
output cat = 0.05 ⋅ v The + 0.30 ⋅ v black + 0.25 ⋅ v cat + 0.15 ⋅ v sat + … \text{output}_{\text{cat}} = 0.05 \cdot v_{\text{The}} + 0.30 \cdot v_{\text{black}} + 0.25 \cdot v_{\text{cat}} + 0.15 \cdot v_{\text{sat}} + \ldots output cat = 0.05 ⋅ v The + 0.30 ⋅ 结果是"cat"的新表示,它融合了上下文信息,特别是受"black"和"sat"的影响。
自注意力性质
自注意力机制有几个非常美妙的性质:
排列不变性与位置信息 。纯粹的自注意力是排列不变的——如果打乱输入序列的顺序,只是注意力矩阵的行和列被打乱,但计算方式不变。这意味着自注意力本身不编码位置信息。这看似是缺点,实际上是优点:模型不对位置做任何假设,完全从数据中学习位置的重要性。为了提供位置信息,Transformer显式地添加位置编码(我们稍后会讨论),这种设计让位置信息和语义信息解耦。动态性 。与卷积的固定权重不同,自注意力的权重是动态计算的,取决于输入内容。在句子“I went to the bank to deposit money”中,“bank”会强烈关注“deposit money”;而在“I went to the river bank to fish”中,“bank”会强烈关注“river”和“fish”。同样是“bank”,注意力模式完全不同。可解释性 。注意力权重矩阵可以可视化,我们可以直观地看到模型在处理每个词时关注了哪些其他词。这为理解模型的内部工作机制提供了窗口,在很多研究中帮助发现了模型学到的语言现象(如句法树结构、指代关系等)。计算复杂度 。自注意力的时间复杂度是 O ( n 2 d ) O(n^2d) O ( n 2 d ) O ( n 2 ) O(n^2) O ( n 2 )
多头注意力
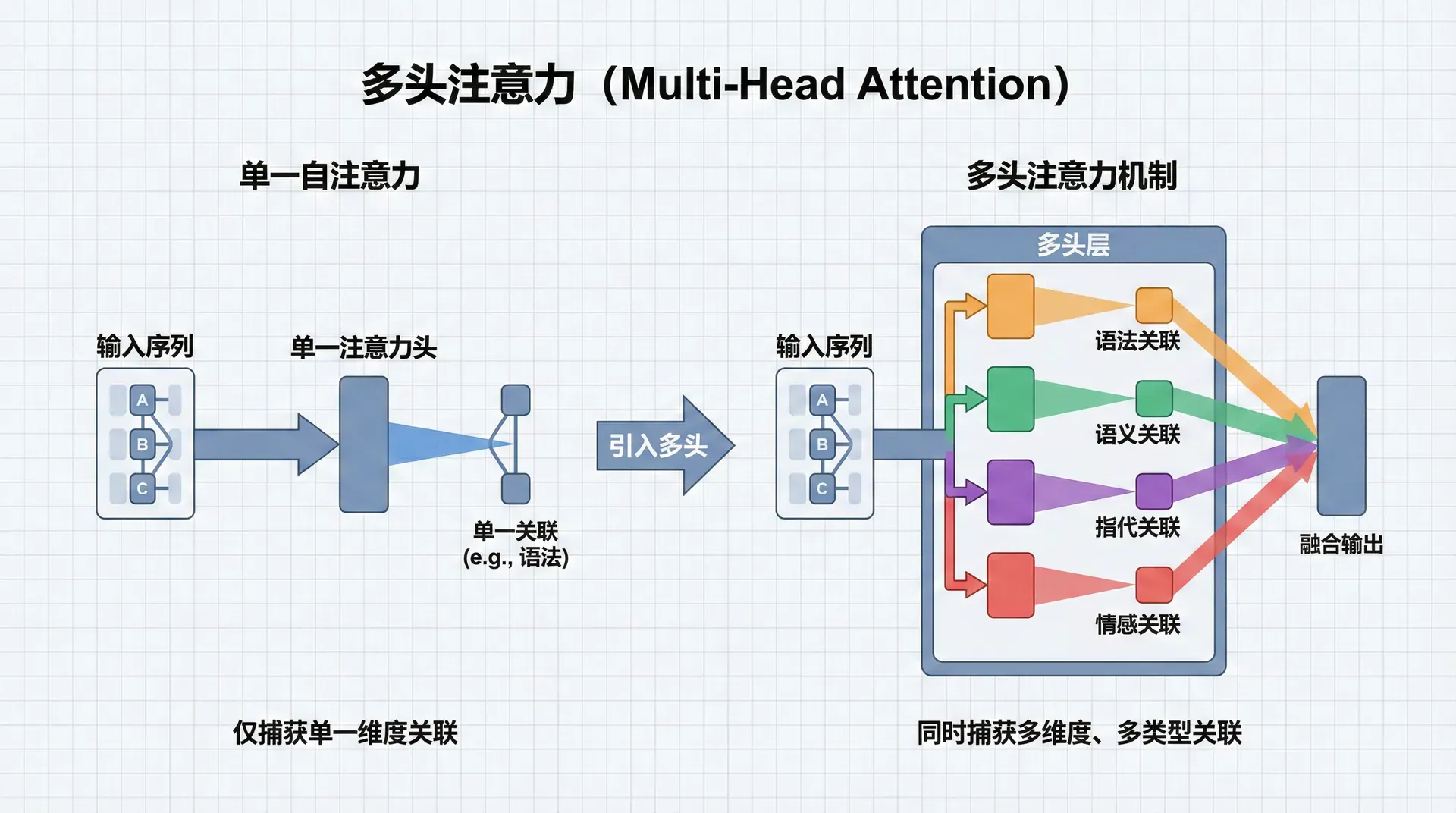
单一的自注意力层可以捕获词与词之间的关联,但这种关联是一维的、单一的。然而,语言中的关联是多方面的:有语法关联(主谓、动宾)、语义关联(同义、反义)、指代关联(代词-先行词)、情感关联等。为了让模型能够同时捕获这些不同类型的关联,Transformer引入了多头注意力(Multi-Head Attention) 。
多视角的直观理解
多头注意力的思想可以类比为多位专家的会诊。单头注意力就像请一位医生诊断,他会从他的专业角度给出判断。多头注意力则是请多位不同专科的医生(比如内科、外科、影像科)同时诊断,每位医生从自己的角度关注不同的症状和指标,最后综合所有医生的意见形成诊断结果。
在NLP中,不同的“头”可能学会关注不同的语言现象。例如:
头1可能专注于句法关系,为每个名词找到它对应的动词
头2可能专注于指代关系,为代词找到它的先行词
头3可能专注于语义关联,为一个词找到它的同义词或近义词
头4可能专注于局部上下文,主要关注相邻的词
这种分工不是人为设计的,而是模型在训练过程中自动学会的。不同的头会自发地分化出不同的注意力模式。
多头注意力的实现
形式化地,多头注意力首先将输入通过 h h h h h h
Q i = X W i Q , K i = X W i K , V i = X W i V , i = 1 , … , h Q_i = XW_i^Q, \quad K_i = XW_i^K, \quad V_i = XW_i^V, \quad i = 1, \ldots, h Q i = X W i Q , K 每组投影矩阵的维度是 W i Q , W i K , W i V ∈ R d m o d e l × d k W_i^Q, W_i^K, W_i^V \in \mathbb{R}^{d_{model} \times d_k} W i Q , W i K , W i
然后,在每组Query、Key、Value上独立地计算注意力:
head i = Attention ( Q i , K i , V i ) = softmax ( Q i K i T d k ) V i \text{head}_i = \text{Attention}(Q_i, K_i, V_i) = \text{softmax}\left(\frac{Q_iK_i^T}{\sqrt{d_k}}\right)V_i head i = Attention ( Q i , K i 每个头输出一个 n × d k n \times d_k n × d k
最后,将所有头的输出拼接起来,并通过一个线性变换融合:
MultiHead ( Q , K , V ) = Concat ( head 1 , … , head h ) W O \text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \ldots, \text{head}_h)W^O MultiHead ( Q , K , V ) = Concat ( head 1 , … , head h ) 其中 W O ∈ R h d k × d m o d e l W^O \in \mathbb{R}^{hd_k \times d_{model}} W O ∈ R h d k × d m o d e l
为什么多头有效?
多头注意力的有效性有几个互补的解释:
表达能力 。从表达能力的角度看,多头注意力增加了模型的容量。单头注意力只能学习一种相似度度量(由 W Q W^Q W Q W K W^K W K h h h
注意力多样性 。实验研究表明,不同的头确实会学习到不同的注意力模式。Vig等人(2019)的可视化研究发现,在BERT模型中,有些头主要关注相邻词(捕获局部信息),有些头关注句法父节点(捕获句法结构),有些头关注共指词(捕获指代关系)。这种自发的分工让模型能够同时处理多种语言现象。
集成效应 。从机器学习的角度看,多头注意力类似于集成学习。每个头都是一个"弱学习器",在某些方面表现良好。通过拼接和线性组合,模型可以综合多个头的优势,实现比单头更强的表现。这也解释了为什么增加头数通常能提升性能,直到某个点饱和。
降维的正则化 。每个头使用降维后的表示(d k = d m o d e l / h d_k = d_{model}/h d k = d m o d e l / h
典型的头数选择
在原始Transformer论文中,Vaswani等人使用了 h = 8 h=8 h = 8 d m o d e l = 512 d_{model}=512 d m o d e l = 512 d k = 64 d_k=64 d k
BERT-base:12个头,d m o d e l = 768 d_{model}=768 d m o d e l = 768 d k = 64 d_k=64 d k = 64
BERT-large:16个头,d m o d e l
一个有趣的现象是,头的维度 d k d_k d k
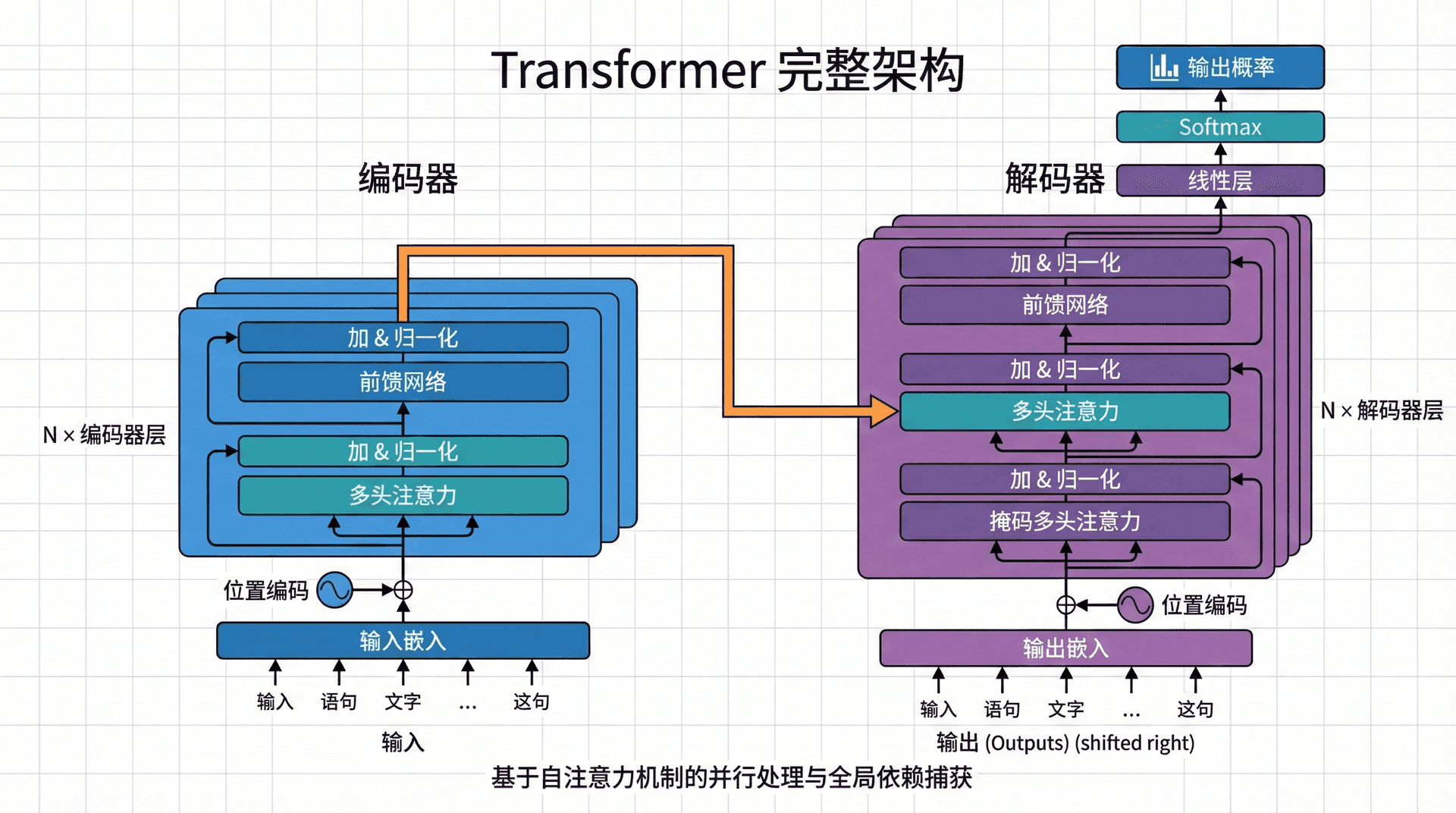
理解了自注意力和多头注意力后,我们现在可以完整地理解Transformer架构。Transformer采用经典的编码器-解码器(Encoder-Decoder)结构,但内部组件完全不同于传统的RNN seq2seq模型。
编码器栈
Transformer的编码器由 N = 6 N=6 N = 6
第一个子层:多头自注意力 。输入序列的每个位置关注序列中的所有位置(包括自己)。这让每个词的表示融合了全局上下文信息。
第二个子层:位置前馈网络(Position-wise Feed-Forward Network) 。这是一个简单但关键的组件,对每个位置独立地应用相同的全连接网络:
FFN ( x ) = max ( 0 , x W 1 + b 1 ) W 2 + b 2 \text{FFN}(x) = \max(0, xW_1 + b_1)W_2 + b_2 FFN ( x ) = max ( 0 , x W 1 + b 1 ) W 这是两个线性变换,中间有ReLU激活。注意"位置独立"(position-wise)的含义:同样的 W 1 , W 2 W_1, W_2 W 1 , W 2
前馈网络的作用是什么?自注意力擅长聚合信息——它将序列中多个位置的信息混合到一起。但自注意力本质上是线性操作(加权求和),缺乏非线性变换能力。前馈网络提供了这种非线性,让模型能够学习更复杂的函数。
在原始Transformer中,前馈网络的隐藏层维度 d f f = 2048 d_{ff}=2048 d ff = 2048 d m o d e l = 512 d_{model}=512 d m o d e l = 512
残差连接与层归一化 。每个子层外面包裹着残差连接和层归一化:
output = LayerNorm ( x + Sublayer ( x ) ) \text{output} = \text{LayerNorm}(x + \text{Sublayer}(x)) output = LayerNorm ( x + Sublayer ( x )) 残差连接将输入直接加到子层的输出上,缓解了深度网络的梯度消失问题,让模型能够堆叠到很深。层归一化则稳定了训练过程,对每个位置的特征进行归一化(均值0,方差1)。
一个技术细节:原论文使用的是"post-LN"(先子层后归一化),但后续研究发现"pre-LN"(先归一化后子层)训练更稳定,已成为标准做法。
解码器栈
解码器同样由 N = 6 N=6 N = 6
第一个子层:掩码多头自注意力 。与编码器的自注意力类似,但有一个关键区别:在生成第 i i i i − 1 i-1 i − 1
mask i j = { 0 if j > i 1 if j ≤ i \text{mask}_{ij} = \begin{cases}
0 & \text{if } j > i \\
1 & \text{if } j \leq i
\end{cases} mask ij = { 0 1 if j 将掩码为0的位置的注意力分数设为 − ∞ -\infty − ∞
第二个子层:编码器-解码器注意力 (也称交叉注意力)。这个子层让解码器关注编码器的输出。具体地,Query来自解码器当前层的输出,Key和Value来自编码器的最终输出:
CrossAttention ( Q dec , K enc , V enc ) \text{CrossAttention}(Q_{\text{dec}}, K_{\text{enc}}, V_{\text{enc}}) CrossAttention ( Q dec , K enc , V enc ) 这个机制在机器翻译中尤其重要:解码器在生成目标语言的每个词时,可以关注源语言句子的不同部分。例如,在翻译"The black cat"为中文"黑色的猫"时,生成"黑色"时关注"black",生成"猫"时关注"cat"。
第三个子层:位置前馈网络 。与编码器相同的结构。
三个子层都有残差连接和层归一化包裹。
位置编码:注入顺序信息
自注意力本身不编码位置信息——交换句子中两个词的位置,注意力计算的结果(忽略索引顺序)不变。但语言是有顺序的:"狗咬人"和"人咬狗"含义截然不同。为了让模型感知位置,Transformer在输入嵌入上加入位置编码。
Vaswani等人使用了正弦位置编码 ,这是一个精巧的设计:
P E ( p o s , 2 i ) = sin ( p o s 10000 2 i / d m o d e l ) PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d_{model}}}\right) P E ( p os , 2 i ) = sin ( 1000 0 P E ( p o s , 2 i + 1 ) = cos ( p o s 10000 2 i / d m o d e l ) PE_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{model}}}\right) P E ( p os , 2 i + 1 ) = cos ( 1000 0 其中 p o s pos p os n − 1 n-1 n − 1 i i i d m o d e l / 2 − 1 d_{model}/2-1 d m o d e l /2 −
这个设计有几个优美的性质:
确定性 。位置编码是固定的函数,不需要学习参数。这减少了模型的参数量,并且对训练中未见过的位置(如超长序列)也能生成合理的编码。
相对位置信息 。对于位置差为 k k k p o s pos p os p o s + k pos+k p os + k
不同频率 。不同维度使用不同频率的正弦/余弦函数。低维度使用高频率(快速变化),捕获局部位置差异;高维度使用低频率(缓慢变化),捕获全局位置模式。
也有研究尝试使用可学习的位置编码(如BERT中的做法),但实验表明两种方法性能相近。正弦编码的优势在于其外推能力和明确的数学性质。
训练过程
Transformer的训练采用标准的教师强制(Teacher Forcing)策略。在机器翻译中,给定源语言句子和目标语言句子,模型的训练目标是:
L = − ∑ t = 1 T log P ( y t ∣ y < t , x ) \mathcal{L} = -\sum_{t=1}^T \log P(y_t | y_{<t}, x) L = − t = 1 ∑ T log P ( y t ∣ y 其中 x x x y y y
并行化的优势 在训练阶段体现得淋漓尽致。对于长度为n n n n n n n n n
推理过程
推理(生成)时,解码器必须自回归地生成序列:先生成第1个词,然后基于第1个词生成第2个词,以此类推。这个过程是顺序的,无法并行化。
贪婪解码 是最简单的策略:每步选择概率最高的词。但这可能导致次优解——局部最优不等于全局最优。
束搜索(Beam Search) 是常用的策略:维护k k k k k k
推理过程中的一个技术细节是KV缓存(KV Cache) 。在生成第t t t t − 1 t-1 t − 1 O ( n 2 ) O(n^2) O ( n 2 ) O ( n ) O(n) O ( n )
理论理解后,让我们通过代码来加深理解。下面的实现是一个完整但简化的Transformer,适合学习使用。
import torch import torch.nn as nn import torch.nn.functional as F import math
class MultiHeadAttention ( nn . Module ): """多头自注意力机制""" def __init__ (self, d_model, num_heads, dropout = 0.1 ): super (). __init__ () assert d_model % num_heads == 0 这个实现包含了Transformer的所有核心组件,代码可以直接运行。在实际应用中,还需要添加训练循环、学习率调度、标签平滑等技术细节,但核心架构就是这样。
在Transformer的原始论文发表后不久,OpenAI团队意识到Transformer的解码器本身就是一个强大的语言模型。2018年6月,他们发表了GPT(Generative Pre-trained Transformer)论文,标志着生成式预训练时代的开启。
架构简化
GPT采用了仅解码器 的架构,去掉了编码器和编码器-解码器注意力层。模型结构简化为:
词嵌入 + 位置编码
多层掩码自注意力 + 前馈网络(Transformer解码器层,但没有交叉注意力)
输出层
这个设计的动机很简单:对于语言建模任务,我们只需要根据前文预测下一个词,不需要编码器。掩码自注意力确保了自回归性质——每个词只能看到它之前的词。
预训练目标
GPT的预训练目标是标准的语言建模:
L LM = ∑ i log P ( w i ∣ w 1 , … , w i − 1 ; Θ ) \mathcal{L}_{\text{LM}} = \sum_{i} \log P(w_i | w_1, \ldots, w_{i-1}; \Theta) L LM = i ∑ log P ( w 在大规模文本语料(BooksCorpus,8亿词)上训练后,模型学会了预测下一个词。这看似简单的任务实则要求模型理解语法、语义、常识等各方面的语言知识。
GPT的突破在于证明了:预训练语言模型+微调,可以在多个NLP任务上达到当时的最佳或接近最佳性能。这与ELMo同时出现,共同奠定了预训练-微调范式的基础。
从GPT到GPT-3的演进
GPT系列的演进是一个规模扩张的故事:
GPT(2018) :117M参数,12层,在多个任务上验证了预训练-微调的有效性。
GPT-2(2019) :1.5B参数,48层。OpenAI发现,足够大的模型在预训练后,即使不微调,也能通过零样本(zero-shot)方式完成多个任务。这引发了关于模型能力涌现的讨论。
GPT-3(2020) :175B参数,96层。模型展现了惊人的少样本学习(few-shot learning)能力——只需要在prompt中给出几个示例,模型就能完成新任务,无需任何梯度更新。这颠覆了人们对机器学习的认知。
GPT-3的成功证明了两个论点:
规模法则(Scaling Laws) :模型性能随参数量、数据量、计算量的增加而持续提升,且关系可以用幂律拟合涌现能力(Emergent Abilities) :当模型达到某个规模阈值,会突然获得之前没有的能力(如算术推理、代码生成)
NLP的统一架构
Transformer发表后的几年内,几乎所有NLP任务的最佳模型都基于Transformer。从BERT到T5,从XLNet到RoBERTa,每个新模型都是Transformer的某种变体或改进。RNN和CNN在NLP中逐渐被边缘化。
这种统一性带来了巨大的好处。研究者不再需要为每个任务设计特定的架构,而是可以专注于更高层次的问题:如何更好地预训练?如何更有效地微调?如何设计更好的训练目标?这加速了整个领域的进步。
超越NLP的影响
更令人惊讶的是,Transformer的影响远超NLP。在计算机视觉中,Vision Transformer(ViT)证明了Transformer可以完全取代卷积神经网络,在图像分类上达到SOTA。在语音识别、强化学习、蛋白质结构预测等领域,Transformer-based模型都展现出优越性能。
Transformer似乎是一个通用的序列建模架构,或者更广义地说,是一个通用的关系建模架构。自注意力机制让模型能够学习任意元素对之间的关系,而不对这些元素的类型做任何假设。这种通用性是Transformer成功的关键。
改进方向
尽管Transformer取得了巨大成功,它仍有明显的局限性:
计算复杂度 。O ( n 2 ) O(n^2) O ( n 2 )
Sparse Attention (如Longformer):只在局部窗口和部分全局位置计算注意力Linearized Attention (如Performer):通过核技巧将复杂度降到O ( n ) O(n) O ( n ) 低秩近似 (如Linformer):假设注意力矩阵是低秩的,通过投影降维
数据效率 。Transformer缺乏归纳偏置(inductive bias)——它不对数据的结构做任何假设。CNN对图像有平移不变性的偏置,RNN对序列有时间连续性的偏置,而Transformer是“一张白纸”。这使得Transformer需要更多数据才能学好,在低资源场景下可能不如有偏置的模型。
可解释性 。虽然注意力权重可以可视化,但多层多头的Transformer内部发生了什么,仍然很难理解。注意力可视化往往展示出混乱的模式,难以提取清晰的语言学洞察。
Transformer是否是序列建模的终极答案?可能不是。但它提供了一个强大的基线和思想框架。未来的模型可能会:
融合注意力和其他机制(如循环、记忆、检索)
设计更高效的注意力变体
引入适当的归纳偏置以提高数据效率
开发更好的位置编码和结构编码
无论如何,Transformer已经深刻地改变了AI研究的面貌。“Attention Is All You Need”这个标题在2017年看起来像是挑衅,但在2026年回望,它更像是一个预言的实现。
练习与思考
解释为什么缩放点积注意力需要除以d k \sqrt{d_k} d k
比较RNN和Transformer在处理句子"The keys to the cabinet are on the table"时的信息流。为什么Transformer能更好地捕获"keys"和"are"之间的长距离依赖?
为什么要使用多个注意力头,而不是使用一个更大的单头?多头注意力的设计哲学是什么?你能想到什么时候单头可能更好吗?
正弦位置编码使用了不同频率的正弦和余弦函数。这个设计如何帮助模型学习相对位置关系?如果改用可学习的位置嵌入,会有什么优缺点?
计算Transformer编码一个长度为n n n
V
k
512
Q
K T
Q K T
)
Q K T
)
V
v black
+
0.25 ⋅
v cat +
0.15 ⋅
v sat +
…
i
=
X W i K , V i =
X W i V , i =
1 , … , h
V
∈
R d m o d e l × d k
d k = d m o d e l / h d_k = d_{model}/h d k = d m o d e l / h
,
V i
)
=
W O
n × h d k = n × d m o d e l n \times hd_k = n \times d_{model} n × h d k = n × d m o d e l n × d m o d e l n \times d_{model} n × d m o d e l
=
64
= 1024 d_{model}=1024 d m o d e l = 1024
GPT-3:96个头,d m o d e l = 12288 d_{model}=12288 d m o d e l = 12288 d k = 128 d_k=128 d k = 128
2
+
b 2
>
i
if j ≤ i
2 i / d m o d e l
p os
)
2 i / d m o d e l
p os
)
1
< t
,
x
)
,
"d_model must be divisible by num_heads"
self .d_model = d_model
self .num_heads = num_heads
self .d_k = d_model // num_heads # 每个头的维度
# Q, K, V的线性投影
self .W_q = nn.Linear(d_model, d_model)
self .W_k = nn.Linear(d_model, d_model)
self .W_v = nn.Linear(d_model, d_model)
# 输出投影
self .W_o = nn.Linear(d_model, d_model)
self .dropout = nn.Dropout(dropout)
def scaled_dot_product_attention (self, Q, K, V, mask = None ):
"""
缩放点积注意力
Args:
Q, K, V: (batch, num_heads, seq_len, d_k)
mask: (batch, 1, 1, seq_len) 或 (batch, 1, seq_len, seq_len)
Returns:
output: (batch, num_heads, seq_len, d_k)
attention_weights: (batch, num_heads, seq_len, seq_len)
"""
# 计算注意力分数
scores = torch.matmul(Q, K.transpose( - 2 , - 1 )) / math.sqrt( self .d_k)
# 应用掩码(如果有)
if mask is not None :
scores = scores.masked_fill(mask == 0 , float ( '-inf' ))
# Softmax归一化
attention_weights = F.softmax(scores, dim =- 1 )
attention_weights = self .dropout(attention_weights)
# 加权求和Value
output = torch.matmul(attention_weights, V)
return output, attention_weights
def forward (self, query, key, value, mask = None ):
"""
Args:
query, key, value: (batch, seq_len, d_model)
mask: 注意力掩码
Returns:
output: (batch, seq_len, d_model)
"""
batch_size = query.size( 0 )
# 线性投影并分成多头
# (batch, seq_len, d_model) -> (batch, seq_len, num_heads, d_k) -> (batch, num_heads, seq_len, d_k)
Q = self .W_q(query).view(batch_size, - 1 , self .num_heads, self .d_k).transpose( 1 , 2 )
K = self .W_k(key).view(batch_size, - 1 , self .num_heads, self .d_k).transpose( 1 , 2 )
V = self .W_v(value).view(batch_size, - 1 , self .num_heads, self .d_k).transpose( 1 , 2 )
# 计算注意力
attn_output, self .attention_weights = self .scaled_dot_product_attention(Q, K, V, mask)
# 拼接多头
# (batch, num_heads, seq_len, d_k) -> (batch, seq_len, num_heads, d_k) -> (batch, seq_len, d_model)
attn_output = attn_output.transpose( 1 , 2 ).contiguous().view(batch_size, - 1 , self .d_model)
# 输出投影
output = self .W_o(attn_output)
return output
class PositionwiseFeedForward ( nn . Module ):
"""位置前馈网络"""
def __init__ (self, d_model, d_ff, dropout = 0.1 ):
super (). __init__ ()
self .linear1 = nn.Linear(d_model, d_ff)
self .linear2 = nn.Linear(d_ff, d_model)
self .dropout = nn.Dropout(dropout)
def forward (self, x):
# FFN(x) = max(0, xW1 + b1)W2 + b2
return self .linear2( self .dropout(F.relu( self .linear1(x))))
class EncoderLayer ( nn . Module ):
"""Transformer编码器层"""
def __init__ (self, d_model, num_heads, d_ff, dropout = 0.1 ):
super (). __init__ ()
self .self_attn = MultiHeadAttention(d_model, num_heads, dropout)
self .feed_forward = PositionwiseFeedForward(d_model, d_ff, dropout)
self .norm1 = nn.LayerNorm(d_model)
self .norm2 = nn.LayerNorm(d_model)
self .dropout1 = nn.Dropout(dropout)
self .dropout2 = nn.Dropout(dropout)
def forward (self, x, mask = None ):
"""
Args:
x: (batch, seq_len, d_model)
mask: 注意力掩码
Returns:
output: (batch, seq_len, d_model)
"""
# 子层1:多头自注意力 + 残差连接 + 层归一化
attn_output = self .self_attn(x, x, x, mask)
x = self .norm1(x + self .dropout1(attn_output))
# 子层2:前馈网络 + 残差连接 + 层归一化
ff_output = self .feed_forward(x)
x = self .norm2(x + self .dropout2(ff_output))
return x
class DecoderLayer ( nn . Module ):
"""Transformer解码器层"""
def __init__ (self, d_model, num_heads, d_ff, dropout = 0.1 ):
super (). __init__ ()
self .self_attn = MultiHeadAttention(d_model, num_heads, dropout)
self .cross_attn = MultiHeadAttention(d_model, num_heads, dropout)
self .feed_forward = PositionwiseFeedForward(d_model, d_ff, dropout)
self .norm1 = nn.LayerNorm(d_model)
self .norm2 = nn.LayerNorm(d_model)
self .norm3 = nn.LayerNorm(d_model)
self .dropout1 = nn.Dropout(dropout)
self .dropout2 = nn.Dropout(dropout)
self .dropout3 = nn.Dropout(dropout)
def forward (self, x, encoder_output, src_mask = None , tgt_mask = None ):
"""
Args:
x: 解码器输入 (batch, tgt_len, d_model)
encoder_output: 编码器输出 (batch, src_len, d_model)
src_mask: 源序列掩码
tgt_mask: 目标序列掩码(防止看到未来)
Returns:
output: (batch, tgt_len, d_model)
"""
# 子层1:掩码多头自注意力
self_attn_output = self .self_attn(x, x, x, tgt_mask)
x = self .norm1(x + self .dropout1(self_attn_output))
# 子层2:编码器-解码器注意力
cross_attn_output = self .cross_attn(x, encoder_output, encoder_output, src_mask)
x = self .norm2(x + self .dropout2(cross_attn_output))
# 子层3:前馈网络
ff_output = self .feed_forward(x)
x = self .norm3(x + self .dropout3(ff_output))
return x
class PositionalEncoding ( nn . Module ):
"""位置编码"""
def __init__ (self, d_model, max_len = 5000 , dropout = 0.1 ):
super (). __init__ ()
self .dropout = nn.Dropout(dropout)
# 创建位置编码矩阵
pe = torch.zeros(max_len, d_model)
position = torch.arange( 0 , max_len, dtype = torch.float).unsqueeze( 1 )
div_term = torch.exp(torch.arange( 0 , d_model, 2 ).float() * ( - math.log( 10000.0 ) / d_model))
pe[:, 0 :: 2 ] = torch.sin(position * div_term)
pe[:, 1 :: 2 ] = torch.cos(position * div_term)
pe = pe.unsqueeze( 0 ) # (1, max_len, d_model)
self .register_buffer( 'pe' , pe)
def forward (self, x):
"""
Args:
x: (batch, seq_len, d_model)
"""
x = x + self .pe[:, :x.size( 1 )]
return self .dropout(x)
class Transformer ( nn . Module ):
"""完整的Transformer模型"""
def __init__ (self, src_vocab_size, tgt_vocab_size, d_model = 512 , num_heads = 8 ,
num_encoder_layers = 6 , num_decoder_layers = 6 , d_ff = 2048 , dropout = 0.1 , max_len = 5000 ):
super (). __init__ ()
# 嵌入层
self .src_embedding = nn.Embedding(src_vocab_size, d_model)
self .tgt_embedding = nn.Embedding(tgt_vocab_size, d_model)
# 位置编码
self .pos_encoding = PositionalEncoding(d_model, max_len, dropout)
# 编码器
self .encoder_layers = nn.ModuleList([
EncoderLayer(d_model, num_heads, d_ff, dropout)
for _ in range (num_encoder_layers)
])
# 解码器
self .decoder_layers = nn.ModuleList([
DecoderLayer(d_model, num_heads, d_ff, dropout)
for _ in range (num_decoder_layers)
])
# 输出层
self .fc_out = nn.Linear(d_model, tgt_vocab_size)
self .d_model = d_model
self .dropout = nn.Dropout(dropout)
# 初始化参数
self ._reset_parameters()
def _reset_parameters (self):
for p in self .parameters():
if p.dim() > 1 :
nn.init.xavier_uniform_(p)
def encode (self, src, src_mask = None ):
"""编码器前向传播"""
# 嵌入 + 位置编码
x = self .src_embedding(src) * math.sqrt( self .d_model)
x = self .pos_encoding(x)
# 通过编码器层
for layer in self .encoder_layers:
x = layer(x, src_mask)
return x
def decode (self, tgt, encoder_output, src_mask = None , tgt_mask = None ):
"""解码器前向传播"""
# 嵌入 + 位置编码
x = self .tgt_embedding(tgt) * math.sqrt( self .d_model)
x = self .pos_encoding(x)
# 通过解码器层
for layer in self .decoder_layers:
x = layer(x, encoder_output, src_mask, tgt_mask)
return x
def forward (self, src, tgt, src_mask = None , tgt_mask = None ):
"""
Args:
src: 源序列 (batch, src_len)
tgt: 目标序列 (batch, tgt_len)
src_mask: 源序列掩码
tgt_mask: 目标序列掩码
Returns:
output: (batch, tgt_len, tgt_vocab_size)
"""
encoder_output = self .encode(src, src_mask)
decoder_output = self .decode(tgt, encoder_output, src_mask, tgt_mask)
output = self .fc_out(decoder_output)
return output
def create_masks (src, tgt, pad_idx = 0 ):
"""创建掩码"""
# 源序列掩码(隐藏padding)
src_mask = (src != pad_idx).unsqueeze( 1 ).unsqueeze( 2 ) # (batch, 1, 1, src_len)
# 目标序列掩码(隐藏padding + 未来信息)
tgt_len = tgt.size( 1 )
tgt_pad_mask = (tgt != pad_idx).unsqueeze( 1 ).unsqueeze( 2 ) # (batch, 1, 1, tgt_len)
tgt_sub_mask = torch.tril(torch.ones((tgt_len, tgt_len), device = tgt.device)).bool() # (tgt_len, tgt_len)
tgt_mask = tgt_pad_mask & tgt_sub_mask
return src_mask, tgt_mask
# 使用示例
if __name__ == "__main__" :
# 模型参数
src_vocab_size = 10000
tgt_vocab_size = 10000
d_model = 512
num_heads = 8
num_layers = 6
# 创建模型
model = Transformer(src_vocab_size, tgt_vocab_size, d_model, num_heads, num_layers)
# 示例输入
src = torch.randint( 1 , src_vocab_size, ( 2 , 10 )) # (batch=2, src_len=10)
tgt = torch.randint( 1 , tgt_vocab_size, ( 2 , 8 )) # (batch=2, tgt_len=8)
# 创建掩码
src_mask, tgt_mask = create_masks(src, tgt)
# 前向传播
output = model(src, tgt, src_mask, tgt_mask)
print ( f "Output shape: { output.shape } " ) # (2, 8, 10000)
i
∣
w 1
,
…
,
w i − 1
;
Θ
)
d d d
你要为一个客服聊天机器人选择模型架构。对话历史可能很长(几十轮对话),但每轮对话的文本较短(几句话)。你会选择标准Transformer、优化的Transformer变体(如Longformer)、还是混合架构?为什么?
Transformer在NLP和CV中都取得了成功。这是否意味着存在一个“通用的学习架构”?Transformer的成功对构建通用人工智能(AGI)有什么启示?它的局限性又提示了什么?